IDENTIFYING PATTERNS IN SPATIAL DATA Xun Zhou University

IDENTIFYING PATTERNS IN SPATIAL DATA Xun Zhou University of Iowa September 5, 2014

OUTLINE • Introduction • Spatial Data and Models • Statistical models • Spatial Pattern Families • Computational Challenges

WHAT IS SPATIAL DATA MINING (SDM) • Identifying interesting, non-trivia, and useful patterns from large spatial datasets • “Spatial” is general – includes spatio-temporal • Examples of spatial/spatio-temporal datasets: • • GPS traces Facebook / Twitter check-ins Climate observations (e. g. , rainfall, temperature, etc). Remotely sensed images (e. g. , NASA products) Crime reports Disease maps and records Traffic statistics and road networks Sales/market price data, supply maps

WHY IS SDM IMPORTANT • Location/time information brings rich context Support decision making • Understanding natural phenomenon • Improve the quality of knowledge • • London Cholera 1854 – John Snow • Modern examples Predict land cover type with limited samples • Which animals often live in the same area? • Detect outbreaks of diseases/crimes • Find anomalous climate events • Picture Courtesy: Prof. Shashi Shekhar @ UMN

WHAT IS “SPECIAL” ABOUT “SPATIAL” Traditional Data Mining Spatial Data Mining Data Types Age, salary, text… (in addition) Location, shape, time … Relationships Arithmetic, Ordering, Subset… Topological, directional, metric… Statistical models Data follows i. i. d. Data is auto-correlated & heterogeneous Output pattern Diaper + beer = frequent set Diaper + beer only frequent in blue-collar neighborhoods Computation … … Picture Source: [1]

SPATIAL DATA MINING COMPONENTS • Input Data • Statistical Foundations • Output patterns • Computational Process

OUTLINE • Introduction • Spatial Data and Models • Statistical models • Spatial Pattern Families • Computational Challenges

SPATIAL DATA TYPES • Two data representation models Vector Data (Object Model) Raster Data (Field Model) Data representation Geometric objects Continuous field with attribute functions Examples Disease reports (point) GPS traces (lines/curves) Counties, states (polygons) Satellite images Temperature map of the U. S. Vegetation cover in Africa Picture source: [2]

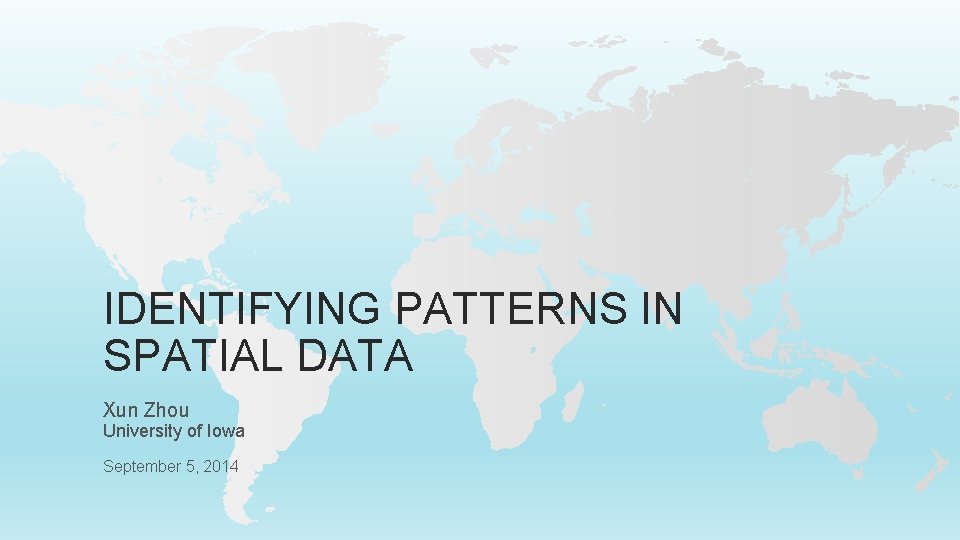
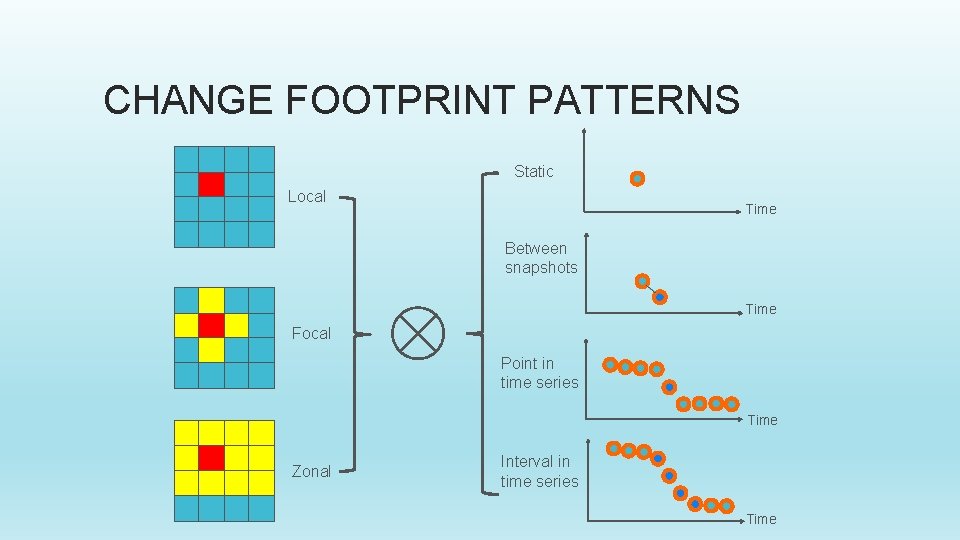
SPATIAL RELATIONSHIPS AND OPERATIONS • Between spatial objects: Set-oriented: Union, Intersection, Membership… • Topological: Meet, within, overlap, connected… • Directional: North, East, left, above, below… • Metric: Distance, area, perimeter • • Spatial field operations • Local, Focal, Zonal, Global Individual location (elevation > 1000 ft. ) A small neighborhood (slope, gradient) Part of a region (Mountain peak) Among all the locations (The Everest)

OUTLINE • Introduction • Spatial Data and Models • Statistical models • Spatial Pattern Families • Computational Challenges

TWO KEY FEATURES • Spatial Autocorrelation The first law of geography[*]: “Everything is related to everything, but near things are more relevant than distant things”. • Spatial features are usually auto-correlated or clustered rather than randomly distributed • • Spatial heterogeneity • Spatial patterns are not uniform globally – they vary from place to place. [*] Tobler W. , (1970) "A computer movie simulating urban growth in the Detroit region". Economic Geography, 46(2): 234 -240.

STATISTICAL FOUNDATIONS • Spatial statistics – a brunch of statistics Models[4] Geostatistical Lattice(Areal) Point Process Scenarios Continuous space Disjoint and complete partitions of the space (e. g. , grids, areas) Distribution of points Examples Temperature in US Population of counties Locations of birds Major techniques Kriging (spatial interpolation) Spatial Autoregressive Regression (SAR) Markov Random Field (MRF) Ripley’s K-function Cross k-function Complete Spatial Randomness (CSR) * These are statistical models (like normal distribution) and may not lineup with data representation models.

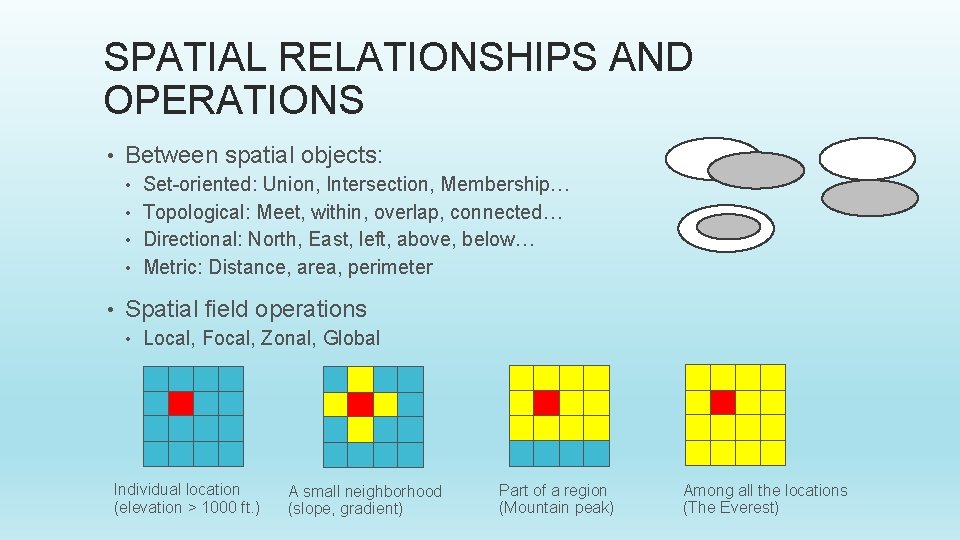
SPATIAL NEIGHBORHOOD • A collection of nearby location/spatial object Adjacent/connected objects/locations • Within a certain distance • r • The W-matrix: A B C D

OUTLINE • Introduction • Spatial Data and Models • Statistical models • Spatial Pattern Families • Computational Challenges

SPATIAL PATTERN FAMILIES • A comparison with traditional DM tasks Traditional Data Mining Pattern Families Spatial Data Mining Pattern Families Prediction/Classification Spatial Prediction/Geographic Classification Clustering Spatial Clustering/Hotspot detection Anomaly Detection Spatial Anomaly/Outlier Detection Association Rule Mining Spatial Co-location Patterns

SPATIAL PREDICTION • C 4. 5 results on land cover data [5] Traditional classifiers based on i. i. d. and global model Linear regression, Decision Tree, SVM, CART, etc. • Spatial auto-correlation and variation are not modeled • • Predicting land cover types, location-based recommendation • Regression Linear regression • SAR GWR Spatial Decision Tree[5] Information gain function: add spatial autocorrelation measure Spatial • Decision rules: Traditional • f(x) > 1? Left : Right Flip if neighbors classified differently Illustration of focal-test-based spatial decision tree[5]

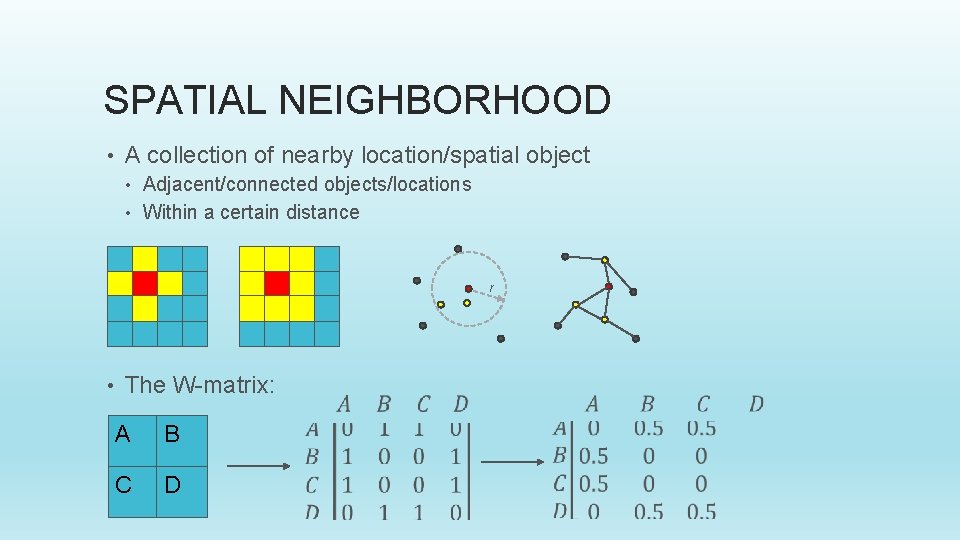
SPATIAL OUTLIER DETECTION • Traditional Anomaly Detection • • Data is anomalous w. r. t. global data distribution Spatial outlier[6] Data is anomalous w. r. t. its neighbors (discontinuity) • Finding Suspicious buildings, broken sensors, or other points of interest… • Methods: • Variogram clouds • Moran scatterplot • Spatial Statistic (S) • 1 1 1 2 4 5 1 1 1 2 4 5 2 2 4 5 4 4 4 5 5 5 5 1 -D spatial data and distribution [1]

SPATIAL ASSOCIATION • Spatial Co-location pattern[7] Given a number of spatial object types and instances • Find sets of types that are frequently located in proximity • Example: {Fox, Rabbits}, {Nile Crocodiles, Egyptian Plover} • Frequent item set Co-location Comment Transactions Neighbor set Space is continuous, no transactions Support, Confidence Participation index PI = min(AB/A, AB/B) {‘+’, ‘x’}, {‘o’, ‘*’} Pictures source: [1]

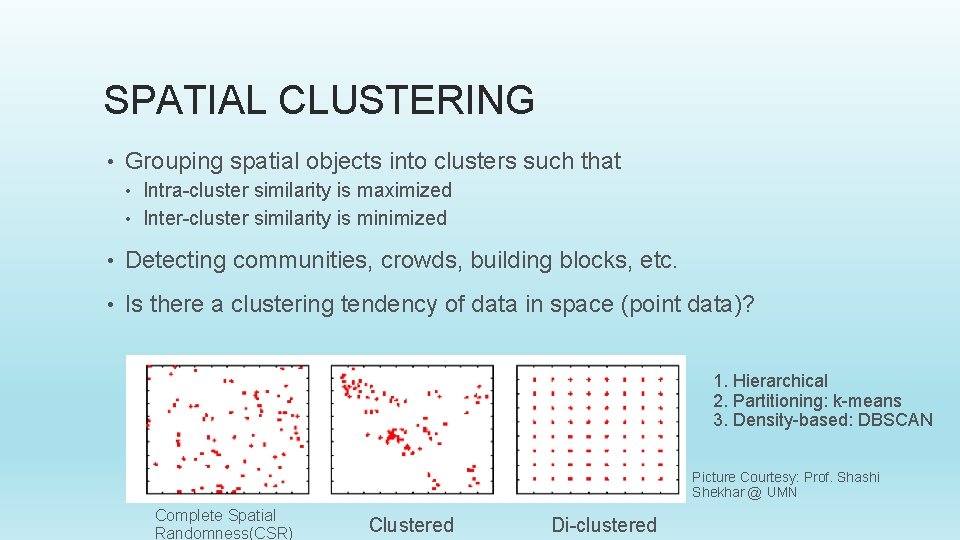
SPATIAL CLUSTERING • Grouping spatial objects into clusters such that Intra-cluster similarity is maximized • Inter-cluster similarity is minimized • • Detecting communities, crowds, building blocks, etc. • Is there a clustering tendency of data in space (point data)? 1. Hierarchical 2. Partitioning: k-means 3. Density-based: DBSCAN Picture Courtesy: Prof. Shashi Shekhar @ UMN Complete Spatial Randomness(CSR) Clustered Di-clustered

SPATIAL HOTSPOT DETECTION • Special case of clustering Identify regions with high density - not a complete partitioning of data • Ignore noise or sparse clusters • Crime/disease outbreaks, traffic jam, water pollution… • Statistical significance – avoid random clusters • • Density-based approaches: DBSCAN[8] • Statistical tests – spatial scan statistics[9] (public health) Spatial Scan Statistics DBSCAN

NEW DIMENSIONS OF SPATIAL PATTERNS • Patterns on Spatial Networks Hotspots (Dangerous routes with high risk of accidents)[10] • Clusters (Crimes along the streets, bus/bike route planning) • Predictions • • Irregular/complex-shaped Spatial Patterns • Complex-shaped clusters (terrain constraints) • Irregular Hotspots (gerrymander …) Results on pedestrian fatality data from Orlando, FL. [10]

ADDING TIME • Input data • Spatial data Spatio-temporal data Time series • Vector: point sequences, polygon series… • Raster: image sequences, spatial time series (a time series at each grid) • • • Relationship: before, after, during, simultaneous, … Statistical Foundations Markov Chain, Hidden Markov Model… • Spatiotemporal Statistics •

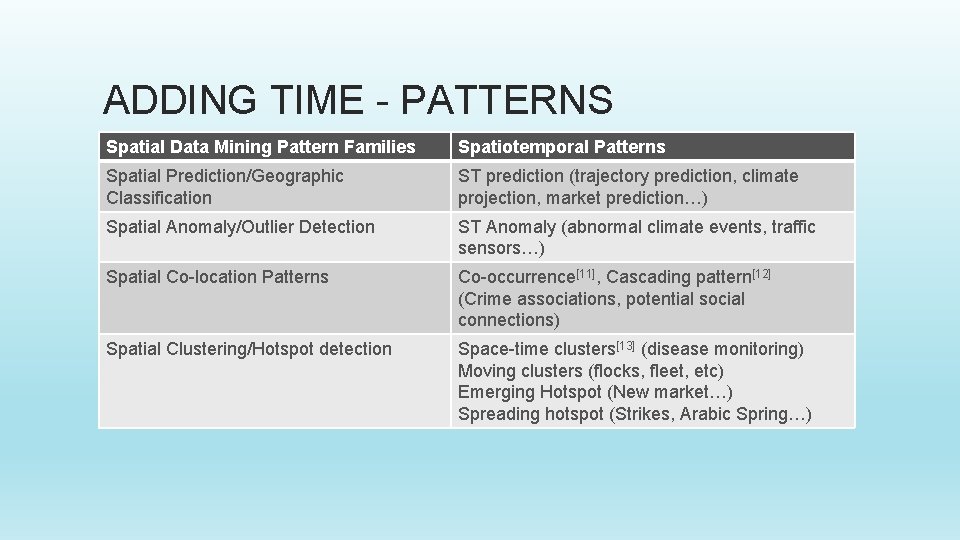
ADDING TIME - PATTERNS Spatial Data Mining Pattern Families Spatiotemporal Patterns Spatial Prediction/Geographic Classification ST prediction (trajectory prediction, climate projection, market prediction…) Spatial Anomaly/Outlier Detection ST Anomaly (abnormal climate events, traffic sensors…) Spatial Co-location Patterns Co-occurrence[11], Cascading pattern[12] (Crime associations, potential social connections) Spatial Clustering/Hotspot detection Space-time clusters[13] (disease monitoring) Moving clusters (flocks, fleet, etc) Emerging Hotspot (New market…) Spreading hotspot (Strikes, Arabic Spring…)

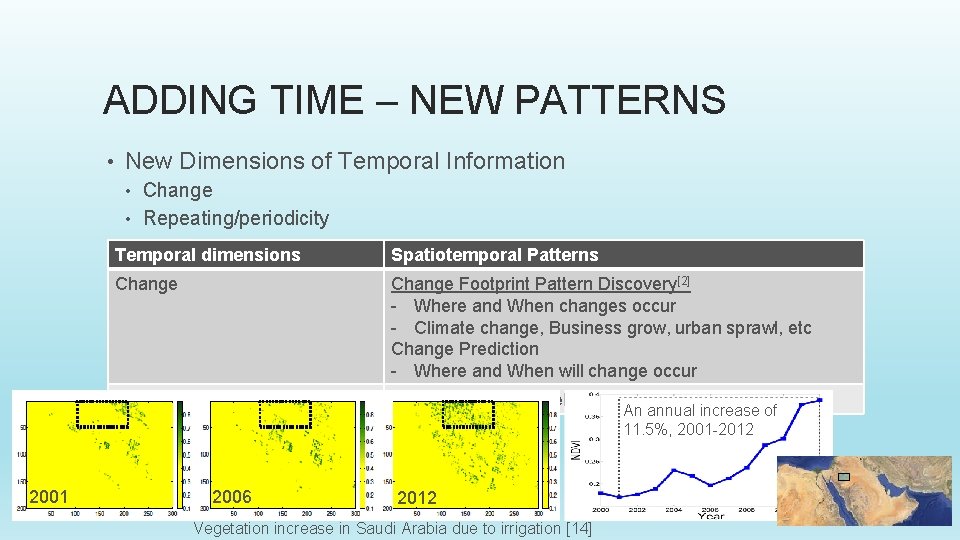
ADDING TIME – NEW PATTERNS • New Dimensions of Temporal Information Change • Repeating/periodicity • 2001 Temporal dimensions Spatiotemporal Patterns Change Footprint Pattern Discovery[2] - Where and When changes occur - Climate change, Business grow, urban sprawl, etc Change Prediction - Where and When will change occur Repeating/periodic Finding periodic travel patterns, schedules, habits 2006 An annual increase of 11. 5%, 2001 -2012 Vegetation increase in Saudi Arabia due to irrigation [14]

CHANGE FOOTPRINT PATTERNS Static Local Time Between snapshots Time Focal Point in time series Time Zonal Interval in time series Time

OUTLINE • Introduction • Spatial Data and Models • Statistical models • Spatial Pattern Families • Computational Challenges

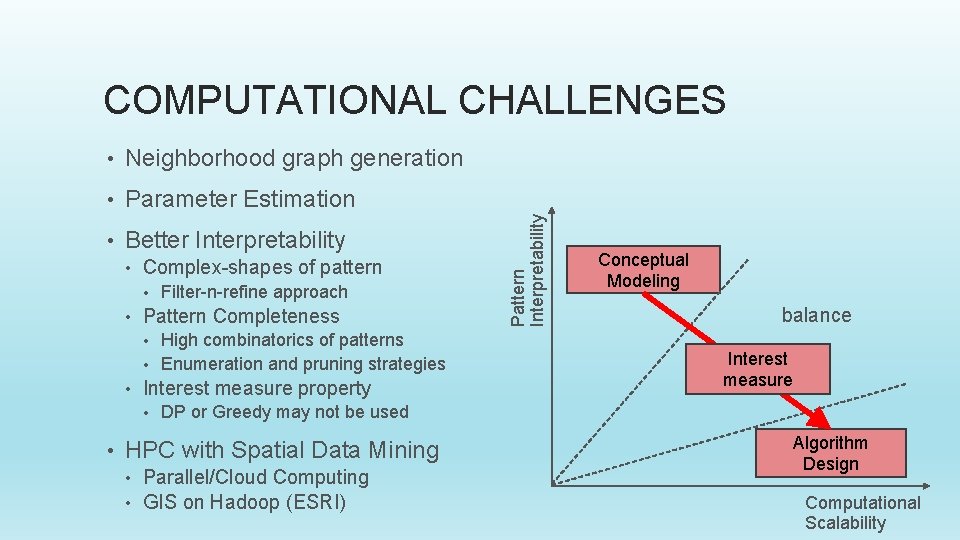
• Neighborhood graph generation • Parameter Estimation • Better Interpretability • Complex-shapes of pattern • • Filter-n-refine approach Pattern Completeness High combinatorics of patterns • Enumeration and pruning strategies • • Interest measure property • • Conceptual Modeling balance Interest measure DP or Greedy may not be used HPC with Spatial Data Mining Parallel/Cloud Computing • GIS on Hadoop (ESRI) • Pattern Interpretability COMPUTATIONAL CHALLENGES Algorithm Design Computational Scalability

SUMMARY • What is SDM and why it’s important • What’s special about spatial • Pattern families, potential directions and applications • Computational Challenges

ACKNOWLEDGEMENT • This presentation is prepared based on materials from Prof. Shashi Shekhar and the Spatial Database and Spatial Data Mining Group at the University of Minnesota (http: //www. spatial. cs. umn. edu/).

REFERENCES AND READINGS [1]. Shekhar, Shashi, et al. "Identifying patterns in spatial information: A survey of methods. " Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 1. 3 (2011): 193 -214. [2]. Xun Zhou, Shashi Shekhar, and Reem Y. Ali. "Spatiotemporal change footprint pattern discovery: an inter‐disciplinary survey. " Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery 4. 1 (2014): 1 -23. [3]. Shashi Shekhar and Sanjay Chawla. Spatial Database: A Tour. Prentice Hall 2003. [4]. Banerjee, Sudipto, Alan E. Gelfand, and Bradley P. Carlin. Hierarchical modeling and analysis for spatial data. CRC Press, 2004. [5]. Jiang, Z. , Shekhar, S. , Zhou, X. , Knight, J. , & Corcoran, J. (2013, December). Focal-test-based spatial decision tree learning: A summary of results. In Data Mining (ICDM), 2013 IEEE 13 th International Conference on (pp. 320 -329). IEEE. [6]. Shekhar, Shashi, Chang-Tien Lu, and Pusheng Zhang. "A unified approach to detecting spatial outliers. " Geo. Informatica 7, no. 2 (2003): 139 -166. [7]. Y Huang, S Shekhar, H Xiong, Discovering colocation patterns from spatial data sets: a general approach. Knowledge and Data Engineering, IEEE Transactions on 16 (12), 1472 -1485 [8]. Ester, Martin; Kriegel, Hans-Peter; Sander, Jörg; Xu, Xiaowei (1996). "A density-based algorithm for discovering clusters in large spatial databases with noise". In Simoudis, Evangelos; Han, Jiawei; Fayyad, Usama M. Proceedings of the Second International Conference on Knowledge Discovery and Data Mining (KDD-96) [9]. Kulldorff, Martin. "A spatial scan statistic. " Communications in Statistics-Theory and methods 26. 6 (1997): 1481 -1496. [10]. Dev Oliver, Shashi Shekhar, Xun Zhou, Emre Eftelioglu, Michael Evans, Qiaodi Zhuang, James Kang, Renee Laubscher and Christopher Farah. Significant Route Discovery: A Summary of Results. In GIScience 2014 (to appear). [11]. Celik, Mete, et al. "Mixed-drove spatiotemporal co-occurrence pattern mining. " Knowledge and Data Engineering, IEEE Transactions on 20. 10 (2008): 1322 -1335. [12]. Mohan, Pradeep, Shashi Shekhar, James A. Shine, and James P. Rogers. "Cascading spatio-temporal pattern discovery. " Knowledge and Data Engineering, IEEE Transactions on 24, no. 11 (2012): 1977 -1992. [13]. Daniel B. Neill, Andrew W. Moore, Maheshkumar Sabhnani, and Kenny Daniel. Detection of emerging space-time clusters. Proceedings of the 11 th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, 218 -227, 2005 [14]. Xun Zhou, Shashi Shekhar, Dev Oliver. "Discovering Persistent Change Windows in Spatiotemporal Datasets: A Summary of Results". In 2 nd ACM SIGSPATIAL International Workshop on Analytics for Big Geospatial Data (Big. Spatial-2013), Nov 5, 2013, Orlando, Florida, USA.