Identifying partial orders in sequences with Galois connections

Data Description • A sequence is an ordered list of sets of items: <(I

Basic Definitions • A general partial order in D is an acyclic directed graph,

Problem Formulation • Goal: to identify partial orders and their support (alternatively, whose support

Problem Formulation • If P’ P we say that P is more specific than

Example Input Seqs where it is contained || 1 2 3 B C D

Motivation • Ordering relationships are useful in many domains: web mining, monitoring of processes,

Addressing the Problem • Observation: Identifying such structures directly from the data is a

A proposal || B C B D , A Set of all seqs. identifying

Result 1 Theorem: sequences identifying maximal paths of the most specific partial orders are

How to construct posets out of closed sequences? || B C D , A

Grouping closed sequences || B C , D A <(b) (c) (d)> A B

Result 2 • It is possible to characterize a closure operator sets of sequences.

Result 2 • A set of sequences S is closed if it coincides with

Result 2 Theorem: closed sets of sequences identify the maximal paths of the same

Conclusions • General partial orders in sequential data can be identified by: – Mining

Slides: 17

Download presentation

Identifying partial orders in sequences (with Galois connections) Gemma Casas Garriga

Data Description • A sequence is an ordered list of sets of items: <(I 1) (I 2) … (IM)> For example, < (a c) (d b) (e) (a) > • We consider a set of sequences D to be analyzed. Id D = {s 1, … , s. N} 1 2 where each si is a sequence. 3 < (a) (b) (c) (d) > < (b) (c) (d) (a) > < (b) (c) (a) (d) >

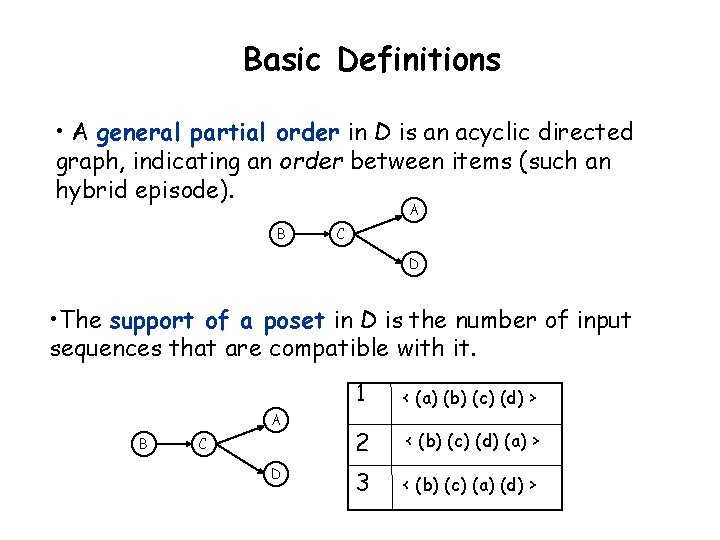
Basic Definitions • A general partial order in D is an acyclic directed graph, indicating an order between items (such an hybrid episode). A B C D • The support of a poset in D is the number of input sequences that are compatible with it. A B C D 1 < (a) (b) (c) (d) > 2 < (b) (c) (d) (a) > 3 < (b) (c) (a) (d) >

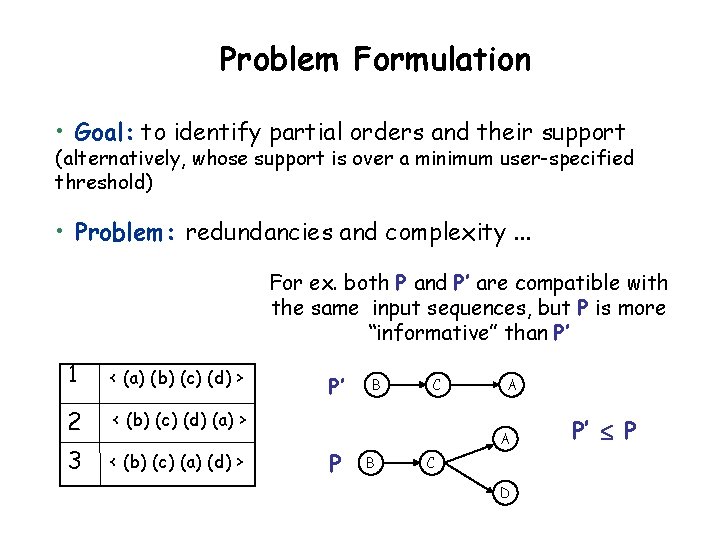
Problem Formulation • Goal: to identify partial orders and their support (alternatively, whose support is over a minimum user-specified threshold) • Problem: redundancies and complexity. . . For ex. both P and P’ are compatible with the same input sequences, but P is more “informative” than P’ 1 < (a) (b) (c) (d) > 2 < (b) (c) (d) (a) > 3 < (b) (c) (a) (d) > P’ P B C A A B C D P’ P

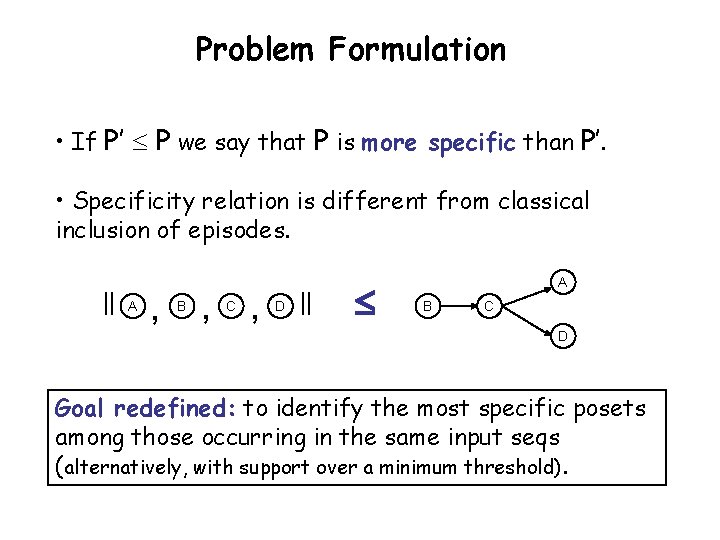
Problem Formulation • If P’ P we say that P is more specific than P’. • Specificity relation is different from classical inclusion of episodes. || A , B , C , D || A B C D Goal redefined: to identify the most specific posets among those occurring in the same input seqs (alternatively, with support over a minimum threshold).

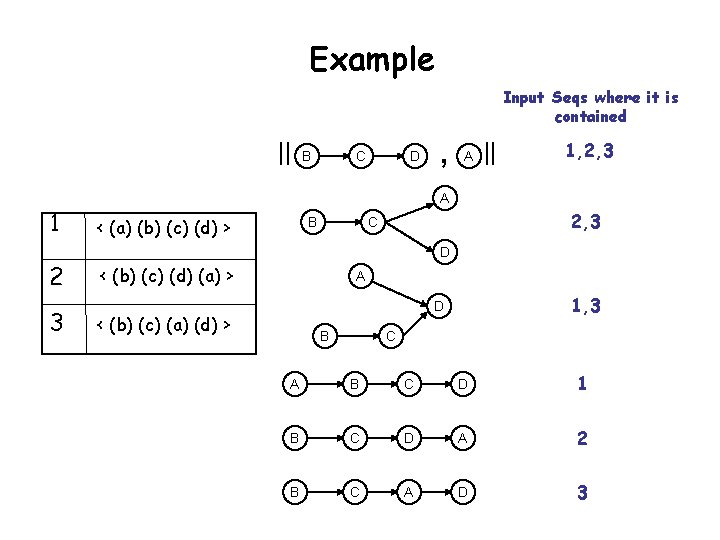
Example Input Seqs where it is contained || 1 2 3 B C D , A || 1, 2, 3 A < (a) (b) (c) (d) > B 2, 3 C D < (b) (c) (d) (a) > A 1, 3 D < (b) (c) (a) (d) > B C A B C D 1 B C D A 2 B C A D 3

Motivation • Ordering relationships are useful in many domains: web mining, monitoring of processes, e-comerce. . . • The most specific episodes give a general view of D, summarizing all the input sequences without redundancies.

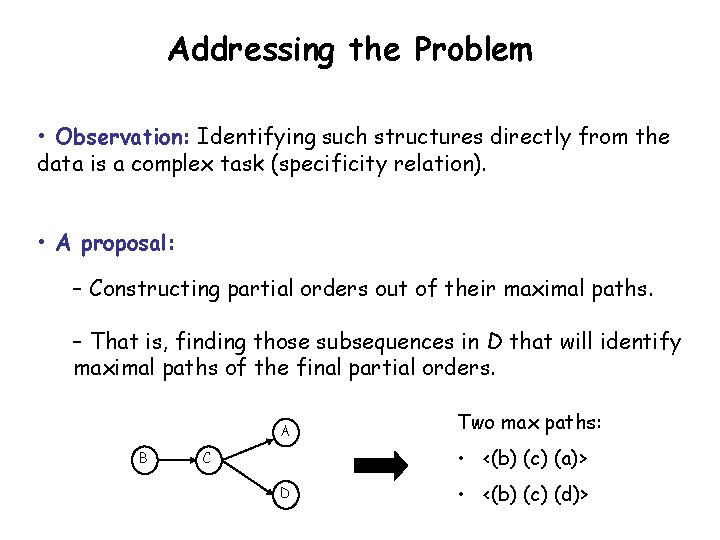
Addressing the Problem • Observation: Identifying such structures directly from the data is a complex task (specificity relation). • A proposal: – Constructing partial orders out of their maximal paths. – That is, finding those subsequences in D that will identify maximal paths of the final partial orders. A B Two max paths: • <(b) (c) (a)> C D • <(b) (c) (d)>

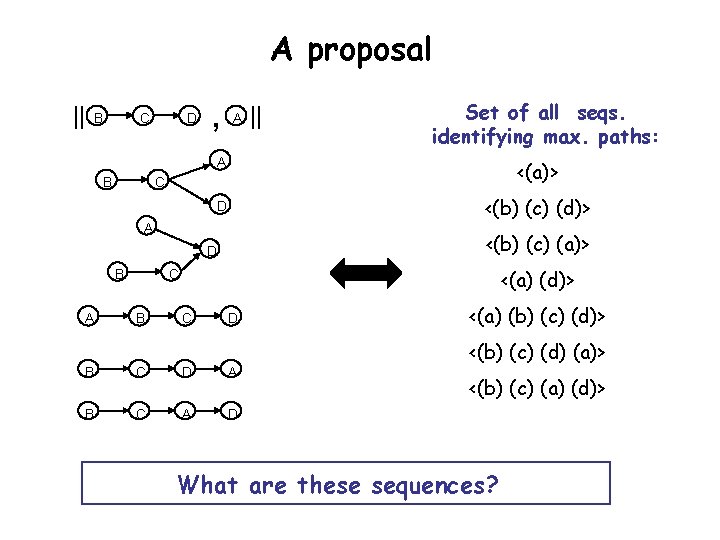
A proposal || B C B D , A Set of all seqs. identifying max. paths: A <(a)> D <(b) (c) (d)> C A <(b) (c) (a)> D B A || <(a) (d)> C B C D A B C A D <(a) (b) (c) (d)> <(b) (c) (d) (a)> <(b) (c) (a) (d)> What are these sequences?

Result 1 Theorem: sequences identifying maximal paths of the most specific partial orders are closed sequential patterns. • Closed sequential patterns (or closed sequences) are maximal among those having the same number of occurences (support) in D. 1 < (a) (b) (c) (d) > • < (a) (d) > is closed. 2 < (b) (c) (d) (a) > 3 < (b) (c) (a) (d) > • < (b) (d) > is not cloased, since it is contained in <(b) (c) (d)> that has the same support. • Some algorithms for minig closed seqs: Clo. Span, BIDE, TSP. . .

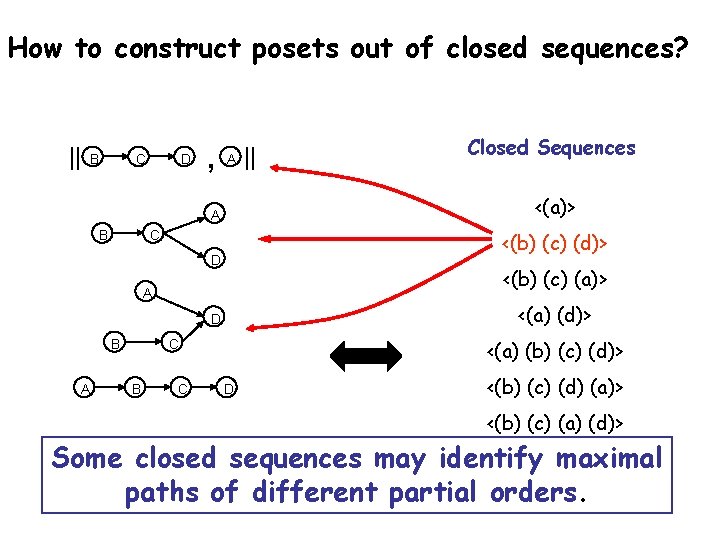
How to construct posets out of closed sequences? || B C D , A <(b) (c) (d)> C D <(b) (c) (a)> A <(a) (d)> D B A <(a) (b) (c) (d)> C B C Closed Sequences <(a)> A B || D <(b) (c) (d) (a)> <(b) (c) (a) (d)> B C D A Some closed sequences may identify maximal paths of different partial orders. B C A D

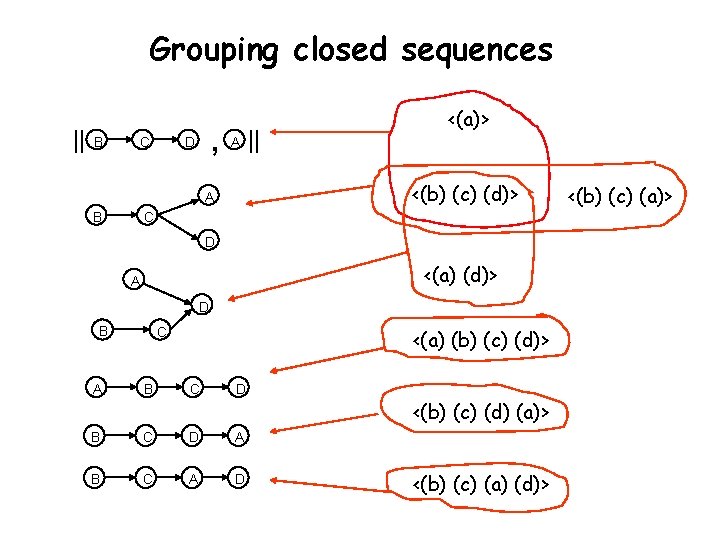
Grouping closed sequences || B C , D A <(b) (c) (d)> A B || <(a)> C D <(a) (d)> A D B C <(a) (b) (c) (d)> A B C D A B C A D <(b) (c) (d) (a)> <(b) (c) (a) (d)> <(b) (c) (a)>

Result 2 • It is possible to characterize a closure operator sets of sequences. working on • A closure operator satisfies the three basic closure axioms: Monotonicity, Extensivity, and Idempotency. • Broadly: Given any set of sequences S, (S) returns the set of maximal sequences that are present in the same input sequences where S is contained. 1 < (a) (b) (c) (d) > 2 < (b) (c) (d) (a) > 3 < (b) (c) (a) (d) > ({< (b) (c) >}) = {<(a)>, <(b) (c) (d)> }

Result 2 • A set of sequences S is closed if it coincides with its closure: (S) = S Lemma: individually, sequences in a closed set S, are closed sequential patterns. 1 < (a) (b) (c) (d) > 2 < (b) (c) (d) (a) > 3 < (b) (c) (a) (d) > ({<(a)>, < (b) (c) (d)>}) = {<(a)>, <(b) (c) (d)> } Both <(a)> and <(b) (c) (d)> are closed sequential patterns.

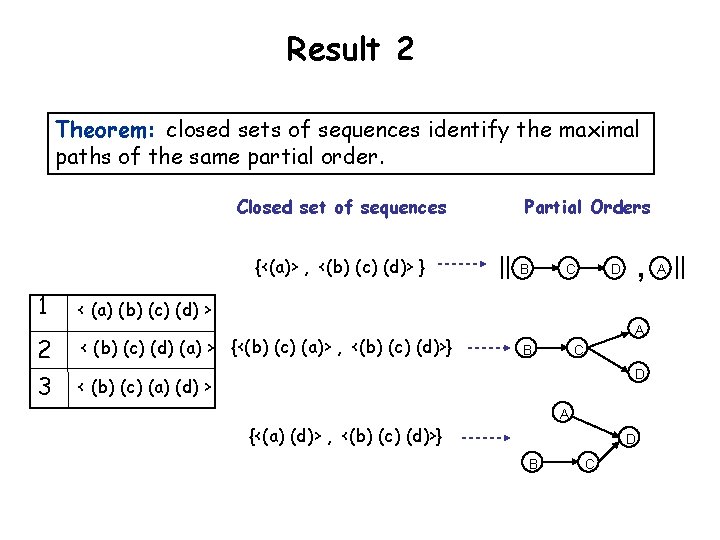
Result 2 Theorem: closed sets of sequences identify the maximal paths of the same partial order. Closed set of sequences {<(a)> , <(b) (c) (d)> } 1 2 3 Partial Orders || B C , D < (a) (b) (c) (d) > < (b) (c) (d) (a) > {<(b) (c) (a)> , <(b) (c) (d)>} A B C D < (b) (c) (a) (d) > A {<(a) (d)> , <(b) (c) (d)>} D B C A ||

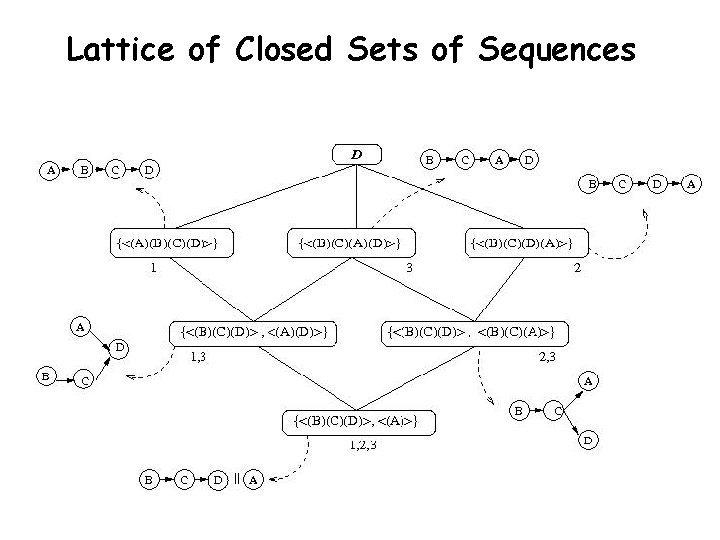
Lattice of Closed Sets of Sequences

Conclusions • General partial orders in sequential data can be identified by: – Mining closed sequential patterns and their support (Clo. Span, BIDE …). – Grouping closed sequential patterns in closed sets of sequences, according to operator . – Getting final partial orders from those agrupations. • This transformation represents an important algorithmic simplification w. r. t. previous approaches of mining episodes directly from the data.