IDENTIFY METRIC UNITS FOR MASS DISTANCE TIME TEMPERATURE

IDENTIFY METRIC UNITS FOR MASS, DISTANCE, TIME, TEMPERATURE, VELOCITY, ACCELERATION, DENSITY, FORCE, ENERGY & POWER COS 12. 0

WHAT YOU’LL LEARN • • • Name the prefixes used in SI & indicate what multiple of ten each one represents. Identify SI units and symbols for mass, length (distance), time, temperature, velocity, acceleration, density, force, energy & power. Convert related SI units. Use scientific notation & significant figures in problem solving. Identify the significant figures in calculations. Understand the difference between precision & accuracy

UNITS OF MEASUREMENT What is a measurement? • A measurement is a number and a unit. • 14. 5 meters, 35 dozen, and 1 hour are all measurements.

DEFINITIONS

DERIVED UNIT • measurement unit using a combination of units • g/cm 3, m/s 2, m/s, g/ml, k. W

DISTANCE (LENGTH) • measure of straight-line distance between two points • meter, kilometer, mile

MASS • measure of amount of matter in an object

TIME • measured period during which an action, process, or condition exists or continues • seconds, minutes, hours, days, years…

TEMPERATURE • measure of average kinetic energy of all particles in an object • Kelvin • absolute zero (0 K) • coldest possible temperature • = -273°C

VELOCITY • measures the speed & direction of a moving object

ACCELERATION • rate of change of velocity, occurs if an object speeds up, changes direction or slows down

FORCE • push or pull that one body exerts on another

ENERGY • capacity to do work

POWER • amount of work done or energy transferred

ELECTRIC CURRENT • flow of electric charge through a wire or conductor

DENSITY • mass per unit volume of a material

VOLUME • amount of space occupied by an object • unit is liter • 1 ml = 1 cm 3

WEIGHT • measure of gravitational force exerted on an object

JOULE • SI unit of energy measuring heat, electricity and mechanical work

WATT • SI deried unit of power, equal to one joule of energy per second. • measures a rate of energy use or production.

NEWTON • SI derived unit of force

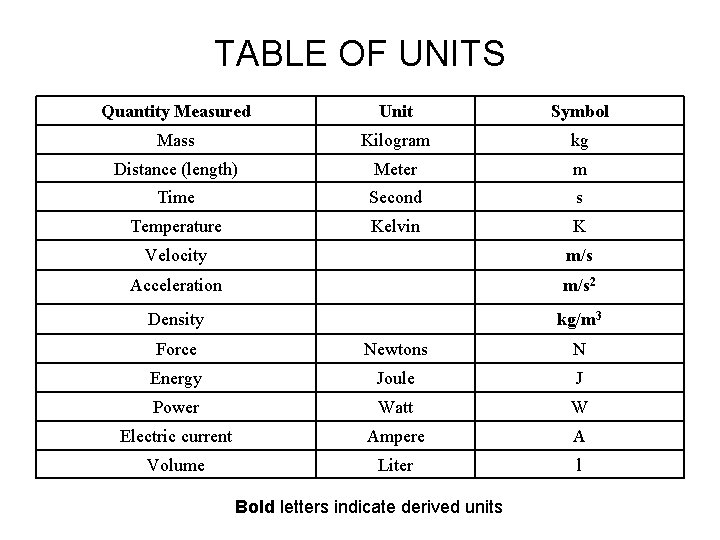
TABLE OF UNITS Quantity Measured Unit Symbol Mass Kilogram kg Distance (length) Meter m Time Second s Temperature Kelvin K Velocity m/s Acceleration m/s 2 Density kg/m 3 Force Newtons N Energy Joule J Power Watt W Electric current Ampere A Volume Liter l Bold letters indicate derived units

SIGNIFICANT FIGURES

SIGNIFICANT FIGURES Significant figure • prescribed decimal place that determines the amount of rounding off to be done based on the precision of the measurement Precision • exactness of a measurement Accuracy • description of how close a measurement is to the true value of the quantity measured

Chapter 1 Accuracy and Precision

Chapter 1 Accuracy and Precision

Rules For Significant Digits from 1 -9 are always significant. ¢ Zeros between two other significant digits are always significant ¢ One or more additional zeros to the right of both the decimal place and another significant digit are significant. ¢ Zeros used solely for spacing the decimal point (placeholders) are not significant. ¢

EXAMPLES OF SIGNIFICANT DIGITS EXAMPLES # OF SIG. DIG. COMMENT 453 kg 3 All non-zero digits are always significant. 5057 L 4 Zeros between 2 sig. dig. are significant. 5. 00 3 Additional zeros to the right of decimal and a sig. dig. are significant. 0. 007 1 Placeholders are not sig.

Multiplying and Dividing • • RULE: When multiplying or dividing, your answer may only show as many significant digits as the multiplied or divided measurement showing the least number of significant digits. Example: When multiplying 22. 37 cm x 3. 10 cm x 85. 75 cm = 5946. 50525 cm 3 We look to the original problem and check the number of significant digits in each of the original measurements: 22. 37 shows 4 significant digits. 3. 10 shows 3 significant digits. 85. 75 shows 4 significant digits. Our answer can only show 3 significant digits because that is the least number of significant digits in the original problem. 5946. 50525 shows 9 significant digits, we must round to the tens place in order to show only 3 significant digits. Our final answer becomes 5950 cm 3.

Adding and Subtracting • • • RULE: When adding or subtracting your answer can only show as many decimal places as the measurement having the fewest number of decimal places. Example: When we add 3. 76 g + 14. 83 g + 2. 1 g = 20. 69 g We look to the original problem to see the number of decimal places shown in each of the original measurements. 2. 1 shows the least number of decimal places. We must round our answer, 20. 69, to one decimal place (the tenth place). Our final answer is 20. 7 g

SCIENTIFIC NOTATION

Scientific Notation • • The number 123, 000, 000 in scientific notation is written as : 1. 23 x 1011 The first number 1. 23 is called the coefficient. It must be greater than or equal to 1 and less than 10. The second number is called the base. It must always be 10 in scientific notation. The base number 10 is always written in exponent form. In the number 1. 23 x 1011 the number 11 is referred to as the exponent or power of ten.

Scientific Notation • • To write a number in scientific notation: Put decimal after first digit and drop zeroes. 1. 2300000 In number 123, 000, 000 coefficient will be 1. 23 To find exponent count number of places from decimal to the end of number. In 123, 000, 000 there are 11 places. Therefore we write 123, 000, 000 as: 1. 23 x 1011

Scientific Notation • • For small numbers we use a similar approach. Numbers smaller than 1 will have a negative exponent. A millionth of a second (. 000001) is: 1. 0 x 10 -6

Standard Form • • Is just opposite of scientific notation! 6. 33 X 108 = 633, 000 All we’ve done is moved decimal eight (8) places to right. 5. 18 X 10 -7 =. 000000518 All we’ve done is moved decimal seven (7) places to left. IT’S THAT EASY!

Write the following in scientific notation: • • • 4, 100, 000 = ________ 4. 1 x 106 345, 600, 000 = _____ 3. 456 x 1011 0. 0456= ________ 4. 56 x 10 -2 0. 00000012=______ 1. 2 x 10 -7 0. 00305= ______ 3. 05 x 10 -3

Write the following in standard form: • • • 4. 67 x 103 =_________ 4670 3. 112 x 105 = _________ 311200 3. 112 x 10 -4 = ________ 0. 0003112 4 x 10 -6 = __________ 0. 000004 1 x 1011 = _________ 100, 000, 000

STANDARDS OF MEASUREMENT

WHY SI UNITS? metric • standard of measurement (for most nations) • each type of SI measurement has a base unit • fundamental unit of measurement which are used to form other, compound units for other quantities. (SI base unit)

What does SI stand for? n international system of units

SI PREFIXES n Easy to use because it is based on multiples of ten.

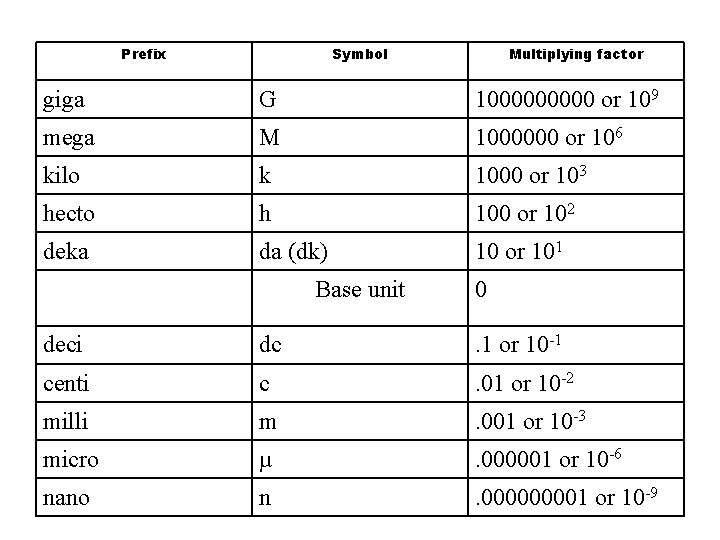
Prefix Symbol Multiplying factor giga G 100000 or 109 mega M 1000000 or 106 kilo k 1000 or 103 hecto h 100 or 102 deka da (dk) 10 or 101 Base unit 0 deci dc . 1 or 10 -1 centi c . 01 or 10 -2 milli m . 001 or 10 -3 micro µ . 000001 or 10 -6 nano n . 00001 or 10 -9

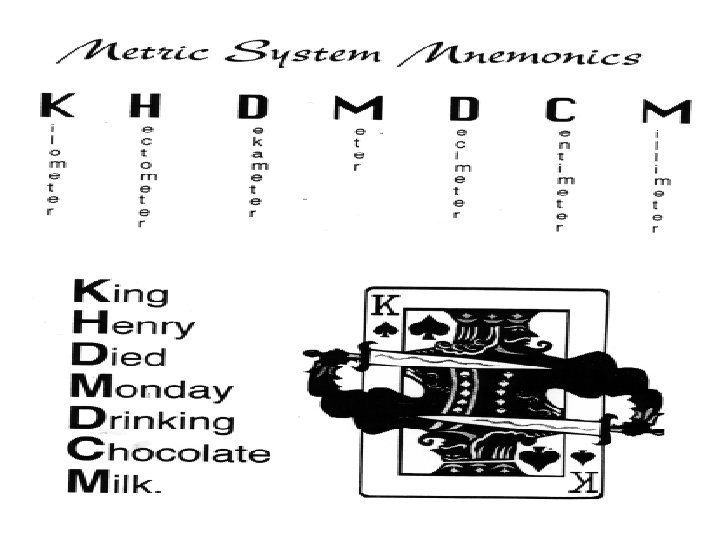
KHDODCM • • • Changing from one metric unit to another is called metric conversion “M” is the space where meter, liter, or gram belongs or base unit (0) Let’s practice! To change from one metric unit to another, we simply move the decimal point. For example: 25. 4 km = ? cm • • K-H-D-O-D-C is 5 places to the right 25. 4 km = 2, 540, 000 cm

KHDODCM • • • 30 cm = ? hm C – D- O –D- H is 4 places to the left 30 cm = 0. 0030 hm (this is the same as 0. 003 hm) • • • 14 dal = _____dl D- O –D is 2 places to the right 14 dal = 1400 dl Find the difference between the exponents of the two prefixes. Move the decimal that many places.

SI Prefix Conversions 0. 2 20 cm = _______m 32 0. 032 A = _______ m. A 45, 000 45 m = _______ nm 0. 0805 km 805 dm = _____