Identify a Point of Continuity Determine whether is

  • Slides: 27
Download presentation

Identify a Point of Continuity Determine whether is continuous at . Justify using the

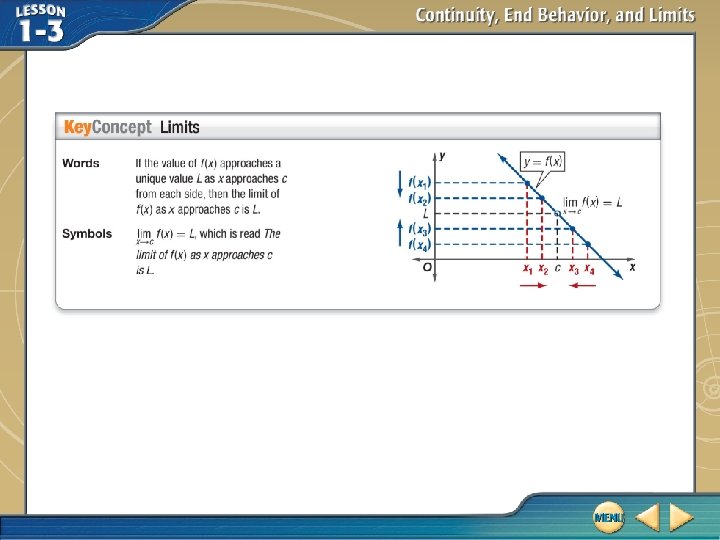
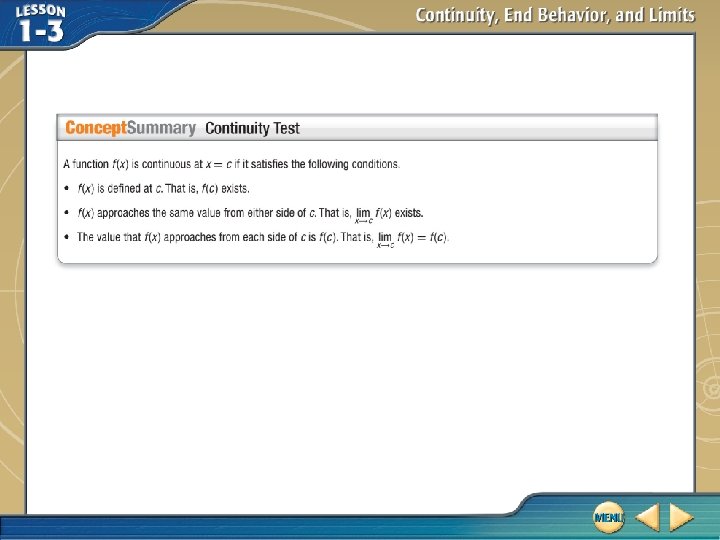
Identify a Point of Continuity Determine whether is continuous at . Justify using the continuity test. Check the three conditions in the continuity test. 1. Does Because exist? , the function is defined at

Identify a Point of Continuity 2. Does exist? Construct a table that shows values

Identify a Point of Continuity 2. Does exist? Construct a table that shows values of f(x) approaching from the left and from the right. The pattern of outputs suggests that as the value of x gets close to from the left and from the right, f(x) gets closer to. . So we estimate that

Identify a Point of Continuity 3. Does Because ? is estimated to be we

Identify a Point of Continuity 3. Does Because ? is estimated to be we conclude that f (x) is continuous at and. The graph of f (x) below supports this conclusion.

Identify a Point of Continuity Answer: 1. 2. 3. exists. . f (x) is

Identify a Point of Continuity Answer: 1. 2. 3. exists. . f (x) is continuous at .

Determine whether the function f (x) = x 2 + 2 x – 3

Determine whether the function f (x) = x 2 + 2 x – 3 is continuous at x = 1. Justify using the continuity test. A. continuous; f (1) B. Discontinuous; the function is undefined at x = 1 because does not exist.

Identify a Point of Discontinuity A. Determine whether the function is continuous at x

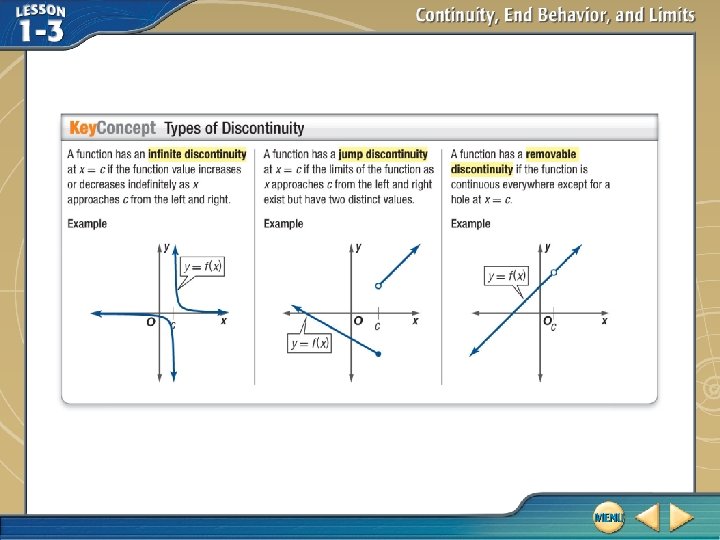
Identify a Point of Discontinuity A. Determine whether the function is continuous at x = 1. Justify using the continuity test. If discontinuous, identify the type of discontinuity as infinite, jump, or removable. 1. Because is undefined, f (1) does not exist.

Identify a Point of Discontinuity 2. Investigate function values close to f(1). The pattern

Identify a Point of Discontinuity 2. Investigate function values close to f(1). The pattern of outputs suggests that for values of x approaching 1 from the left, f (x) becomes increasingly more negative. For values of x approaching 1 from the right, f (x) becomes increasing more positive. Therefore, does not exist.

Identify a Point of Discontinuity 3. Because f (x) decreases without bound as x

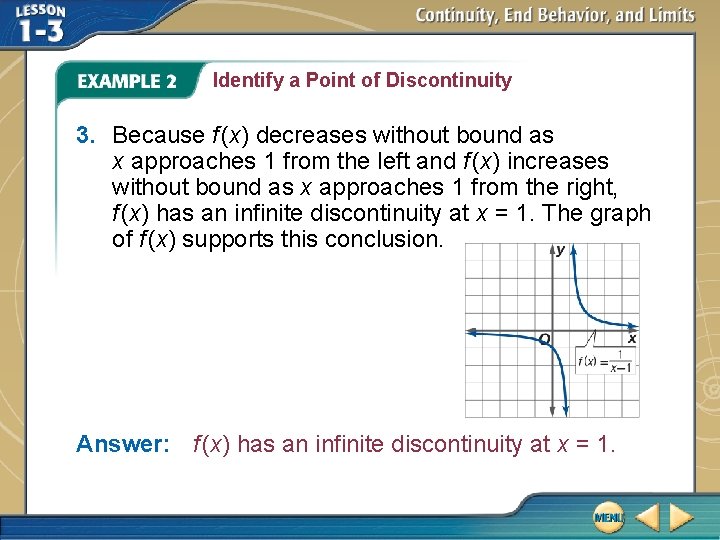
Identify a Point of Discontinuity 3. Because f (x) decreases without bound as x approaches 1 from the left and f (x) increases without bound as x approaches 1 from the right, f (x) has an infinite discontinuity at x = 1. The graph of f (x) supports this conclusion. Answer: f (x) has an infinite discontinuity at x = 1.

Identify a Point of Discontinuity B. Determine whether the function is continuous at x

Identify a Point of Discontinuity B. Determine whether the function is continuous at x = 2. Justify using the continuity test. If discontinuous, identify the type of discontinuity as infinite, jump, or removable. 1. Because is undefined, f (2) does not exist. Therefore f (x) is discontinuous at x = 2.

Identify a Point of Discontinuity 2. Investigate function values close to f (2). The

Identify a Point of Discontinuity 2. Investigate function values close to f (2). The pattern of outputs suggests that f (x) approaches 0. 25 as x approaches 2 from each side, so .

Identify a Point of Discontinuity 3. Because exists, but f (2) is undefined, f

Identify a Point of Discontinuity 3. Because exists, but f (2) is undefined, f (x) has a removable discontinuity at x = 2. The graph of f (x) supports this conclusion. 4 Answer: f (x) is discontinuous at x = 2 with a removable discontinuity.

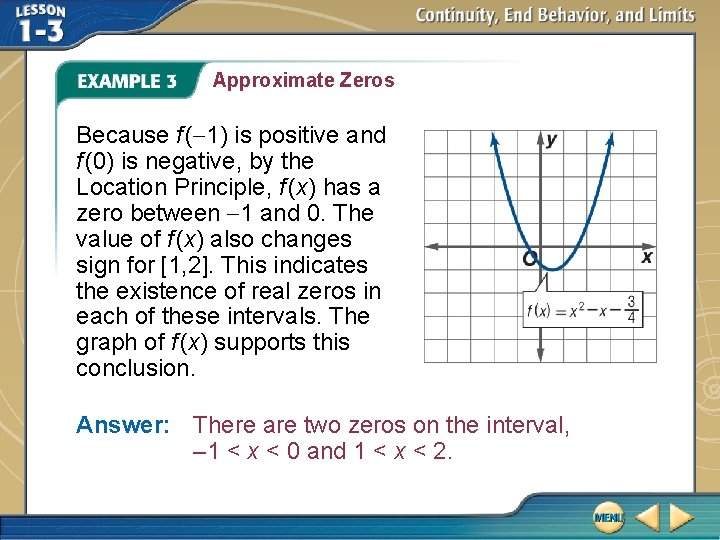
Approximate Zeros A. Determine between which consecutive integers the real zeros of are located

Approximate Zeros A. Determine between which consecutive integers the real zeros of are located on the interval [– 2, 2]. Investigate function values on the interval [-2, 2].

Approximate Zeros Because f (-1) is positive and f (0) is negative, by the

Approximate Zeros Because f (-1) is positive and f (0) is negative, by the Location Principle, f (x) has a zero between -1 and 0. The value of f (x) also changes sign for [1, 2]. This indicates the existence of real zeros in each of these intervals. The graph of f (x) supports this conclusion. Answer: There are two zeros on the interval, – 1 < x < 0 and 1 < x < 2.

Approximate Zeros B. Determine between which consecutive integers the real zeros of f (x)

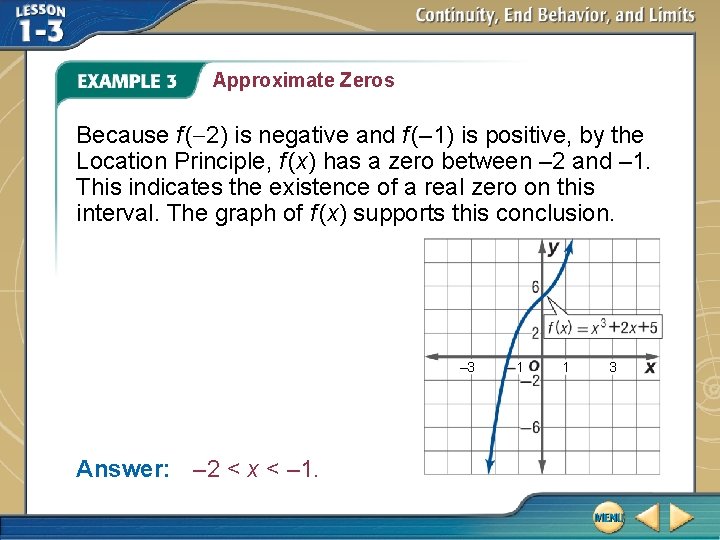
Approximate Zeros B. Determine between which consecutive integers the real zeros of f (x) = x 3 + 2 x + 5 are located on the interval [– 2, 2]. Investigate function values on the interval [– 2, 2].

Approximate Zeros Because f (-2) is negative and f (– 1) is positive, by

Approximate Zeros Because f (-2) is negative and f (– 1) is positive, by the Location Principle, f (x) has a zero between – 2 and – 1. This indicates the existence of a real zero on this interval. The graph of f (x) supports this conclusion. – 3 Answer: – 2 < x < – 1. 1 1 3

Graphs that Approach Infinity Use the graph of f(x) = x 3 – x

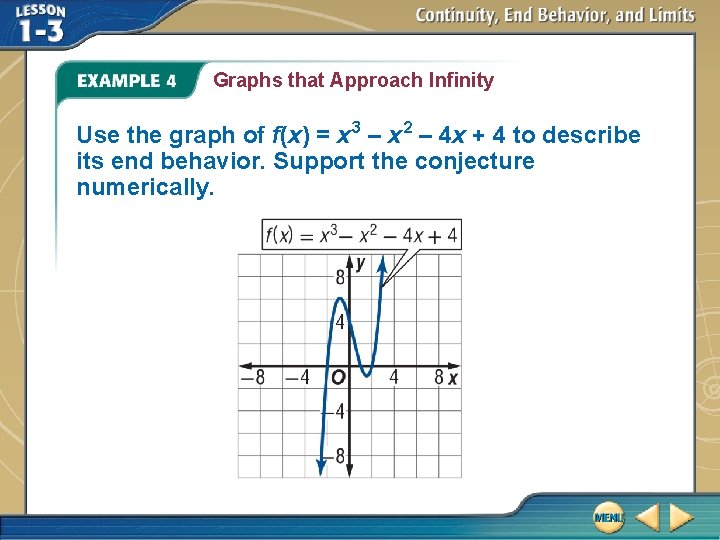
Graphs that Approach Infinity Use the graph of f(x) = x 3 – x 2 – 4 x + 4 to describe its end behavior. Support the conjecture numerically.

Graphs that Approach Infinity Analyze Graphically In the graph of f (x), it appears

Graphs that Approach Infinity Analyze Graphically In the graph of f (x), it appears that and Support Numerically Construct a table of values to investigate function values as |x| increases. That is, investigate the value of f (x) as the value of x becomes greater and greater or more and more negative.

Graphs that Approach Infinity The pattern of outputs suggests that as x approaches –∞,

Graphs that Approach Infinity The pattern of outputs suggests that as x approaches –∞, f (x) approaches –∞ and as x approaches ∞, f (x) approaches ∞. Answer:

Use the graph of f (x) = x 3 + x 2 – 2

Use the graph of f (x) = x 3 + x 2 – 2 x + 1 to describe its end behavior. Support the conjecture numerically. A. B. C. D.

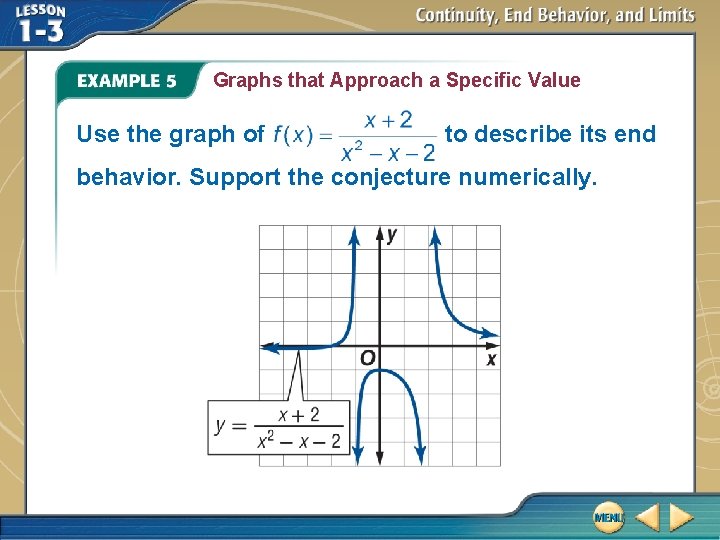
Graphs that Approach a Specific Value Use the graph of to describe its end

Graphs that Approach a Specific Value Use the graph of to describe its end behavior. Support the conjecture numerically.

Graphs that Approach a Specific Value Analyze Graphically In the graph of f (x),

Graphs that Approach a Specific Value Analyze Graphically In the graph of f (x), it appears that. Support Numerically As. As supports our conjecture. . This

Graphs that Approach a Specific Value Answer:

Graphs that Approach a Specific Value Answer:

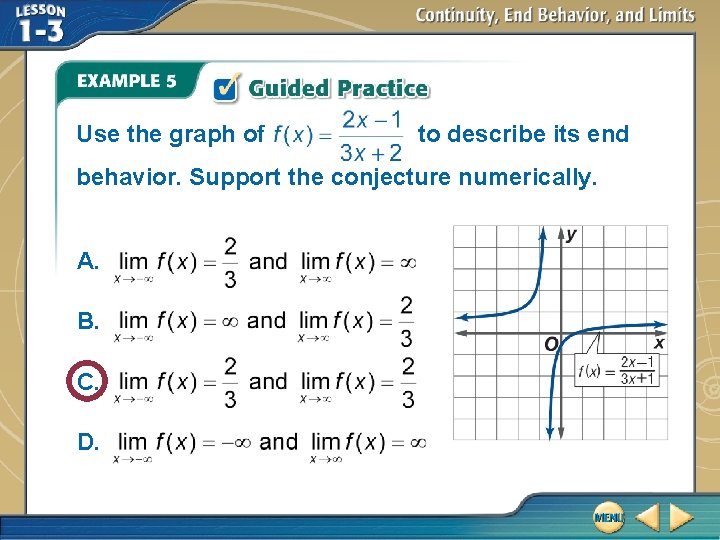
Use the graph of to describe its end behavior. Support the conjecture numerically. A.

Use the graph of to describe its end behavior. Support the conjecture numerically. A. B. C. D.

We wonder whether the whether Will whether theWe wonder whether the whether Will whether the
BUSINESS CONTINUITY Business continuity definition Business Continuity ManagementBUSINESS CONTINUITY Business continuity definition Business Continuity Management
CONTINUITY TASKS What is continuity Continuity is theCONTINUITY TASKS What is continuity Continuity is the
Continuity 1 Determine whether the function is continuousContinuity 1 Determine whether the function is continuous
1 4 Continuity OneSided Limits 1 Determine continuity1 4 Continuity OneSided Limits 1 Determine continuity
1 6 Continuity Objectives To determine continuity of1 6 Continuity Objectives To determine continuity of
Identify Parallelograms Determine whether the quadrilateral is aIdentify Parallelograms Determine whether the quadrilateral is a
Identify Parallelograms Determine whether the quadrilateral is aIdentify Parallelograms Determine whether the quadrilateral is a
Identify Arithmetic Sequences A Determine whether the sequenceIdentify Arithmetic Sequences A Determine whether the sequence
Identify Functions Using Tables Determine whether the tableIdentify Functions Using Tables Determine whether the table
DoNow Determine whether the given point is aDoNow Determine whether the given point is a
Whether the weather is fine Or whether theWhether the weather is fine Or whether the
Whether The Weather Whether the weather be fineWhether The Weather Whether the weather be fine
Whether its cold or whether its hot weWhether its cold or whether its hot we
Digital Continuity An introduction Digital continuity The abilityDigital Continuity An introduction Digital continuity The ability
What is Continuity of Operations Planning Continuity ofWhat is Continuity of Operations Planning Continuity of
Business Continuity Basics David Tickner MBCI Business ContinuityBusiness Continuity Basics David Tickner MBCI Business Continuity
Continuity of Operations COOP Maureen Clement Statewide ContinuityContinuity of Operations COOP Maureen Clement Statewide Continuity
DC and Parametric Tests Continuity Purpose of ContinuityDC and Parametric Tests Continuity Purpose of Continuity
2 3 Continuity and Intermediate Value Theorem Continuity2 3 Continuity and Intermediate Value Theorem Continuity
Business Continuity Planning at CSULB Business Continuity ServicesBusiness Continuity Planning at CSULB Business Continuity Services
Predict changes Predict continuity An important economic continuityPredict changes Predict continuity An important economic continuity
A 4 CONTINUITY Investigating Continuity Continuous Function AA 4 CONTINUITY Investigating Continuity Continuous Function A
Copper Stabilizer Continuity Measurement Project Copper Stabilizer ContinuityCopper Stabilizer Continuity Measurement Project Copper Stabilizer Continuity