ICS 241 Discrete Mathematics II William Albritton Information

ICS 241 • Discrete Mathematics II – William Albritton, Information and Computer Sciences Department at University of Hawai’i at Manoa – For use with Kenneth H. Rosen’s Discrete Mathematics & Its Applications (5 th Edition) – Based on slides originally created by • Dr. Michael P. Frank, Department of Computer & Information Science & Engineering at University of Florida 1/10/2022 1

Discrete Mathematics II • “Discrete” ( “discreet”!) – Composed of distinct, separable parts • Opposite of continuous. • discrete: continuous : : digital: analog • “Discrete Mathematics” – The study of discrete, mathematical objects and structures. 1/10/2022 2

Why Study Discrete Math? • The basis of all of digital information processing is: – Discrete manipulations of discrete structures represented in memory. • It’s the basic language and conceptual foundation for all of computer science. – Discrete math concepts are also widely used throughout math, science, engineering, economics, biology, sociology, communications, etc. , … • A generally useful tool for rational thought! 1/10/2022 3

Uses for Discrete Math in ICS • Advanced algorithms & data structures • Programming language compilers & interpreters. • Computer networks • Computer architecture 1/10/2022 • Database management systems • Cryptography • Error correction codes • Graphics & animation algorithms, game engines, etc. … 4

Chapter 6. 1: Recurrence Relations • A recurrence relation (R. R. ) for a sequence {an} is an equation that expresses an in terms of one or more previous elements a 0, …, an− 1 of the sequence, for all n≥n 0. – I. e. , just a recursive definition, without the base cases. • A particular sequence (described non-recursively) is said to solve the given recurrence relation if it is consistent with the definition of the recurrence. – A given recurrence relation may have many solutions. 1/10/2022 5

Recurrence Relation Example • The recurrence relation an = 2 an− 1 − an− 2 (n≥ 2) • With initial conditions ao = 0 a 1 = 3 • Has the following terms a 2 = 2 a 1 − a 0 = 2(3) – 0 = 6 a 3 = 2 a 2 − a 1 = 2(6) – 3 = 12 – 3 = 9 a 4 = 2 a 3 − a 2 = 2(9) – 6 = 18 – 6 = 12 etc … 1/10/2022 6

Recurrence Relation Example • Consider the recurrence relation an = 2 an− 1 − an− 2 (n≥ 2). • Which of the following are solutions? an = 3 n Yes: an=2(3(n-1))-3(n-2)=3 n an = 2 n No: a 2=2(a 1)-a 0; (4) != 2(2)-1 an = 5 Yes: an=2(5)-5=5 1/10/2022 7

Class Exercise • Section 6. 1, Exercise 7. a. (p. 409) – Each pair of students should use only one sheet of paper while solving the class exercises 1/10/2022 8

Solving Compound Interest RR • Recurrence relation for growth of a bank account with P% interest per given period: Mn = Mn− 1 + (P/100)Mn− 1 = (1 + P/100) Mn− 1 = r Mn− 1 (let r = 1 + P/100) = r (r Mn− 2) = r·r·(r Mn− 3) …and so on to… n. M = r 1/10/2022 0 9

Compound Interest Example • After 10 years, how much money will be in a bank account with an initial deposit of $1000 with interest compounded annually at 2% per year? Mn = rn M 0 = (1 + P/100)n M 0 M 10 = (1 + 2/100)10 1000 = 1218. 99 1/10/2022 10

Class Exercise • Section 6. 1, Exercise 11. a. b. (p. 409) – Each pair of students should use only one sheet of paper while solving the class exercises 1/10/2022 11

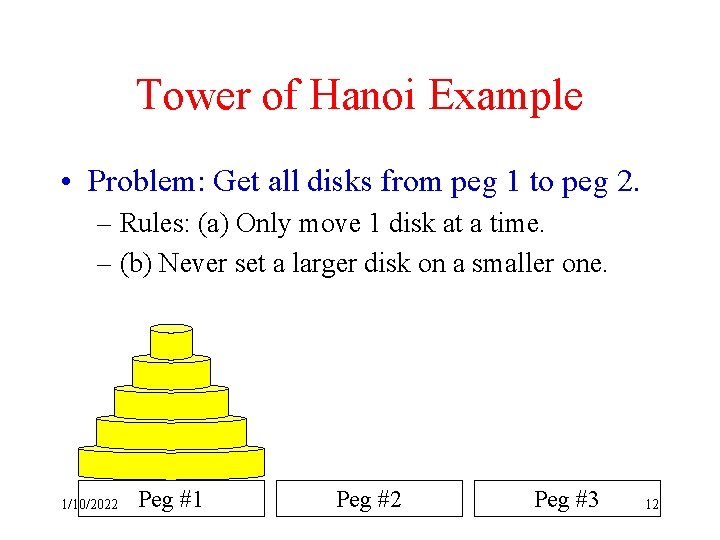
Tower of Hanoi Example • Problem: Get all disks from peg 1 to peg 2. – Rules: (a) Only move 1 disk at a time. – (b) Never set a larger disk on a smaller one. 1/10/2022 Peg #1 Peg #2 Peg #3 12

Hanoi Recurrence Relation • Let Hn = # moves for a stack of n disks. • Here is the optimal strategy: – Move top n− 1 disks to spare peg. (Hn− 1 moves) – Move bottom disk. (1 move) – Move top n− 1 to bottom disk. (Hn− 1 moves) • Note that: Hn = 2 Hn− 1 + 1 – The # of moves is described by a Rec. Rel. 1/10/2022 13

Solving Tower of Hanoi RR Hn = 2 Hn− 1 + 1 = 2 (2 Hn− 2 + 1) + 1 = 22 Hn− 2 + 1 = 22(2 Hn− 3 + 1) + 2 + 1 = 23 Hn− 3 + 22 + 1 … = 2 n− 1 H 1 + 2 n− 2 + … + 2 + 1 = 2 n− 1 + 2 n− 2 + … + 2 + 1 (since H 1 = 1) = (see sum of a geometric series formula, p. 231) = 2 n − 1 1/10/2022 14

Class Exercise • Section 6. 1, Exercise 9. c. (p. 409) – Each pair of students should use only one sheet of paper while solving the class exercises • Hint: use formula for sum of first n positive integers: 1 + 2 + … + n = n(n+1)/2 • Exercise 9. d. (p. 409) 1/10/2022 15

Another R. R. Example • Find a R. R. & initial conditions for the number of bit strings of length n without two consecutive 0 s. • We can solve this by breaking down the strings to be counted into cases that end in 0 and in 1. – For each ending in 0, the previous bit must be 1, and before that comes any qualifying string of length n− 2. – For each string ending in 1, it starts with a qualifying string of length n− 1. • Thus, an = an− 1 + an− 2. (Fibonacci recurrence. ) – The initial conditions are: a 0 = 1 (ε), a 1 = 2 (0 and 1). 1/10/2022 (n− 2 bits) 1 0 (n− 1 bits) 1 16

Yet another R. R. example… • Give a recurrence (and base cases) for the number of n-digit decimal strings containing an even number of 0 digits. • Can break down into the following cases: – Any valid string of length n− 1 digits, with any digit 1 -9 appended. – Any invalid string of length n− 1 digits, + zero. • an = 9 an− 1 + (10 n− 1 − an− 1) = 8 an− 1 + 10 n− 1. – Base cases: a 0 = 1 (ε), a 1 = 9 (1 -9). 1/10/2022 17

Class Exercise • Section 6. 1, Exercise 23. a. b. c (p. 410) – Each pair of students should use only one sheet of paper while solving the class exercises • Section 6. 1, Exercise 29. a. b. c (p. 410) 1/10/2022 18