ICS 241 Discrete Mathematics II William Albritton Information

ICS 241 • Discrete Mathematics II – William Albritton, Information and Computer Sciences Department at University of Hawai’i at Manoa – For use with Kenneth H. Rosen’s Discrete Mathematics & Its Applications (5 th Edition) – Based on slides originally created by • Dr. Michael P. Frank, Department of Computer & Information Science & Engineering at University of Florida 1/6/2022 1

Section 9. 3: Tree Traversal • Universal address systems • Traversal algorithms – Preorder traversal – Inorder traversal – Postorder traversal • Infix/prefix/postfix notation 1/6/2022 2

Universal Address Systems • A way to label the nodes of an ordered rooted tree – Label the root with integer 0 – Label its children from left to right with 1, 2, 3, … – For the next level down from vertex A, label its children with A. 1, A. 2, A. 3, … 1/6/2022 3

Traversal Algorithms • Methods for visiting every node of an ordered rooted tree – Most common traversals: • Preorder traversal • Inorder traversal • Postorder traversal 1/6/2022 4

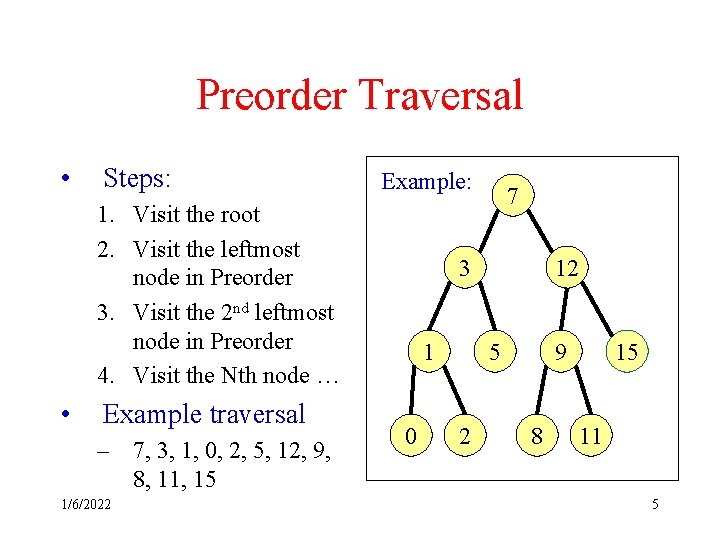
Preorder Traversal • Steps: Example: 1. Visit the root 2. Visit the leftmost node in Preorder 3. Visit the 2 nd leftmost node in Preorder 4. Visit the Nth node … • Example traversal – 7, 3, 1, 0, 2, 5, 12, 9, 8, 11, 15 1/6/2022 7 3 1 0 12 5 2 9 8 15 11 5

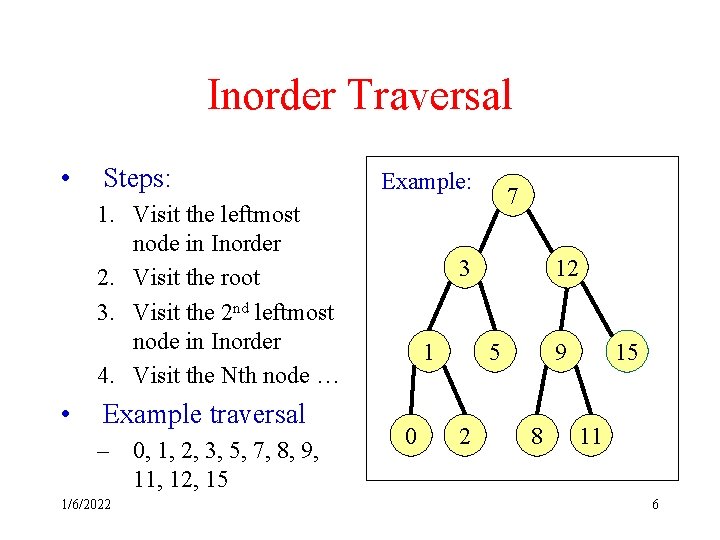
Inorder Traversal • Steps: Example: 1. Visit the leftmost node in Inorder 2. Visit the root 3. Visit the 2 nd leftmost node in Inorder 4. Visit the Nth node … • Example traversal – 0, 1, 2, 3, 5, 7, 8, 9, 11, 12, 15 1/6/2022 7 3 1 0 12 5 2 9 8 15 11 6

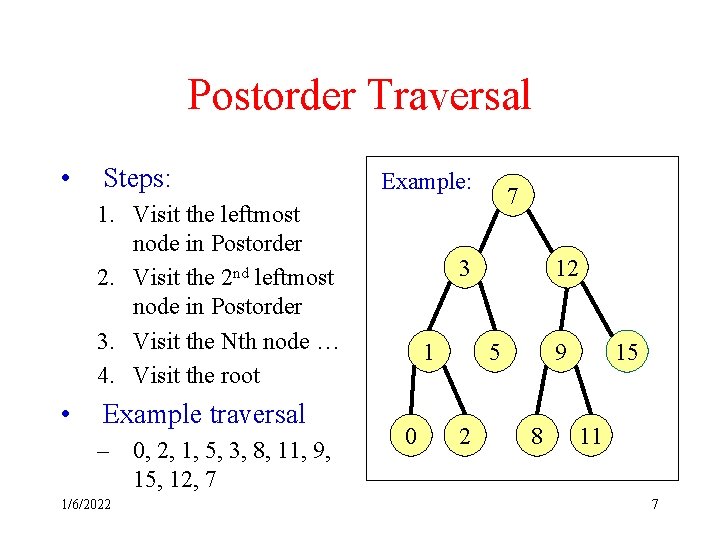
Postorder Traversal • Steps: Example: 1. Visit the leftmost node in Postorder 2. Visit the 2 nd leftmost node in Postorder 3. Visit the Nth node … 4. Visit the root • Example traversal – 0, 2, 1, 5, 3, 8, 11, 9, 15, 12, 7 1/6/2022 7 3 1 0 12 5 2 9 8 15 11 7

Class Exercise • Exercise 7. (p. 673) – Find the pre, in, and postorder traversals • Each pair of students should use only one sheet of paper while solving the class exercises 1/6/2022 8

Infix/Prefix/Postfix Notation • Can use an ordered, rooted tree to represent arithmetic expressions – Leaves represent variables or numbers – Interior nodes represent operations – Operations are evaluated from the bottom of the tree to the top, and from the left node to the right node 1/6/2022 9

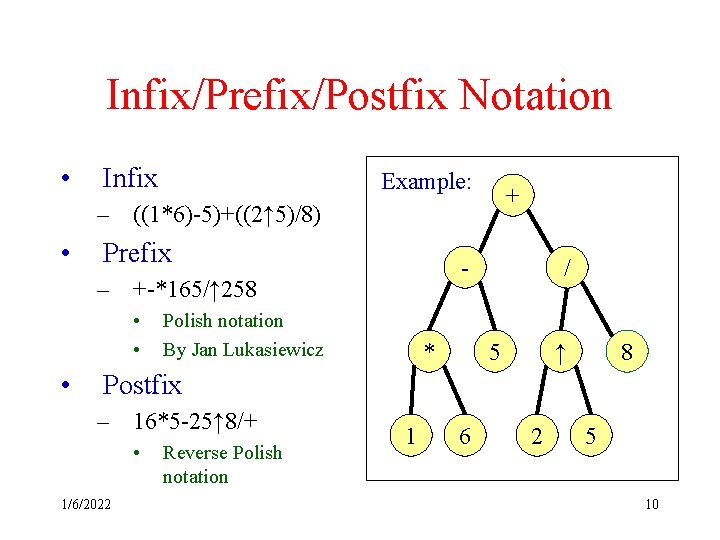
Infix/Prefix/Postfix Notation • Infix Example: + – ((1*6)-5)+((2↑ 5)/8) • Prefix - – +-*165/↑ 258 • • • Polish notation By Jan Lukasiewicz * / 5 ↑ 8 Postfix – 16*5 -25↑ 8/+ • 1/6/2022 Reverse Polish notation 1 6 2 5 10

Class Exercise • Exercise 23. c. (p. 673) – Evaluate and write in infix & postfix forms Each pair of students should use only one sheet of paper while solving the class exercises 1/6/2022 11