ICS 241 Discrete Mathematics II William Albritton Information

ICS 241 • Discrete Mathematics II – William Albritton, Information and Computer Sciences Department at University of Hawai’i at Manoa – For use with Kenneth H. Rosen’s Discrete Mathematics & Its Applications (5 th Edition) – Based on slides originally created by • Dr. Michael P. Frank, Department of Computer & Information Science & Engineering at University of Florida 12/23/2021 1

Section 9. 2: Applications of Trees • Binary search trees – A simple data structure for sorted lists • Decision trees – Minimum comparisons in sorting algorithms • Prefix codes – Huffman coding • Game trees 12/23/2021 2

Binary Search Trees • A representation for sorted sets of items. – Supports the following operations in Θ(log n) average-case time: • Searching for an existing item. • Inserting a new item, if not already present. – Supports printing out all items in Θ(n) time. • Note that inserting into a plain sequence ai would instead take Θ(n) worst-case time. 12/23/2021 3

Binary Search Tree Format • Items are stored at individual tree nodes. • We arrange for the tree to always obey this invariant: Example: 3 – For every item x, • Every node in x’s left subtree is less than x. • Every node in x’s right subtree is greater than x. 12/23/2021 7 1 0 12 5 2 9 8 15 11 4

Recursive Binary Tree Insert procedure insert(T: binary tree, x: item) v : = root[T] if v = null then begin root[T] : = x; return “Done” end else if v = x return “Already present” else if x < v then return insert(left. Subtree[T], x) else {must be x > v} return insert(right. Subtree[T], x) 12/23/2021 5

Class Exercise • Exercise 1. , 3. (p. 656) – Each pair of students should use only one sheet of paper while solving the class exercises 12/23/2021 6

Decision Trees • A decision tree represents a decision-making process. – Each possible “decision point” or situation is represented by a node. – Each possible choice that could be made at that decision point is represented by an edge to a child node. • In the extended decision trees used in decision analysis, we also include nodes that represent random events and their outcomes. 12/23/2021 7

Coin-Weighing Problem • Imagine you have 8 coins, one of which is a lighter counterfeit, and a free-beam balance. – No scale of weight markings is required for this problem! • How many weighings are needed to guarantee that the counterfeit coin will be found? 12/23/2021 ? 8

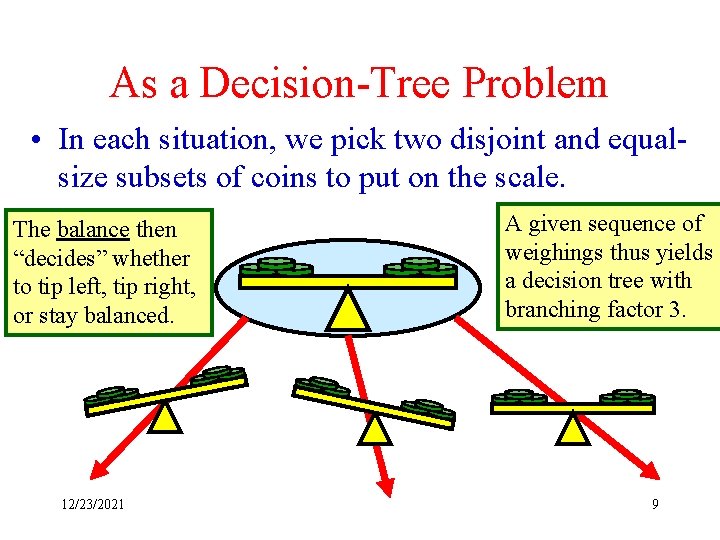
As a Decision-Tree Problem • In each situation, we pick two disjoint and equalsize subsets of coins to put on the scale. The balance then “decides” whether to tip left, tip right, or stay balanced. 12/23/2021 A given sequence of weighings thus yields a decision tree with branching factor 3. 9

Applying the Tree Height Theorem • The decision tree must have at least 8 leaf nodes, since there are 8 possible outcomes. – In terms of which coin is the counterfeit one. • Recall the tree-height theorem, h≥ logm . – Thus the decision tree must have height h ≥ log 38 = 1. 893… = 2. • Let’s see if we solve the problem with only 2 weighings… 12/23/2021 10

General Solution Strategy • The problem is an example of searching for 1 unique particular item, from among a list of n otherwise identical items. – Somewhat analogous to the adage of “searching for a needle in haystack. ” • Armed with our balance, we can attack the problem using a divideand-conquer strategy, like what’s done in binary search. – We want to narrow down the set of possible locations where the desired item (coin) could be found down from n to just 1, in a logarithmic fashion. • Each weighing has 3 possible outcomes. – Thus, we should use it to partition the search space into 3 pieces that are as close to equal-sized as possible. • This strategy will lead to the minimum possible worst-case number of weighings required. 12/23/2021 11

General Balance Strategy • On each step, put n/3 of the n coins to be searched on each side of the scale. – If the scale tips to the left, then: • The lightweight fake is in the right set of n/3 ≈ n/3 coins. – If the scale tips to the right, then: • The lightweight fake is in the left set of n/3 ≈ n/3 coins. – If the scale stays balanced, then: • The fake is in the remaining set of n − 2 n/3 ≈ n/3 coins that were not weighed! • Except if n mod 3 = 1 then we can do a little better by weighing n/3 of the coins on each side. You can prove that this strategy always leads to a balanced 3 -ary tree. 12/23/2021 12

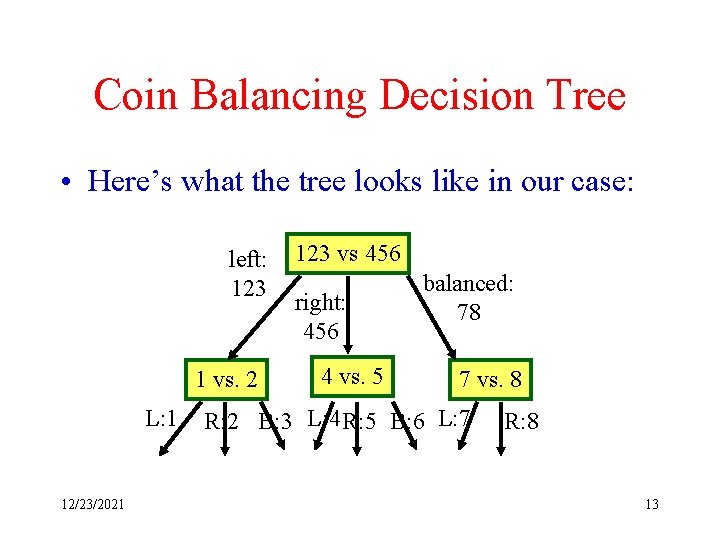
Coin Balancing Decision Tree • Here’s what the tree looks like in our case: left: 123 1 vs. 2 L: 1 12/23/2021 123 vs 456 right: 456 4 vs. 5 balanced: 78 7 vs. 8 R: 2 B: 3 L: 4 R: 5 B: 6 L: 7 R: 8 13

Prefix Codes • A way to encode letters (or any data) using bit strings, so that the bit string for a letter never occurs as the first part of a bit string for another letter – Can be represented as a binary tree, where the characters are the leaves, and the bits correspond to the left and right child • Example: e (0), a(10), t(11), so that 101110 = “ate” • If use 8 -bit ASCII code, then 3*8=24 bits 12/23/2021 14

Class Exercise • Exercise 21. (p. 657) – Each pair of students should use only one sheet of paper while solving the class exercises 12/23/2021 15

Huffman Coding • A way to compress data, using the frequency of symbols in a string to produce a prefix code that encodes the string using the fewest possible bits – Tree is built from the bottom-up, connecting the symbols and nodes with the lowest frequencies first • Parent = frequency of left child + freq. of right child • Left child frequency > right child frequency 12/23/2021 16

Huffman Coding Example • Letters & respective frequencies – A: 0. 08, B: 0. 10, C: 0. 12, D: 0. 15, E: 0. 20, F: 0. 35 • Huffman coding gives following encodings – A(111), B(110), C(011), D(010), E(10), F(00) • Average number of bits used to encode a letter – 3*0. 08 + 3* 0. 10 + 3*0. 12 + 3*0. 15 + 2*0. 20 + 2*0. 35 = 2. 45 12/23/2021 17

Class Exercise • Exercise 23. (p. 657) – Each pair of students should use only one sheet of paper while solving the class exercises 12/23/2021 18

Game Trees • Game of Nim – Two players remove 1 or more stones from one of the piles of stones • Lose by removing the last stone – Represent game with a tree that shows all possible moves in the game • Root is start • Even level nodes are boxes (1 st player’s move) • Odd level nodes are circles(2 nd player’s move) 12/23/2021 19

Game of Nim • Determine who will win by minmax strategy – Leaves are given numbers that correspond to who wins the game • +1 if 1 st player wins • -1 if 2 nd player wins – For each node, take the maximum (for 1 st player) or minimum value of children (for 2 nd player) – 1 st player tries to maximize payoffs & 2 nd player tries to minimize payoffs 12/23/2021 20

Game of Nim Example • Start with 3 piles of stones: 2, 2, & 1 stones – Start with square node (1 st player’s move) – 3 children are circular nodes (2 nd player’s move) – Leaves are +1/-1 for 1 st/2 nd player wins – Take min or max values of children to determine who will win the game 12/23/2021 21

Class Exercise • Exercise 33. (p. 659) – Each pair of students should use only one sheet of paper while solving the class exercises 12/23/2021 22