IB Physics Oscillations and Waves The 5 Properties

IB Physics Oscillations and Waves

The 5 Properties of Waves Rectilinear Propagation: waves propagate (move or spread out) in straight lines in all directions away from the source. ( s = v∙t ) Reflection: change in direction of a wave at an interface between two different media so that the wave returns into the medium from which it originated. ( m ∠i = m∠r ) Refraction: change in direction of a wave due to a change in its speed. Observed when a wave passes from one medium to another. (Snell’s law. )

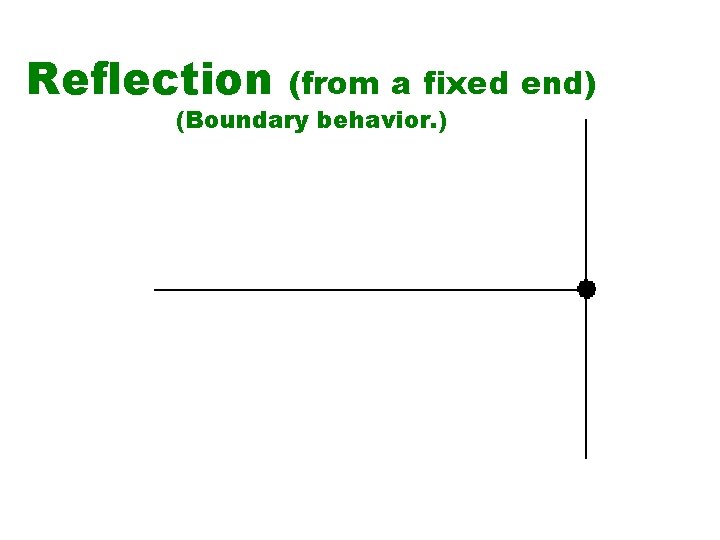
Reflection (from a fixed end) (Boundary behavior. )

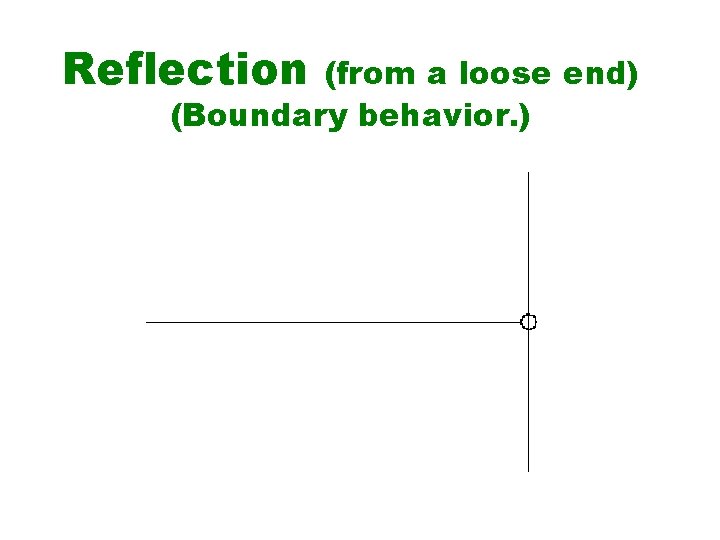
Reflection (from a loose end) (Boundary behavior. )

The 5 Properties of Waves (con’t. ) Diffraction: bending of waves around small obstacles and the spreading out of waves passing through small openings. Interference: the addition (superposition) of two or more waves that results in a new wave pattern.

Any Wave: is a traveling disturbance that carries energy. Two types of waves: 1) Transverse – the disturbance is perpendicular to the direction the wave is traveling 2) Longitudinal – the disturbance is parallel to the direction the wave is traveling

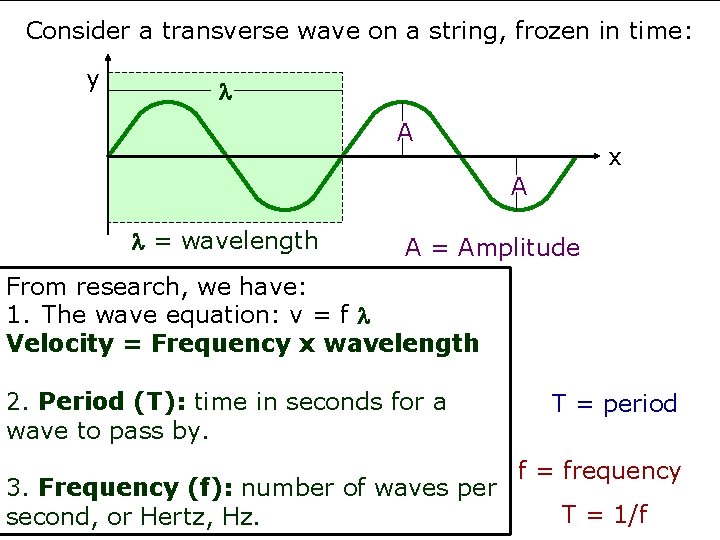
Consider a transverse wave on a string, frozen in time: y A x A = wavelength A = Amplitude From research, we have: 1. The wave equation: v = f Velocity = Frequency x wavelength 2. Period (T): time in seconds for a wave to pass by. 3. Frequency (f): number of waves per second, or Hertz, Hz. T = period f = frequency T = 1/f

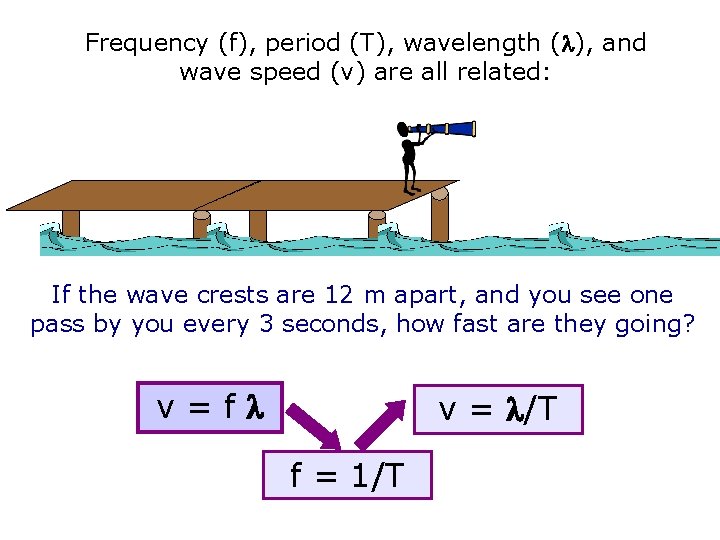
Frequency (f), period (T), wavelength ( ), and wave speed (v) are all related: If the wave crests are 12 m apart, and you see one pass by you every 3 seconds, how fast are they going? v=f v = /T f = 1/T

Ex: Radio Waves 2. 81 m How long do you think the wavelengths of radio waves are ? Radio waves are a type of Electromagnetic Wave Radio waves travel at the speed of light in a vacuum, 3. 00 x 108 m/s. Find the wavelength of radio waves from station 106. 7 M Hz.

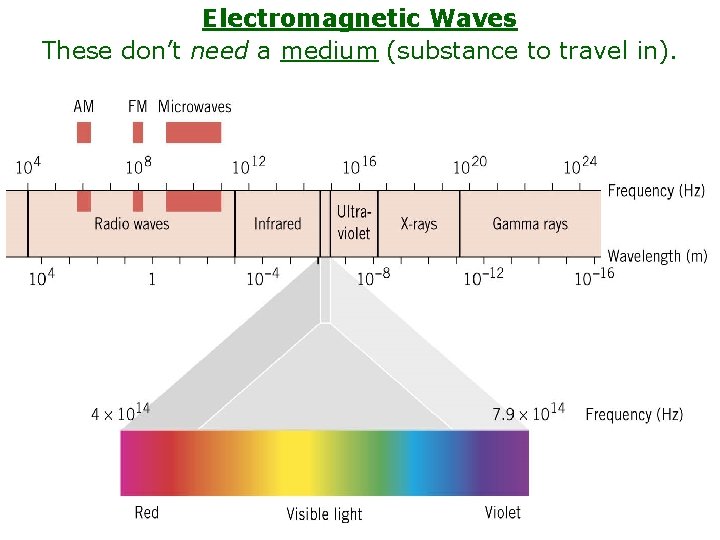
Electromagnetic Waves These don’t need a medium (substance to travel in).

All other waves require a medium (air, water, string, etc. ) The speed of a wave depends on the medium. v=f That means that these two are inversely proportional f f

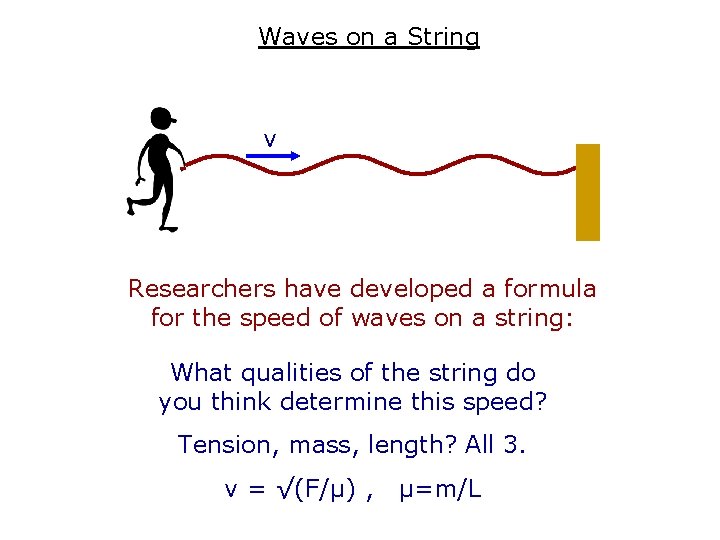
Waves on a String v Researchers have developed a formula for the speed of waves on a string: What qualities of the string do you think determine this speed? Tension, mass, length? All 3. v = √(F/µ) , µ=m/L

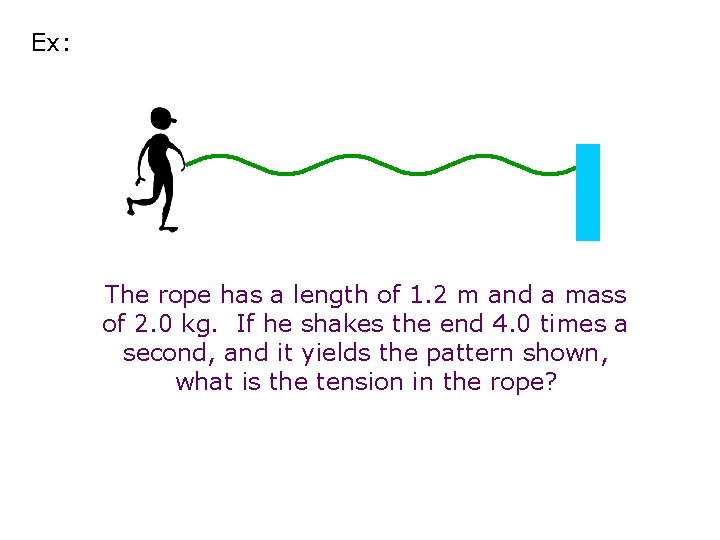
Ex: The rope has a length of 1. 2 m and a mass of 2. 0 kg. If he shakes the end 4. 0 times a second, and it yields the pattern shown, what is the tension in the rope?

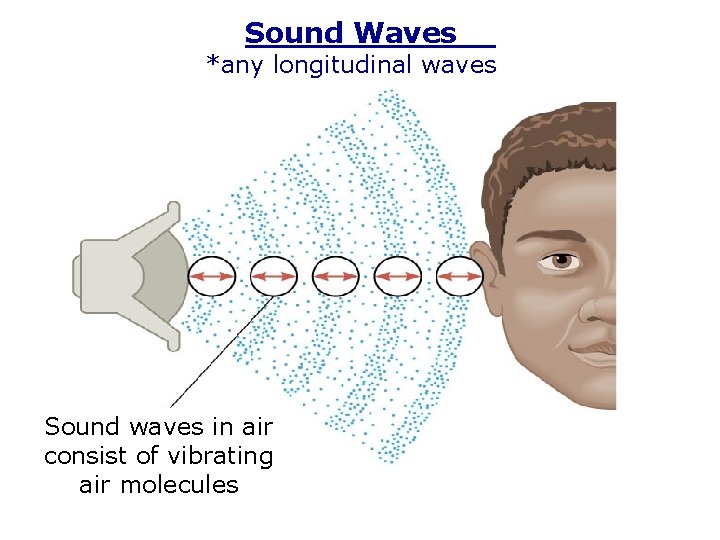
Sound Waves *any longitudinal waves Sound waves in air consist of vibrating air molecules

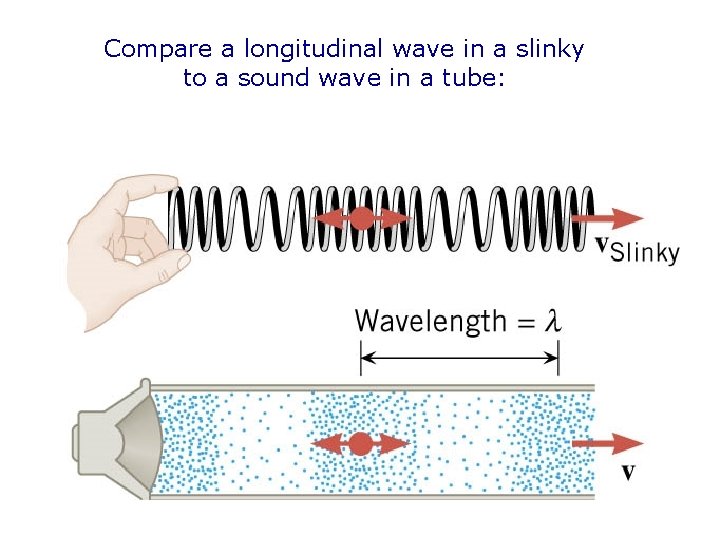
Compare a longitudinal wave in a slinky to a sound wave in a tube:

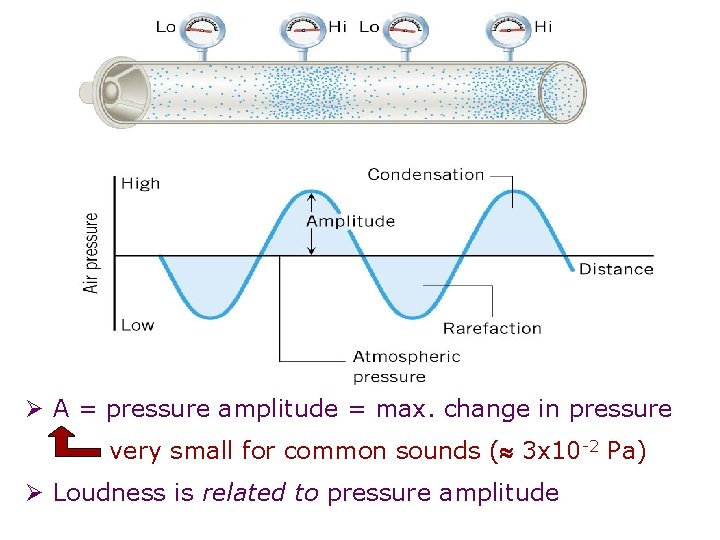
Ø A = pressure amplitude = max. change in pressure very small for common sounds ( 3 x 10 -2 Pa) Ø Loudness is related to pressure amplitude

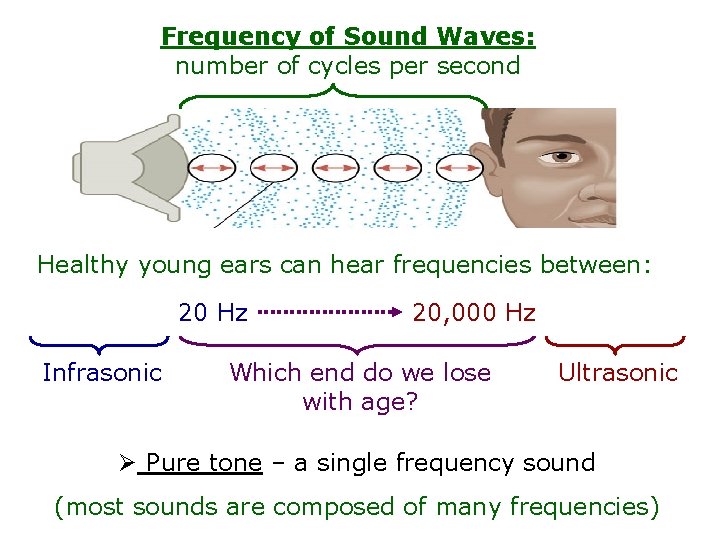
Frequency of Sound Waves: number of cycles per second Healthy young ears can hear frequencies between: 20 Hz Infrasonic 20, 000 Hz Which end do we lose with age? Ultrasonic Ø Pure tone – a single frequency sound (most sounds are composed of many frequencies)

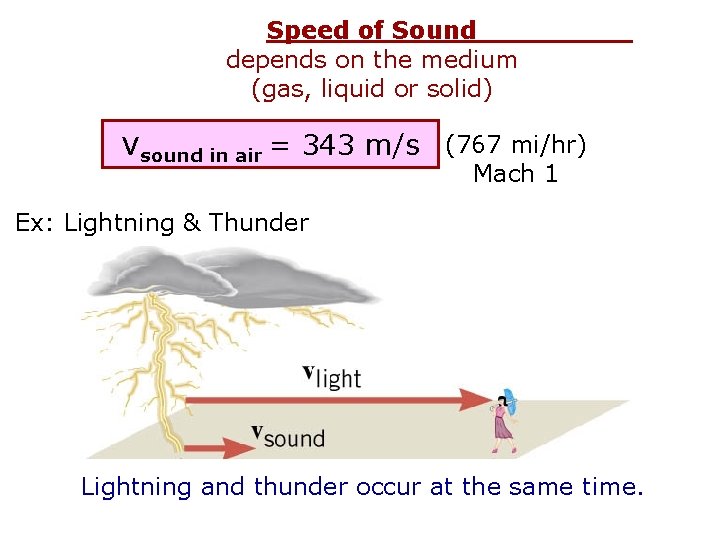
Speed of Sound depends on the medium (gas, liquid or solid) vsound in air = 343 m/s (767 mi/hr) Mach 1 Ex: Lightning & Thunder Lightning and thunder occur at the same time.

Speed of sound in an ideal gas k = 1. 38 x 10 -23 J/K (Boltzmann const. ) T = Kelvin temperature m = molecular mass in kg = CP/CV (the Adiabatic constant) For air (mostly O₂ and N₂), = 1. 40

Ex: Verify the speed of sound in 20. 0⁰C air if the average air molecule mass is 28. 9 u, and = 1. 40 for air.

Speed of sound in a liquid Bulk Modulus (adiabatic) Density of the liquid. Water? Ex: Water, Bad ≈2. 25 G Pa , increases with pressure 9 The speed of sound in water is around _____ m/s (that’s over __ times as fast as it travels in air!)

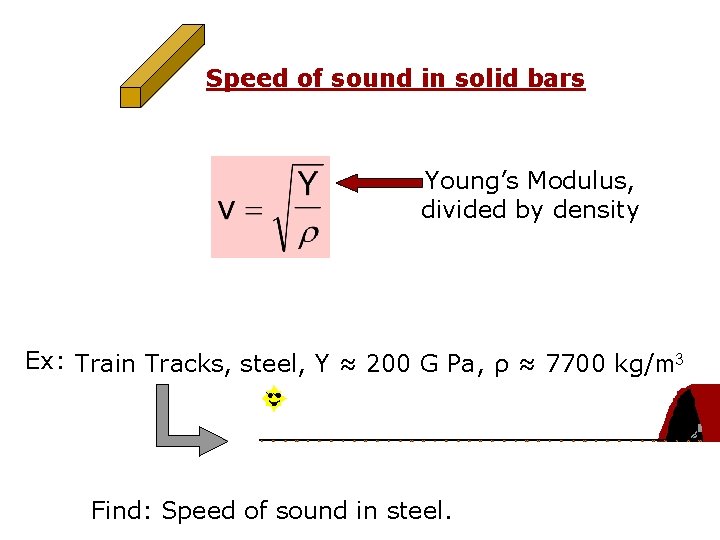
Speed of sound in solid bars Young’s Modulus, divided by density Ex: Train Tracks, steel, Y ≈ 200 G Pa, ρ ≈ 7700 kg/m 3 Find: Speed of sound in steel.

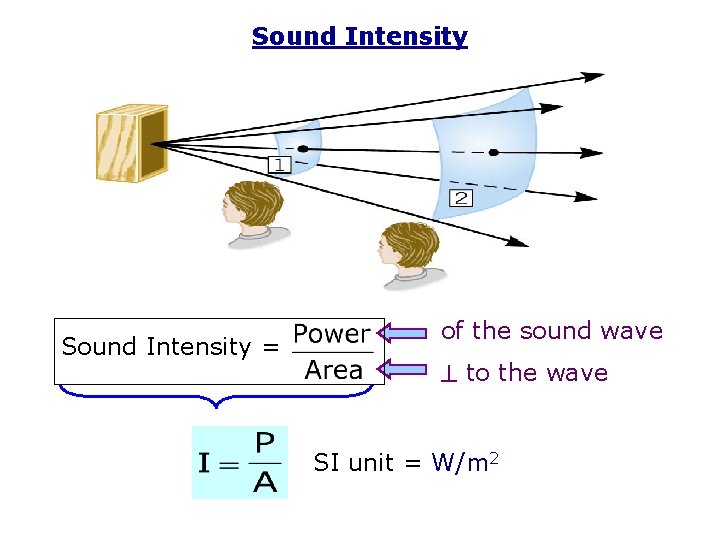
Sound Intensity = of the sound wave to the wave SI unit = W/m 2

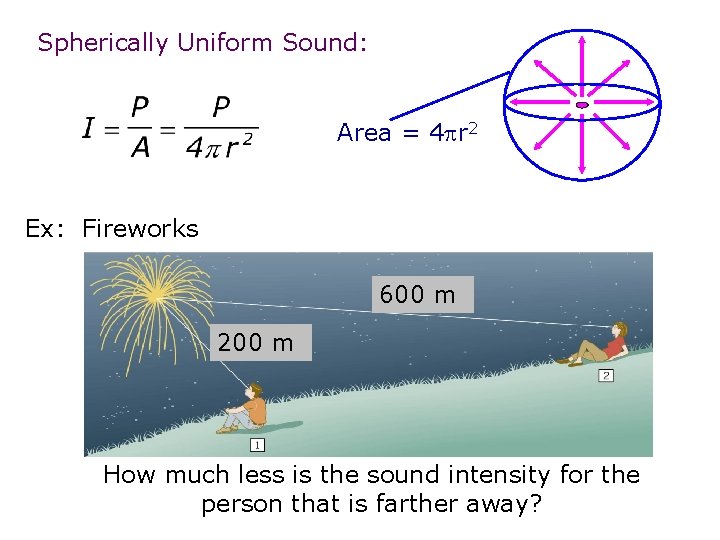
Spherically Uniform Sound: Area = 4 r 2 Ex: Fireworks 600 m 200 m How much less is the sound intensity for the person that is farther away?

Notes on Sound Intensity Ø Intensity is related to loudness (but not directly proportional) Ø 10 -12 W/m 2 = lower threshold of human hearing Ø 1 W/m 2 = enough to cause ear damage Ø Different sound intensities are compared using: decibels (d. B) To compare two intensities (I and I 0): (in decibels) = 10 log (I/I 0) “Intensity Level” (unitless) For sound meters, I 0= threshold = 10 -12 W/m 2

Ex: If a sound meter picks up an intensity of 1. 0 x 10 -5 W/m 2 , what will be the intensity level reading in d. B?

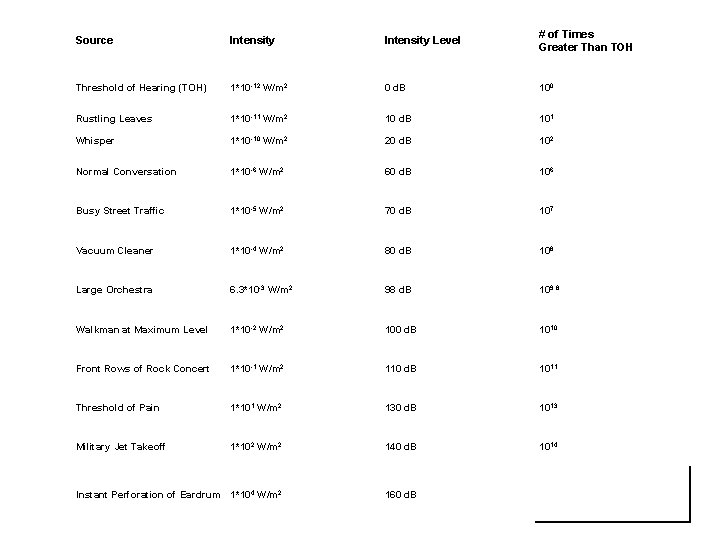
Source Intensity Level # of Times Greater Than TOH Threshold of Hearing (TOH) 1*10 -12 W/m 2 0 d. B 100 Rustling Leaves 1*10 -11 W/m 2 10 d. B 101 Whisper 1*10 -10 W/m 2 20 d. B 102 Normal Conversation 1*10 -6 W/m 2 60 d. B 106 Busy Street Traffic 1*10 -5 W/m 2 70 d. B 107 Vacuum Cleaner 1*10 -4 W/m 2 80 d. B 108 Large Orchestra 6. 3*10 -3 W/m 2 98 d. B 109. 8 Walkman at Maximum Level 1*10 -2 W/m 2 100 d. B 1010 Front Rows of Rock Concert 1*10 -1 W/m 2 110 d. B 1011 Threshold of Pain 1*101 W/m 2 130 d. B 1013 Military Jet Takeoff 1*102 W/m 2 140 d. B 1014 Instant Perforation of Eardrum 1*104 W/m 2 160 d. B

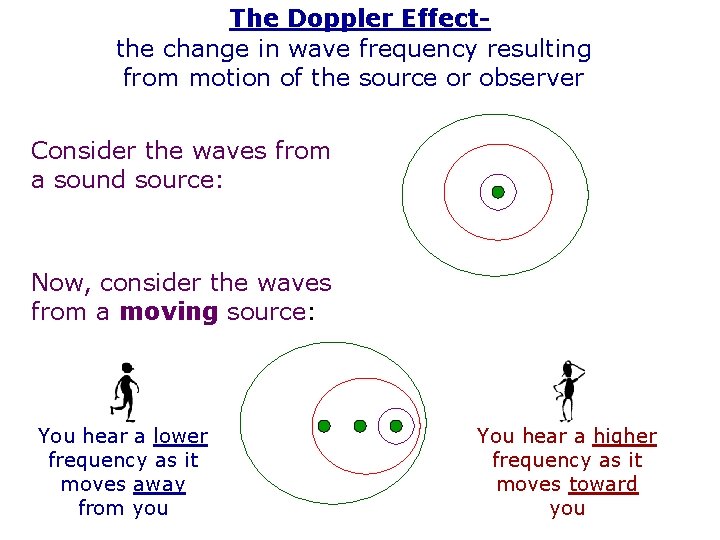
The Doppler Effectthe change in wave frequency resulting from motion of the source or observer Consider the waves from a sound source: Now, consider the waves from a moving source: You hear a lower frequency as it moves away from you You hear a higher frequency as it moves toward you

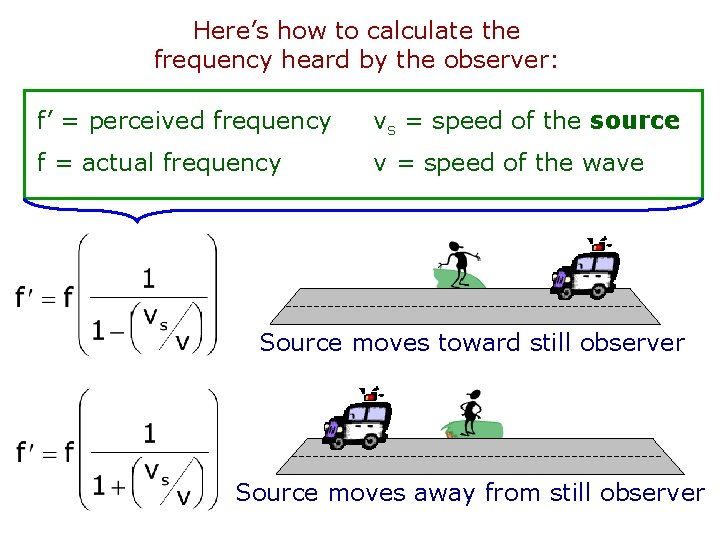
Here’s how to calculate the frequency heard by the observer: f’ = perceived frequency vs = speed of the source f = actual frequency v = speed of the wave Source moves toward still observer Source moves away from still observer

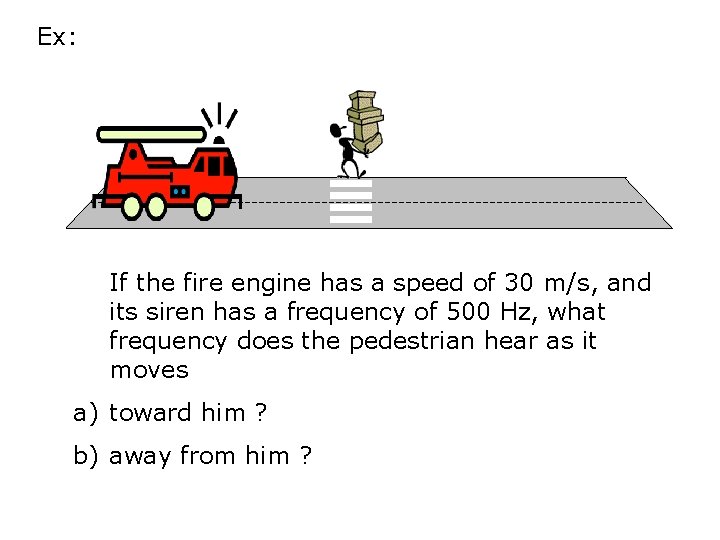
Ex: If the fire engine has a speed of 30 m/s, and its siren has a frequency of 500 Hz, what frequency does the pedestrian hear as it moves a) toward him ? b) away from him ?

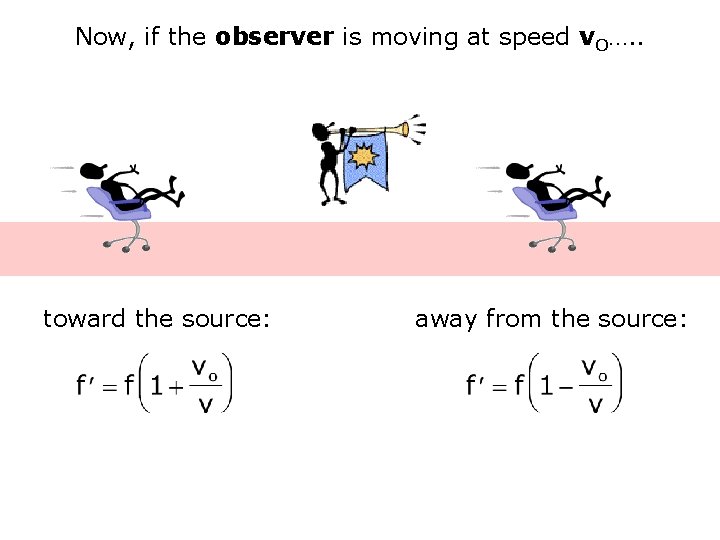
Now, if the observer is moving at speed v. O…. . toward the source: away from the source:

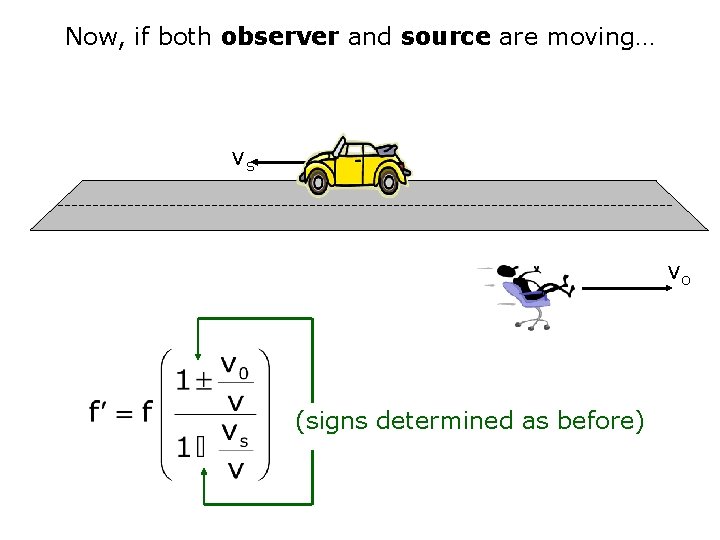
Now, if both observer and source are moving… vs vo (signs determined as before)

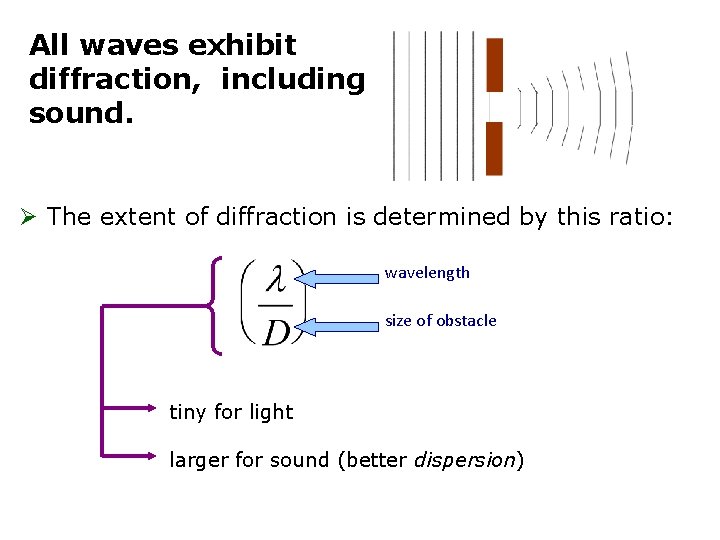
All waves exhibit diffraction, including sound. Ø The extent of diffraction is determined by this ratio: wavelength size of obstacle tiny for light larger for sound (better dispersion)

Diffraction of Sound Waves For a single slit (or doorway) of width D : D Angle of 1 st diffraction minimum For a circular opening of diameter D : D Angle of 1 st diffraction minimum

Beat Frequency Refers to the rate at which the volume is heard to be oscillating from high to low volume. The beat frequency is always equal to the difference in frequency of the two notes that interfere to produce the beats. fbeat = f 1 – f 2 So, with frequencies of 256 Hz and 254 Hz, a beat frequency of 2 Hz will be detected.

Standing Waves in Open and Closed Tubes: (Based on Resonance) closed: /4, 3 /4, 5 /4, … odd. mult. open: /2, , 3 /2, 2 , … all mult.

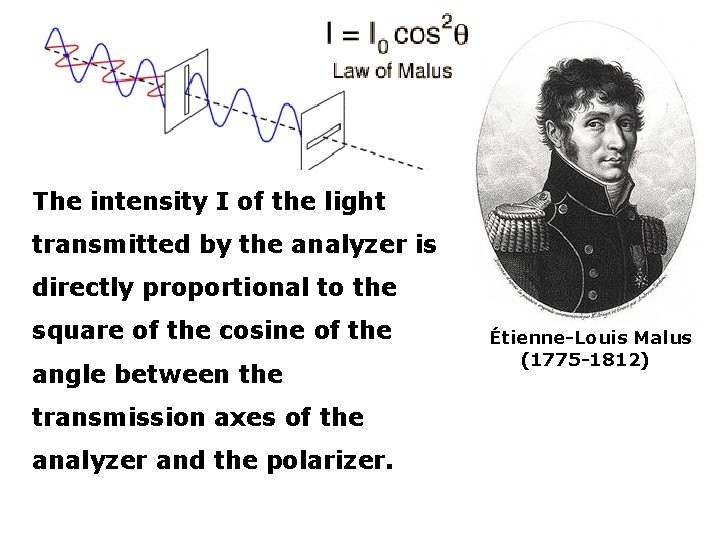
The intensity I of the light transmitted by the analyzer is directly proportional to the square of the cosine of the angle between the transmission axes of the analyzer and the polarizer. Étienne-Louis Malus (1775 -1812)

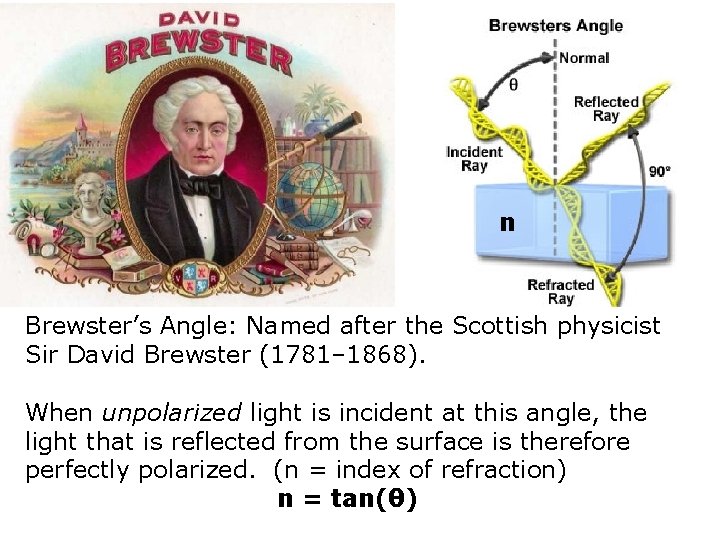
n Brewster’s Angle: Named after the Scottish physicist Sir David Brewster (1781– 1868). When unpolarized light is incident at this angle, the light that is reflected from the surface is therefore perfectly polarized. (n = index of refraction) n = tan(θ)

OSCILLATIONS AND WAVES: Equations and constants. s = v∙t m ∠i = m∠r v=f f = 1/T Ve/m waves, v = 3. 00 x 108 m/s vwave in string, v = √(F/µ) µ=m/L vsound in ideal gas, k = 1. 38 x 10 -23 J/K m = molecular mass, 1. 67 x 10 -27 kg = c. P/c. V (Adiabatic constant) For air (mostly O₂ and N₂), = 1. 40 vsound in air = 331. 5 m/s @ 0. 0 °C, +. 6 (m/s)/°C vsound in liquid, vsound in solid, (in decibels) = 10 log (I/I 0) toward away I 0= 1. 0 x 10 -12 W/m 2 I = P/4πr 2 fbeat = f 1 – f 2 n = tan(θ) I = I 0 cos 2(θ) closed: /4, 3 /4, 5 /4, … odd. mult. open: /2, , 3 /2, 2 , … all mult.