IAT 355 Clustering SCHOOL OF INTERACTIVE ARTS TECHNOLOGY

IAT 355 Clustering ___________________________________________ SCHOOL OF INTERACTIVE ARTS + TECHNOLOGY [SIAT] | WWW. SIAT. SFU. CA IAT 355 1 1

Lecture outline • Distance/Similarity between data objects • Data objects as geometric data points • Clustering problems and algorithms – K-means – K-median

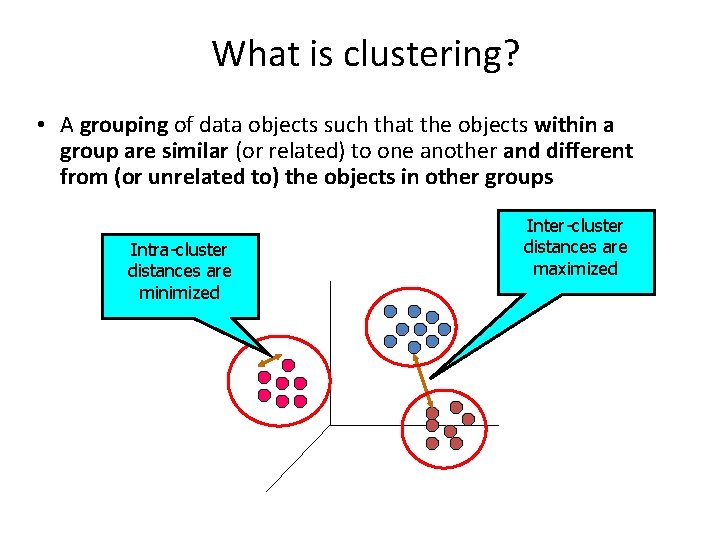
What is clustering? • A grouping of data objects such that the objects within a group are similar (or related) to one another and different from (or unrelated to) the objects in other groups Intra-cluster distances are minimized Inter-cluster distances are maximized

Outliers • Outliers are objects that do not belong to any cluster or form clusters of very small cardinality cluster outliers • In some applications we are interested in discovering outliers, not clusters (outlier analysis)

What is clustering? • Clustering: the process of grouping a set of objects into classes of similar objects – Documents within a cluster should be similar. – Documents from different clusters should be dissimilar. • The commonest form of unsupervised learning • Unsupervised learning = learning from raw data, as opposed to supervised data where a classification of examples is given – A common and important task that finds many applications in Info Retrieval and other places

Why do we cluster? • Clustering : given a collection of data objects group them so that – Similar to one another within the same cluster – Dissimilar to the objects in other clusters • Clustering results are used: – As a stand-alone tool to get insight into data distribution • Visualization of clusters may unveil important information – As a preprocessing step for other algorithms • Efficient indexing or compression often relies on clustering

Applications of clustering? • Image Processing – cluster images based on their visual content • Web – Cluster groups of users based on their access patterns on webpages – Cluster webpages based on their content • Bioinformatics – Cluster similar proteins together (similarity wrt chemical structure and/or functionality etc) • Many more…

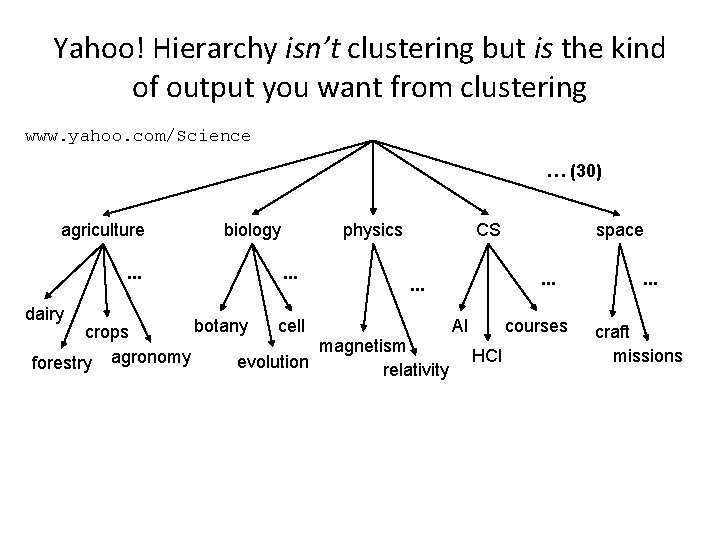
Yahoo! Hierarchy isn’t clustering but is the kind of output you want from clustering www. yahoo. com/Science … (30) agriculture. . . dairy biology physics. . . CS. . . space. . . botany cell AI courses crops magnetism HCI agronomy evolution forestry relativity . . . craft missions

The clustering task • Group observations into groups so that the observations belonging in the same group are similar, whereas observations in different groups are different • Basic questions: – What does “similar” mean – What is a good partition of the objects? I. e. , how is the quality of a solution measured – How to find a good partition of the observations

Observations to cluster • Real-value attributes/variables – e. g. , salary, height • Binary attributes – e. g. , gender (M/F), has_cancer(T/F) • Nominal (categorical) attributes – e. g. , religion (Christian, Muslim, Buddhist, Hindu, etc. ) • Ordinal/Ranked attributes – e. g. , military rank (soldier, sergeant, lutenant, captain, etc. ) • Variables of mixed types – multiple attributes with various types

Observations to cluster • Usually data objects consist of a set of attributes (also known as dimensions) • J. Smith, 200 K • If all d dimensions are real-valued then we can visualize each data point as points in a d-dimensional space • If all d dimensions are binary then we can think of each data point as a binary vector

Distance functions • The distance d(x, y) between two objects xand y is a metric if – – d(i, j) 0 (non-negativity) d(i, i)=0 (isolation) d(i, j)= d(j, i) (symmetry) d(i, j) ≤ d(i, h)+d(h, j) (triangular inequality) [Why do we need it? ] • The definitions of distance functions are usually different for real, boolean, categorical, and ordinal variables. • Weights may be associated with different variables based on applications and data semantics.

• data matrix attributes/dimensions Data Cases/Objects Data Structures objects • Distance matrix

Distance functions for binary vectors • Jaccard similarity between binary vectors X and Y • Jaccard distance between binary vectors X and Y Jdist(X, Y) = 1 - JSim(X, Y) • Example: • JSim = 1/6 • Jdist = 5/6 Q 1 Q 2 Q 3 Q 4 Q 5 Q 6 X 1 0 0 1 1 1 Y 0 1 1 0

Distance functions for real-valued vectors • Lp norms or Minkowski distance: where p is a positive integer • If p = 1, L 1 is the Manhattan (or city block) distance:

Distance functions for real-valued vectors • If p = 2, L 2 is the Euclidean distance: • Also one can use weighted distance: • Very often Lpp is used instead of Lp (why? )

Partitioning algorithms: basic concept • Construct a partition of a set of n objects into a set of k clusters – Each object belongs to exactly one cluster – The number of clusters k is given in advance

The k-means problem • Given a set X of n points in a d-dimensional space and an integer k • Task: choose a set of k points {c 1, c 2, …, ck} in the d-dimensional space to form clusters {C 1, C 2, …, Ck} such that is minimized • Some special cases: k = 1, k = n

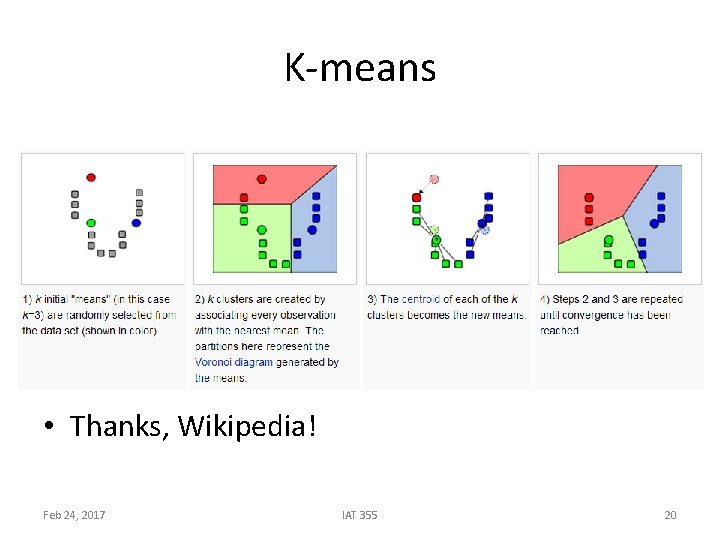
The k-means algorithm • One way of solving the k-means problem • Randomly pick k cluster centers {c 1, …, ck} • For each i, set the cluster Ci to be the set of points in X that are closer to ci than they are to cj for all i≠j • For each i let ci be the center of cluster Ci (mean of the vectors in Ci) • Repeat until convergence

K-means • Thanks, Wikipedia! Feb 24, 2017 IAT 355 20

Properties of the k-means algorithm • Finds a local optimum • Converges often quickly (but not always) • The choice of initial points can have large influence in the result

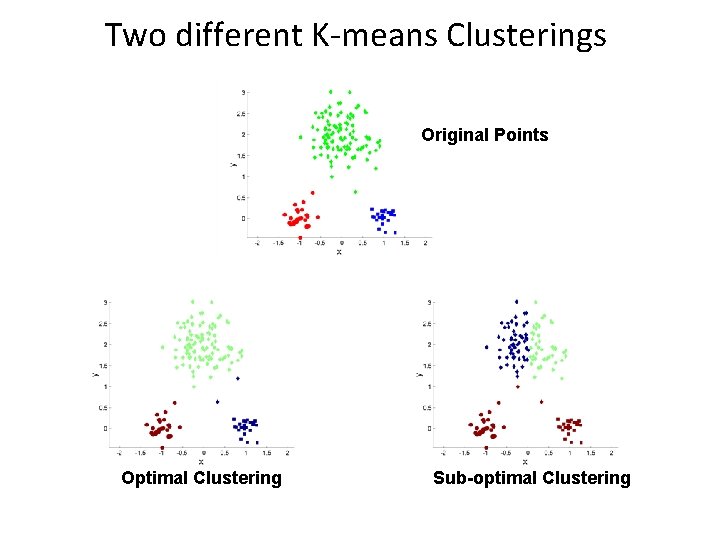
Two different K-means Clusterings Original Points Optimal Clustering Sub-optimal Clustering

Discussion k-means algorithm • Finds a local optimum • Converges often quickly (but not always) • The choice of initial points can have large influence – Clusters of different densities – Clusters of different sizes • Outliers can also cause a problem (Example? )

Some alternatives to random initialization of the central points • Multiple runs – Helps, but probability is not on your side • Select original set of points by methods other than random. E. g. , pick the most distant (from each other) points as cluster centers (kmeans++ algorithm)

The k-median problem • Given a set X of n points in a d-dimensional space and an integer k • Task: choose a set of k points {c 1, c 2, …, ck} from X and form clusters {C 1, C 2, …, Ck} such that is minimized

k-means vs k-median • k-Means: Choose arbitrary cluster centers ci • k-Medians: • Task: choose a set of k points {c 1, c 2, …, ck} from X and form clusters {C 1, C 2, …, Ck} such that

Text: Notion of similarity/distance • Ideal: semantic similarity. • Practical: term-statistical similarity – We will use cosine similarity. – Docs as vectors. – For many algorithms, easier to think in terms of a distance (rather than similarity) between docs. – We will mostly speak of Euclidean distance • But real implementations use cosine similarity

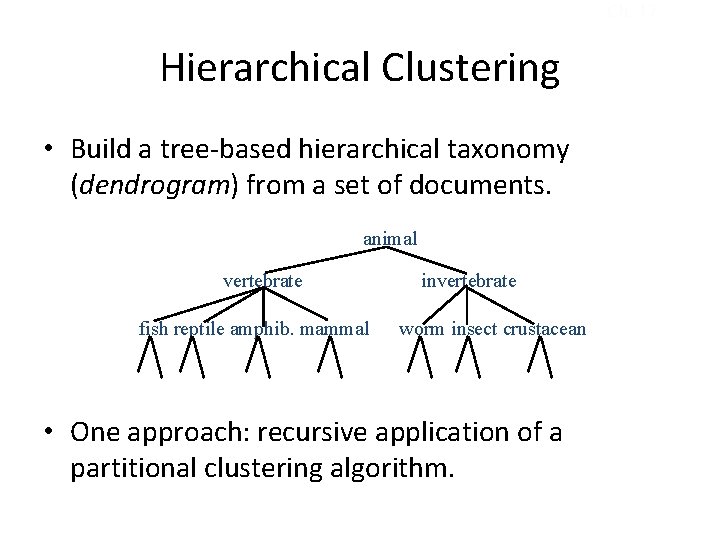
Ch. 17 Hierarchical Clustering • Build a tree-based hierarchical taxonomy (dendrogram) from a set of documents. animal vertebrate fish reptile amphib. mammal invertebrate worm insect crustacean • One approach: recursive application of a partitional clustering algorithm.

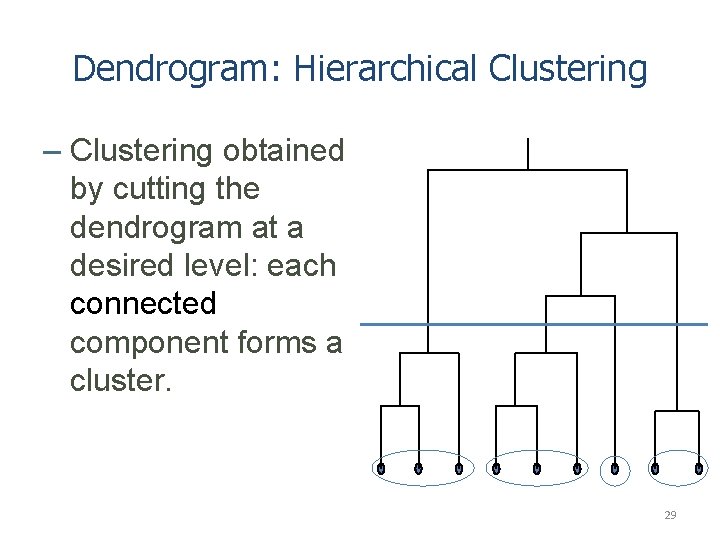
Dendrogram: Hierarchical Clustering – Clustering obtained by cutting the dendrogram at a desired level: each connected component forms a cluster. 29

Hierarchical Agglomerative Clustering (HAC) Sec. 17. 1 • Starts with each item in a separate cluster – then repeatedly joins the closest pair of clusters, until there is only one cluster. • The history of merging forms a binary tree or hierarchy. Note: the resulting clusters are still “hard” and induce a partition

Sec. 17. 2 Closest pair of clusters • Many variants to defining closest pair of clusters • Single-link – Similarity of the most similar (single-link) • Complete-link – Similarity of the “furthest” points, the least similar • Centroid – Clusters whose centroids (centers of gravity) are the most similar • Average-link – Average distance between pairs of elements

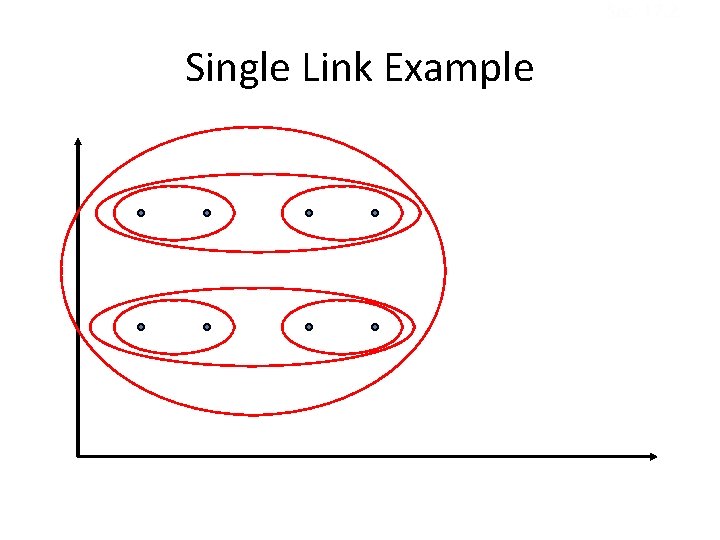
Single Link Agglomerative Clustering • Use maximum similarity of pairs: • Can result in long and thin clusters due to chaining effect. • After merging ci and cj, the similarity of the resulting cluster to another cluster, ck, is: Sec. 17. 2

Sec. 17. 2 Single Link Example

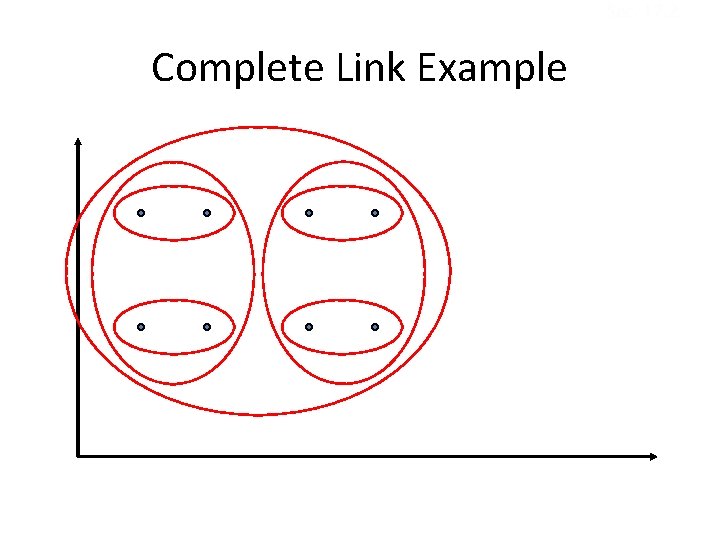
Sec. 17. 2 Complete Link • Use minimum similarity of pairs: • Makes “tighter, ” spherical clusters that are typically preferable. • After merging ci and cj, the similarity of the resulting cluster to another cluster, ck, is: Ci Cj Ck

Sec. 17. 2 Complete Link Example

Sec. 16. 3 What Is A Good Clustering? • Internal criterion: A good clustering will produce high quality clusters in which: – the intra-class (that is, within-cluster) similarity is high – the inter-class (between clusters) similarity is low – The measured quality of a clustering depends on both the item (document) representation and the similarity measure used

Sec. 16. 3 External criteria for clustering quality • Quality measured by its ability to discover some or all of the hidden patterns or latent classes in gold standard data • Assesses a clustering with respect to ground truth … requires labeled data • Assume documents with C gold standard classes, while our clustering algorithms produce K clusters, ω1, ω2, …, ωK with ni members.

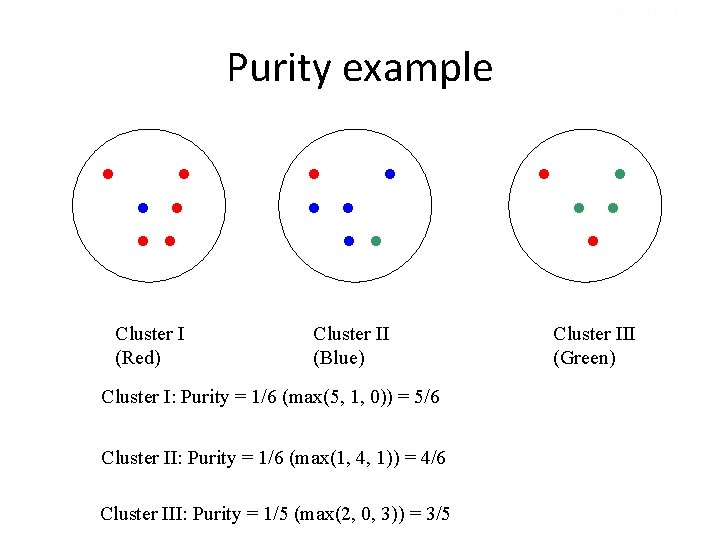
Purity • Simple measure: purity, the ratio between the most common class in the cluster πi and the size of cluster ωi • Biased because having n clusters maximizes purity • Others are entropy of classes in clusters (or mutual information between classes and clusters)

Sec. 16. 3 Purity example Cluster I (Red) Cluster II (Blue) Cluster I: Purity = 1/6 (max(5, 1, 0)) = 5/6 Cluster II: Purity = 1/6 (max(1, 4, 1)) = 4/6 Cluster III: Purity = 1/5 (max(2, 0, 3)) = 3/5 Cluster III (Green)

Sec. 16. 3 Rand Index measures between pair decisions. Here RI = 0. 68 Number of points Same Cluster in clustering Different Clusters in clustering Same class in ground truth 20 24 Different classes in ground truth 20 72

Sec. 16. 3 Rand index

Thanks to: • Evimaria Terzi, Boston University • Pandu Nayak and Prabhakar Raghavan, Stanford University