IAPT Workshop 2 nd August ISP CUSAT V
































- Slides: 64

IAPT Workshop 2 nd August ISP, CUSAT V P N Nampoori nampoori@gmail. com

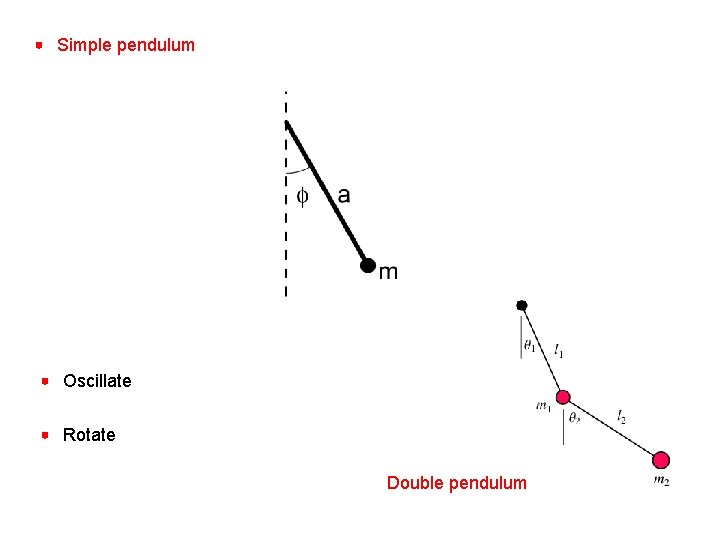
Simple pendulum Oscillate Rotate

Simple pendulum Oscillate Rotate Double pendulum



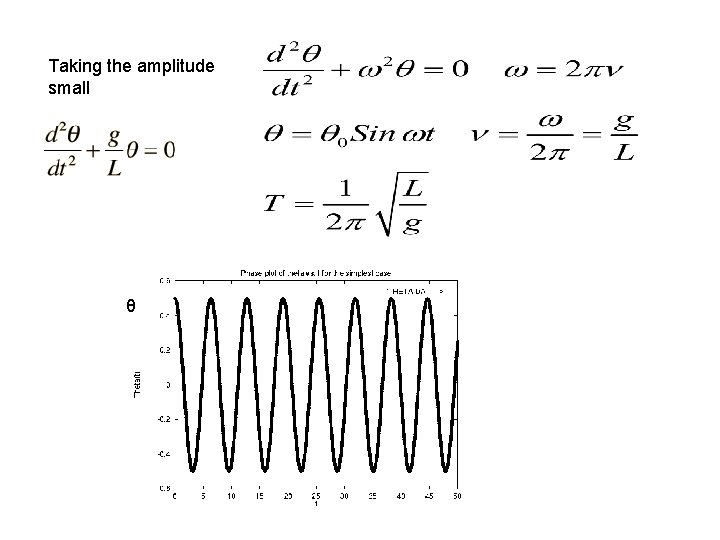
Taking the amplitude small θ

The hallmark of linear equations. We can predict state of the simple pendulum at any future time Linearlty helps us to predict future.


Alternate representation of damped motion of simple pendulum Phase space plot

Second order nonlinear differential equation Superposition principle is not valid Prediction is not possible

Linear dynamics – prediction possible

Traffic jam –Nonlinear dynamics - prediction is impossible

One-dimensional maps, definition: - a set V (e. g. real numbers between 0 and 1) - a map of the kind f: V V Linear maps: - a and b are constants - linear maps are invertible with no ambiguity Non-linear maps: The logistic map

One-dimensional maps Non-linear maps: The logistic map with Motivation: Discretization of the logistic equation for the dynamics of a biological population x b: birth rate (assumed constant) cx: death rate depends on population (competition for food, …) How do we explore the logistic map?

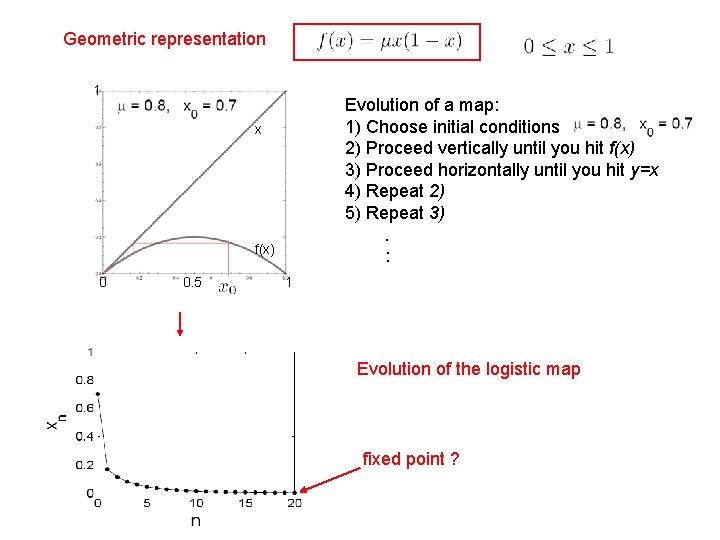
Geometric representation 1 Evolution of a map: 1) Choose initial conditions 2) Proceed vertically until you hit f(x) 3) Proceed horizontally until you hit y=x 4) Repeat 2) 5) Repeat 3). : x f(x) 0 0. 5 1 Evolution of the logistic map fixed point ?

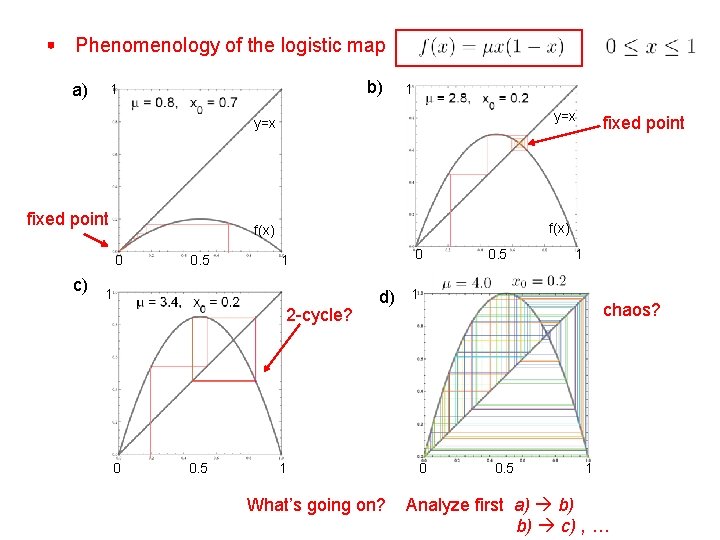
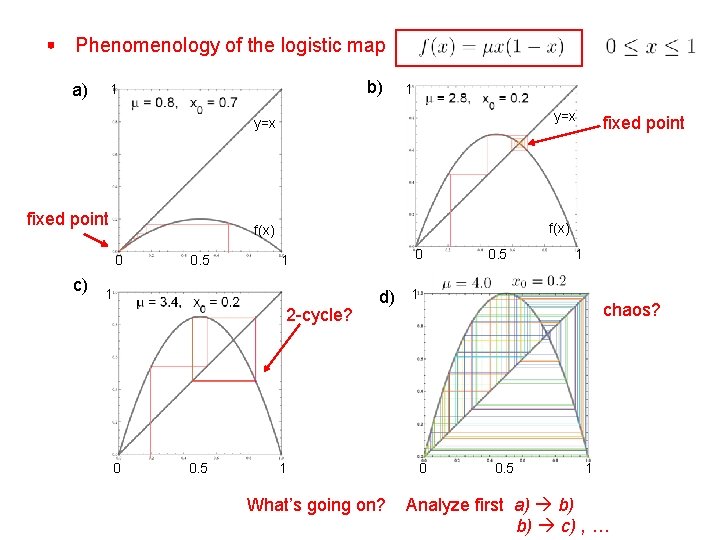
Phenomenology of the logistic map a) b) 1 1 y=x fixed point c) f(x) 0 0. 5 2 -cycle? 0. 5 0 1 1 0 fixed point d) 1 What’s going on? 0. 5 1 1 chaos? 0 0. 5 1 Analyze first a) b) b) c) , …

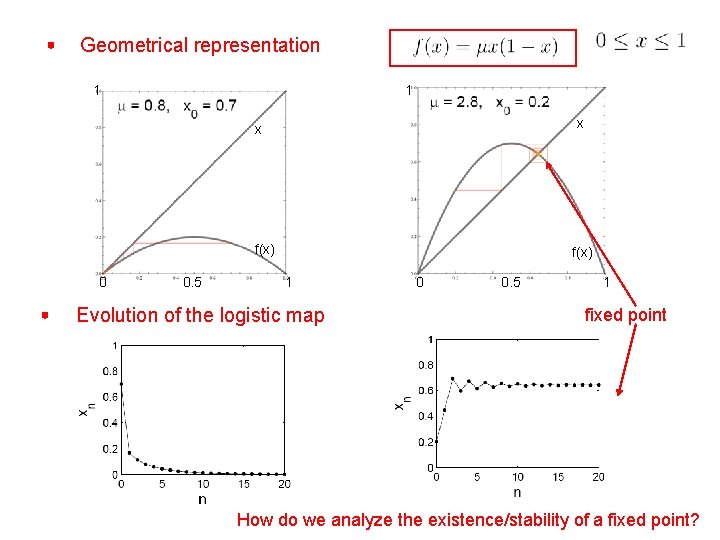
Geometrical representation 1 1 x x f(x) 0 0. 5 f(x) 1 Evolution of the logistic map 0 0. 5 1 fixed point How do we analyze the existence/stability of a fixed point?


Fixed points - Condition for existence: - Logistic map: - Notice: since the second fixed point exists only for Stability - Define the distance of from the fixed point Taylor expansion - Consider a neighborhood of - The requirement implies Logistic map?

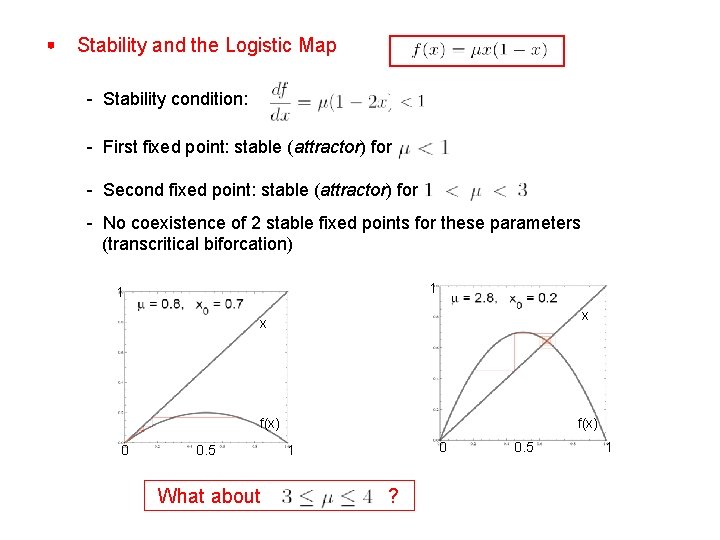
Stability and the Logistic Map - Stability condition: - First fixed point: stable (attractor) for - Second fixed point: stable (attractor) for - No coexistence of 2 stable fixed points for these parameters (transcritical biforcation) 1 1 x x f(x) 0 0. 5 What about f(x) 0 1 ? 0. 5 1

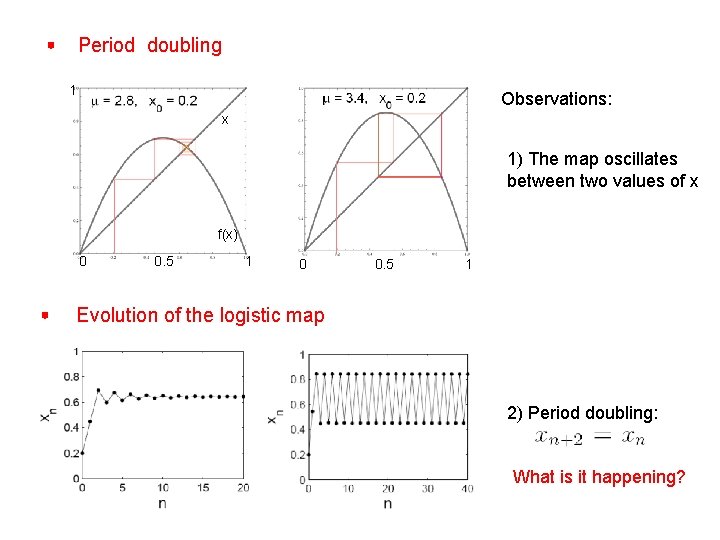
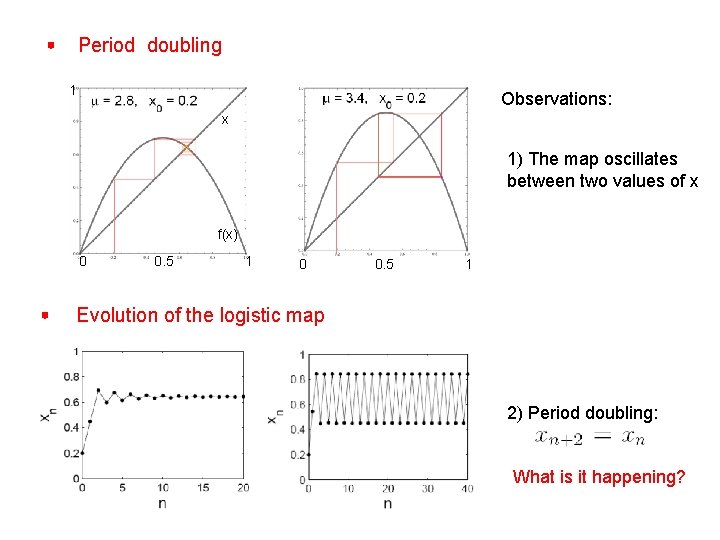
Period doubling 1 Observations: x 1) The map oscillates between two values of x f(x) 0 0. 5 1 Evolution of the logistic map 2) Period doubling: What is it happening?

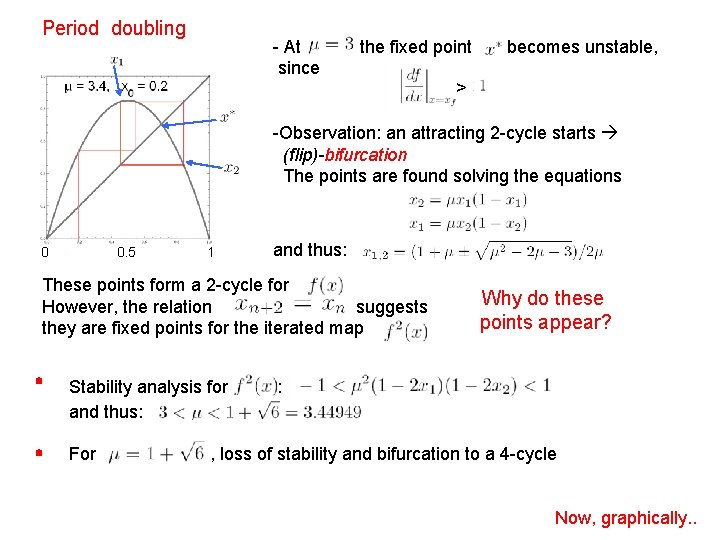
Period doubling - At since the fixed point becomes unstable, > -Observation: an attracting 2 -cycle starts (flip)-bifurcation The points are found solving the equations 0 0. 5 1 and thus: These points form a 2 -cycle for However, the relation suggests they are fixed points for the iterated map Stability analysis for and thus: For Why do these points appear? : , loss of stability and bifurcation to a 4 -cycle Now, graphically. .

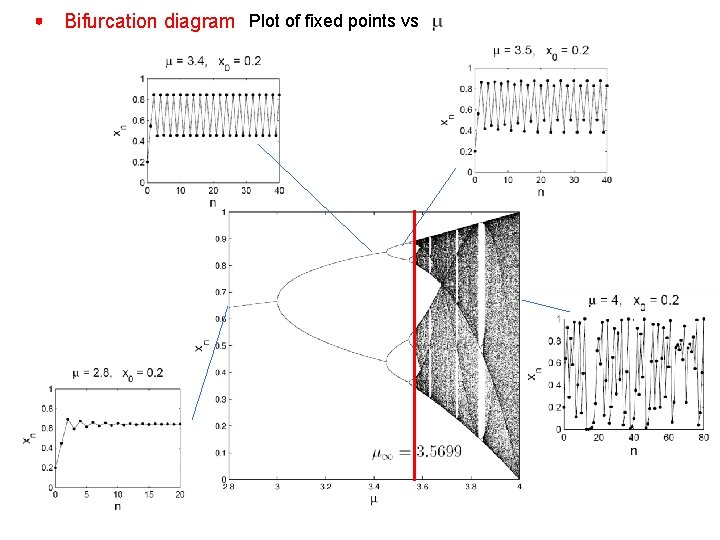
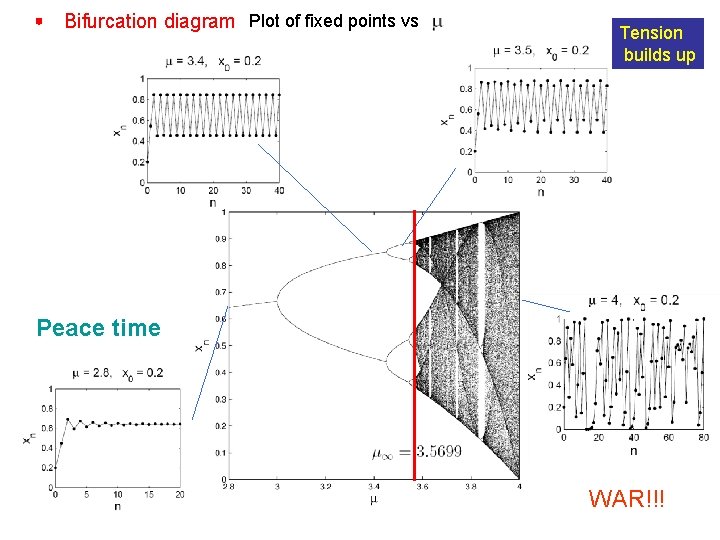
Bifurcation diagram Plot of fixed points vs

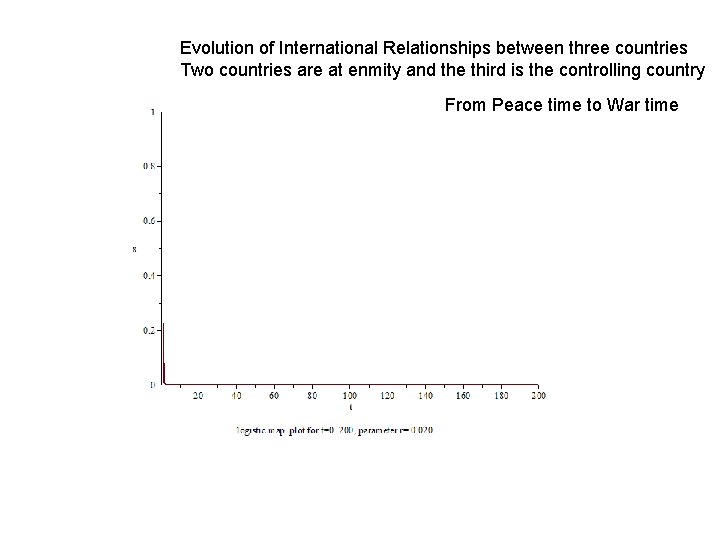
International Relations and Logistic Map Let A and B are two neighbouring countries Both countries look each other with enmity. Country A has x 1 fraction of the budget for the Defence for year 1 Country B has same fraction in its budget as soon as A’s budget session Is over Next year A has increased budget allocation x 2 Budget allocation goes on increasing. If complete budget is for Defence , it is not possible since no funds for Other areas

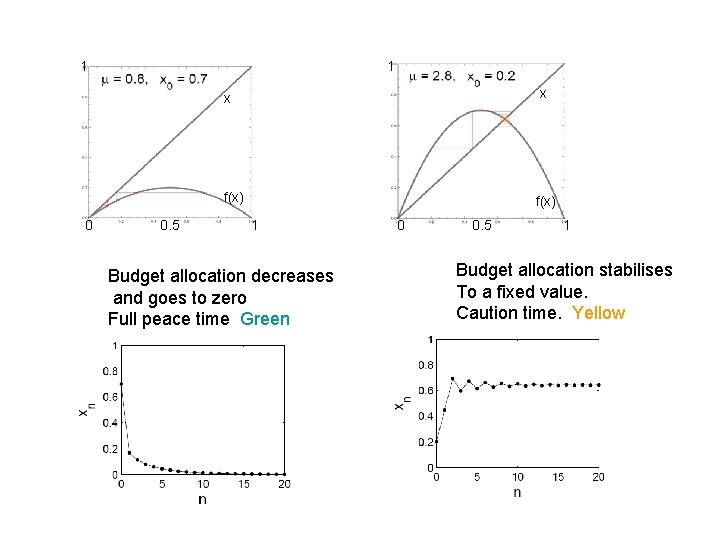
Fund allocation for subsequent years for the country A 1 x f(x) 0 0. 5 1 As time progresses, budget allocation for defense decreases. Peace time. A and B are friends.

Parameter μ is called enmity parameter. Now let a third country C intervenes In the region to modulate the enmity parameter and μ = μ(t)

Phenomenology of the logistic map a) b) 1 1 y=x fixed point c) f(x) 0 0. 5 2 -cycle? 0. 5 0 1 1 0 fixed point d) 1 What’s going on? 0. 5 1 1 chaos? 0 0. 5 1 Analyze first a) b) b) c) , …

1 1 x x f(x) 0 0. 5 f(x) 1 Budget allocation decreases and goes to zero Full peace time Green 0 0. 5 1 Budget allocation stabilises To a fixed value. Caution time. Yellow

Period doubling 1 Observations: x 1) The map oscillates between two values of x f(x) 0 0. 5 1 Evolution of the logistic map 2) Period doubling: What is it happening?

Bifurcation diagram Plot of fixed points vs Tension builds up Peace time WAR!!!

Evolution of International Relationships between three countries Two countries are at enmity and the third is the controlling country From Peace time to War time

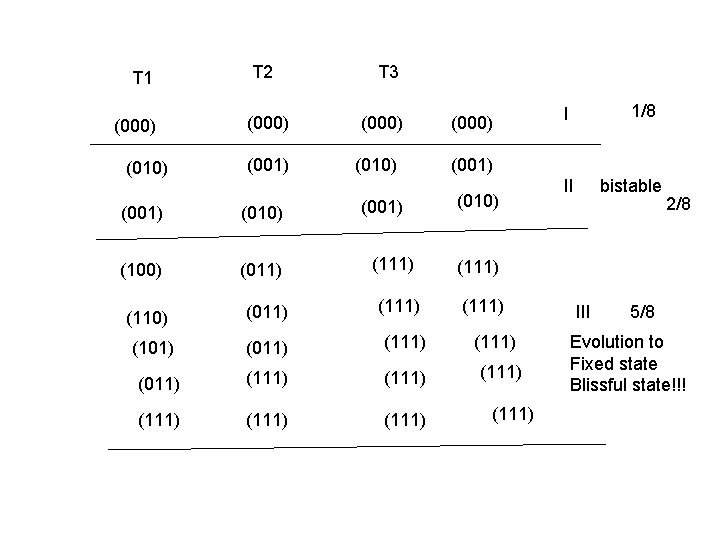
Interaction leads to modification of dynamics. A, B and C are three components of a system with two states YES (1) or NO ( 0) Case 1 A, B and C are non interacting Following are the 8 equal probable states of the system 1=( 000), 2=( 001), 3=(010), 4=( 100), 5=(110), 6=(101), 7=(011), 8=(111) Probability of occurrence is 1/8 for all the states. States evolve randomly. Case II Let A obeys AND logic gate while B and C obey OR logic gate

T 1 (000) (010) T 2 (000) (001) (010) (100) (011) (110) (011) T 3 (000) (010) (001) (111) (011) (111) (111) (101) (000) 1/8 I (001) (010) II bistable 2/8 (111) (111) III 5/8 Evolution to Fixed state Blissful state!!!

Bistable picture

Bistable picture

Rabbit and duck – bistable state

Photograph of melting ice landscape – Face of Jesus Christ - evolution leading to fixed state

Evolution – Esher’s painting

Nonlinearity in Optics

Linear Optics Maxwell’s Equations : Light -- Matter Interaction Maxwell’s equations for charge free, nonmagnetic medium . D = 0 . B = 0 XE = - B/ t XH = D/ t D = 0 E + P and B = 0 H In vacuum, P = 0 and on combining above eqns 2 E - 0 0 2 E/ t 2 = 0 or 2 E - 1/c 2 2 E/ t 2 = 0 In a medium, 2 E - 0 0 2 E/ t 2 - 0 2 P/ t 2 = 0 writing P = 0 E, 2 E - 1/v 2 2 E/ t 2 = 0 where, v = ( 0 )-1/2 Defining c/v = n, 2 E - n 2/c 2 2 E/ t 2 = 0 we get a second order linear diffl eqn describing what is called, Linear Optics

P= (1) E + (2) E 2 + (3)E 3 +…. . (n)/ (n+1) << 1 For isotropic medium, (n) will be scalar. (n) represents nth order non linear optical coefficient

Polarisation of a medium P = PL +PNL where, PL = (1) E and PNL = (2) E 2 + (3)E 3 +…. . On substituting P in the Maxwell’s eqns, we get 2 E - n 2/c 2 2 E/ t 2 = 0 2 PNL/ t 2 This is nonlinear differential equation and describes various types of Nonlinear optical phenomena. Type of NL effects exhibited by the medium depend the order of nonlinear optical coefficient. E Polarisation Maxwell’s eqns feedback

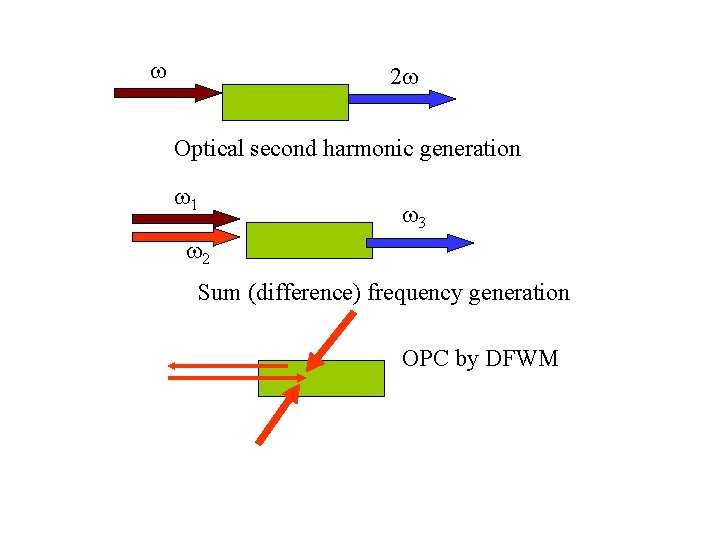
2 Optical second harmonic generation 1 3 2 Sum (difference) frequency generation OPC by DFWM

Consequence of 3 rd order optical nonlinearity intensity dependent complex refractive index

One of the consequences of 3 rd order NL PNL = (1)E + (3)E 3 =( (1) + (3)E 2)E = (n 1 + n 2 I)E We have n n(I) = (n 1 + n 2 I) n 2< 0 n 1 n 2> 0 I Intensity dependent ref. index has applications in self induced transparency, self focussing, optical limiting and in optical computing.

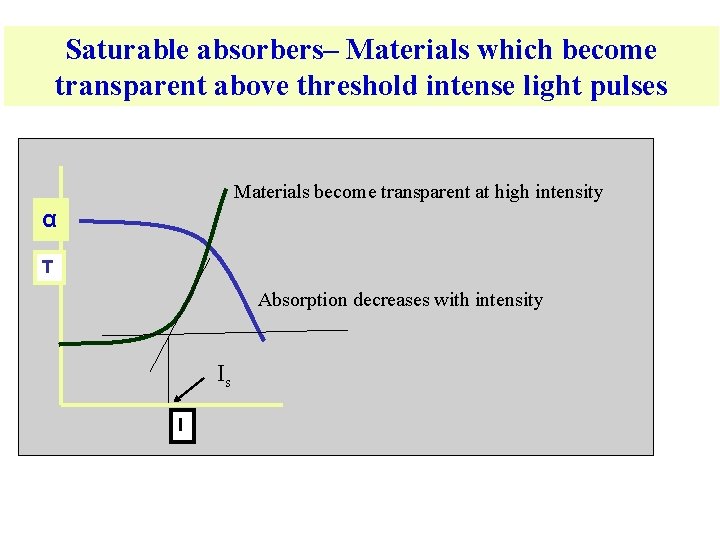
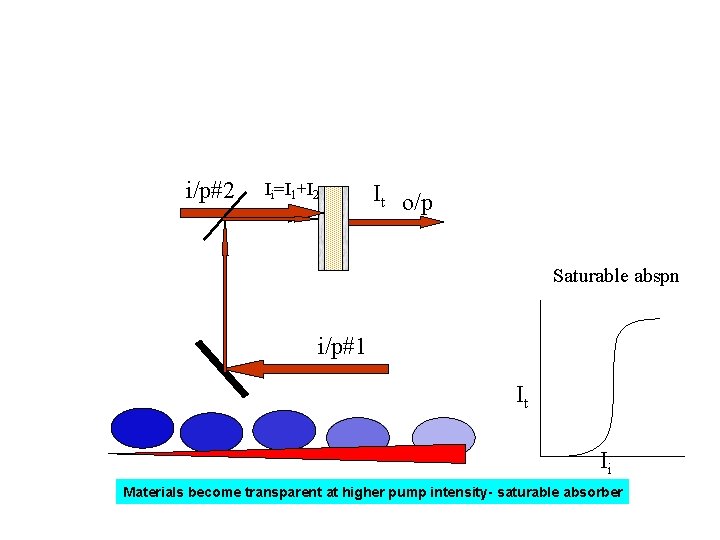
Saturable absorbers– Materials which become transparent above threshold intense light pulses Materials become transparent at high intensity α T Absorption decreases with intensity Is I

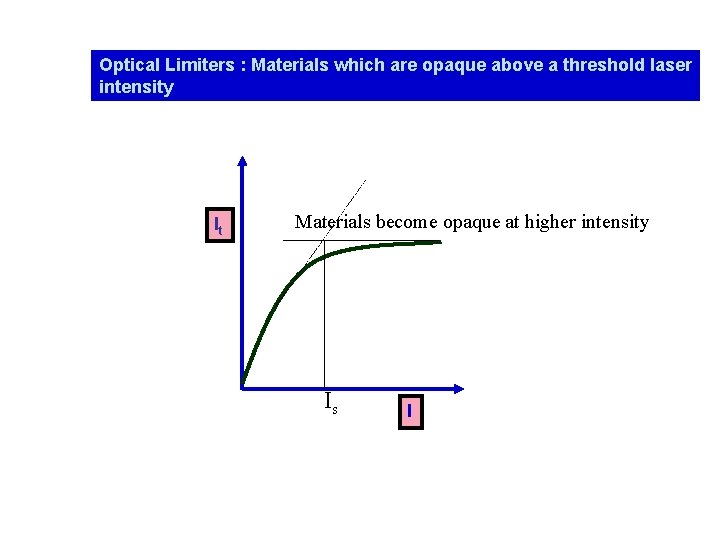
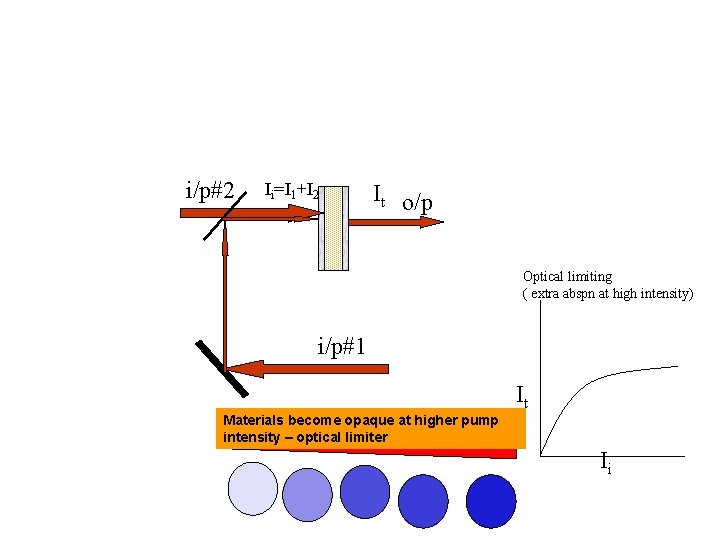
Optical Limiters : Materials which are opaque above a threshold laser intensity It Materials become opaque at higher intensity Is I

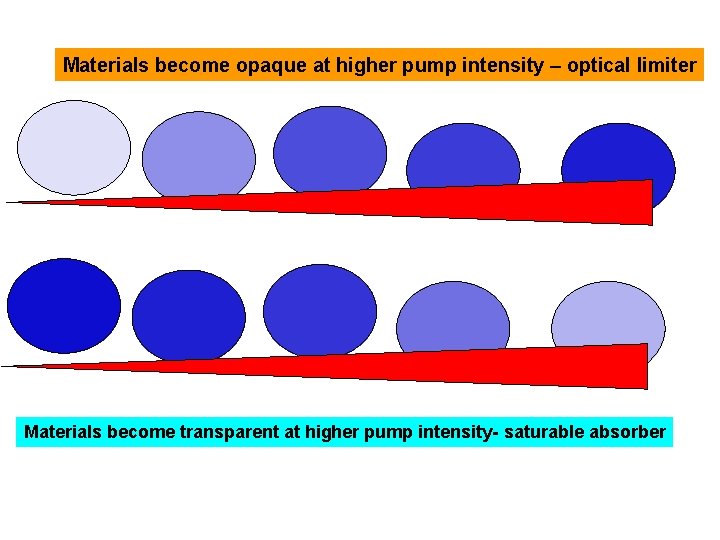
Materials become opaque at higher pump intensity – optical limiter Materials become transparent at higher pump intensity- saturable absorber

Optical limiters are used in…… v. Protection of eyes and sensitive devices from intense light pulses v. Laser mode locking v. Optical pulse shaping v. Optical signal processing and computing .

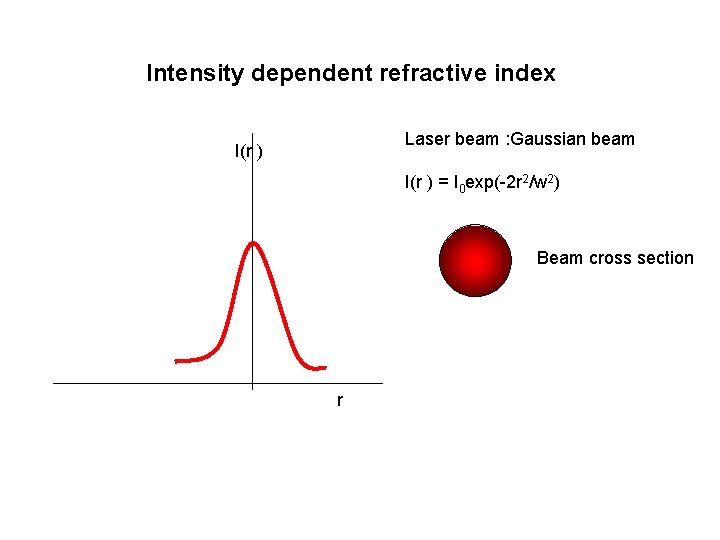
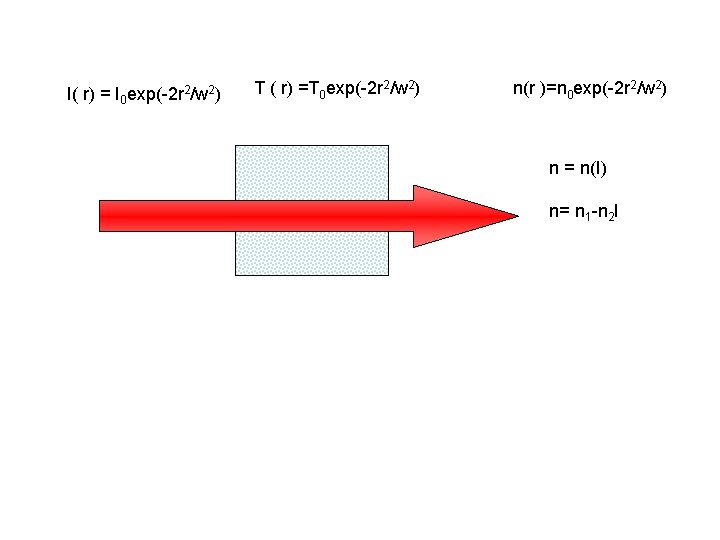
Intensity dependent refractive index Laser beam : Gaussian beam I(r ) = I 0 exp(-2 r 2/w 2) Beam cross section r

I( r) = I 0 exp(-2 r 2/w 2) T ( r) =T 0 exp(-2 r 2/w 2) n(r )=n 0 exp(-2 r 2/w 2) n = n(I) n= n 1 -n 2 I

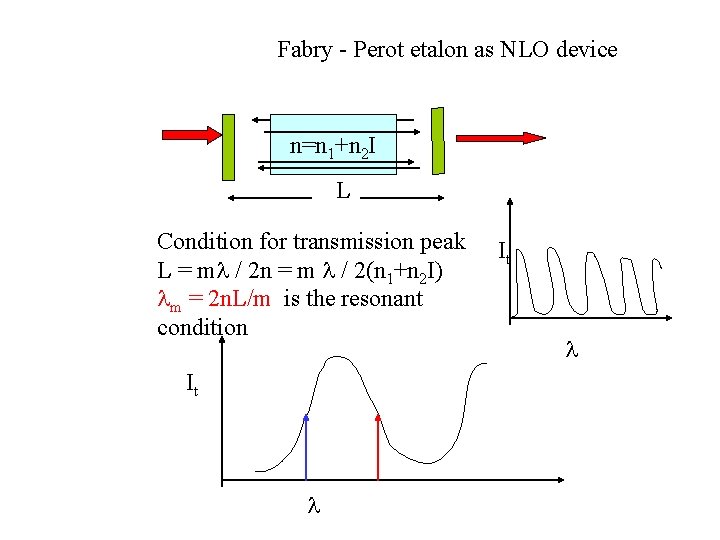
Fabry - Perot etalon as NLO device n=n 1+n 2 I L Condition for transmission peak L = m / 2 n = m / 2(n 1+n 2 I) m = 2 n. L/m is the resonant condition It It

i/p#2 Ii=I 1+I 2 It o/p Saturable abspn i/p#1 It Ii Materials become transparent at higher pump intensity- saturable absorber

i/p#2 Ii=I 1+I 2 It o/p Optical limiting ( extra abspn at high intensity) i/p#1 It Materials become opaque at higher pump intensity – optical limiter Ii

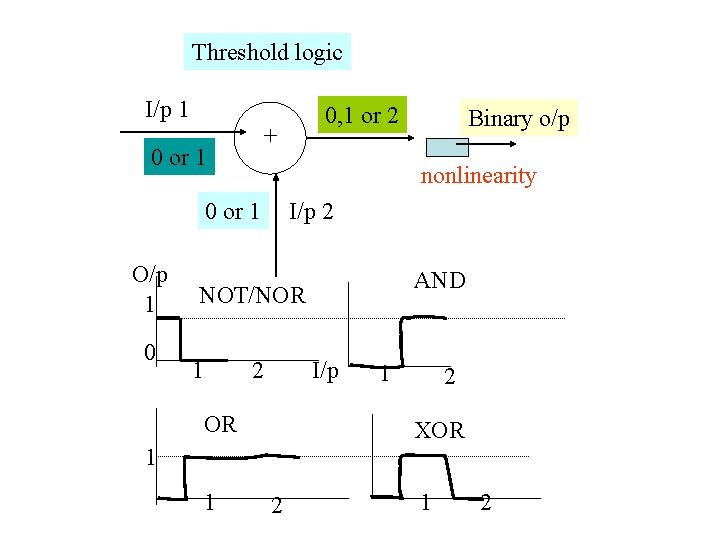
Threshold logic I/p 1 + 0 or 1 0 I/p 2 AND NOT/NOR 1 Binary o/p nonlinearity 0 or 1 O/p 1 0, 1 or 2 2 I/p OR 1 2 XOR 1 1 2

Z-scan Experiment Aperture Detector B Beam splitter Sample z A method to vary the intensity of pump beam incident on a sample: The sample is moved along a focused gaussian beam. Laser Intensity can be varied continuously with maximum at the focal point. Open aperture z-scan : Sensitive to nonlinear absorption of sample Closed aperture z-scan : Sensitive to both nonlinear absorption & refraction M S Bahae et. al; “High-sensitivity, single-beam n 2 measurements”, Opt Lett, 14, 955 (1989)

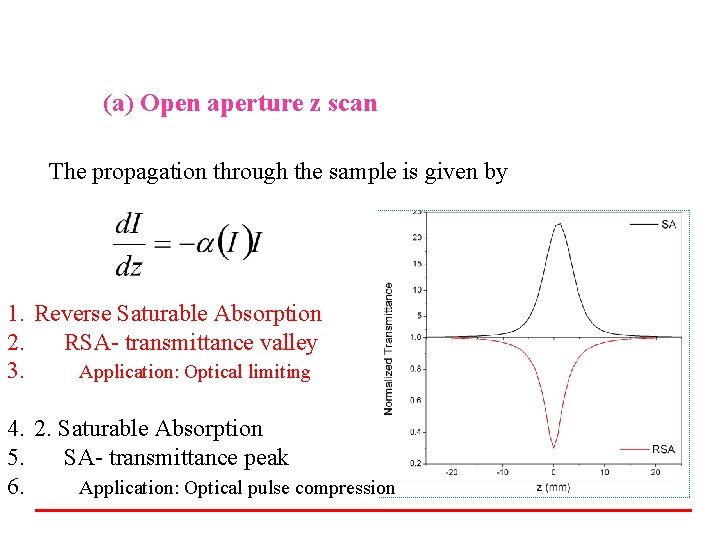
(a) Open aperture z scan The propagation through the sample is given by 1. Reverse Saturable Absorption 2. RSA- transmittance valley 3. Application: Optical limiting 4. 2. Saturable Absorption 5. SA- transmittance peak 6. Application: Optical pulse compression


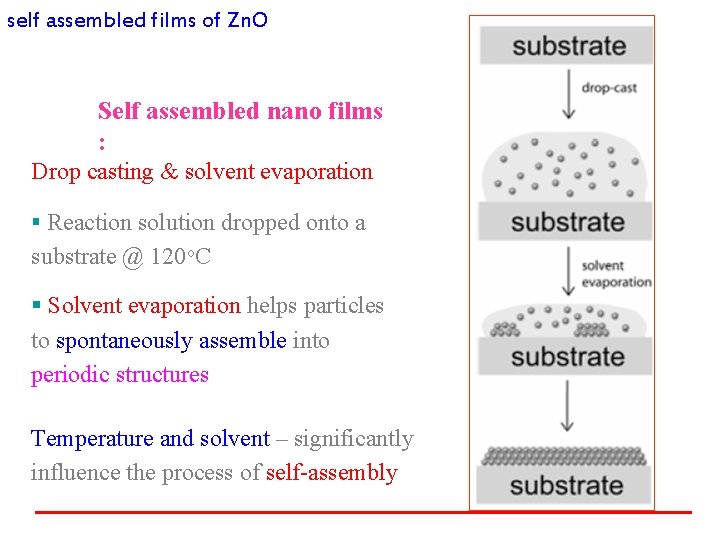
self assembled films of Zn. O Self assembled nano films : Drop casting & solvent evaporation § Reaction solution dropped onto a substrate @ 120 o. C § Solvent evaporation helps particles to spontaneously assemble into periodic structures Temperature and solvent – significantly influence the process of self-assembly

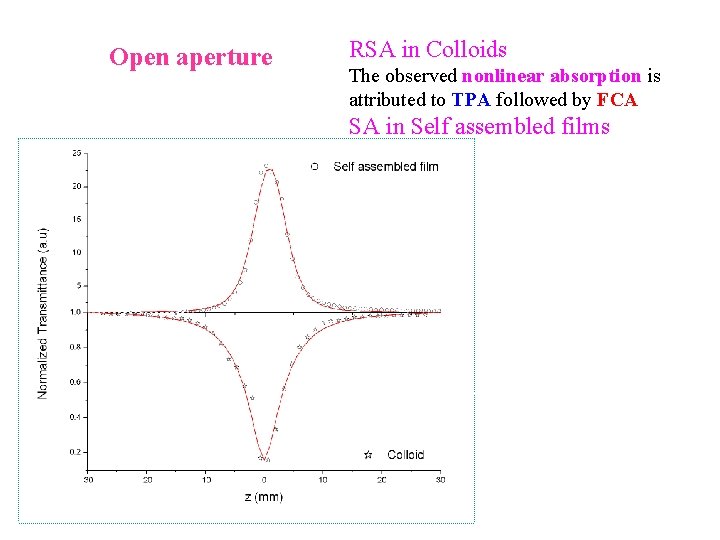
Open aperture RSA in Colloids The observed nonlinear absorption is attributed to TPA followed by FCA SA in Self assembled films

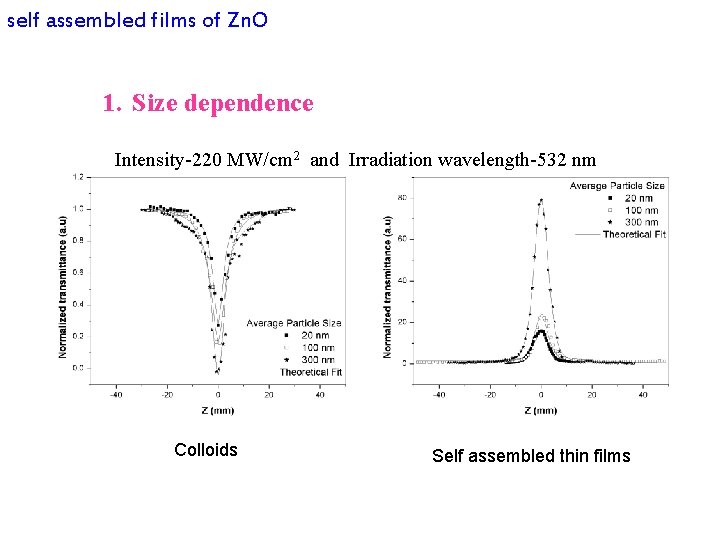
self assembled films of Zn. O 1. Size dependence Intensity-220 MW/cm 2 and Irradiation wavelength-532 nm Colloids Self assembled thin films

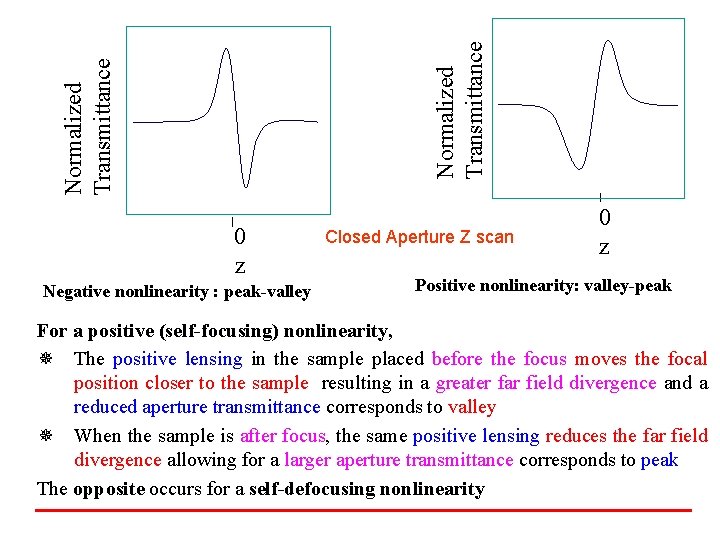
Normalized Transmittance 0 z Negative nonlinearity : peak-valley Closed Aperture Z scan 0 z Positive nonlinearity: valley-peak For a positive (self-focusing) nonlinearity, ¯ The positive lensing in the sample placed before the focus moves the focal position closer to the sample resulting in a greater far field divergence and a reduced aperture transmittance corresponds to valley ¯ When the sample is after focus, the same positive lensing reduces the far field divergence allowing for a larger aperture transmittance corresponds to peak The opposite occurs for a self-defocusing nonlinearity

To Conclude Nature is Nonlinear Linearity is an approximation for our convenience

 Isp cusat
Isp cusat Isp
Isp Trafford iapt
Trafford iapt Subnet isp telkom
Subnet isp telkom Isp master
Isp master Total isp solution
Total isp solution Saluran koneksi utama isp adalah
Saluran koneksi utama isp adalah Isp icp postfix
Isp icp postfix Mdu isp
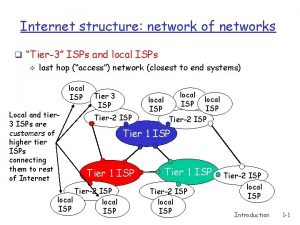
Mdu isp Tier 3 isp
Tier 3 isp Designing language curriculum
Designing language curriculum Tier 1 isp
Tier 1 isp Idaho state police forensics
Idaho state police forensics Isp
Isp Isp kuleuven
Isp kuleuven Wu isp
Wu isp Isp core
Isp core Trygar engineering
Trygar engineering Total isp solution
Total isp solution Isp varnost
Isp varnost Isp converged services
Isp converged services Intranet isp
Intranet isp Architecture of isp
Architecture of isp Isp help desk
Isp help desk Hhx tietgen studieretninger
Hhx tietgen studieretninger Person-centered isp example
Person-centered isp example Spitfire sip
Spitfire sip What are the advantages and disadvantages of email
What are the advantages and disadvantages of email Who isp
Who isp Elte ik telekommunikációs hálózatok
Elte ik telekommunikációs hálózatok Isp job description
Isp job description Total isp solution
Total isp solution Isp 080989999
Isp 080989999 Que es un isp en informatica
Que es un isp en informatica Eyeball isp
Eyeball isp Schematic table
Schematic table Mpls internet access
Mpls internet access X.toledo.ucll.be
X.toledo.ucll.be Gicona ispch
Gicona ispch Isp 080989999
Isp 080989999 Dr ahmer
Dr ahmer Isp defination
Isp defination Tier 1 isp
Tier 1 isp Isp icp postfix
Isp icp postfix Dbhds isp forms
Dbhds isp forms Makalah jaringan internet
Makalah jaringan internet Level 1 isp
Level 1 isp Isp islington
Isp islington Isp business model
Isp business model Isp help desk
Isp help desk Isp 250 uitm
Isp 250 uitm Wu isp
Wu isp Strindbergs fruar
Strindbergs fruar Fences character map
Fences character map August de prima porta
August de prima porta Diane august
Diane august Bunyi hukum hardy weinberg
Bunyi hukum hardy weinberg 2003 august 25
2003 august 25 August safety
August safety What happened on august 23 1939
What happened on august 23 1939 Agosto 30 1896 kaganapan
Agosto 30 1896 kaganapan August lec 250
August lec 250 Troy maxson analysis
Troy maxson analysis August hlond przepowiednie
August hlond przepowiednie August name pronunciation
August name pronunciation