I Recapof Discrete Computability CS 700 M Ziegler

I. Recapof Discrete. Computability CS 700 M. Ziegler § un-/computability, Halting Problem § Semi-/decidability, Reduction § Model of computation: WHILE prog. § SMN propery, Currying § "Oracle" computation, Limit Lemma, Arithmetic Hierarchy

Alan M. Turing 1941 1936 CS 700 M. Ziegler • first scientific calculations on digital computers • What are its fundamental limitations? decision + • Uncountably many P N A B' problem B x B' A • but countably many B' 'algorithms' • Undecidable Halting Problem H : No algorithm B can always correctly answer the following question simulator /interpreter B? Given A, x , does algorithm A terminate on input x? contradiction: B' that, Proof by contradiction : Consider • Logicians Tarski, Alonzo Churchalgorithm (Ph. D advisor) upon a positive on input A, executes on A, A and, • Kurt Gödel (1931): BThere exist arithmetical answer , loops infinitely. How B' behave on B' statements which are true butdoes cannot be proven so. ?

Un-/Semi-/Decidability I CS 700 M. Ziegler Definition: a) An 'algorithm' A computes a partial function f : N N = {0, 1, 2, …} if it • on inputs x dom(f) outputs f(x) and terminates, • on inputs x dom(f) does not terminate. Injective pairing function ("Hilbert Hotel") x, y : = x + (x+y)·(x+y+1)/2 b) A decides set L N if it computes its total char. function: cf. L(x): =1 for x L, cf. L(x): =0 for x L. c) A semi-decides L if terminates precisely on x L d) A enumerates L if it computes some total injective f: N N with L=range(f).

Un-/Semi-/Decidability II CS 700 M. Ziegler Example: The Halting problem H, considered as subset of N, is semi-decidable, not decidable. Theorem: a) Every finite L is decidable. b) L is decidable iff its complement L is. c) L is decidable iff both L, L are semi-decidable. d) L is enumerable iff infinite and semi-decidable. b) A decides set L N if it computes its total char. function: cf. L(x): =1 for x L, cf. L(x): =0 for x L. c) A semi-decides L if terminates precisely on x L d) A enumerates L if it computes some total injective f: N N with L=range(f).

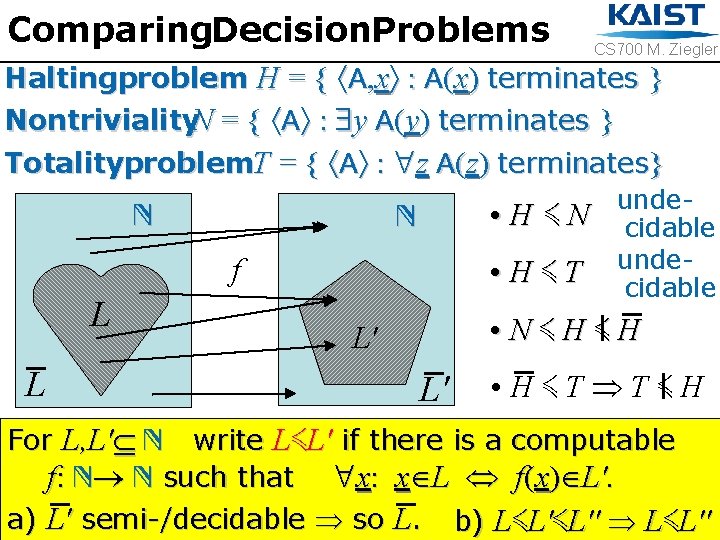
Comparing. Decision. Problems CS 700 M. Ziegler Haltingproblem H = { A, x : A(x) terminates } Nontriviality. N = { A : y A(y) terminates } Totalityproblem. T = { A : z A(z) terminates} N • H ≼N N f L L • H≼T undecidable • N≼H≼H L' L' • H≼T T≼H For L, L' N write L≼L' if there is a computable f: N N such that x: x L f(x) L'. a) L' semi-/decidable so L. b) L≼L'≼L'' L≼L''

WHILEPrograms CS 700 M. Ziegler Syntax in Backus—Naur Form: P : = ( xj : = 0 | xj : = 1 | xj : = xi + xk | xj : = xi 2 | P ; P | WHILE xj DO P END ) Semantics: loop executed as long as xj≠ 0 Definition: Let P N denote the encoding of WHILE program P (e. g. as ascii sequence). UTM-Theorem : There exists a WHILE program U that, given P N and x 1, …, xk N and N N, simulates P on input (x 1, …, xk) for N steps.

SMN Theorem: Currying CS 700 M. Ziegler Definition: Let C = P N denote the encoding of WHILE program P , P = C its inverse/decoding. Type conversion example f(x, y) = sin(x)·ey SMN-Theorem : There exists a WHILE program that, given P N and x N, returns P(x, · ) , where P(x, · )(y) : P(x, y) UTM-Theorm : There exists a WHILE program that, given P N, returns Q N with Q(x, y) = P(x) (y) and WHILE prg that, given P , Q , returns Q◦P

Oracle Computation CS 700 M. Ziegler P = ( xj : = 0 , 1 | xj : = xi xk | xj : = xi 2 | xj : = (xi) | P ; P | WHILE xj DO P END ) Fix some arbitrary total : N→N Write H as short for cf. H Lemma ("Shoenfield"): g: N→N is H H'-computable iff g(x)=limj f( x, j ) for some H-computable f: N→N. Def: b) P decides set L N if it computes its total char. function: cf. L(x): =1 for x L, cf. L(x): =0 for x L. c) P semi-decides L if terminates precisely on x L d) H = { P, x : P terminat. on input x } H': =HH

Proof (Sketch) Shoenfield CS 700 M. Ziegler P = ( xj : = 0 , 1 | xj : = xi xk | xj : = xi 2 | xj : = (xi) | P ; P | WHILE xj DO P END ) Let PH compute g. Fix x and initialize A={}=B. y=limj f( x, j ) J j≥J: f( x, j )=y. At each stage j=1, 2, . . . maintain: A H and purportedly B H={}. Lemma ("Shoenfield"): g: N→N is iff g(x)=limj f( x, j ) for some H-computable f: N→N. Simulate P on input x for j steps, answering all queries y A positive and y Q negative. Any query y neither in A nor in B tentatively add to B. If simulation of P terminates, stop the current stage j and restart for j+1. Simultaneously to simulating P, semi-decide "y H? " for all y B. . When y H, move y from B to A, abort current stage j and restart for j+1.

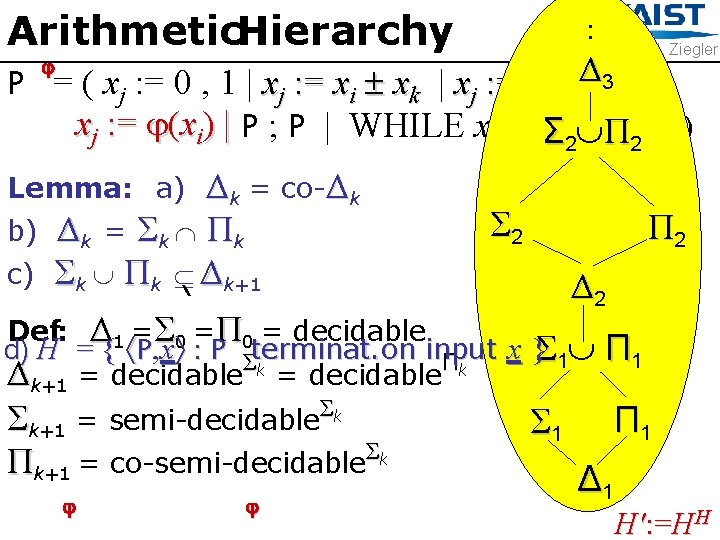
Arithmetic. Hierarchy : CS 700 M. Ziegler P = ( xj : = 0 , 1 | xj : = xi xk | xj : = xi Δ 23| xj : = (xi) | P ; P | WHILE xj DOΣ 2 P END Π 2 ) Δk = co-Δk Δ k = Σk Π k Σk Πk Δk+1 Lemma: a) b) c) Σ 2 Π 2 Δ 2 Def: Δ 1 =Σ 0 =Π 0 = decidable d) H = { P, x : P Σterminat. on input x }Σ 1 Π Δk+1 = decidable k Σk Σk+1 = semi-decidable Σk Πk+1 = co-semi-decidable Σ 1 Π 1 Δ 1 H': =HH

I. Recapof Discrete. Computability CS 700 M. Ziegler § un-/computability, Halting Problem § Semi-/decidability, Reduction § Model of computation: WHILE prog. § SMN propery, Currying § "Oracle" computation, Limit Lemma, Arithmetic Hierarchy