i Min Max B C Ooi K L

i. Min. Max B. C. Ooi, K. -L Tan, C. Yu, S. Stephen. Indexing the Edges -- A Simple and Yet Efficient Approach to High dimensional Indexing. ACM SIGMOD-SIGACTSIGART 19 th Symposium on Principles of Database Systems (PODS), 166 -174, (2000).

Query Requirement • Window/Range query: Retrieve data points fall within a given range along each dimension. • Designed to support range retrieval, facilitate joins and similarity search (if applicable).

Strategies • Increase Fan-Out by increasing the node size, as in X-trees. --- reduce indexing to semi-sequential scan? • Increase Fan-Out by using approximation in the nodes, as in A-trees – expensive update. • Mapping high-dimensional points into single-dimensional points by using space-filling curves methods. – Transformation is expensive. – The number of sub-queries generated can be very big. • Sequential scan needs to search the whole data file -affected volume is 100%.

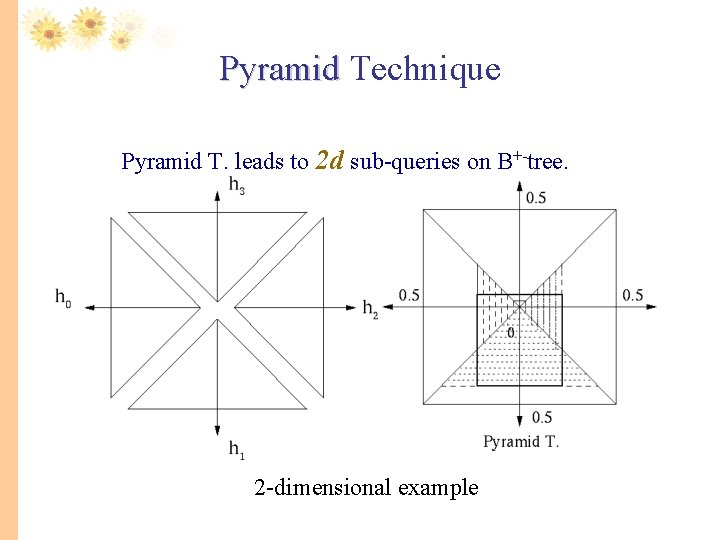
Pyramid Technique Pyramid T. leads to 2 d sub-queries on B+-tree. 2 -dimensional example

VA-file (Vector Approximation file) • Map objects to approximate bit strings. Eg. (0. 1 , 0. 8) ( 00, 11) • Basic Idea: divide data space to 2 b cells, each with a representation (bit string). • Scan whole signature file sequentially • Weakness: lost precision of data and hence affect the size of query window Eg. (0. 2, 0. 8) (0. 0, 1. 0) (00, 11) , which is as same as

i. Min. Max -- Basic Concept • ‘Edge’ --- the max/min attribute of data point, which is also closer to the data space edge, comparing with other attributes. B (0. 6, 0. 9) Consider unit data space ([0, 1], [0, 1] … [0, 1]) e. g. point A (0. 1, 0. 6), edge = 0. 1; point B (0. 6, 0. 9), edge = 0. 9; A (0. 1, 0. 6) • A data point whose “edge” not included in a query range is not an answer.

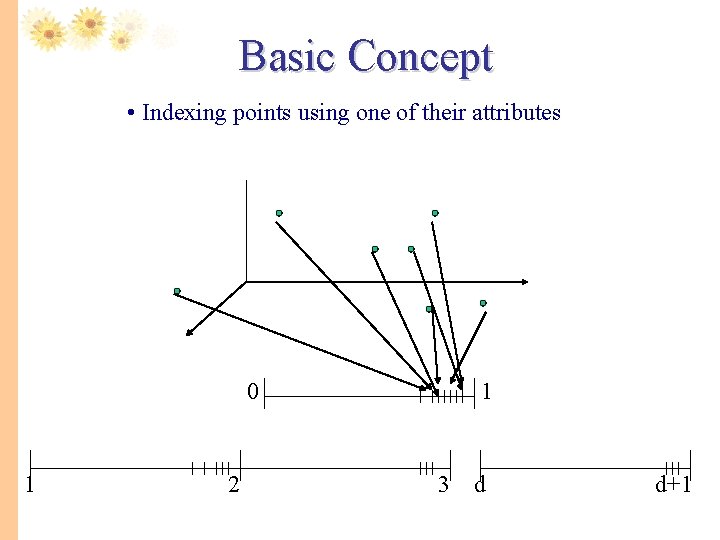
Basic Concept • Indexing points using one of their attributes 0 1 2 1 3 d d+1

Basic Concept • The probability of finding an attribute with very large (small) value increases with dimensionality. Eg. In 2 -dim space [0. . 1], P(xi > 0. 9) = 0. 19 In 30 -dim space, P(xi > 0. 9) = 0. 958 (Uniform distribution) • However, not all queries will search for large values. ---- Use this fact to “prune” away data points that are of no interest !

i. Max or i. Min • Using the max. /min. attribute to build the index • Only at most d sub-queries needed • Algorithm is very simple. data point: range query: e. g. i. Max key . sub-query is * Similar arguments apply for i. Min. y>x x>y x

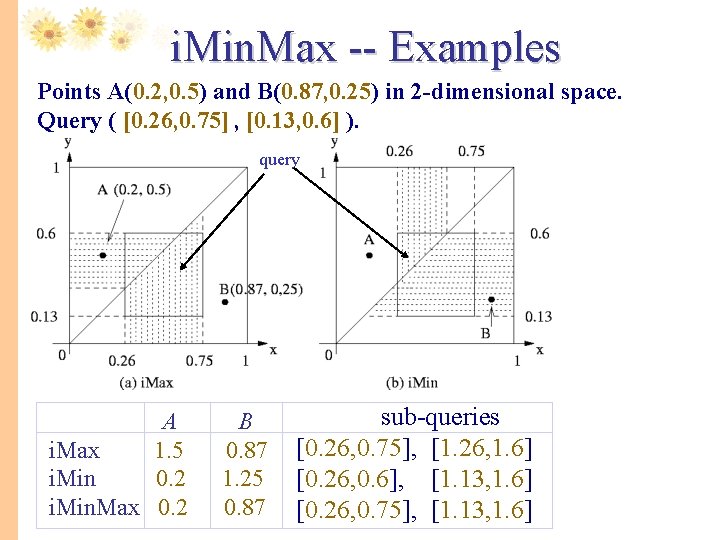
i. Min. Max -- Examples Points A(0. 2, 0. 5) and B(0. 87, 0. 25) in 2 -dimensional space. Query ( [0. 26, 0. 75] , [0. 13, 0. 6] ). query A i. Max 1. 5 i. Min 0. 2 i. Min. Max 0. 2 B 0. 87 1. 25 0. 87 sub-queries [0. 26, 0. 75], [1. 26, 1. 6] [0. 26, 0. 6], [1. 13, 1. 6] [0. 26, 0. 75], [1. 13, 1. 6]

i. Min. Max’s Principle • Algorithm of i. Min. Max is still very simple. ---- i. Min. Max key: sub-query: For d-dimensional space, at most d sub-queries are needed. The union of of all answers of subqueries yields the total answer. •

Operations • Range search: a query is transformed into d sub-queries, and for each, a normal B+-tree range search is performed. • Point search: an attribute is selected based i. Min. Max criteria, and an exact match search is performed. • Update: similar to those of B+-trees. B+-tree

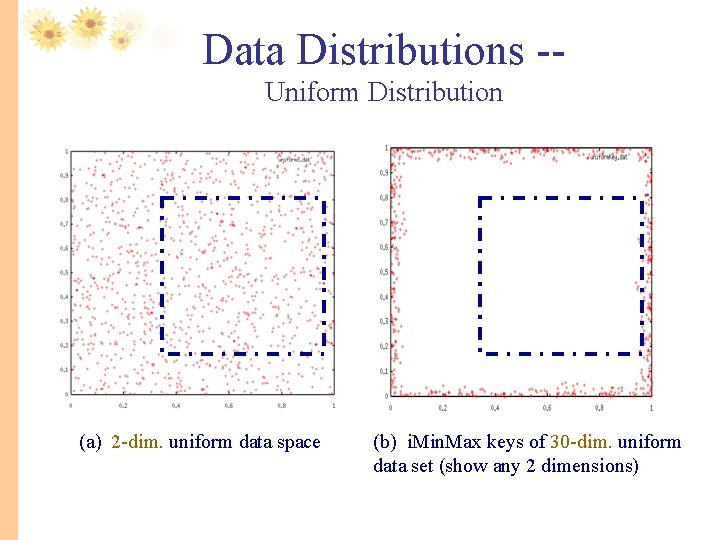
Data Distributions -Uniform Distribution (a) 2 -dim. uniform data space (b) i. Min. Max keys of 30 -dim. uniform data set (show any 2 dimensions)

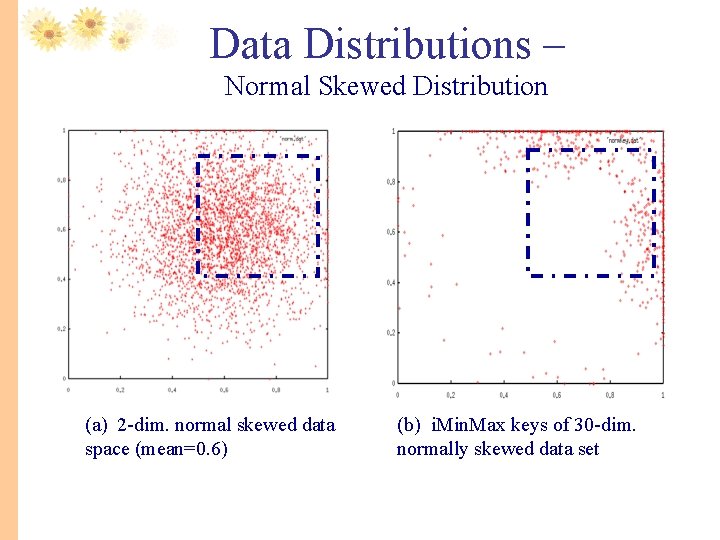
Data Distributions – Normal Skewed Distribution (a) 2 -dim. normal skewed data space (mean=0. 6) (b) i. Min. Max keys of 30 -dim. normally skewed data set

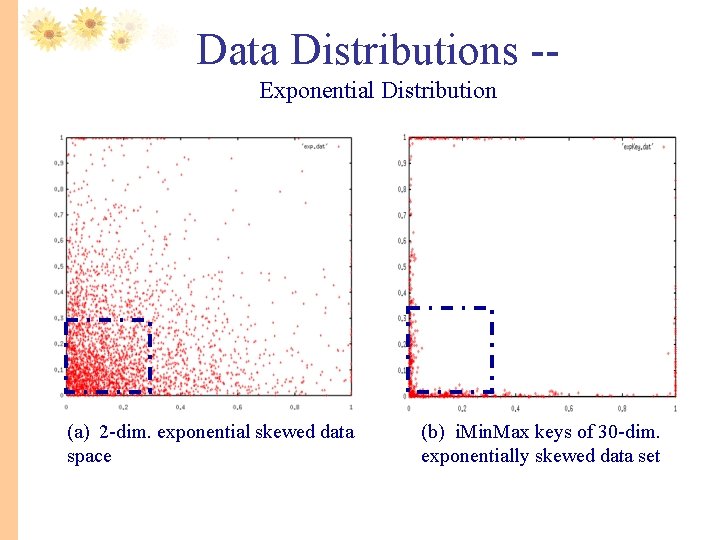
Data Distributions -Exponential Distribution (a) 2 -dim. exponential skewed data space (b) i. Min. Max keys of 30 -dim. exponentially skewed data set

i. Min. Max( i. Min. Max )’s Principle • Introduce to tune i. Min. Max for better performance. i. Min. Max( ) key: sub-query is still: ( independent of ) E. g. Set = 0. 2, Point (0. 1, 0. 8), Query ([0, 0. 6], [0. 1, 0. 7]) key i. Min. Max 0. 1 i. Min. Max( ) 1. 8 sub-queries [0, 0. 6] , [1. 1, 1. 7] checked not checked

Performance Study • Default data distribution: uniform on [0. . 1] • Default data set: 500 K • Default query selectivity: 0. 1%

Performance Study -i. Min. Max( i. Min. Max ) on skewed data Data size Dimension Query side Normal distribution 100 K, 500 K 30 0. 4 -0. 3 ~ 0. 3 (0. 5) Exponential distribution 500 K 30 0. 4 -0. 1 ~ 0. 4 * The distribution of query range is the same as the data set. * Data sets skewed with different degree, the tuning effects are different. * The tuning ‘knob’, , enables i. Min. Max to scatter the skewed data points to reduce false drops.

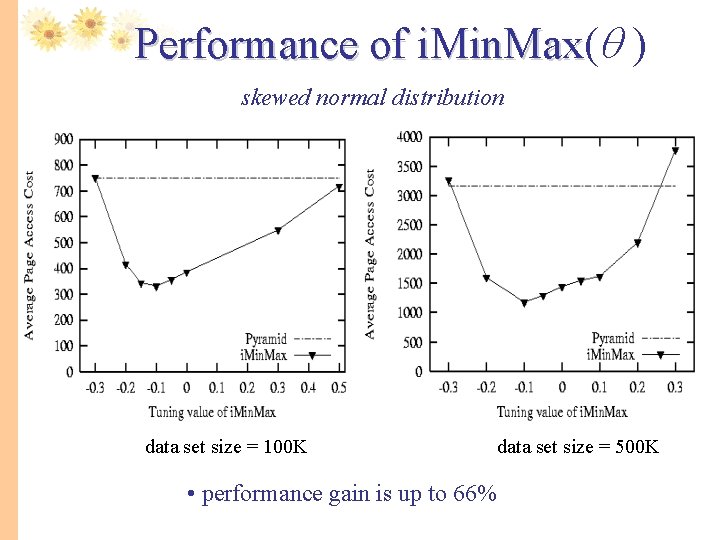
Performance of i. Min. Max( i. Min. Max ) skewed normal distribution data set size = 100 K • performance gain is up to 66% data set size = 500 K

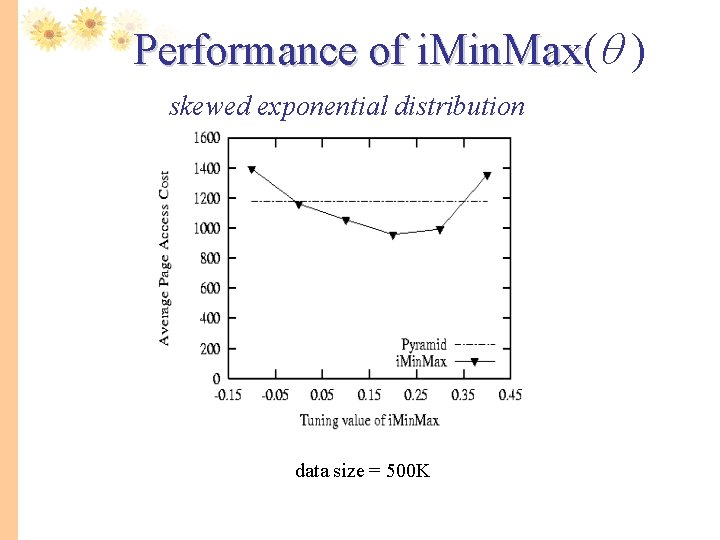
Performance of i. Min. Max( i. Min. Max ) skewed exponential distribution data size = 500 K