I A 4 r e t p a

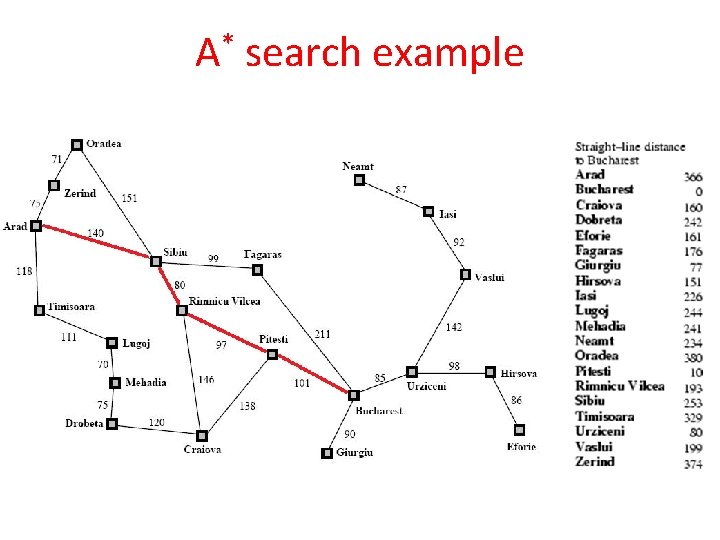
I A 4 r e t p a h C Informed search algorithms

Outline • • • Best-first search Greedy best-first search A* search Heuristics Local search algorithms Hill-climbing search Simulated annealing search Local beam search Genetic algorithms

Best-first search An informed search strategy uses problem-specific knowledge beyond the definition of the problem itself, so it can find solutions more efficiently than an uninformed strategy. Best-first search is an instance of the general TREE-SEARCH or GRAPH-SEARCH algorithm in which a node is selected for expansion based on an evaluation function, f (n). • A key component of these algorithms is a heuristic function denoted h(n) : h(n) = estimated cost of the cheapest path from node n to a goal node, if n is a goal node, then h(n) = 0.

Best-first search Special cases: • Greedy best-first search • A* search

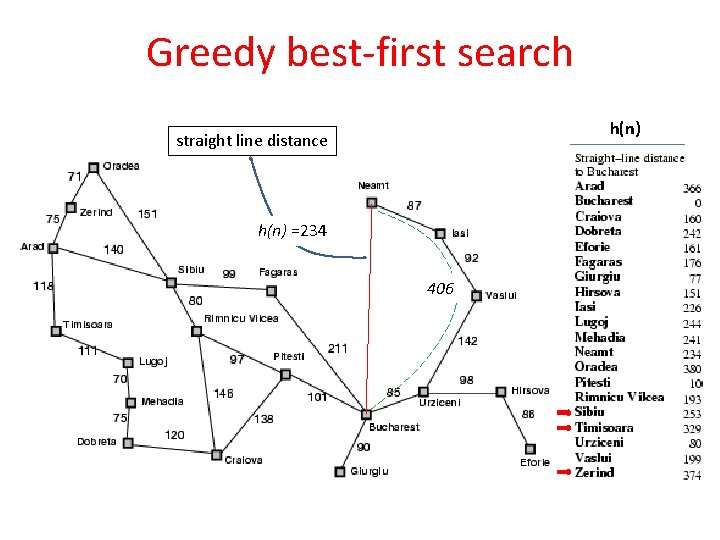
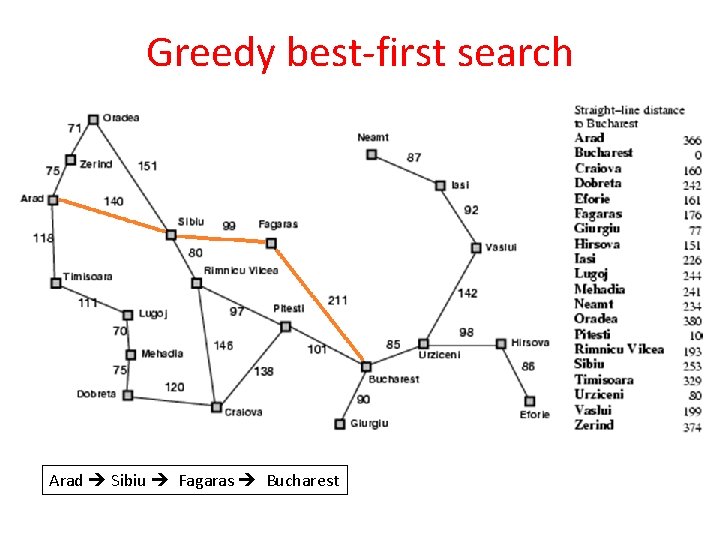
Greedy best-first search q. Greedy best-first search tries to expand the node that is closest to the goal, on the grounds that it is likely to lead to a solution quickly. q. Thus, it evaluates nodes by using just the heuristic function; that is, f(n)=h(n). q. Evaluation function f(n) = h(n) (heuristic) = estimate of cost from n to goal q. Assume h. SLD(n) = straight line distance from n to Bucharest, so Greedy best-first search expands the node that appears to be closest to goal

Greedy best-first search h(n) straight line distance h(n) =234 406

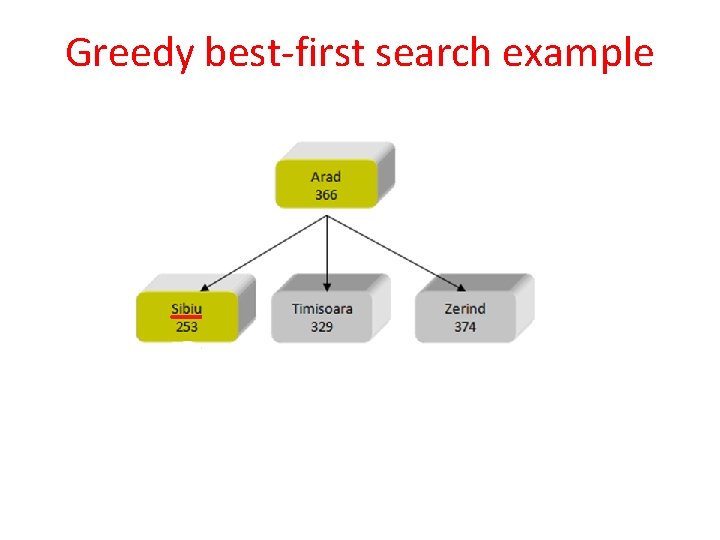
Greedy best-first search example

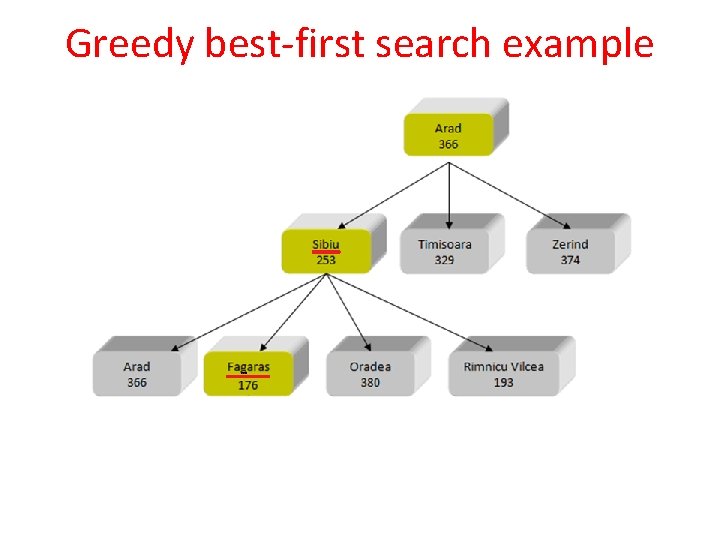
Greedy best-first search example

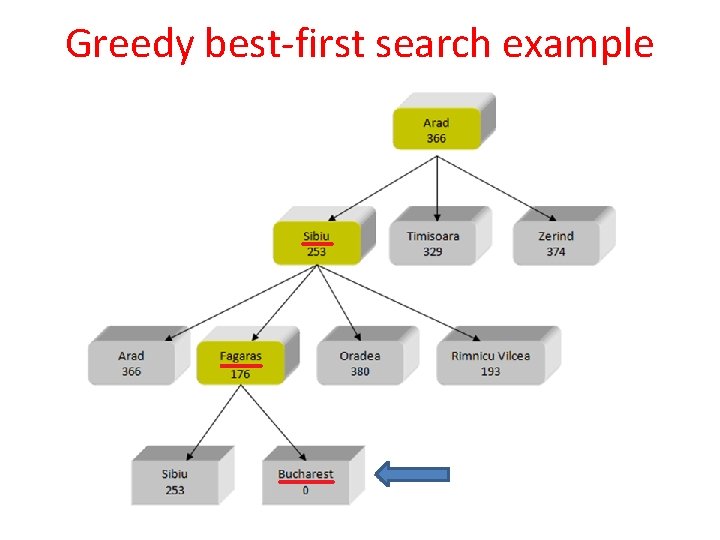
Greedy best-first search example

Greedy best-first search example

Greedy best-first search Arad Sibiu Fagaras Bucharest

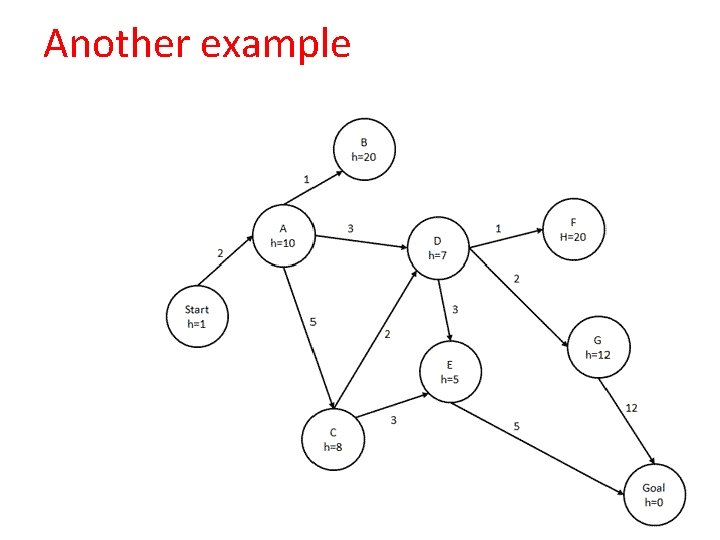
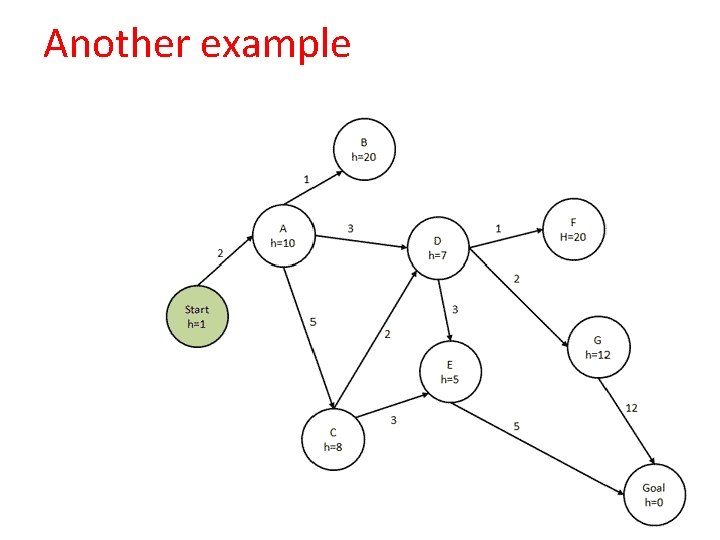
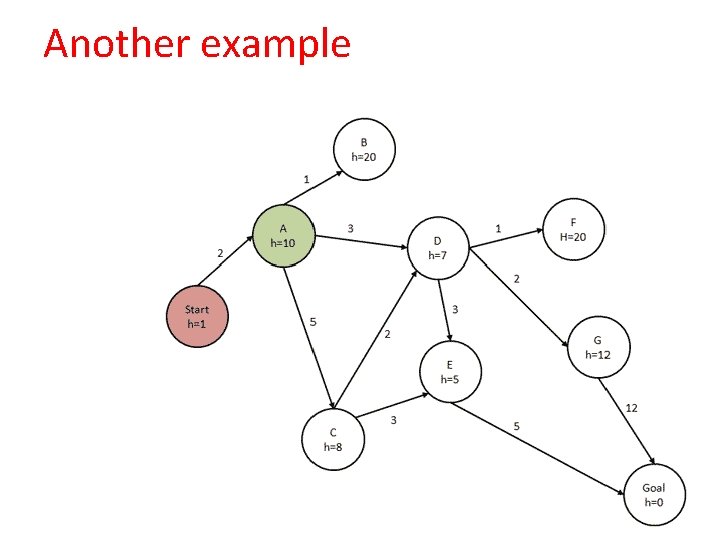
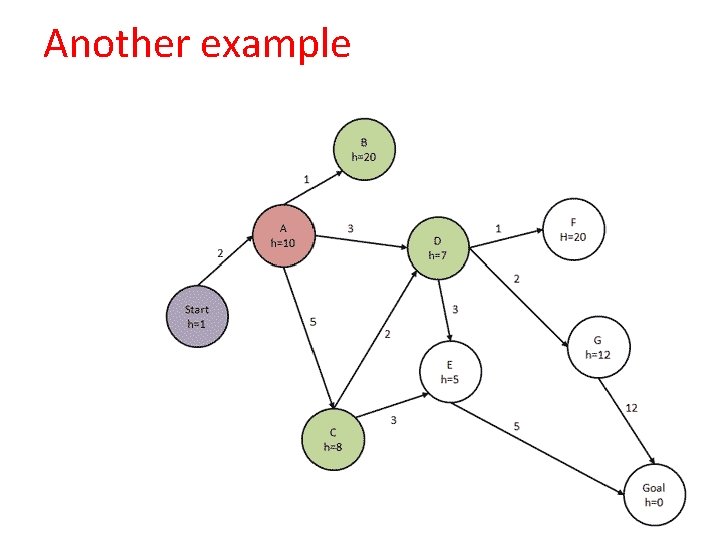
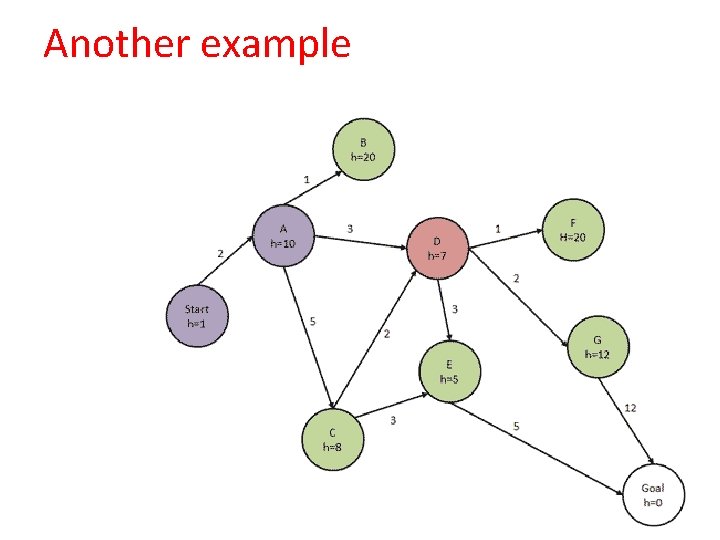
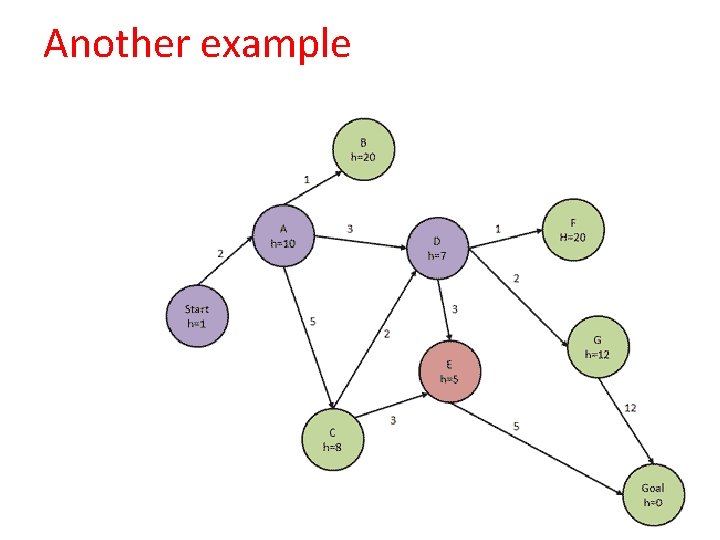
Another example

Another example

Another example

Another example

Another example

Another example

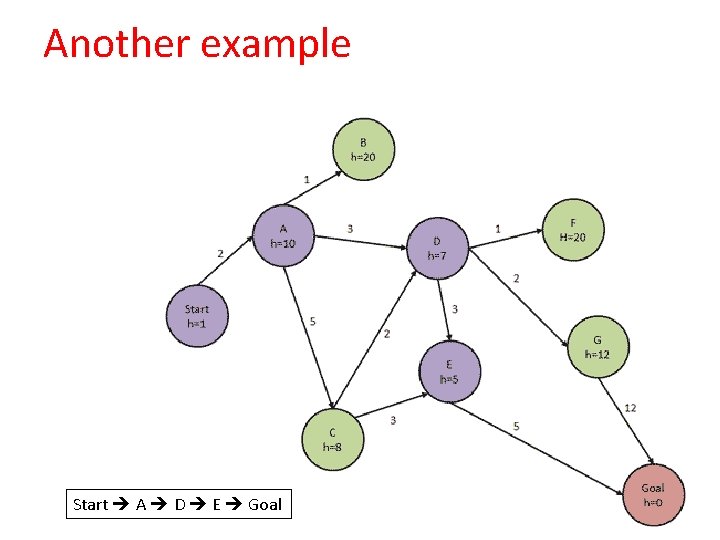
Another example Start A D E Goal

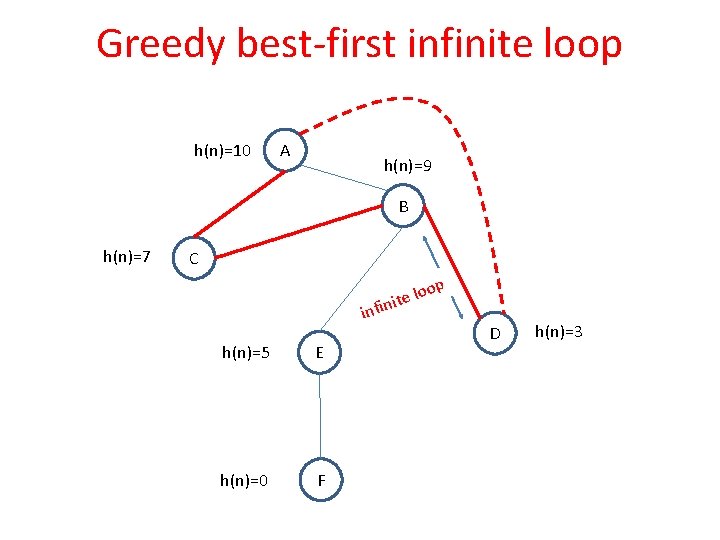
Greedy best-first infinite loop h(n)=10 A h(n)=9 B h(n)=7 C op o l e finit in h(n)=5 E h(n)=0 F D h(n)=3

Greedy best-first not optimal h(n)=10 A h(n)=9 h(n)=7 h(n)=5 C h(n)=4 D E h(n)=2 G h(n)=3 F H h(n)=0 B

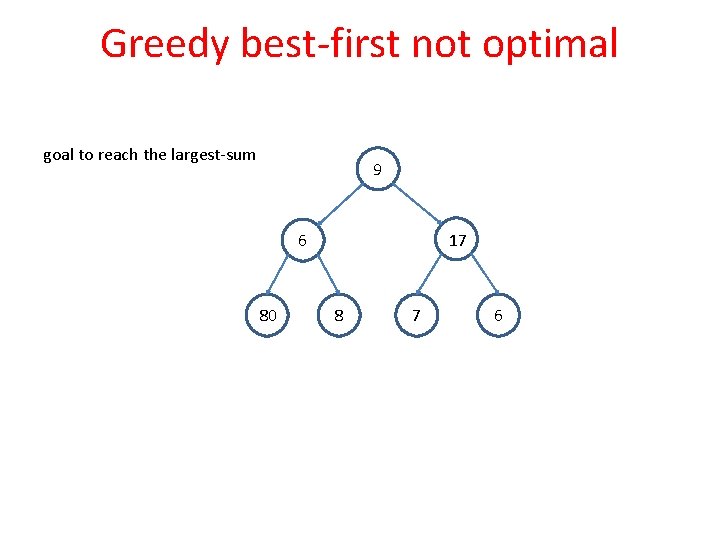
Greedy best-first not optimal goal to reach the largest-sum 9 17 6 80 8 7 6

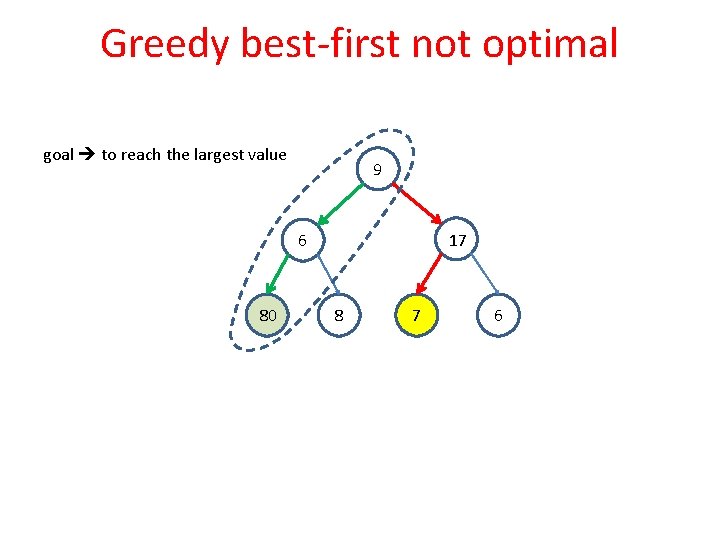
Greedy best-first not optimal goal to reach the largest value 9 17 6 80 8 7 6

Greedy best-first not optimal goal to reach the largest value 9 17 6 80 8 7 6

Properties of greedy best-first search • Complete? No – can get stuck in loops • Time? O(bm), but a good heuristic can give dramatic improvement • Space? O(bm), keeps all nodes in memory • Optimal? No, may even produce the unique worst possible solution b = branching factor m = max depth of search tree

A* search Minimizing the total estimated solution cost q The most widely known form of best-first search is called A* search (pronounced "A-star search"). q It evaluates nodes by combining g(n), the cost to reach the node, and h(n), the cost to get from the node to the goal: Evaluation function f(n) = g(n) + h(n) Where g(n) gives the path cost from the start node to node n, and h(n) is the estimated cost of the cheapest path from n to the goal f (n) = estimated cost of the cheapest solution through n

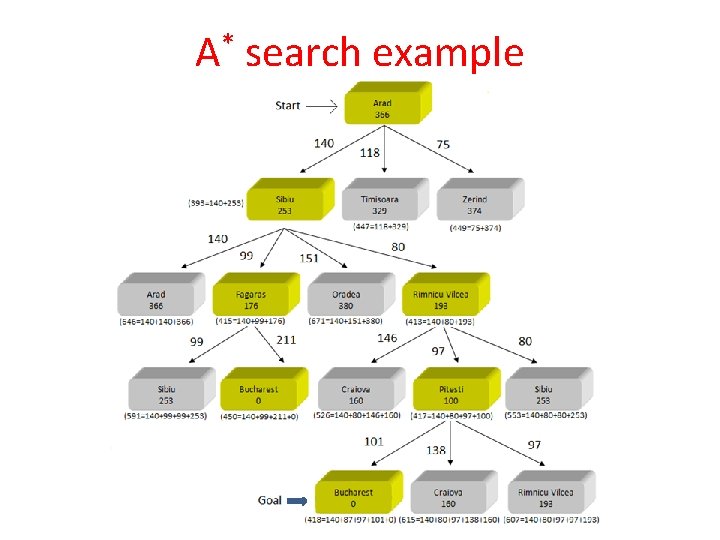
A* search example

A* search example

A* search example tracing

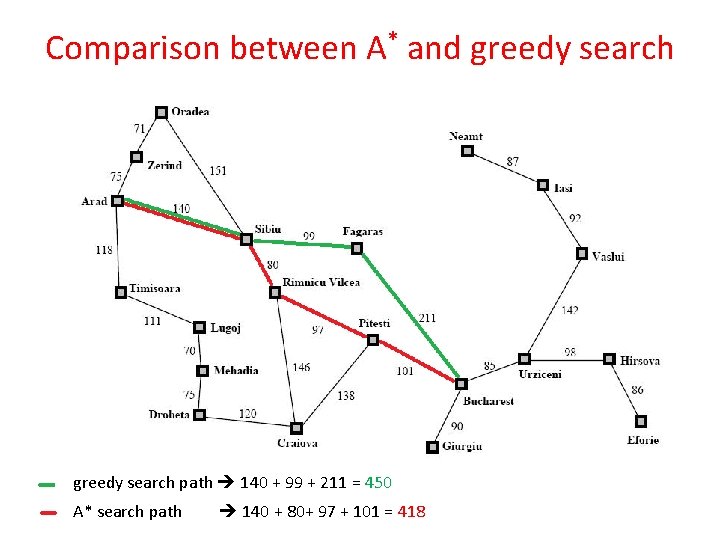
Comparison between A* and greedy search path 140 + 99 + 211 = 450 A* search path 140 + 80+ 97 + 101 = 418

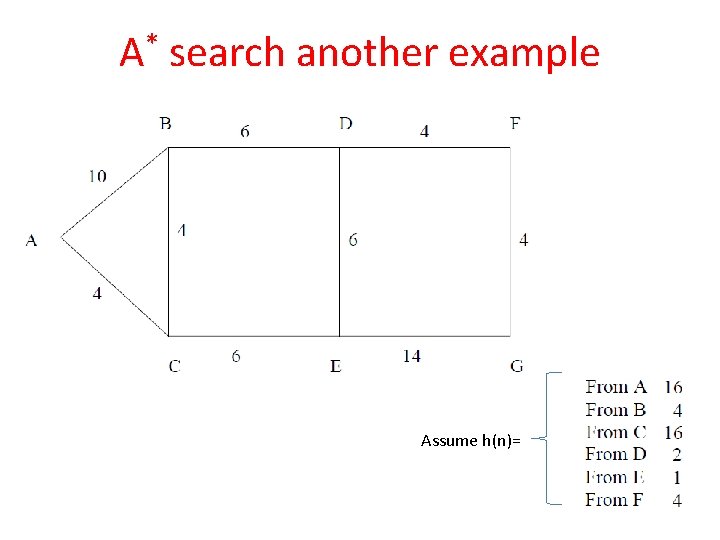
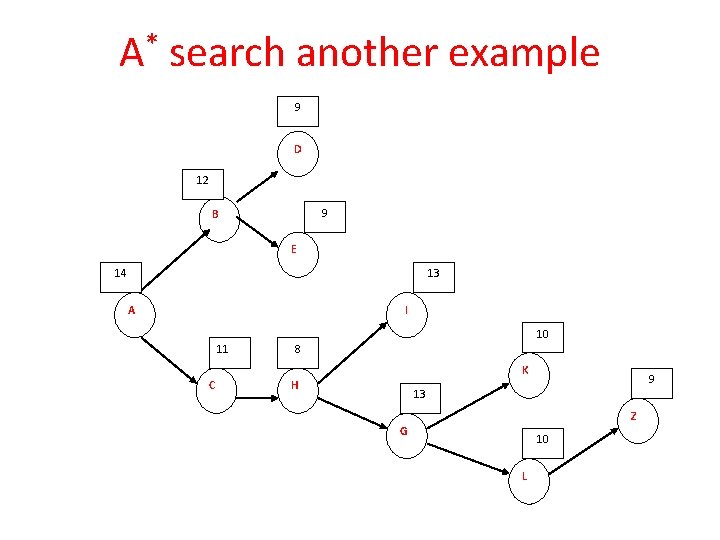
A* search another example Assume h(n)=

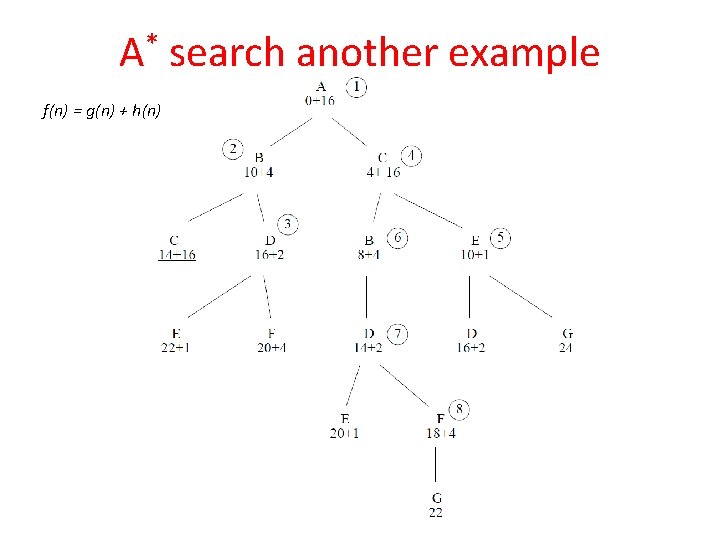
A* search another example f(n) = g(n) + h(n)

A* search another example 9 D 12 9 B E 14 13 A I 10 11 8 K C H 9 13 Z G 10 L

Properties of A* • • Complete? Yes Time? Exponential (time is not main drawback) Space? Keeps all nodes in memory Optimal? Yes

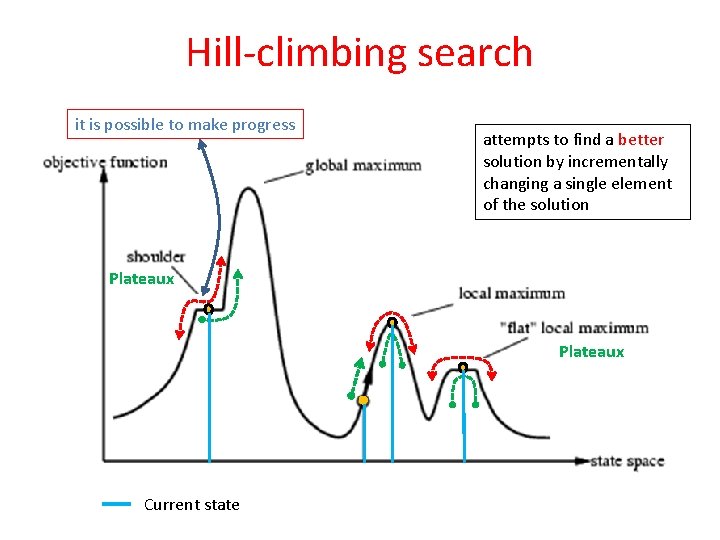
Hill-climbing search "Like climbing Everest in thick fog with amnesia" It is simply a loop that continually moves in the direction of increasing value-that is, uphill. It terminates when it reaches a "peak" where no neighbor has a higher value. The basic idea is to proceed according to some heuristic measurement of the remaining distance to the goal. depending on initial state, can get stuck in local maxima

Hill-climbing search it is possible to make progress attempts to find a better solution by incrementally changing a single element of the solution Plateaux Current state

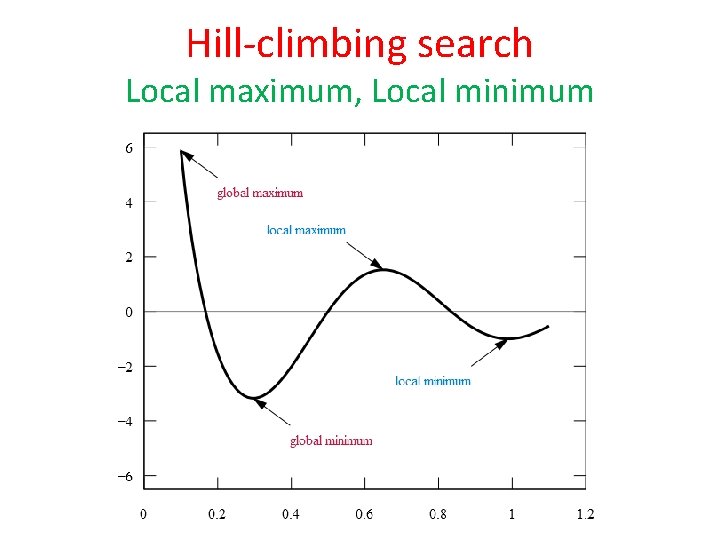
Hill-climbing search Local maxima: a local maximum is a peak that is higher than each of its neighboring states, but lower than the global maximum. Hill-climbing algorithms that reach the vicinity of a local maximum will be drawn upwards towards the peak, but will then be stuck with nowhere else to go. Plateaux: a plateau is an area of the state space landscape where the evaluation function is flat. It can be a flat local maximum, from which no uphill exit exists, or a shoulder, from which it is possible to make progress. Ridges: Ridges result in a sequence of local maxima that is very difficult for greedy algorithms to navigate. (the search direction is not towards the top but towards the side)

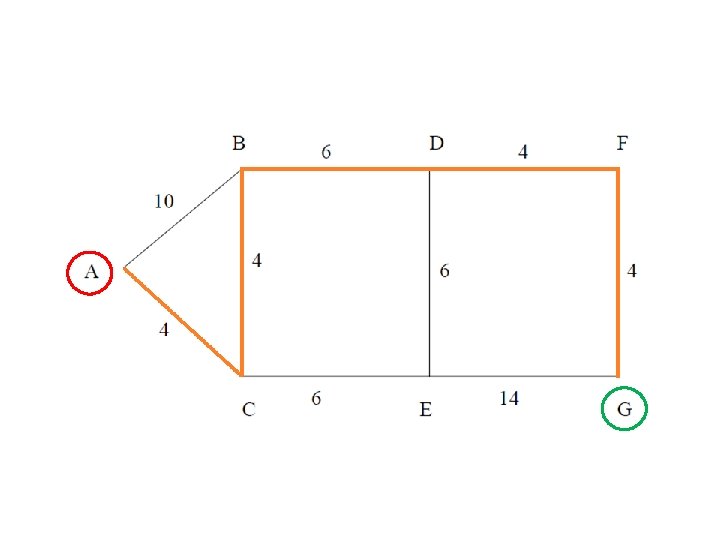
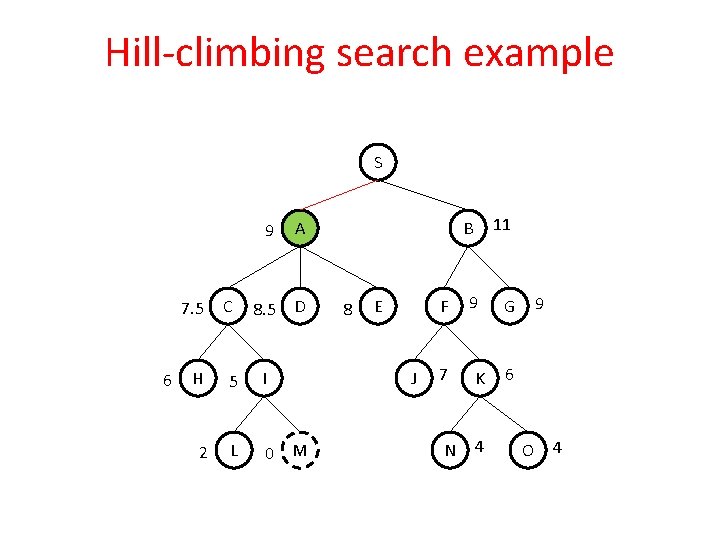
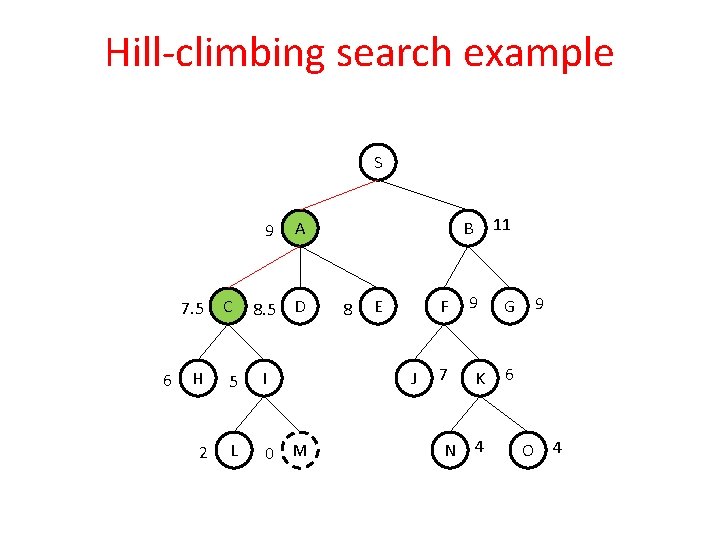
Hill-climbing search example our aim is to find a path from S to M associate heuristics with every node, that is the straight line distance from the path terminating city to the goal city S 7. 5 6 C 9 A 8. 5 D H 5 I 2 L 0 M 11 B 8 E F J 9 7 K N 4 9 G 6 O 4

Hill-climbing search example S 7. 5 6 C 9 A 8. 5 D H 5 I 2 L 0 M 11 B 8 E F J 9 7 K N 4 9 G 6 O 4

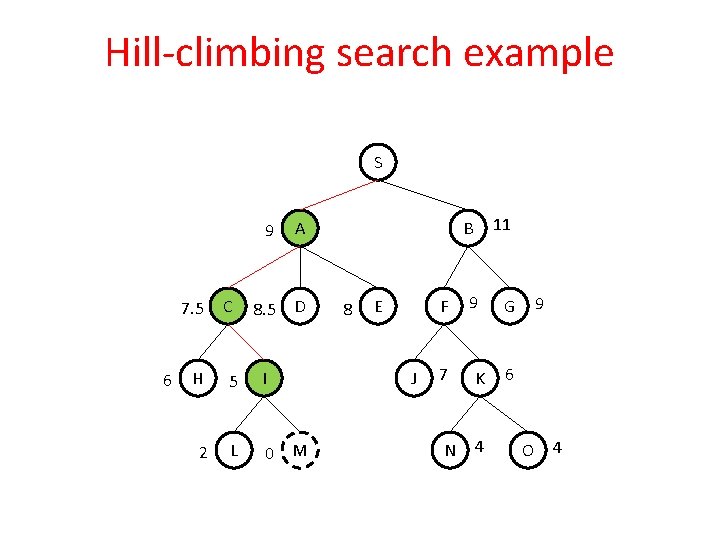
Hill-climbing search example S 7. 5 6 C 9 A 8. 5 D H 5 I 2 L 0 M 11 B 8 E F J 9 7 K N 4 9 G 6 O 4

Hill-climbing search example S 7. 5 6 C 9 A 8. 5 D H 5 I 2 L 0 M 11 B 8 E F J 9 7 K N 4 9 G 6 O 4

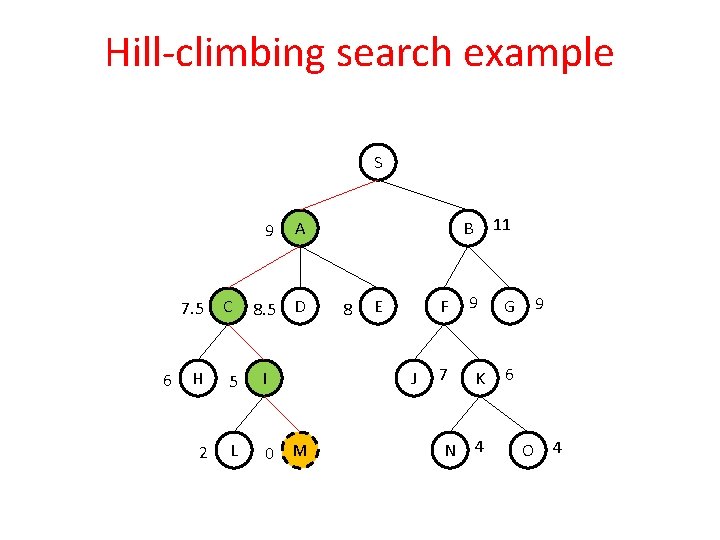
Hill-climbing search example S 7. 5 6 C 9 A 8. 5 D H 5 I 2 L 0 M 11 B 8 E F J 9 7 K N 4 9 G 6 O 4

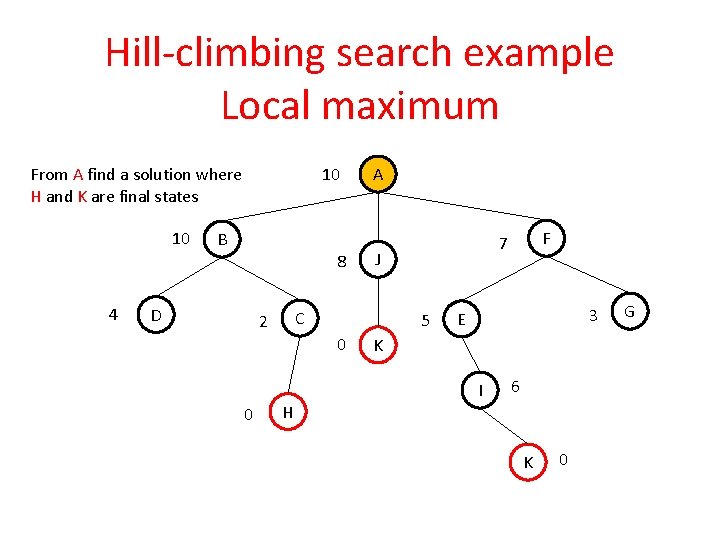
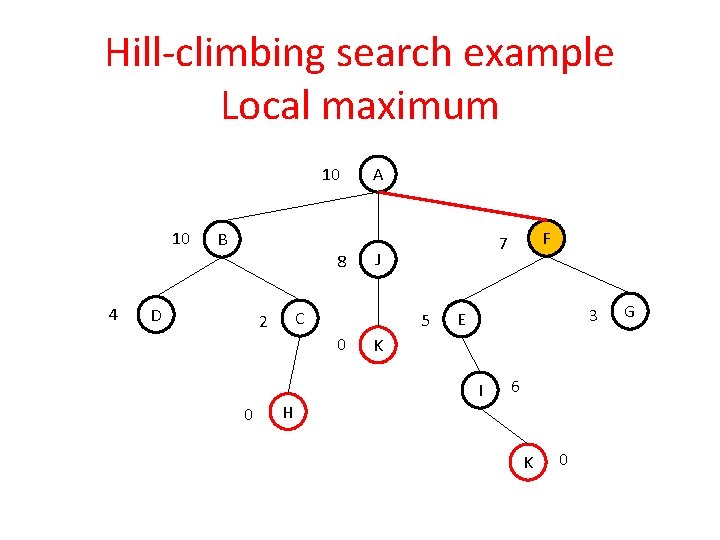
Hill-climbing search example Local maximum From A find a solution where H and K are final states 10 10 B 8 4 D 5 0 H F 7 J C 2 0 A 3 E K I 6 K 0 G

Hill-climbing search example Local maximum 10 10 B 8 4 D 5 0 H F 7 J C 2 0 A 3 E K I 6 K 0 G

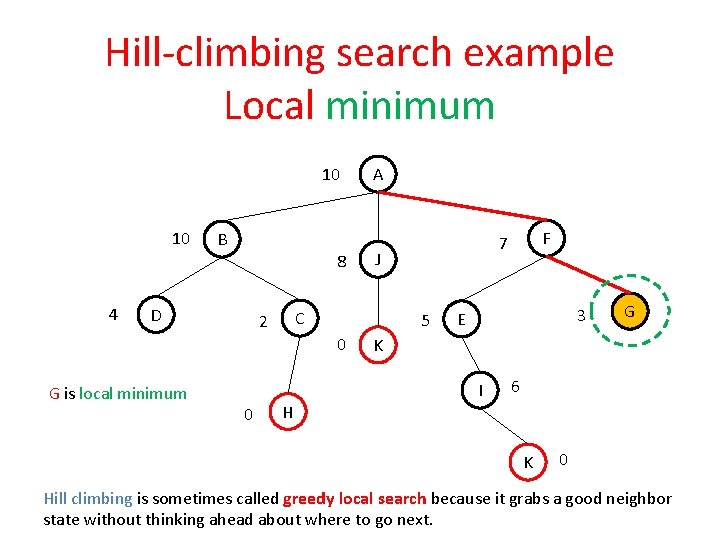
Hill-climbing search example Local minimum 10 10 B 8 4 D 0 H F 7 J C 2 5 0 G is local minimum A 3 E G K I 6 K 0 Hill climbing is sometimes called greedy local search because it grabs a good neighbor state without thinking ahead about where to go next.

Hill-climbing search Local maximum, Local minimum

END