i 206 Lecture 3 Boolean Logic Logic Circuits

i 206: Lecture 3: Boolean Logic, Logic Circuits Marti Hearst Spring 2012 1

Today • Quick Binary Exercise • Boolean Logic – de. Morgan’s Law • How Bits are Made • Relating Boolean Logic to Circuits – Logic gates 2

Review Binary • Binary used as a code • Can use binary to encode a game representation. Shapes Colors Actions 3

Review Binary Shape: 3 (2 bits) Color: 5 (3 bits) Action: 2 (1 bit) • Two approaches: modular and efficient • Modular: – Shape bits, then color bits, then action bits • 00 111 1 (circle, blue, jump) – Allows for expansion if you allow extra bits – Make it work for 7 colors: • 00 1000 1 • Efficient: – Minimize the number of bits needed – There a total of 5 * 3 * 2 = 30 unique states • So minimum number of bits = 5� – 6 bits can �support 7 * 3 * 2 = 42, for 7 colors, but would not be modular representation. 4

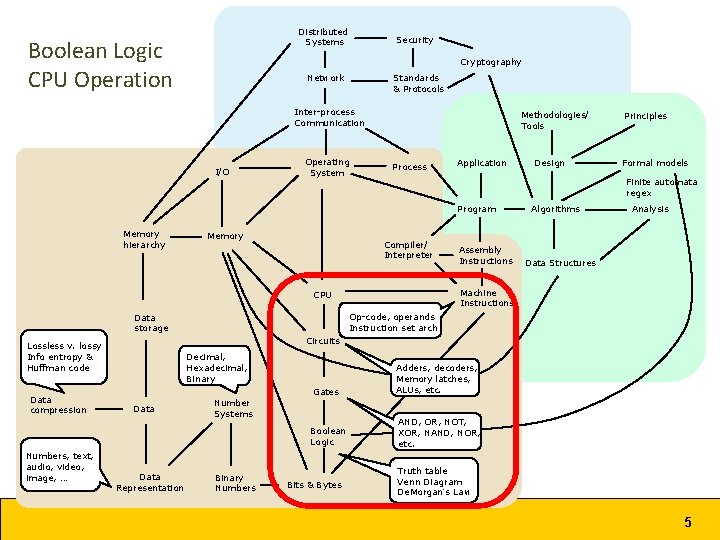
Distributed Systems Boolean Logic CPU Operation Security Cryptography Network Standards & Protocols Inter-process Communication I/O Operating System Methodologies/ Tools Process Application Memory Compiler/ Interpreter Analysis Data Structures Op-code, operands Instruction set arch Data storage Circuits Lossless v. lossy Info entropy & Huffman code Numbers, text, audio, video, image, … Assembly Instructions Algorithms Machine Instructions CPU Data compression Formal models Finite automata regex Program Memory hierarchy Design Principles Decimal, Hexadecimal, Binary Data Representation Gates Adders, decoders, Memory latches, ALUs, etc. Boolean Logic AND, OR, NOT, XOR, NAND, NOR, etc. Number Systems Binary Numbers Bits & Bytes Truth table Venn Diagram De. Morgan’s Law 5

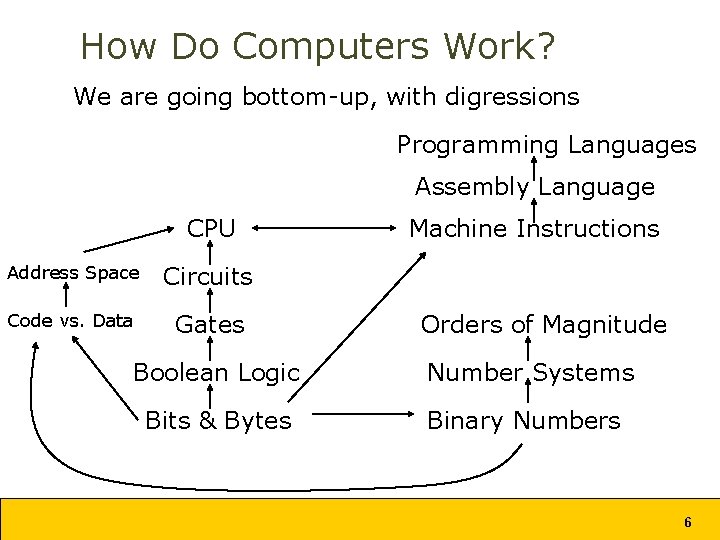
How Do Computers Work? We are going bottom-up, with digressions Programming Languages Assembly Language CPU Address Space Circuits Code vs. Data Gates Machine Instructions Orders of Magnitude Boolean Logic Number Systems Bits & Bytes Binary Numbers 6

Boolean Logic • Boolean algebra = logical calculation of truth values (true/false values) • Basic boolean operators – – AND OR XOR (exclusive-OR) NOT 7

Boolean Logic • Where else have we seen this? • Queries! – (“apple” OR “pear” OR “berry”) AND (“juice” OR “smoothie”) • Venn Diagrams show Union and Intersection 8

Simple query language: Boolean – Terms + Connectors (or operators) – terms • words • normalized (stemmed) words • phrases • thesaurus terms – connectors • AND • OR • NOT 9

Boolean Queries • Cat OR Dog • Cat AND Dog • (Cat AND Dog) OR Collar • (Cat AND Dog) OR (Collar AND Leash) • (Cat OR Dog) AND (Collar OR Leash) 10

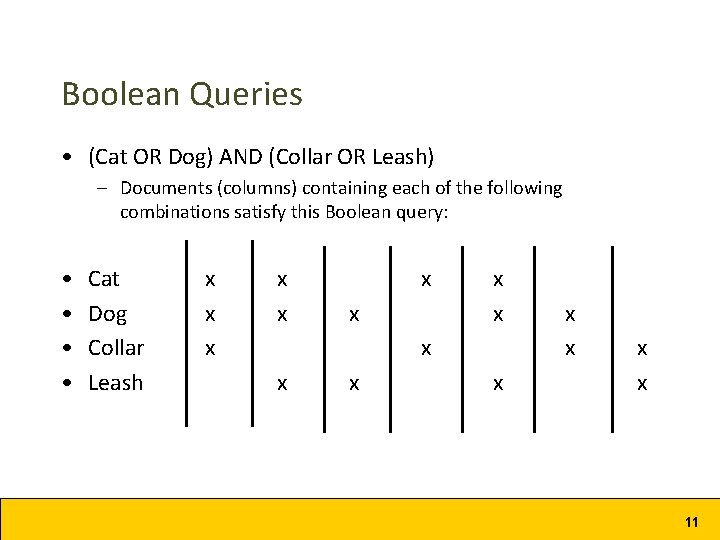
Boolean Queries • (Cat OR Dog) AND (Collar OR Leash) – Documents (columns) containing each of the following combinations satisfy this Boolean query: • • Cat Dog Collar Leash x x x x x 11

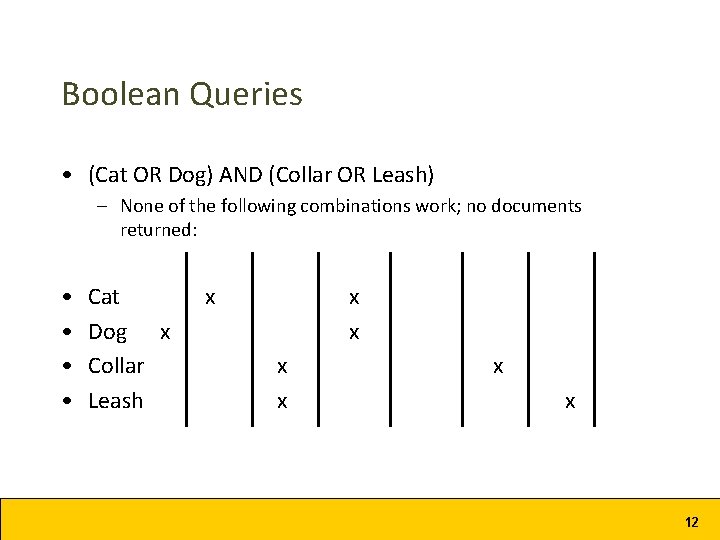
Boolean Queries • (Cat OR Dog) AND (Collar OR Leash) – None of the following combinations work; no documents returned: • • Cat Dog x Collar Leash x x x x 12

Boolean Notation Operator Symbol Example AND * or • or A*B = A • B = AB OR + or U A+B = A U B NOT ¬ or ¯ or - ¬(A+B) = -(A+B) XOR + A + B = AB + AB U 13 U

Boolean Queries – Usually expressed as INFIX operators in IR • ((a AND b) OR (c AND b)) – NOT is UNARY PREFIX operator • ((a AND b) OR (c AND (NOT b))) – AND and OR can be n-ary operators • (a AND b AND c AND d) – Some rules - (De Morgan revisited) • NOT(a) AND NOT(b) = NOT(a OR b) • NOT(a) OR NOT(b)= NOT(a AND b) • NOT(a)) = a 14

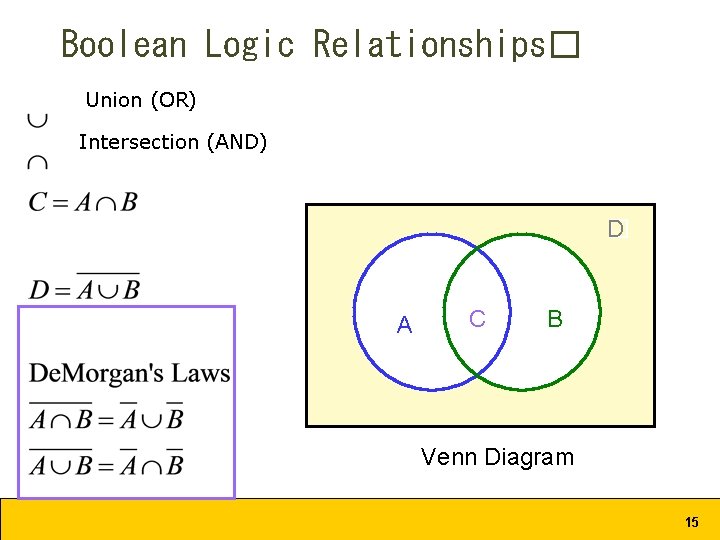
Boolean Logic Relationships� Union (OR) Intersection (AND) D � A C B Venn Diagram 15

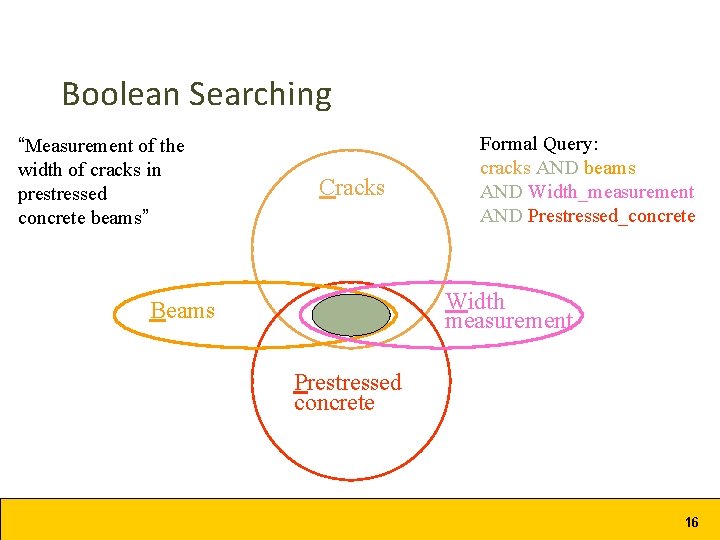
Boolean Searching “Measurement of the width of cracks in prestressed concrete beams” Cracks Formal Query: cracks AND beams AND Width_measurement AND Prestressed_concrete Width measurement Beams Prestressed concrete 16

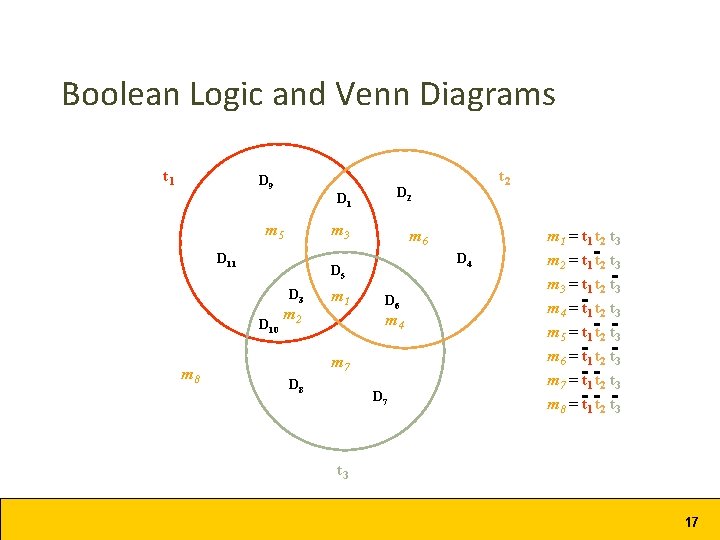
Boolean Logic and Venn Diagrams t 1 D 9 m 3 D 11 m 6 D 4 D 5 D 3 D 10 m 8 D 2 D 1 m 5 m 2 m 1 D 6 m 4 m 7 D 8 t 2 D 7 m 1 = t 1 t 2 t 3 m 2 = t 1 t 2 t 3 m 3 = t 1 t 2 t 3 m 4 = t 1 t 2 t 3 m 5 = t 1 t 2 t 3 m 6 = t 1 t 2 t 3 m 7 = t 1 t 2 t 3 m 8 = t 1 t 2 t 3 17

Boolean Logic and Logic Gates • AND, OR, NOT, NOR, NAND, XOR • Boolean Logic can be expressed as a Logic Gate • Gates are devices that produce the outputs of Boolean operations when given the operations’ input values – Often implemented as electronic circuits called transistors – Provide the building blocks from which computers are constructed • Gates operate on inputs of 0 and 1 • Gates are used to build up circuits that perform computations (e. g. , addition, subtraction), or store values to be used later 18

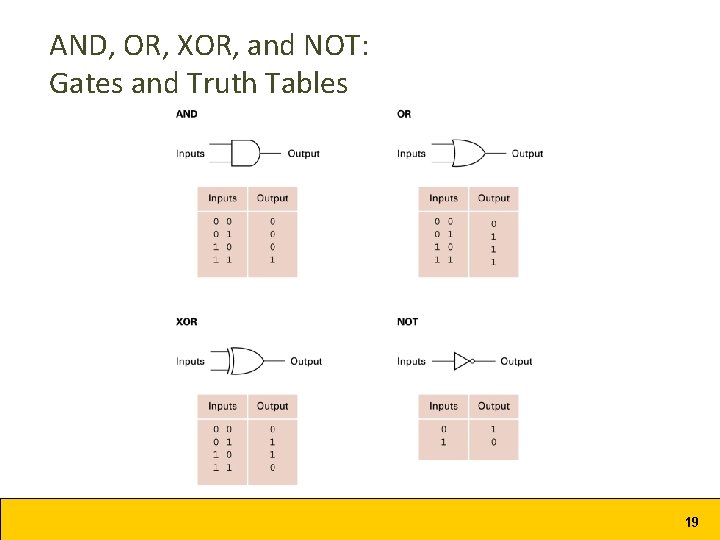
AND, OR, XOR, and NOT: Gates and Truth Tables 19

Exercise • Let’s solve a problem using Boolean Logic – First express the problem using Boolean expressions and/or truth table – Then implement solution using Boolean gates 20

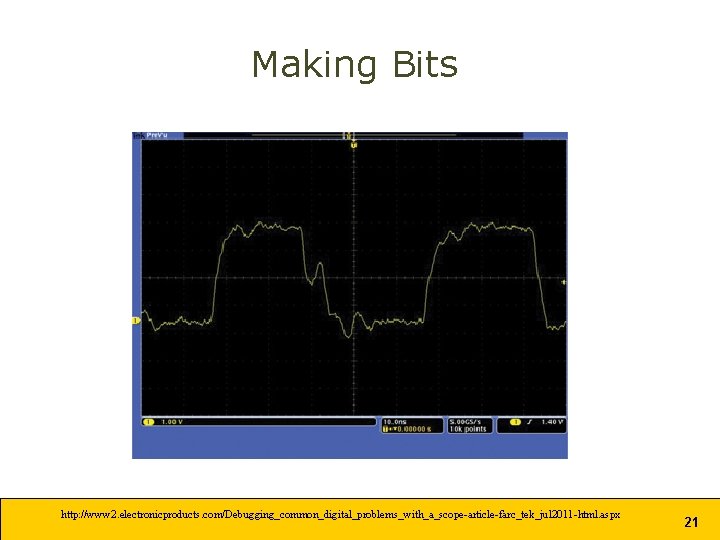
Making Bits http: //www 2. electronicproducts. com/Debugging_common_digital_problems_with_a_scope-article-farc_tek_jul 2011 -html. aspx 21

Making Bits • Digital signals are interpreted by a system as high and low states, – above and below a defined voltage threshold. • In practice, especially at higher speeds, digital signals are rarely ideal with flat high and low levels and clean edge transitions. http: //www 2. electronicproducts. com/Debugging_common_digital_problems_with_a_scope-article-farc_tek_jul 2011 -html. aspx 22

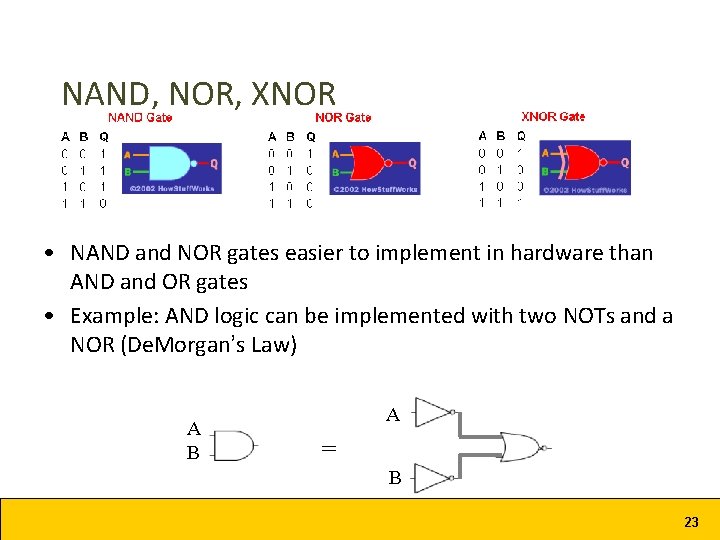
NAND, NOR, XNOR • NAND and NOR gates easier to implement in hardware than AND and OR gates • Example: AND logic can be implemented with two NOTs and a NOR (De. Morgan’s Law) A B A = B 23

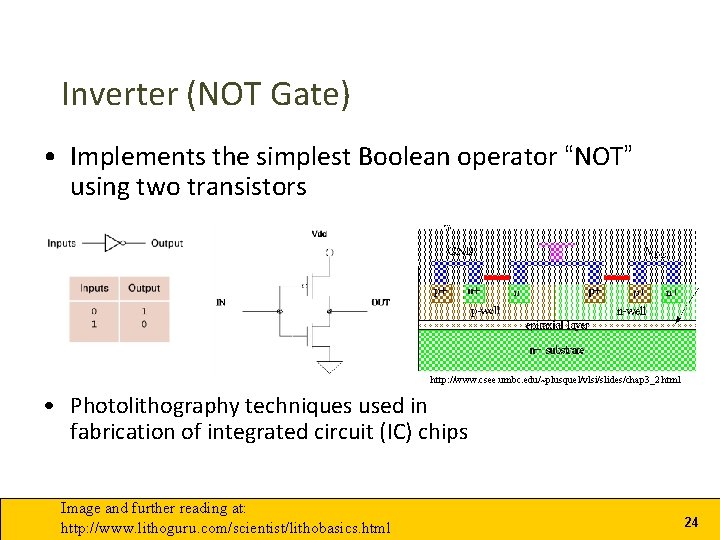
Inverter (NOT Gate) • Implements the simplest Boolean operator “NOT” using two transistors http: //www. csee. umbc. edu/~plusquel/vlsi/slides/chap 3_2. html • Photolithography techniques used in fabrication of integrated circuit (IC) chips Image and further reading at: http: //www. lithoguru. com/scientist/lithobasics. html 24

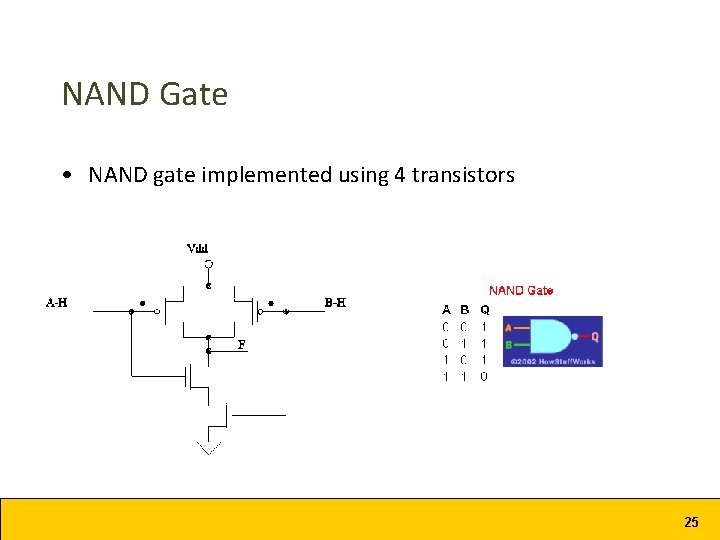
NAND Gate • NAND gate implemented using 4 transistors 25

Integrated Circuit (IC) Chips Contain Gates & Connectors Images from http: //www. ee. ed. ac. uk/~gaa/Digilab. Notes/Digilab/Components/node 7. html 26

LEDs (light-emitting diodes) The circuit can turn the LED on or off. Images from http: //www. cores. ro/electronic/Kit. html 27

Interactive demo of Boolean logic http: //courses. cs. vt. edu/~csonline/Machine. Architecture/Lessons/Gates/index. html 28

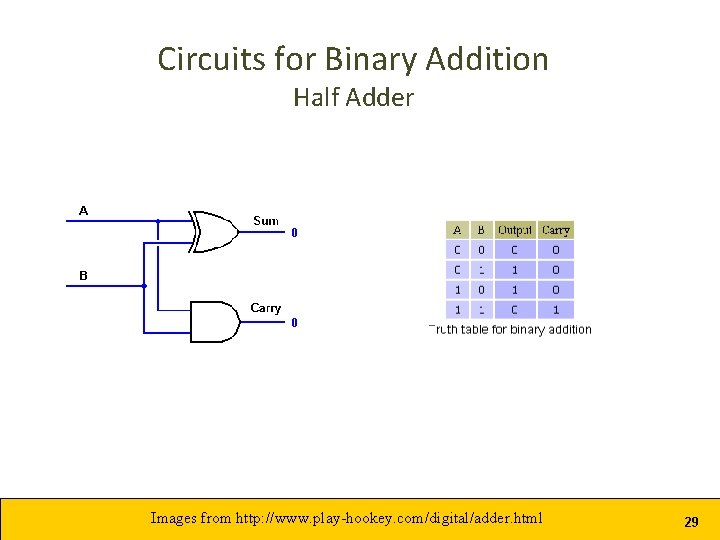
Circuits for Binary Addition Half Adder Images from http: //www. play-hookey. com/digital/adder. html 29

Circuit Board for Half-Adder http: //www. seas. upenn. edu/~ee 111/half-adder/Half-adder. html 30

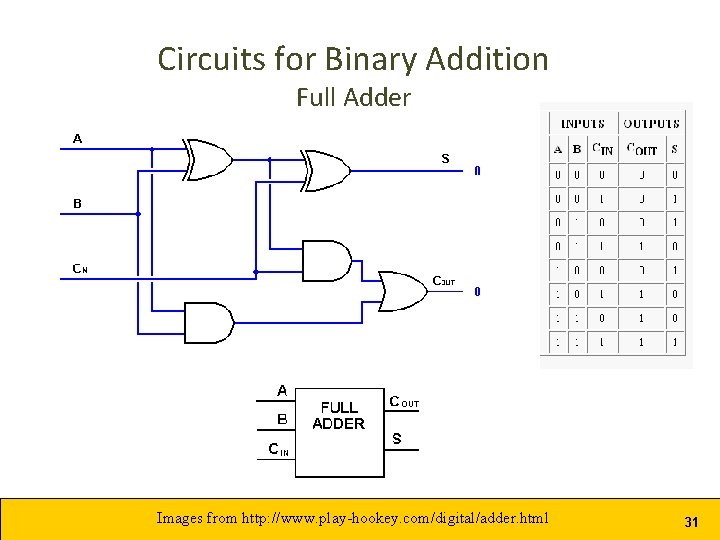
Circuits for Binary Addition Full Adder Images from http: //www. play-hookey. com/digital/adder. html 31

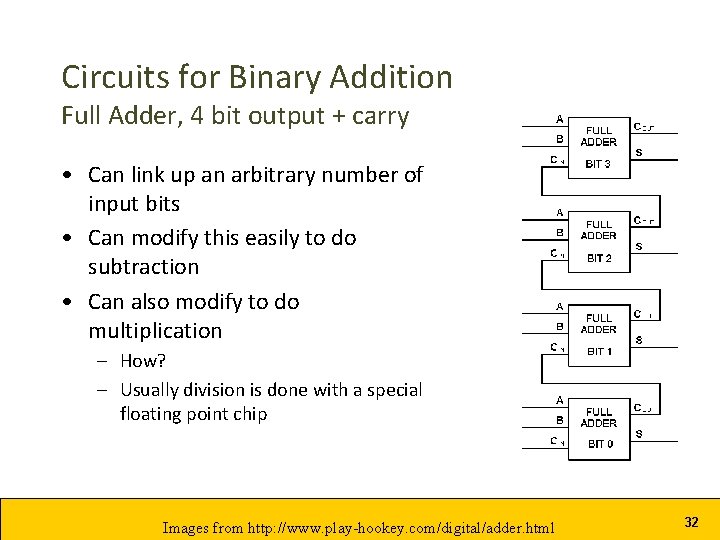
Circuits for Binary Addition Full Adder, 4 bit output + carry • Can link up an arbitrary number of input bits • Can modify this easily to do subtraction • Can also modify to do multiplication – How? – Usually division is done with a special floating point chip Images from http: //www. play-hookey. com/digital/adder. html 32

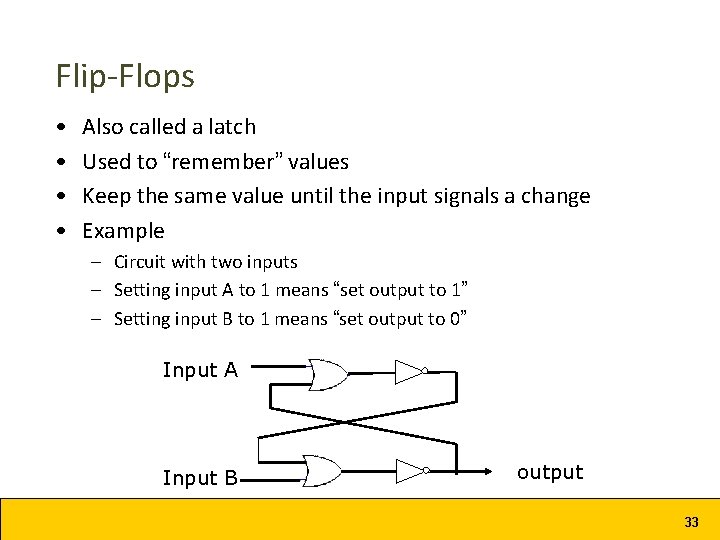
Flip-Flops • • Also called a latch Used to “remember” values Keep the same value until the input signals a change Example – Circuit with two inputs – Setting input A to 1 means “set output to 1” – Setting input B to 1 means “set output to 0” Input A Input B output 33

Simple Flip-Flop: The Problem – If both inputs change simultaneously, the final state of the latch cannot be determined ahead of time. This is called: • A Race Condition: the result depends on which input got changed first. • Nondeterministic: Not being able to predict what will happen with certainty. – Nondeterminism is very, very bad from the perspective of computer science (most of the time). 34

The clock – CPS (cycles per second): • The measure of how frequently an alternating current changes direction. • This term has been replaced by the term hertz (Hz). – gigahertz (GHz): • A unit of frequency denoting 109 Hz. 35

Clock cycles • Logic gates introduce propagation delays as the signal goes through them. • Therefore, a clock cycle is introduced into the circuit. – It’s like a heart beat for the system. • It connects up to all the circuits that need it, so they can all be told to update at the same time. – The clock cycle can be no faster than the slowest set of logic gates. • The clock keeps the circuit running in a predictable fashion, by making sure every part of the circuit gets changes to input at the same time. 36

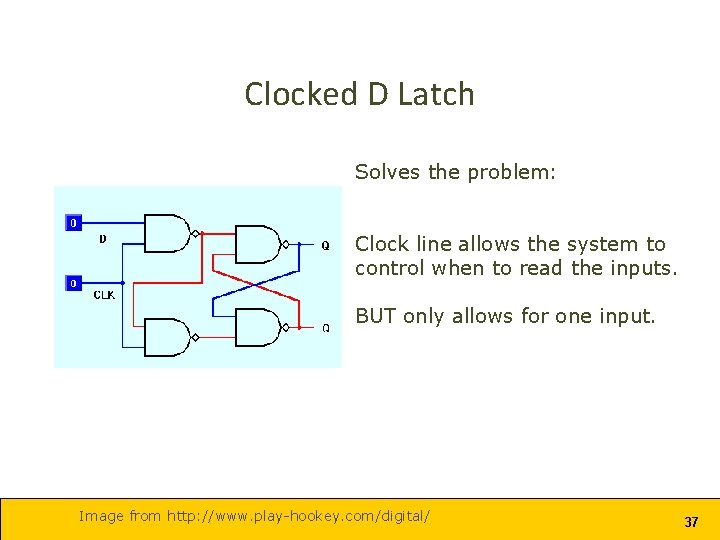
Clocked D Latch Solves the problem: Clock line allows the system to control when to read the inputs. BUT only allows for one input. Image from http: //www. play-hookey. com/digital/ 37

Example; Linking Boolean to Circuits • Lighting up a digital clock How are the LEDS for the digital clock controlled? 38

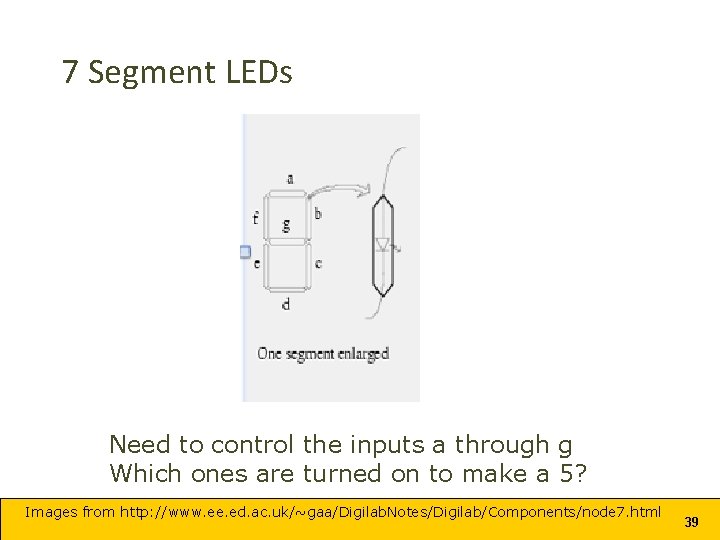
7 Segment LEDs Need to control the inputs a through g Which ones are turned on to make a 5? Images from http: //www. ee. ed. ac. uk/~gaa/Digilab. Notes/Digilab/Components/node 7. html 39

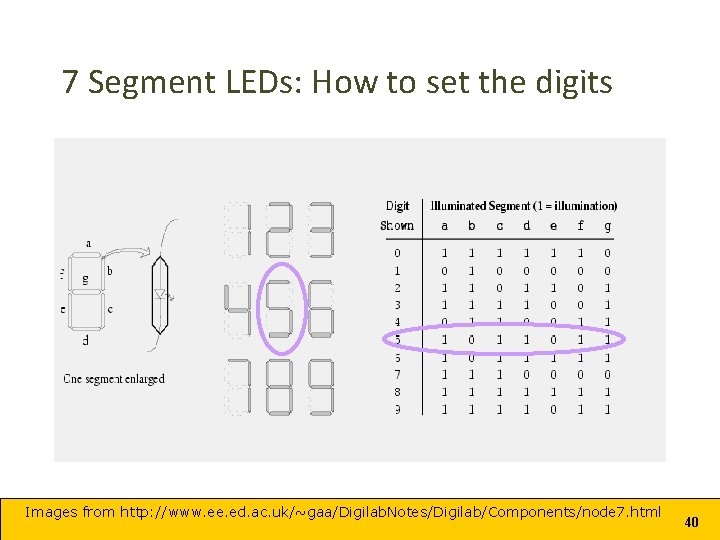
7 Segment LEDs: How to set the digits Images from http: //www. ee. ed. ac. uk/~gaa/Digilab. Notes/Digilab/Components/node 7. html 40

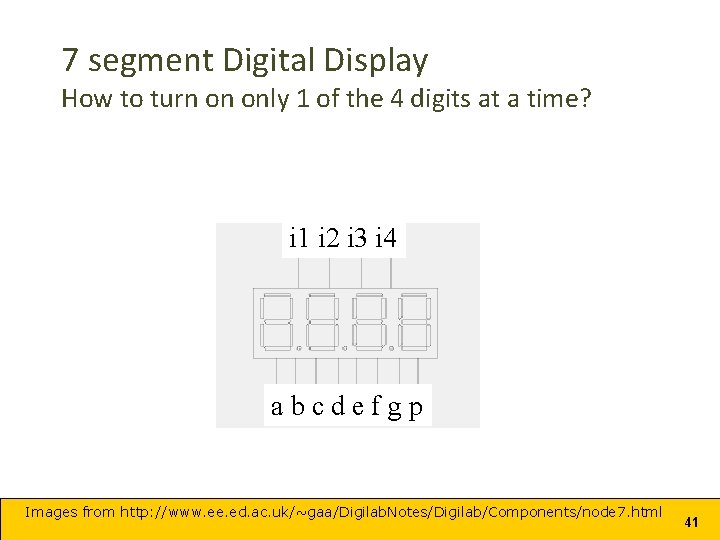
7 segment Digital Display How to turn on only 1 of the 4 digits at a time? i 1 i 2 i 3 i 4 abcdefgp Images from http: //www. ee. ed. ac. uk/~gaa/Digilab. Notes/Digilab/Components/node 7. html 41

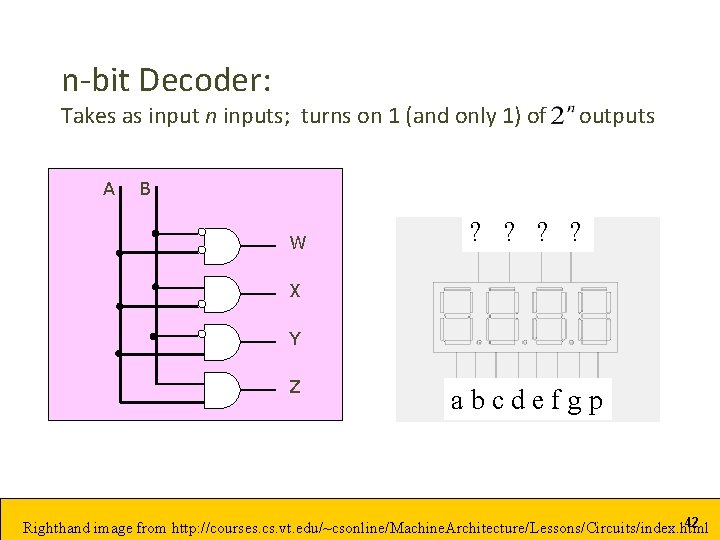
n-bit Decoder: Takes as input n inputs; turns on 1 (and only 1) of A outputs B W ? ? X Y Z abcdefgp 42 Righthand image from http: //courses. cs. vt. edu/~csonline/Machine. Architecture/Lessons/Circuits/index. html

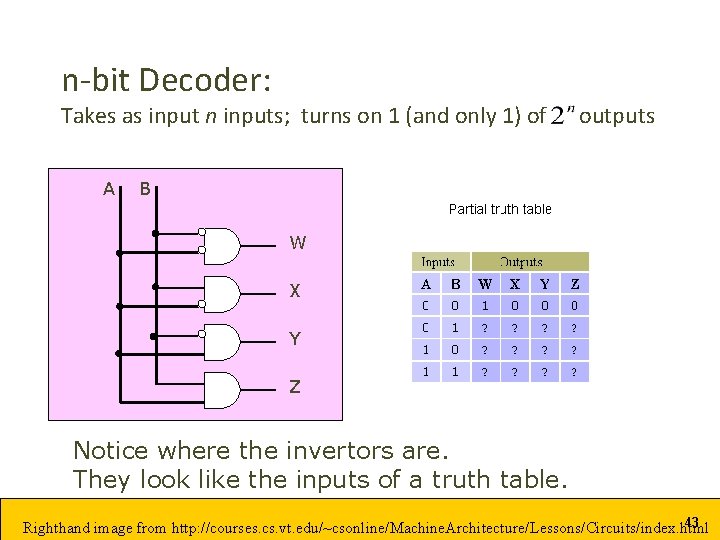
n-bit Decoder: Takes as input n inputs; turns on 1 (and only 1) of A outputs B W X Y Z Notice where the invertors are. They look like the inputs of a truth table. 43 Righthand image from http: //courses. cs. vt. edu/~csonline/Machine. Architecture/Lessons/Circuits/index. html

Summary • Quick Binary Exercise • Boolean Logic – de. Morgan’s Law • How Bits are Made • Relating Boolean Logic to Circuits – Logic gates • Special gates: – Flip Flops – Adders – Decoders • Next time: The CPU and instruction sets!� 44