hypothesis testing with special focus on simulation Hypothesis

hypothesis testing with special focus on simulation Hypothesis Testing for Simulation 1

u Hypothesis Test answers yes/no question with some statistical certainty u H 0 = default hypothesis u Ha = alternate hypothesis Øis a statement Øis the precise opposite Hypothesis Testing for Simulation 2

u. X = test statistic (RANDOM!) Øsufficient (uses all avail. data) Øoften Z, T, N are used as notation u FX ua = its probability distribution = P[reject H 0 | H 0 true] Hypothesis Testing for Simulation 3

uc a = critical region for a ua = P[X in ca | H 0] ua is our (controllable) risk Hypothesis Testing for Simulation 4

TWISTED LOGIC u We WANT to reject H 0 and conclude Ha, so. . . ØWe make a very small, so. . . ØIf we can reject, we have strong evidence that Ha is true u This construct often leads to inconclusive results Ø“There is no significant statistical evidence that. . . ” Hypothesis Testing for Simulation 5

IMPORTANT u. Inability to reject <> H 0 true Hypothesis Testing for Simulation 6

POWER OF THE TEST ub = P[X not in ca | Ha] u 1 -b = P[correctly rejecting] Hypothesis Testing for Simulation 7

VENACULAR ua is type I error ØProbability of incorrectly rejecting ub is type II error ØProbability of incorrectly missing the opportunity to reject Hypothesis Testing for Simulation 8

UNOFFICIAL VENACULAR utype III error – answered the wrong question utype IV error – perfect answer delivered too late Hypothesis Testing for Simulation 9

EXAMPLE! u Dial-up ISP has long experience & knows. . . Hypothesis Testing for Simulation 10

We get DSL, observe 12 samples Hypothesis Testing for Simulation 11

IS DSL FASTER? u. H 0 : m. DSL = 50 u. H a : m. DSL < 50 utest with P[type I] = 0. 01 Hypothesis Testing for Simulation 12

PROBABILITY THEORY u. Z ~ tn-1 Ø Must know the probability distribution of the test statistic IOT construct critical region Hypothesis Testing for Simulation 13

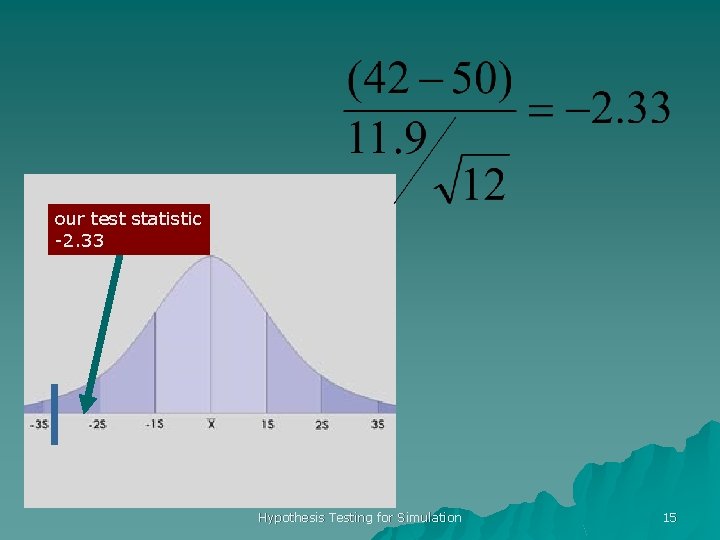
99% of the probability above -2. 718 u for n = 12, a = 0. 01, ca = 2. 718 Hypothesis Testing for Simulation 14

our test statistic -2. 33 Hypothesis Testing for Simulation 15

-2. 33 -2. 718 (0. 021) (0. 01) u 0. 021 -1. 796 (0. 05) called the p-value u Given H 0, we expect to see a test statistic as extreme as Z roughly 2% of the time. Hypothesis Testing for Simulation 16

CONFIDENCE INTERVALS u. For a given a ØP[la <= m <= ua] = 1 -a m Based on the sample So they are RANDOM! la Hypothesis Testing for Simulation ua 17

GOODNESS-OF-FIT TEST u Discrete, categorized data ØRolls of dice ØMiss distances in 5 -ft. increments u H 0 assumes a fully-specified probability model ØHa: the glove does not fit! Hypothesis Testing for Simulation 18

TEST STATISTIC “chi-squared distribution with gnu degrees of freedom” Hypothesis Testing for Simulation 19

un = observations - estimated param u Did you know. . . if Zi~N(0, 1), then Z 12+ Z 22+. . . + Zn 2 ~ cn 2 Hypothesis Testing for Simulation 20

CELLS u. H 0 always results in a set of category cells with expected frequencies u. EXAMPLE ØCoin is tossed 100 times ØH 0: Coin Fair Hypothesis Testing for Simulation 21

CELLS AND EXPECTED FREQUENCIES EXPECT H 50 T 50 Hypothesis Testing for Simulation 22

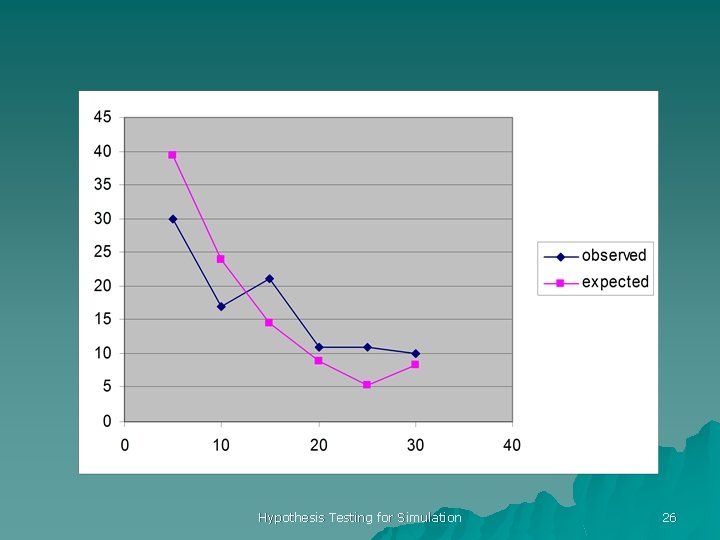
EXAMPLE u. Cannon a target places rounds around ØH 0: miss distance ~ expon(0. 1 m) u. Record data in 5 m intervals Ø(0 -5), (5 -10), . . . (25+) Hypothesis Testing for Simulation 23

EXPONENTIALS E(X)=1/l Hypothesis Testing for Simulation 24

RESULTS RIGHT OBS 1 -exp(-0. 1 x) PROB EXPECT (OBS-EXPECT)^2 0. 00 5. 00 30 0. 39 39. 35 2. 22 10. 00 17 0. 63 0. 24 23. 87 1. 97 15. 00 21 0. 78 0. 14 14. 47 2. 94 20. 00 11 0. 86 0. 09 8. 78 0. 56 25. 00 11 0. 92 0. 05 5. 33 6. 05 30+ 10 1. 00 0. 08 8. 21 0. 39 100. 00 Hypothesis Testing for Simulation 14. 14 25

Hypothesis Testing for Simulation 26

TEST RESULTS u Degrees of Freedom Ø 6 cells Ø 0 parameters estimated Øn = 6 u For the c 62 distribution, the pvalue for 14. 14 is about p=0. 025 u REJECT at any a > 0. 025 Hypothesis Testing for Simulation 27

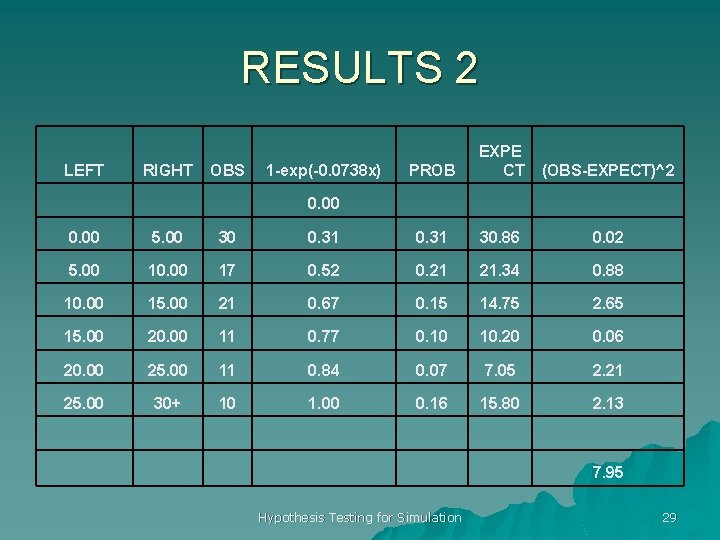
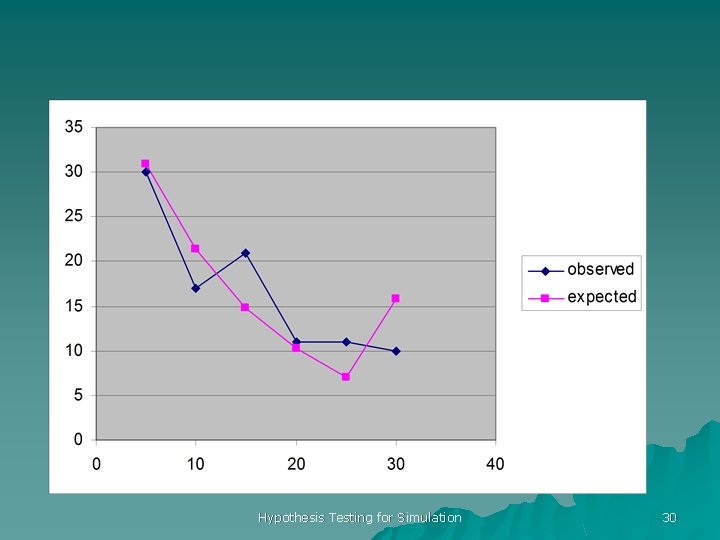
DIFFERENT H 0 u H 0: the miss distances are exponentially distributed u Ha: the exponential shape is incorrect u We estimate the parameter, we lose one degree of freedom Hypothesis Testing for Simulation 28

RESULTS 2 LEFT RIGHT OBS 1 -exp(-0. 0738 x) PROB EXPE CT (OBS-EXPECT)^2 0. 00 5. 00 30 0. 31 30. 86 0. 02 5. 00 10. 00 17 0. 52 0. 21 21. 34 0. 88 10. 00 15. 00 21 0. 67 0. 15 14. 75 2. 65 15. 00 20. 00 11 0. 77 0. 10 10. 20 0. 06 20. 00 25. 00 11 0. 84 0. 07 7. 05 2. 21 25. 00 30+ 10 1. 00 0. 16 15. 80 2. 13 7. 95 Hypothesis Testing for Simulation 29

Hypothesis Testing for Simulation 30

un =5 u p-value 0. 05 for 7. 83 is larger than u CANNOT REJECT u CONCLUSION? Hypothesis Testing for Simulation 31

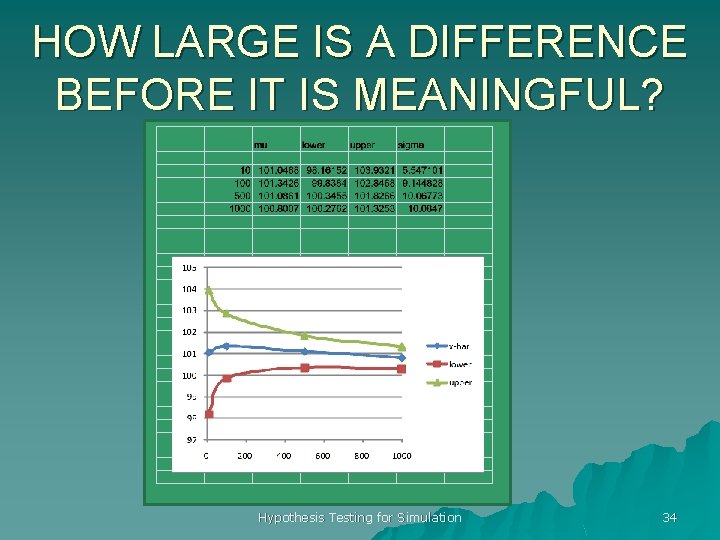
SIMULATION vs. STATISTICS u Statistics Ø Sample is fixed and given Ø Conclusion is unknown Ø Significance is powerful u Simulation Ø Sample is arbitrarily large Ø Conclusion is known Ø We need another thought about what is meaningful Hypothesis Testing for Simulation 32

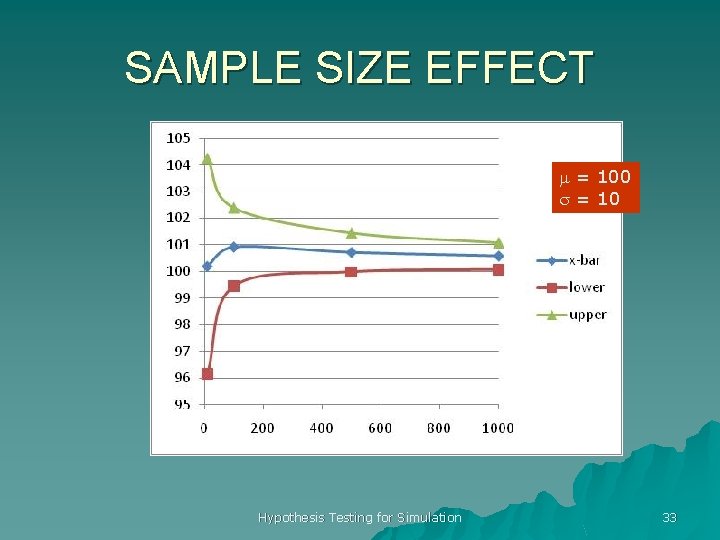
SAMPLE SIZE EFFECT m = 100 s = 10 Hypothesis Testing for Simulation 33

HOW LARGE IS A DIFFERENCE BEFORE IT IS MEANINGFUL? Hypothesis Testing for Simulation 34

SUMMARY u. You probably knew the mechanics of HT u. You might have a new perspective Hypothesis Testing for Simulation 35