Hypothesis Testing pvalue 21312 Randomization distribution pvalue Statistical

Hypothesis Testing: p-value 2/13/12 • Randomization distribution • p-value • Statistical significance Section 4. 2 Professor Kari Lock Morgan Duke University

To Do • Project 1 Proposal (due Wednesday) • Homework 4 (due Monday) NO LATE HOMEWORK ACCEPTED!

Exercise and Pulse In the actual experiment, the people who exercised for 5 seconds had an average pulse of 85. 5. Those who did not exercise had an average pulse of 69. 6. Is this sample difference larger than we would see, just by random chance, if exercising for 5 seconds did not increase pulse rate?

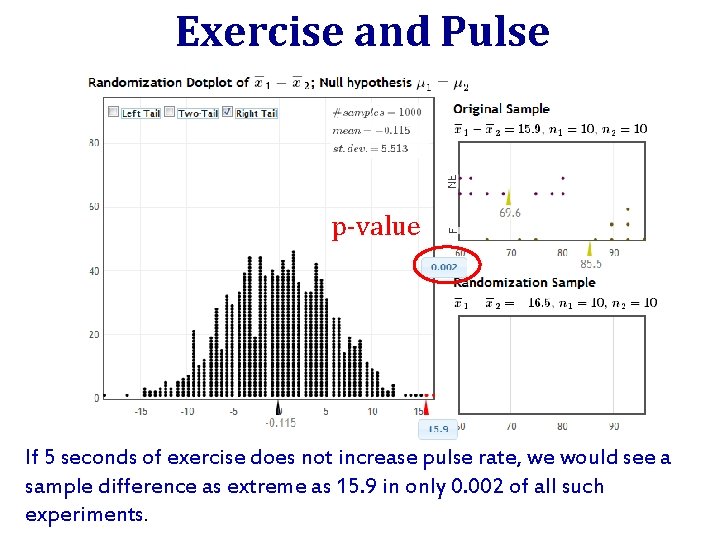
Exercise and Pulse p-value www. lock 5 stat. com/statkey/ If 5 seconds of exercise does not increase pulse rate, we would see a sample difference as extreme as 15. 9 in only 0. 002 of all such experiments.

Cocaine Addiction • In a randomized experiment on treating cocaine addiction, 48 people were randomly assigned to take either Desipramine (a new drug), or Lithium (an existing drug), and then followed to see who relapsed • Question of interest: Is Desipramine better than Lithium at treating cocaine addiction?

Cocaine Addiction • What is the statistic of interest? • What are the hypotheses of this test?

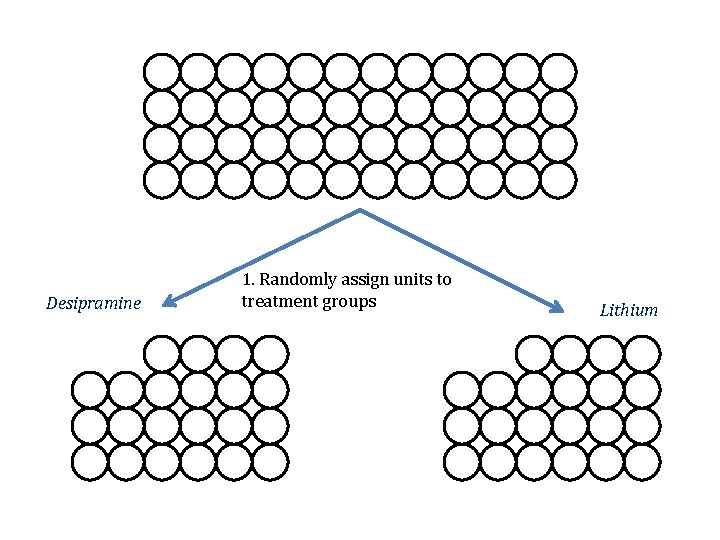
R R R R R R R R R R R R 1. Randomly assign units to treatment groups Desipramine R R Lithium R R R R R R R R R R

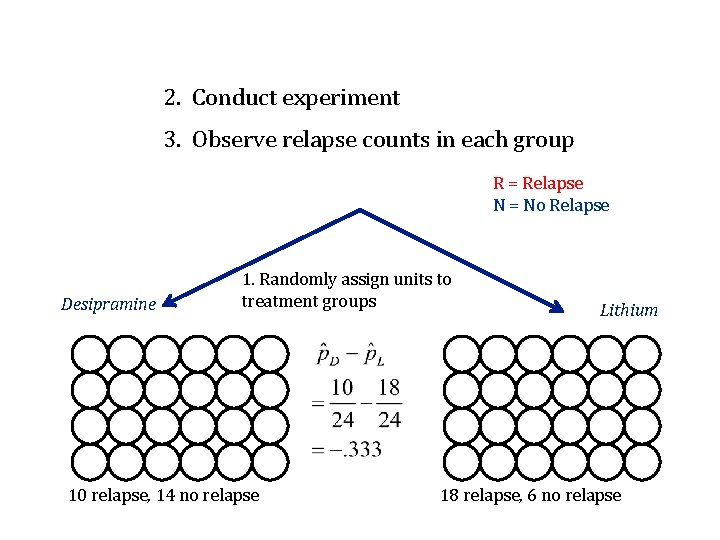
2. Conduct experiment 3. Observe relapse counts in each group R = Relapse N = No Relapse 1. Randomly assign units to treatment groups Desipramine Lithium R R R R N R R R R N R N N R R R N N N 10 relapse, 14 no relapse 18 relapse, 6 no relapse

Cocaine Addiction • Two options: 1. H 0 is true (the drugs cause the same proportion of relapses) 2. Ha is true (Desipramine causes a smaller proportion of relapses than Lithium) • In situation (1), how would you explain the observed difference in the proportion of relapses? • How can we see whether this is a plausible explanation?

Measuring Evidence against H 0 To see if a statistic provides evidence against H 0, we need to see what kind of sample statistics we would observe, just by random chance, if H 0 were true

Randomization Test • Assume the null hypothesis is true • Simulate new randomizations • For each, calculate the statistic of interest • Find the proportion of these simulated statistics that are as extreme as your observed statistic

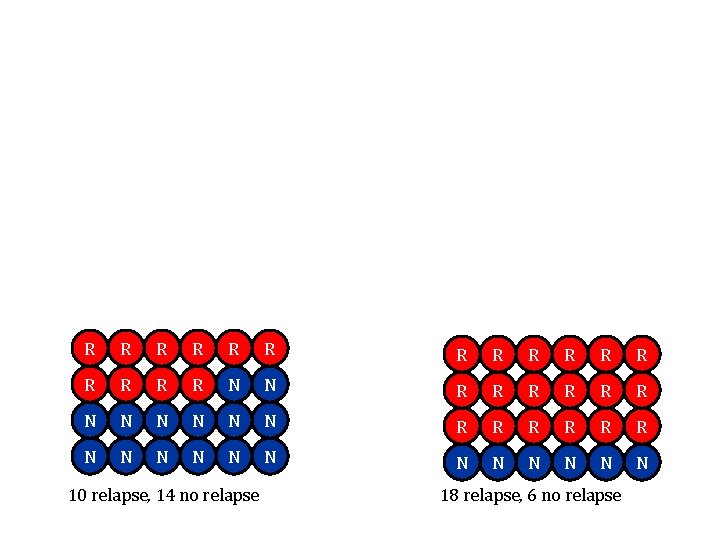
R R R R N N R R R N N N N 10 relapse, 14 no relapse 18 relapse, 6 no relapse

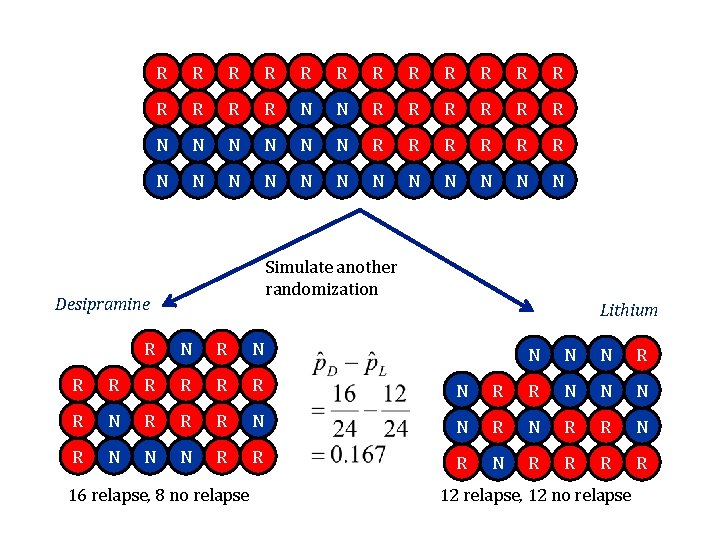
R R R R N N R R R N N N N Simulate another randomization Desipramine Lithium R N N N N R R R R N N N R R R N N N R R R R 16 relapse, 8 no relapse 12 relapse, 12 no relapse

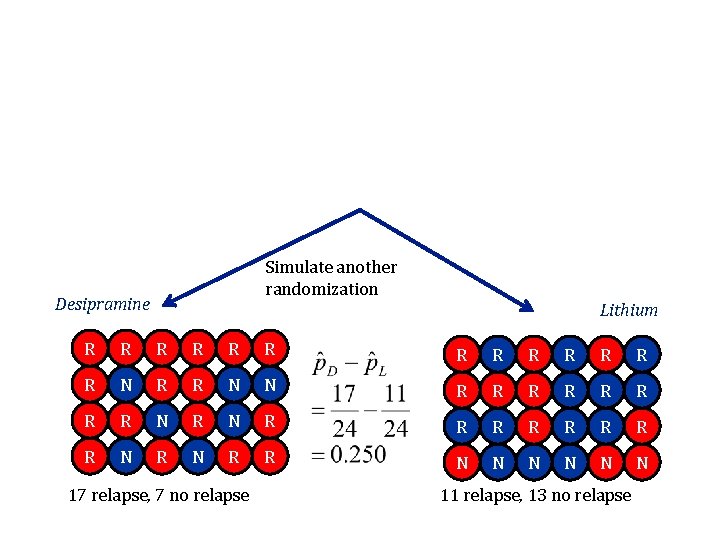
Simulate another randomization Desipramine Lithium R R R R N R R N N R R R R N R N R R N N N 17 relapse, 7 no relapse 11 relapse, 13 no relapse

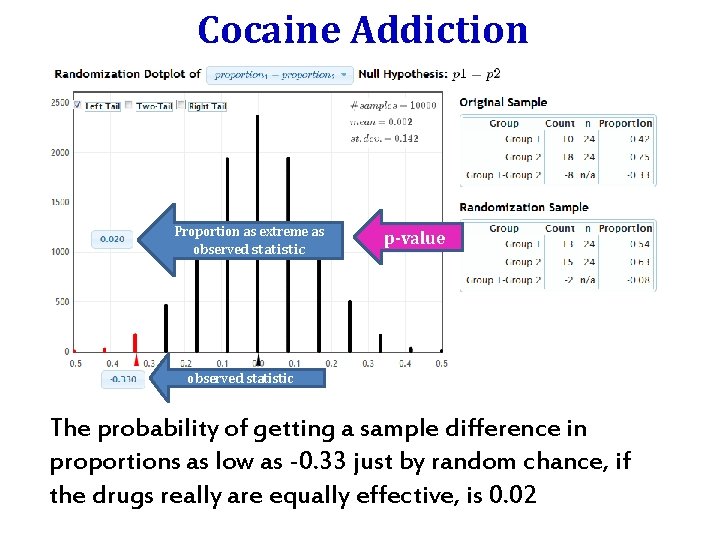
Cocaine Addiction Proportion as extreme as observed statistic p-value www. lock 5 stat. com/statkey observed statistic The probability of getting a sample difference in proportions as low as -0. 33 just by random chance, if the drugs really are equally effective, is 0. 02

p-value • Based on a randomization distribution, the pvalue is the proportion of statistics that are more extreme than that observed • This is the area in the tail(s) beyond the observed statistic in the randomization distribution • Which tail(s) to include depends on the alternative hypothesis

Alternative Hypothesis • A one-sided alternative contains either > or < • A two-sided alternative contains ≠ • The alternative hypothesis depends on the research question of interest • For a one-sided alternative, the p-value is the proportion in the tail specified by Ha • For a two-sided alternative, the p-value is twice the proportion in the smallest tail

Sleep or Caffeine for Memory? • Students were given words to memorize, and then randomly assigned to either take a 90 min nap, or to stay awake and take a caffeine pill. 2 ½ hours later, all students were tested on their recall ability. Is sleep or caffeine better for memory? How extreme would this be if H 0 were true? ? ? Mednick, Cai, Kanady, and Drummond (2008). “Comparing the benefits of caffeine, naps and placebo on verbal, motor and perceptual memory, ” Behavioral Brain Research, 193, 79 -86.

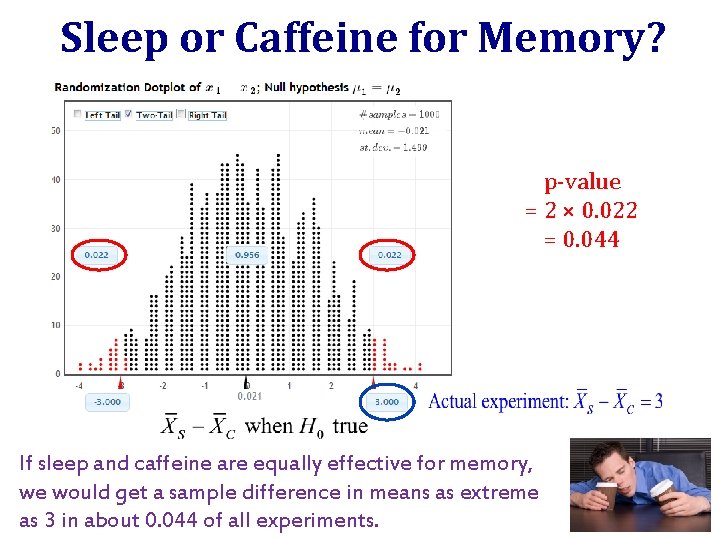
Sleep or Caffeine for Memory? www. lock 5 stat. com/statkey p-value = 2 × 0. 022 = 0. 044 If sleep and caffeine are equally effective for memory, we would get a sample difference in means as extreme as 3 in about 0. 044 of all experiments.

Infections in Childbirth • The Center for Disease Control (CDC) conducted a randomized trial in South Africa in which half of women in labor are randomly assigned to be treated with a wipe containing chlorohexidine, and the other half with a sterile wipe (control) Source: Eriksen, Sweeten, Blanco (1997). “Chlorohexidine vs Sterile Vaginal Wash During Labor to Prevent Peripartum Infection, ” American Journal of Obstetrics and Gynecology, 176: 426 -430.

Infections in Childbirth What can you conclude about the p-value? a) p-value < 0. 5 b) p-value > 0. 5 c) Nothing

Alternative Hypothesis • The p-value is the probability of getting results are extreme as your sample statistic, if the null hypothesis is true • “As extreme as” is defined in the direction of the alternative hypothesis. (for two-sided alternatives, consider both tails) • If your sample statistic does not support your alternative hypothesis, there is no point in going through the test!

p-value What can you conclude about the p-value? a) b) c) d) p-value = 0. 5 p-value = 1 Nothing

p-value What can you conclude about the p-value? a) p-value < 0. 5 b) p-value > 0. 5 c) Nothing

Multiple Sclerosis and Sunlight • It is believed that sunlight offers some protection against multiple sclerosis, but the reason is unknown • To find out, researchers randomly assigned mice to one of three treatments: • Control (nothing) • Vitamin D Supplements • UV Light • All mice were injected with proteins known to induce a mouse form of MS, and they observed which mice got MS Seppa, Nathan. “Sunlight may cut MS risk by itself”, Science News, April 24, 2010 pg 9, reporting on a study appearing March 22, 2010 in the Proceedings of the National Academy of Science.

Multiple Sclerosis and Sunlight • In testing whether UV light provides protection against MS in mice, what are the null and alternative hypotheses? p. UV = proportion of mice exposed to UV light that get MS p. C = proportion of mice not exposed to UV light that get MS a) b) c) d) H 0 : p. UV – p. C > 0, < 0, = 0, Ha: p. UV – p. C =0 =0 >0 <0

Multiple Sclerosis and Sunlight • In testing whether UV light provides protection against MS in mice, the experiment yielded a p-value of 0. 002. What would you conclude? a) H 0 is probably not true UV light does provide protection against MS b) H 0 is probably not true UV light does not provide protection against MS c) Ha is probably not true UV light does provide protection against MS d) Ha is probably not true UV light does not provide protection against MS e) Nothing

Multiple Sclerosis and Sunlight • In testing whether Vitamin D provides protection against MS in mice, the experiment yielded a p-value of 0. 47. What would you conclude? a) H 0 is probably not true Vitamin D does provide protection against MS b) H 0 is probably not true Vitamin D does not provide protection against MS c) Ha is probably not true Vitamin D does provide protection against MS d) Ha is probably not true Vitamin D does not provide protection against MS e) Nothing

Strength of Evidence • The p-value is the probability of getting results as extreme as those observed, if the null hypothesis is true • The p-value measures evidence against the null hypothesis p-value

p-value The smaller thep-value, The smaller the p-value, the stronger the evidence against H o. the stronger the evidence the stronger the against H. o evidence against H o.

Hypothesis Testing • If the p-value is small enough, we reject the null hypothesis, in favor of the alternative hypothesis How small is small enough?

Statistical Significance • The significance level, , is the threshold below which the p-value is deemed small enough to reject the null hypothesis • If the p-value is less than , the results are statistically significant, and we reject the null hypothesis in favor of the alternative

Statistical Significance www. xkcd. com

Formal Decisions For a given significance level, , p-value < Reject Ho p-value > Do not Reject Ho

Statistical Conclusions Strength of evidence against H 0: Formal decision of hypothesis test, based on = 0. 05 :

Formal Decisions A formal hypothesis test has only two possible conclusions: 1. The p-value is small: reject the null hypothesis in favor of the alternative 2. The p-value is not small: do not reject the null hypothesis

Elephant Example • Example: H 0 : X is an elephant Ha : X is not an elephant Would you conclude, if you get the following data? • X has four legs • X walks on two legs

Summary • A randomization distribution shows the distribution of statistics that would be observed if H 0 were true • A p-value is the probability of getting a statistic as extreme as that observed, if H 0 is true • The p-value measures the strength of evidence against the null hypothesis Results are statistically significant if the p-value is less than the significance level, α • • In making formal decisions, reject H 0 if the p-value is less than α, otherwise do not reject H 0