Hypothesis Testing Introduction to Inductive Statistics Background Website

Hypothesis Testing Introduction to Inductive Statistics

Background Website • http: //www. intuitor. com/statistics/T 1 T 2 Erro rs. html

Terms • Descriptive Statistics: what we’ve done so far… • Inductive Statistics: making decisions on the basis of statistical evidence • Hypothesis: the relationship or proposition you wish to test, stated to affirm the relationship or proposition • Null Hypothesis: the negative form of the proposition to be tested

Some propositions… • Statistics is making decisions on the basis of incomplete or imperfect information. • A hypothesis or proposition can be refuted by one observation but not proved by many. • We thus proceed by determining the likelihood that the null hypothesis can be rejected.

The Dilemma… There is always the possibility of making the wrong decision: – Rejecting a true hypothesis: Type 1 Error – Failing to reject a false hypothesis: Type 2 Error

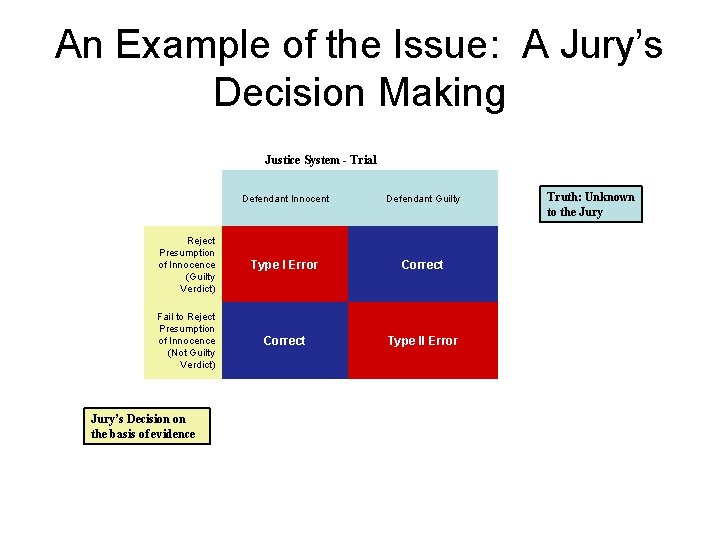
An Example of the Issue: A Jury’s Decision Making Justice System - Trial Defendant Innocent Defendant Guilty Reject Presumption of Innocence (Guilty Verdict) Type I Error Correct Fail to Reject Presumption of Innocence (Not Guilty Verdict) Correct Type II Error Jury’s Decision on the basis of evidence Truth: Unknown to the Jury

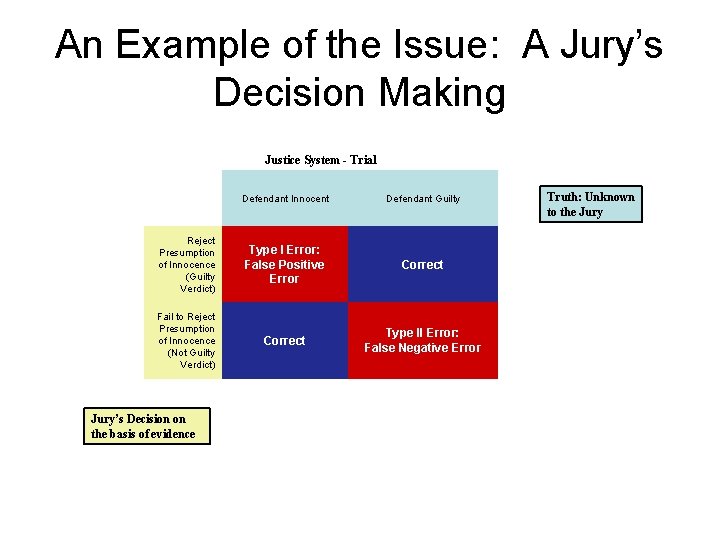
An Example of the Issue: A Jury’s Decision Making Justice System - Trial Defendant Innocent Defendant Guilty Reject Presumption of Innocence (Guilty Verdict) Type I Error: False Positive Error Correct Fail to Reject Presumption of Innocence (Not Guilty Verdict) Correct Type II Error: False Negative Error Jury’s Decision on the basis of evidence Truth: Unknown to the Jury

The Statistical Decision Making Framework Statistics - Hypothesis Test Reject Null Hypothesis Fail to Reject Null Hypothesis Researcher’s Decision Null Hypoth True Null Hypoth False Type I Error Correct Type II Error Unknown Truth

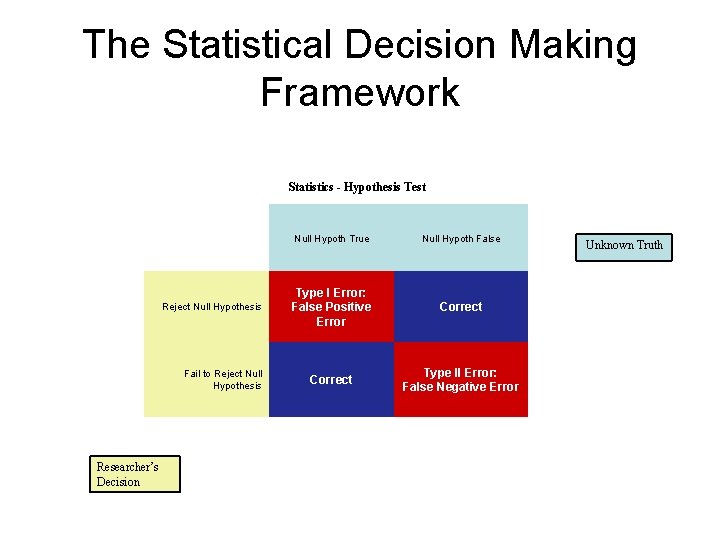
The Statistical Decision Making Framework Statistics - Hypothesis Test Reject Null Hypothesis Fail to Reject Null Hypothesis Researcher’s Decision Null Hypoth True Null Hypoth False Type I Error: False Positive Error Correct Type II Error: False Negative Error Unknown Truth

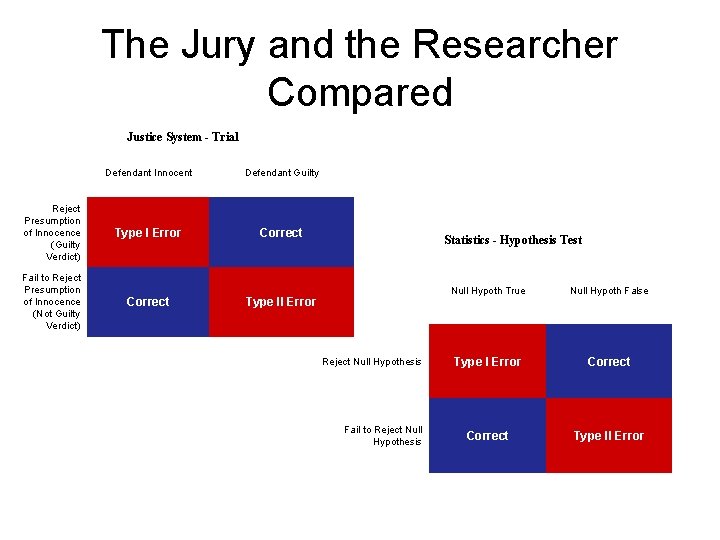
The Jury and the Researcher Compared Justice System - Trial Defendant Innocent Defendant Guilty Reject Presumption of Innocence (Guilty Verdict) Type I Error Correct Fail to Reject Presumption of Innocence (Not Guilty Verdict) Correct Type II Error Statistics - Hypothesis Test Reject Null Hypothesis Fail to Reject Null Hypothesis Null Hypoth True Null Hypoth False Type I Error Correct Type II Error

Steps for Making a Decision • Specify a hypothesis and the null hypothesis • Specify a level of probability which you will use to decide whether to reject the null hypothesis. • Specify the test statistic and the sampling distribution you will use to make a decision. • Calculate the statistics and compare to theoretical probability distribution, for example, the t distribution. • Interpret the results.

General Form of the Test for a Mean • Z tests: – (Sample mean – population mean) / SE of sample mean, or – (Sample mean – population mean)/ (s / √n) • T tests: – (Sample mean – population mean) / SE of sample mean, or – (Sample mean – population mean)/ (s / √n-1)

General Form of a T Test • t = sample estimate – null hypothesis/ SE • Which simplifies to: • t = sample estimate/SE • When the null hypothesis is that the sample statistic is 0.

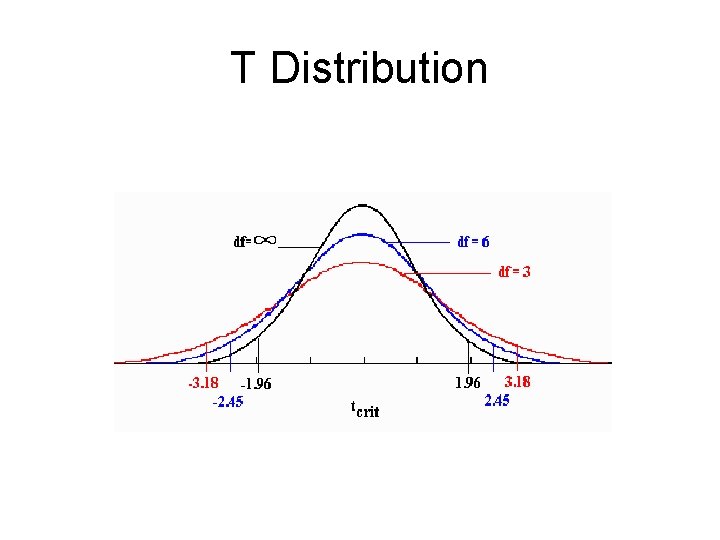
T Distribution

Example 1 • Hypothesis: There is a difference in the average number of persons per household in the 18 th and the 14 th wards. • Null Hypothesis: There is no difference in the average number of persons per household in the 18 th and the 14 th wards, or more specifically, any difference we measure is a matter of the particular sample we have.

Example, cont. • Level of probability: 95% confidence level, so that only 1 in 20 times would the results be different. • Test statistic: Means and a T-Test of the difference of two groups. • t = (mean 1 – mean 2)/ (SE of the difference of mean 1 -mean 2) • Calculate the statistics….

Results Two-sample t test on PERSONS grouped by WARD Group 14 18 N 316 120 Mean 8. 15 5. 25 SD 3. 70 2. 55 Separate Variance t = Difference in Means = 9. 29 df = 310. 5 Prob = 0. 00 2. 90 95. 00% CI = 2. 29 to 3. 52 Pooled Variance t = Difference in Means = 7. 90 df = 434 Prob = 0. 00 2. 90 95. 00% CI = 2. 18 to 3. 62

Results, Graphically Displayed

Interpret the Results • Let’s look at the t distribution again. • We can reject the null hypothesis that the two means are the same in the underlying population (the unknown truth). • We say that there is a statistically significant difference between the average number of persons in the two wards.

Example 2 • Hypothesis: There is a difference in the average number of persons per household in the 18 th and the 20 th wards. • Null Hypothesis: There is no difference in the average number of persons per household in the 18 th and the 20 th wards, or more specifically, the difference is a matter of the particular sample we have.

Results… TEST PERSONS * WARD Data for the following results were selected according to: (WARD<> 14) AND (ward<> 22) Two-sample t test on PERSONS grouped by WARD Group 18 20 N 120 342 Mean 5. 25 5. 72 SD 2. 55 2. 62 Separate Variance t = Difference in Means = -1. 73 df = 213. 5 Prob = 0. 08 -0. 47 95. 00% CI = -1. 01 to 0. 07 Pooled Variance t = Difference in Means = -1. 71 df = 460 Prob = 0. 09 -0. 47 95. 00% CI = -1. 02 to 0. 07

Results, Graphically Displayed…

Interpret the Results • We cannot reject the null hypothesis that the two means are the same in the underlying population (the unknown truth). • We say that there is not a statistically significant difference between the average number of persons in the two wards.

An example of the issue: A jury’s decision making Justice System - Trial Defendant Innocent Defendant Guilty Reject Presumption of Innocence (Guilty Verdict) Type I Error Correct Fail to Reject Presumption of Innocence (Not Guilty Verdict) Correct Type II Error