Hypothesis Testing for Population Means and Proportions Topics

Hypothesis Testing for Population Means and Proportions

Topics • Hypothesis testing for population means: – z test for the simple case (in last lecture) – z test for large samples – t test for small samples for normal distributions • Hypothesis testing for population proportions: – z test for large samples

z-test for Large Sample Tests • We have previously assumed that the population standard deviationσis known in the simple case. • In general, we do not know the population standard deviation, so we estimate its value with the standard deviation s from an SRS of the population. • When the sample size is large, the z tests are easily modified to yield valid test procedures without requiring either a normal population or known σ. • The rule of thumb n > 40 will again be used to characterize a large sample size.

z-test for Large Sample Tests (Cont. ) • Test statistic: • Rejection regions and P-values: – The same as in the simple case • Determination of β and the necessary sample size: – Step I: Specifying a plausible value of σ – Step II: Use the simple case formulas, plug in theσ estimation for step I.

t-test for Small Sample Normal Distribution • z-tests are justified for large sample tests by the fact that: A large n implies that the sample standard deviation s will be close toσfor most samples. • For small samples, s and σare not that close any more. So z -tests are not valid any more. • Let X 1, …. , Xn be a simple random sample from N(μ, σ). μ and σ are both unknown, andμ is the parameter of interest. • The standardized variable

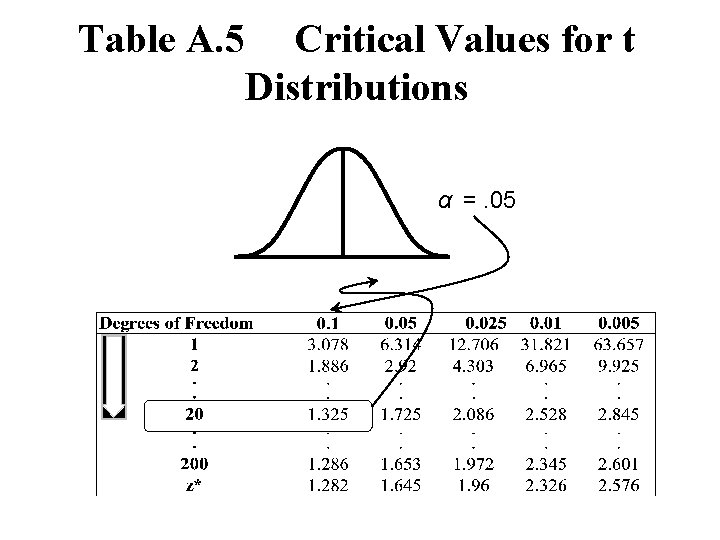
The t Distribution • Facts about the t distribution: – Different distribution for different sample sizes – Density curve for any t distribution is symmetric about 0 and bell-shaped – Spread of the t distribution decreases as the degrees of freedom of the distribution increase – Similar to the standard normal density curve, but t distribution has fatter tails – Asymptotically, t distribution is indistinguishable from standard normal distribution

Table A. 5 Critical Values for t Distributions α =. 05

t-test for Small Sample Normal Distribution (Cont. ) • To test the hypothesis H 0: μ = μ 0 based on an SRS of size n, compute t test statistic • When H 0 is true, the test statistic T has a t distribution with n -1 df. • The rejection regions and P-values for the t tests can be obtained similarly as for the previous cases.

Recap: Population Proportion • Let p be the proportion of “successes” in a population. A random sample of size n is selected, and X is the number of “successes” in the sample. • Suppose n is small relative to the population size, then X can be regarded as a binomial random variable with

Recap: Population Proportion (Cont. ) • We use the sample proportion the population proportion. • We have as an estimator of • Hence is an unbiased estimator of the population proportion.

Recap: Population Proportion (Cont. ) • When n is large, is approximately normal. Thus is approximately standard normal. • We can use this z statistic to carry out hypotheses for H 0: p = p 0 against one of the following alternative hypotheses: – Ha : p > p 0 – H a: p < p 0 – H a: p ≠ p 0

Large Sample z-test for a Population Proportion • The null hypothesis H 0: p = p 0 • The test statistic is Alternative Hypothesis Ha: p > p 0 P-value P(Z ≥ z) Rejection Region for Level α Test z ≥ zα Ha: p < p 0 P(Z ≤ z) z ≤ - zα Ha: p ≠ p 0 2 P(Z ≥ | z |) | z | ≥ zα/2

Determination of β • To calculate the probability of a Type II error, suppose that H 0 is not true and that p = p �instead. Then Z still has approximately a normal distribution but , • The probability of a Type II error can be computed by using the given mean and variance to standardize and then referring to the standard normal cdf.

Determination of the Sample Size • If it is desired that the level αtest also have β(p�) = β for a specified value of β, this equation can be solved for the necessary n as in population mean tests.