Hypothesis testing Descriptive statistics Inferential statistics Allow us

Hypothesis testing Descriptive statistics Inferential statistics Allow us to make statements about a population based on info from samples of population

Hypothesis testing Systematic model: summarises evidence from sampling Can now decide between possible hypotheses Null hypothesis = HO States: no difference between two items Alternate hypothesis = HA States: the two items are different Hypotheses stated in terms of population parameters

Hypothesis testing e. g. Is there a difference between the heights of students at UWC and at Wits? HO: there is no difference in the average height of the two groups of students HA: there is a difference in the average height between the two groups of students. Find: there is a difference in average height. Two possibilities: populations are indeed different or difference is due to random error

Hypothesis testing Q: how much difference is there in the sample?

Hypothesis testing What is the probability of obtaining this much difference just by chance if we have sampled populations that are not different? i. e. , is HO correct? Probability = alpha (α) probability If α probability of the statistic is > 0. 05, then fail to reject H O If α probability of the statistic is ≤ 0. 05, then reject HO.

Hypothesis testing When rejecting, or failing to reject a HO, we could be making one of two errors: Type I error: conclude there is a difference when there is not a difference α probability Type II error: fail to find a difference that actually exists β probability Only way to decrease both α and β is to increase your sample size.

Hypothesis testing Reasoning of hypothesis testing 1. Make a statement (the null hypothesis) about some unknown population parameter. 2. Collect some data. 3. Assuming the null hypothesis is true, what is the probability of obtaining data such as ours? (this is the “p-value”). 4. If this probability is small, then reject the null hypothesis.

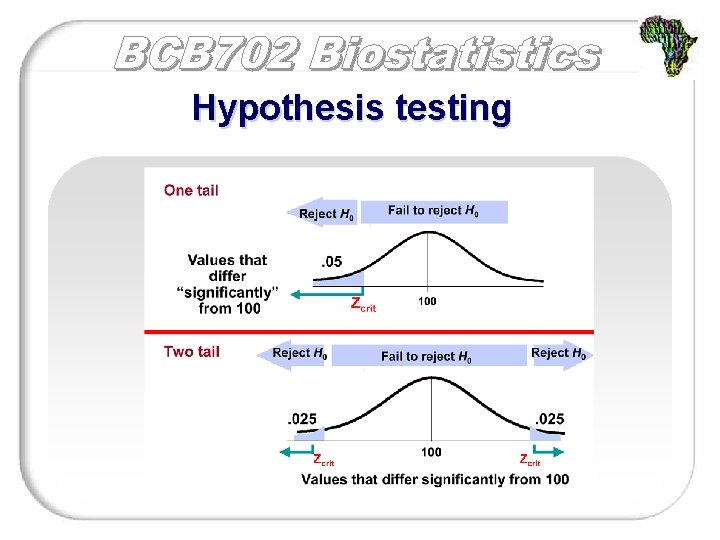
Hypothesis testing Stating hypotheses One-sided Two-sided H 0: µ=110 H 0: µ = 110 HA: µ < 110 HA: µ ≠ 110

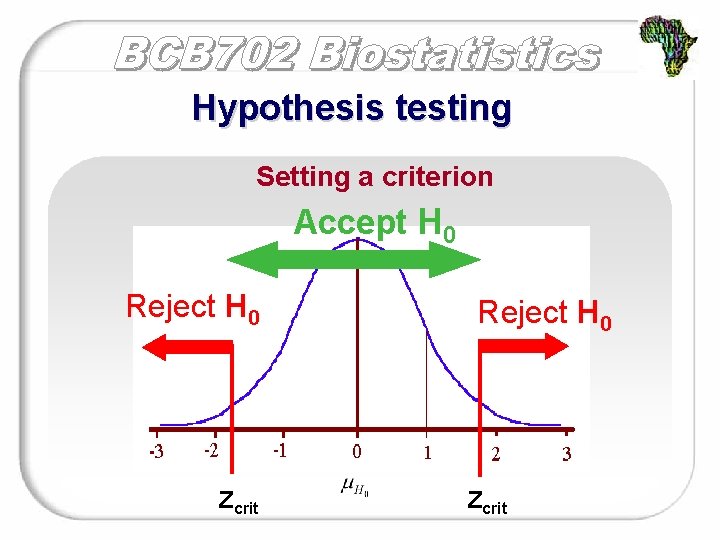
Hypothesis testing Setting a criterion Decide what p-value would be “too unlikely” (the alpha level). The retention region. The range of sample mean values that are “likely” if H 0 is true. If your sample mean is in this region, retain the null hypothesis The rejection region. The range of sample mean values that are “unlikely” if H 0 is true. If your sample mean is in this region, reject the null hypothesis

Hypothesis testing Setting a criterion

Hypothesis testing Computing sample statistics A test statistic (e. g. Ztest, Ttest, or Ftest) is information we get from the sample that we use to make the decision to reject or keep the null hypothesis. A test statistic converts the original measurement (e. g. a sample mean) into units of the null distribution (e. g. a z-score), so that we can look up probabilities in a table.

Hypothesis testing Setting a criterion Accept H 0 Reject H 0 Zcrit

Hypothesis testing Making a decision

Hypothesis testing

Hypothesis testing

Hypothesis testing

Hypothesis testing

Hypothesis testing

Hypothesis testing

Progress assessment By now, you should be able to answer the following questions: • Do I understand all the terms dealt with in the chapter on definitions? • What are the different types of data, and how are they represented? • What is the difference between descriptive and inferential statistics? • What is the difference between a sample and a population? • What is the difference between design structure and treatment structure? • What is a measure of location, and which is the most commonly used? • What are the most commonly used measures of dispersion, and can I use the formulas in order to calculate them? • What is the normal curve, and which parameters define it?

Progress assessment Q’s cont. • How is the normal curve used in order to determine probability? • What is a Z score and Z dispersion? • What are we doing when we are hypothesis testing? • What is the difference between Type I and Type II errors? • How do we use Z scores in order to reject or fail to reject the null hypothesis? • What is the difference between a one-tailed and a two-tailed test?