HYPOTHESIS TESTING ABOUT TWO DEPENDENT POPULATIONS 1 Two

HYPOTHESIS TESTING: ABOUT TWO DEPENDENT POPULATIONS 1

Two Dependent Populations üThe significance test for mean difference in paired (two dependent) populations üWilcoxon Signed Ranks Test üThe Significance Test for The Difference Between Two Dependent Population Proportions ü 2*2 Chi Square Tests for Paired Populations 2

Significance test for mean difference in paired populations A method frequently used for assessing the effectiveness of a treatment or experimental procedure is one that makes use of related observations resulting from non-independent samples. A hypothesis test based on this type of data is known as a paired comparisons test. Related or paired observations may be obtained in a number of ways. The same subjects may be measured before and after receiving some treatment or same subjects can be evaluated at two different conditions. Instead of performing the analysis with individual observations, we use the difference between individual pairs of observations as the variable of interest. 3

(1) H 0: d = 0 H a: d 0 (2) H 0: d = 0 H a: d> 0 (3) H 0: d = 0 H a: d < 0 When the sample differences constitute a simple random sample from a normally distributed population of differences, the test statistic for testing hypotheses about the population mean differences d is Population variance of the differences is known Where Population variance of the differences is unknown is the sample mean difference 4

Example Twelve subjects participated in an experiment to study the effectiveness of a certain diet, combined with a program of exercise, in reducing serum cholesterol levels. The serum cholestrol levels for 12 subjects at the beginning of the program (Before) and at the end of the program (After) are shown in the table. Is the diet program effective? 5

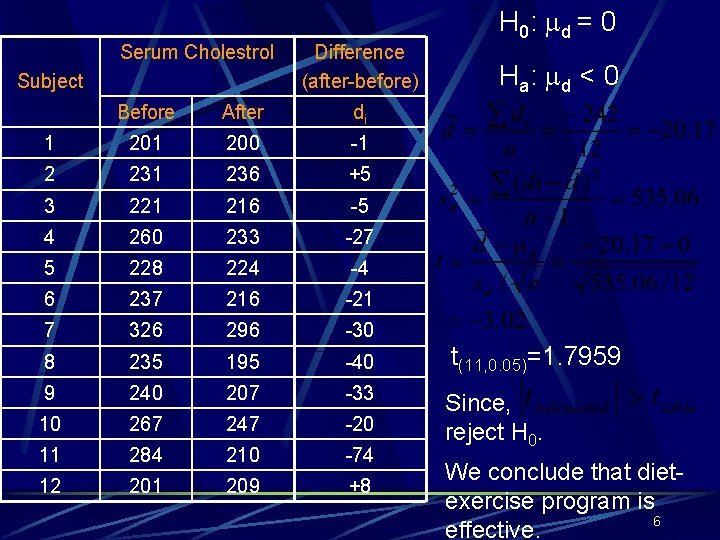
Serum Cholestrol Subject Difference (after-before) H 0: d = 0 H a: d < 0 Before After di 1 200 -1 2 231 236 +5 3 221 216 -5 4 260 233 -27 5 228 224 -4 6 237 216 -21 7 326 296 -30 8 235 195 -40 t(11, 0. 05)=1. 7959 9 240 207 -33 10 267 247 -20 11 284 210 -74 Since, reject H 0. 12 201 209 +8 We conclude that dietexercise program is 6 effective.

Wilcoxon Signed Ranks Test is a nonparametric alternative for the significance test for mean difference in paired samples. It is used with paired data that are measured on at least the ordinal scale and is especially effective when the sample size is small and distribution of the data to be examined does not meet the assumptions of normality, as is required in paired t test. 7

T: The sum of positive or negative ranks, depending on the proposed alternative hypothesis n: The number of positive and negative ranks, excluding ties. Calculation of T statistic: • Take the difference between two measurements for each subject. • New values are ranked by taking absolute values. A. When sample size is smaller than 25, T statistic is used B. When sample size is larger than or equal to 25, z statistic is used. 8

Example Activity scores of 12 subjects before and after the treatment are given: Before 62 27 38 54 33 41 46 30 30 41 44 61 After 68 33 45 56 38 41 54 36 26 40 45 61 Is there any difference between before treatment and after treatment activity scores of 12 subjects? 9

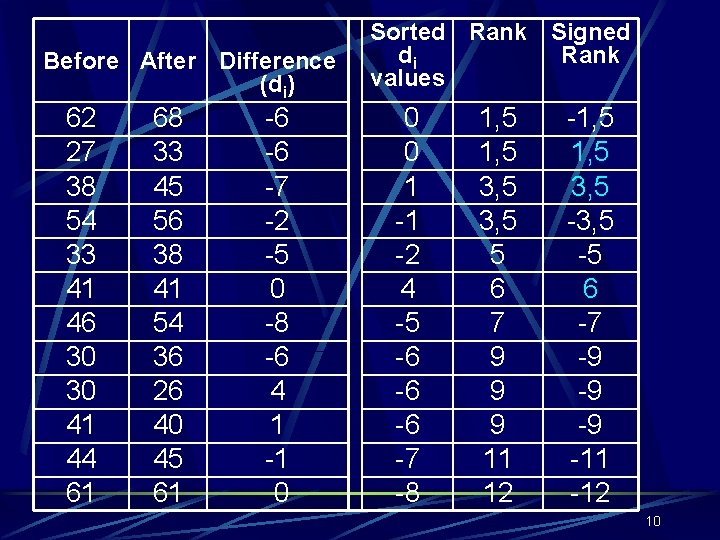
Before After Difference (di) 62 27 38 54 33 41 46 30 30 41 44 61 68 33 45 56 38 41 54 36 26 40 45 61 -6 -6 -7 -2 -5 0 -8 -6 4 1 -1 0 Sorted Rank Signed di Rank values 0 0 1 -1 -2 4 -5 -6 -6 -6 -7 -8 1, 5 3, 5 5 6 7 9 9 9 11 12 -1, 5 3, 5 -5 6 -7 -9 -9 -9 -11 -12 10

Assigning signes to ranks: For zero differences: • If there is one zero difference, exclude this observation from the analysis. • If the number of zero differences is even, assign plus signs to half of the ranks and minus signs to the other half. • If the number of zero differences is odd, exclude one observation from the analysis and follow the procuderes defined in the above step. For others: • Assign the sign of the difference to the rank. 11

Sum of negative ranks (T-)=62 Sum of positive ranks (T+)=11 T = 1, 5+3, 5+6=11 T =11 < Ttable = 14 , reject H 0, p<0. 05 12

The Significance Test for The Difference Between Two Dependent Population Proportions Instead of measurements, if number of subjects possessing a certain characteristic are recorded on two dependent samples, we test the hypothesis whether the two dependent proportions are equal or not. 13

After Before + - Total + a b a+b - c d c+d Total a+c b+d a+b+c+d=n p 1 = (a+b) / n OR n is large p 2 = (a+c) / n n is small 14

Example Two radiologists interpreted magnetic resonance images (MRI) of shoulders of 15 symptomatic patients. They independently evaluated the patients. The results of their evaluations are given in the table. Is there any significant difference between the propotions of positive evaluations of two radiologists? 15

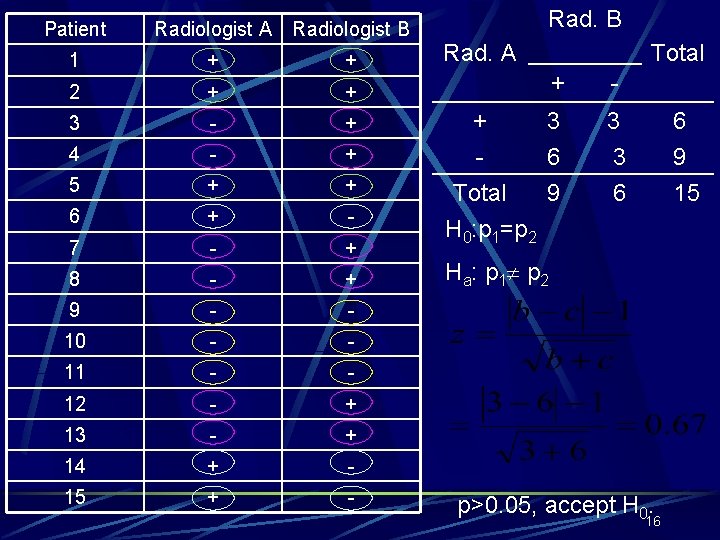
Patient Radiologist A Radiologist B 1 + + 2 + + 3 - + 4 - + 5 + + 6 + - 7 - + 8 - + 9 - - 10 - - 11 - - 12 - + 13 - + 14 + - 15 + - Rad. B Rad. A Total + - 3 3 6 6 9 Total H 0: p 1=p 2 3 6 9 15 + H a: p 1 p 2 p>0. 05, accept H 0. 16

Chi Square Test for paired Samples (Mc. Nemar Test) After Before + - Total + a b a+b - c d c+d Total a+c b+d a+b+c+d=n 17

Rad. B Rad. A Total + - + 3 3 6 - 6 3 9 Total 9 6 15 2(1, 0. 05)=3. 841>0. 444, p>0. 05; accept H 0. 18