Hyperon Star Model Ilona Bednarek Ustro 2009 Typical

Hyperon Star Model Ilona Bednarek Ustroń, 2009

Typical neutron star parameters: Neutron stars are the most compact objects • M ~ 1. 4 MS 1. 44 MS the largest precisely known neutron star mass • R ~ 10 km • g ~ 2 x 1014 cm s-2 • ~ 7 x 1014 g cm-3 (2 – 3) 0

Neutronof. Star Structure a neutron star • Atmosphere • Crust: – outer crust – from the atmosphere bottom to the density ND 4 x 1011 g cm-3 – inner crust – from ND to t (~ (0. 3 - 0. 5) x 0) – the inner edge separates the nonhomogenous crust from the homogenous liquid core, the transition density depends on the nuclear compression modulus and the density dependence of the nuclear symmetry energy • Core: – outer core - 0. 5 0 2 0 – neutrons, protons, electrons and muons – inner core - 2 0 does not occur in low mass stars whose outer core extends to the very center – hyperons

Minimal Model • Composition: - baryons - p, n, , +, -, 0 - mesons - , , , *, - leptons – e,

Vector Meson Potential softens the equation of state at higher density modifies the density dependence of the symmetry energy

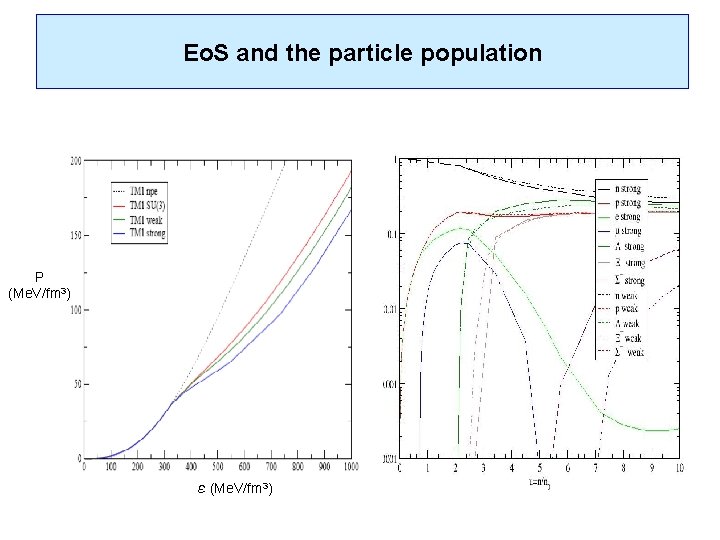
Eo. S and the particle population P (Me. V/fm 3)

Model with nonlinear vector meson interactions

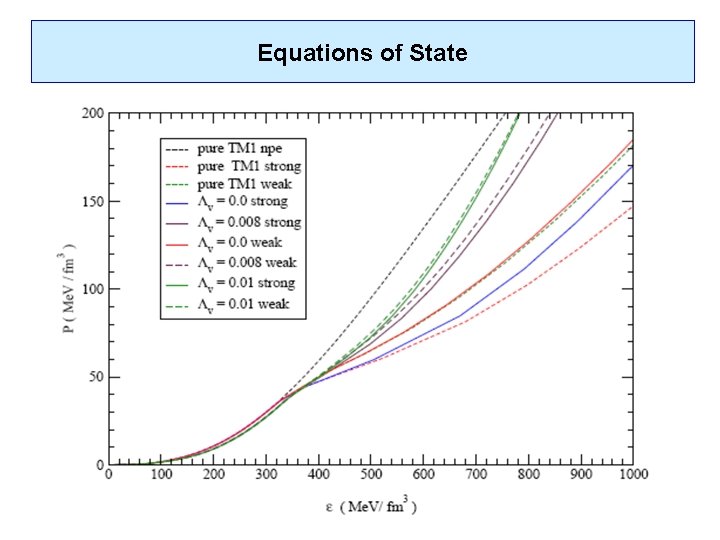
Equations of State

Additional nonlinear vector meson interactions modify: - density dependence of the Eo. S density dependence of the symmetry energy The energy per particle of nuclear matter The Eo. S around saturation density The values of L and Ksym govern the density dependence of sym around 0

Recent research in intermediate-energy heavy ion collisions is consistent with the following density dependence for < 0 Isospin diffusion ~ 0. 69 – 1. 05 Isoscaling data ~ 0. 69 The approximate formula for the core-crust transition density. (Prakash et al. 2007) Constraints from neutron skins - t ~ 0. 095 0. 01 fm-3 Results from microscopic Eo. S of Friedman and Pandharipande t ~ 0. 096 fm-3 does not support the direct URCA process

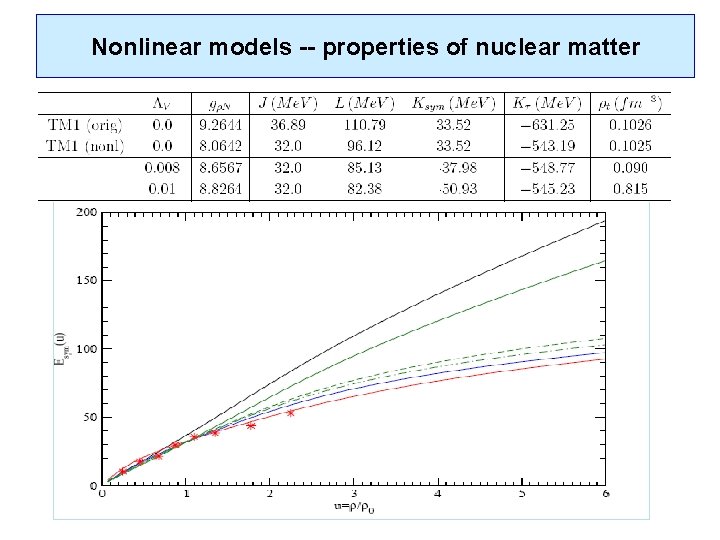
Properties models of nuclear for nononlinear Nonlinear -- matter properties of nuclear models matter

The Eo. S for the entire density span Outer crust – Baym-Pethick-Sutherland Eo. S of a cold nonaccreating neutron star (Baym et al. 1971) Inner crust – polytropic form of the Eo. S (Carriere et al. , 2003 ) out = 2. 46 x 10 -4 fm-3 the density separating the inner from the outer crust

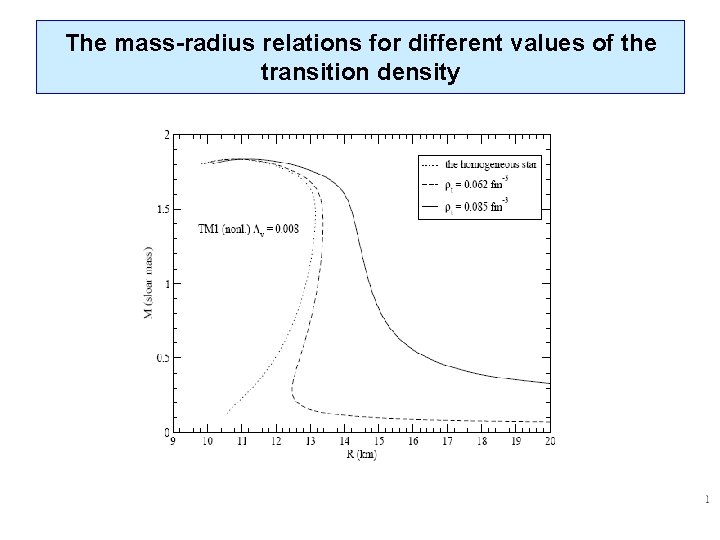
The mass-radius relations for different values of the transition density

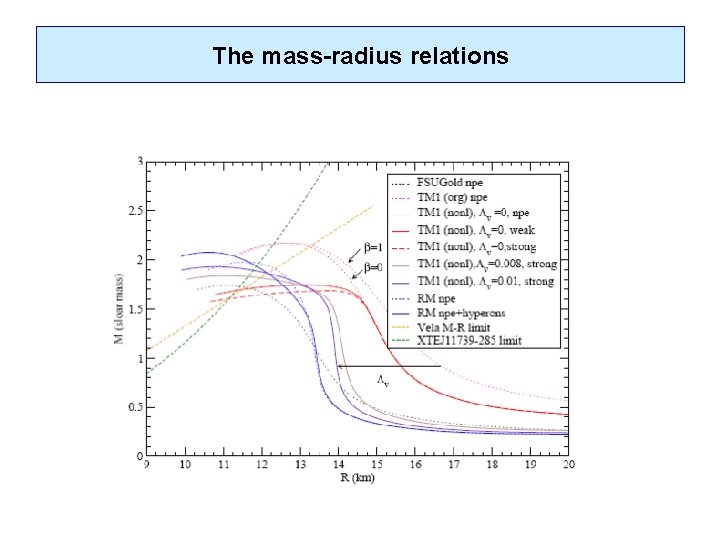
The mass-radius relations

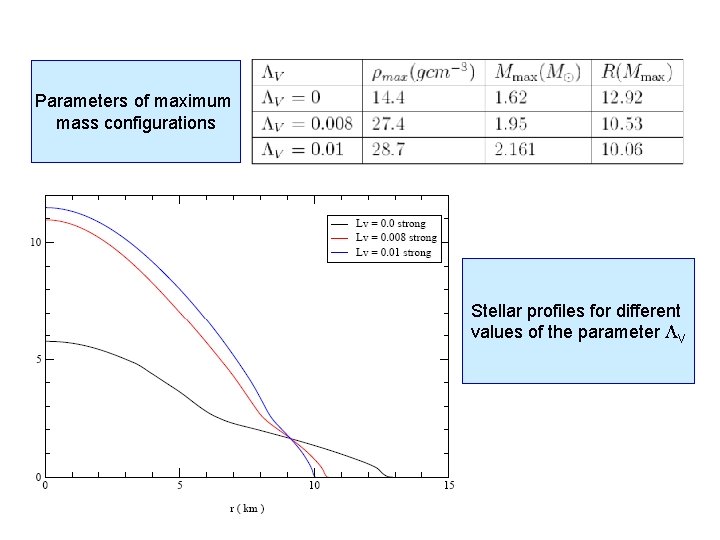
Parameters of maximum mass configurations Stellar profiles for different values of the parameter V

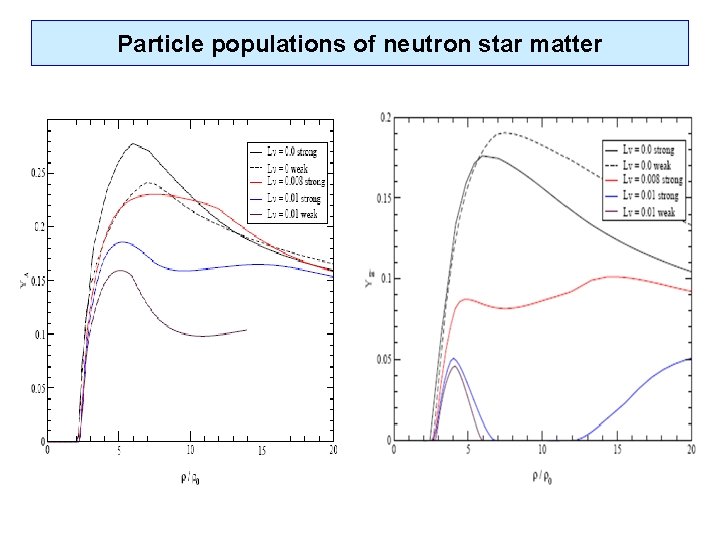
Particle populations of neutron star matter

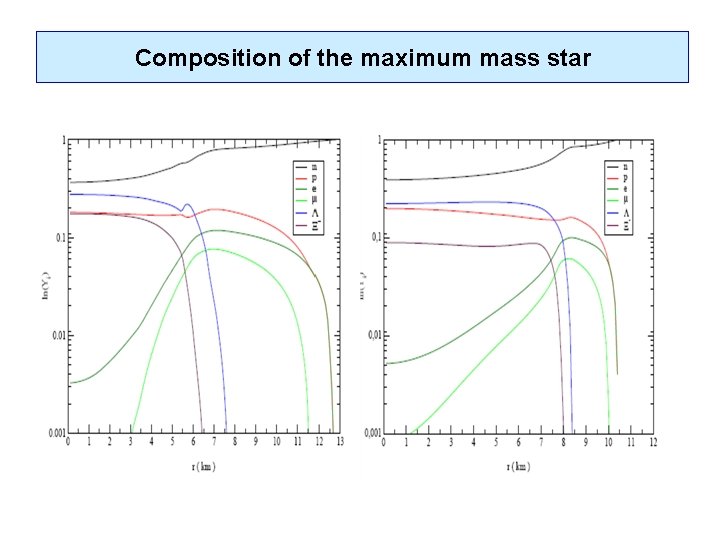
Composition of the maximum mass star

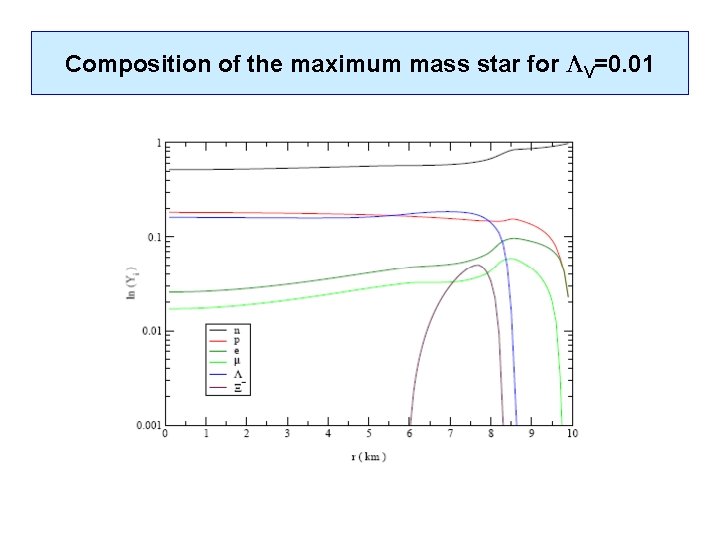
Composition of the maximum mass star for V=0. 01

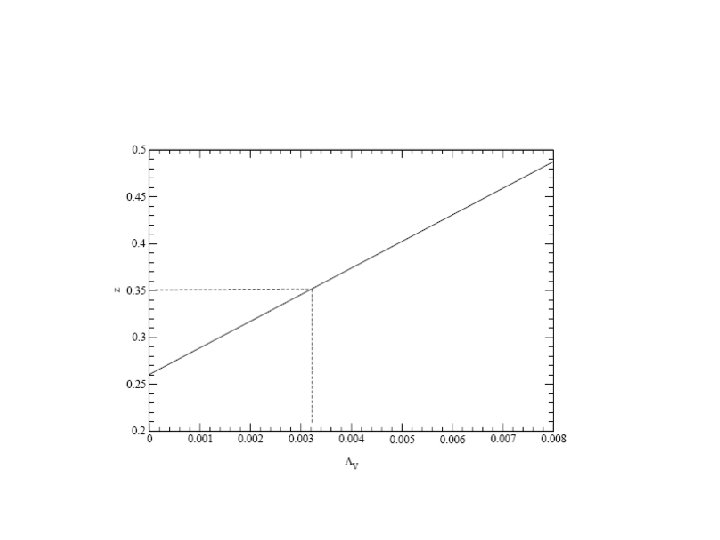
Astrophysical implications Location of the crust-core interface - crust thickness = R – Rt Moment of inertia connected with the crust The pressure at the boundary is very sensitive to the density dependence of the symmetry energy. 0. 20 Me. V fm-3 < Pt < 0. 65 Me. V fm-3 Using the upper limit of Pt the constraints for the minimum radius R for a given mass M for Vela can be obtained

Summary and Conclusion • Extended vector meson sector • Eo. S - considerably stiffer in the high density limit – higher value of the maximum mass • Modification of the density dependence of the symmetry energy • Transition density sensitive to the value of the parameter V • Modified structure of a neutron star