Hyperbelfunktionen Simone Kopp RuprechtKarlsUniversitt Heidelberg PS Analysis WS

Hyperbelfunktionen Simone Kopp Ruprecht-Karls-Universität Heidelberg PS Analysis, WS 08/09 Dozentin: PD Dr. Gudrun Thäter

Inhalt �Motivation �Hyperbelfunktionen �Zusammenhang �Umkehrfunktionen �Geometrische Definition

Bedeutung von Hyperbel �Griechisch: ὑπερβολή, hyperbolé die Übertreffung, Übertreibung, von altgriechisch hyperbállein übertreffen –

Anwendung �Spinnweben �Kettenlinie: ◦ Griechische Tempelsäulen ◦ Hochspannungsleitungen ◦ Stahlseile

Kettenlinie �Homogenes Seil hängt wegen Eigenlast durch und beschreibt eine Kosinus-Hyperbolicus Funktion �Kettenlinie = Seilkurve
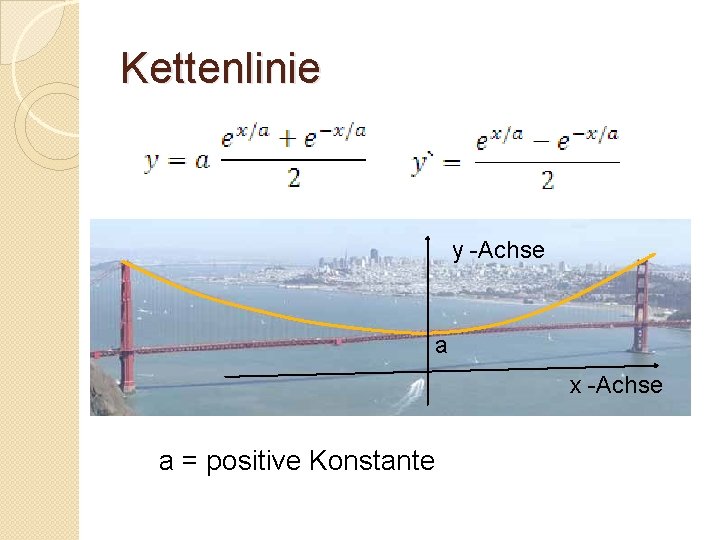
Kettenlinie y -Achse a x -Achse a = positive Konstante

Hyperbelfunktionen ◦ ◦ Kosinus Hyperbolicus (cosh) Sinus Hyperbolicus (sinh) Tangens Hyperbolicus (tanh) Cotangens Hyperbolicus (coth) ◦ Sekans Hyperbolicus (sech) ◦ Kosekans Hyperbolicus (csch)
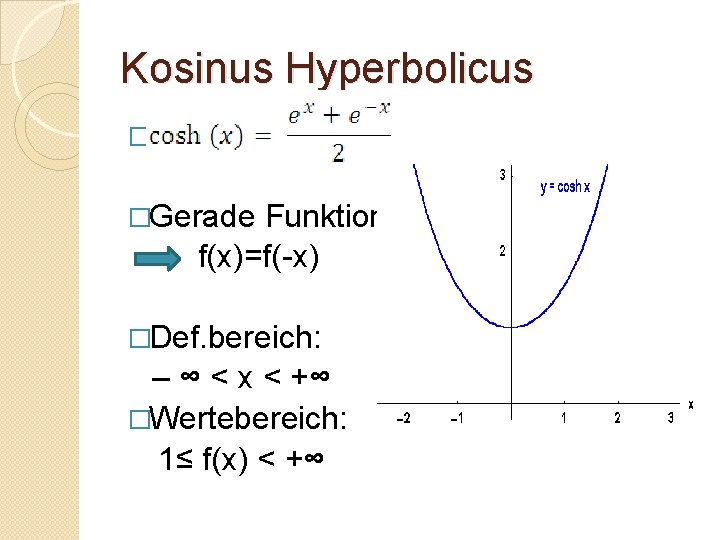
Kosinus Hyperbolicus � �Gerade Funktion f(x)=f(-x) �Def. bereich: – ∞ < x < +∞ �Wertebereich: 1≤ f(x) < +∞

Sinus Hyperbolicus � �Ungerade Funktion f(x)=-f(-x) �Def. bereich: – ∞ < x < +∞ �Wertebereich: – ∞ < f(x) < +∞
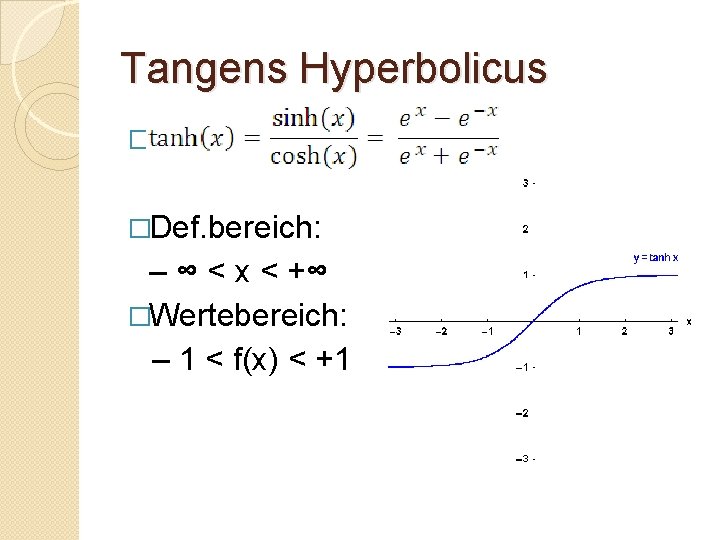
Tangens Hyperbolicus � �Def. bereich: – ∞ < x < +∞ �Wertebereich: – 1 < f(x) < +1

Cotangens Hyperbolicus � �Def. bereich: – ∞ < x < +∞ ; x ≠ 0 �Wertebereich: – ∞ < f(x) < – 1 ; 1 < f(x) < + ∞

Zusammenhang Additionstheoreme:

Zusammenhang �Differentiationsformeln: ◦ ◦

Zusammenhang �Viele Übereinstimmungen zu Sinus und Kosinus, usw Name: Sinus Hyperbolicus, Kosinus Hyperbolicus, usw

Umkehrfunktionen �werden Areafunktionen genannt (lat. area –Fläche) ◦ ◦ Area Kosinus Hyperbolicus (arcosh) Area Sinus Hyperbolicus (arsinh) Area Tangens Hyperbolicus (artanh) Area Cotangens Hyberbolicus (arcoth)
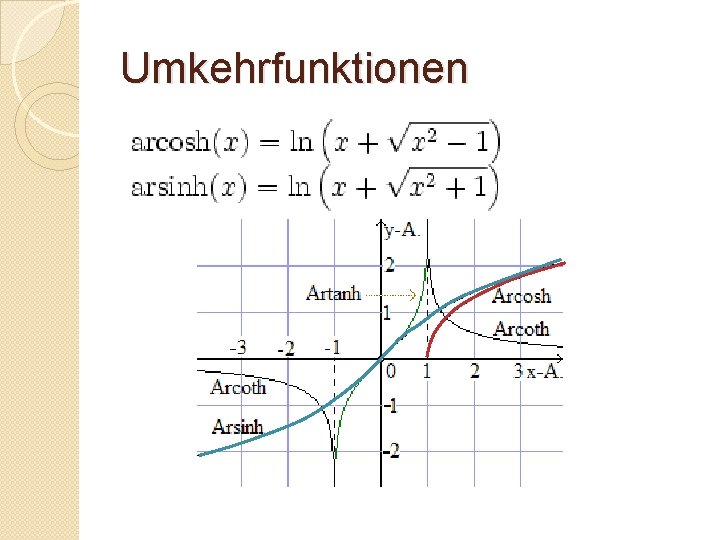
Umkehrfunktionen
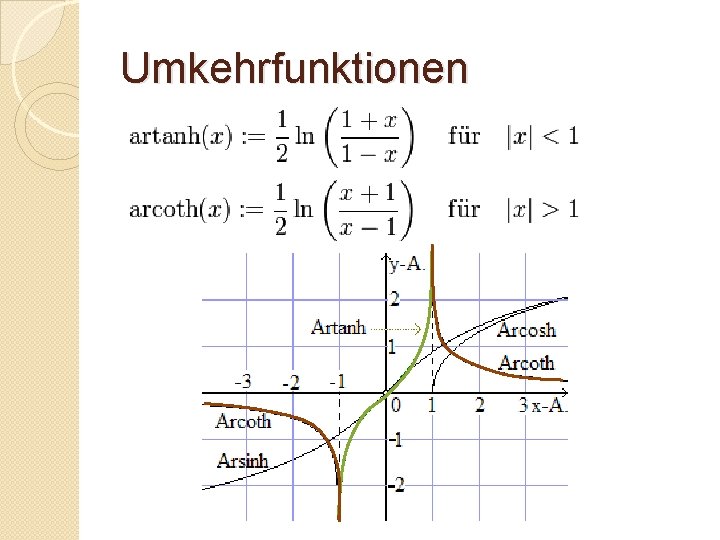
Umkehrfunktionen
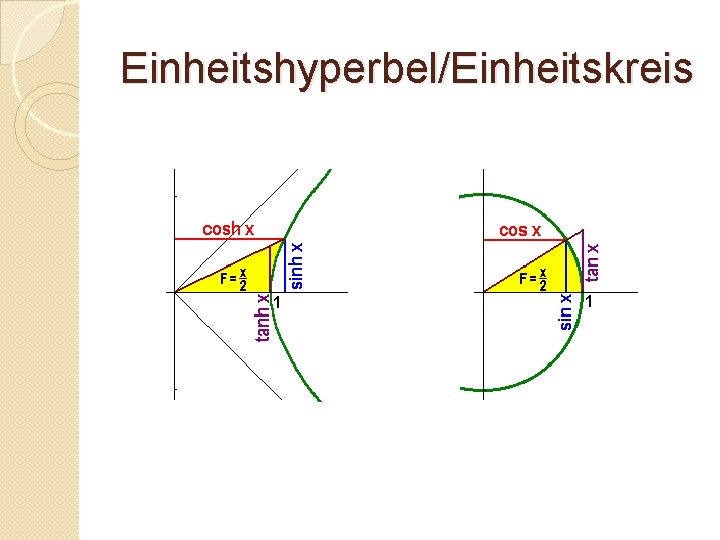
Einheitshyperbel/Einheitskreis
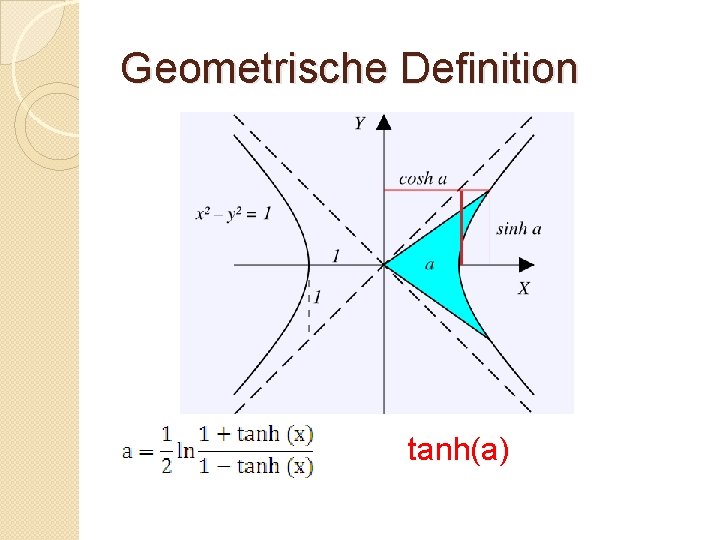
Geometrische Definition tanh(a)
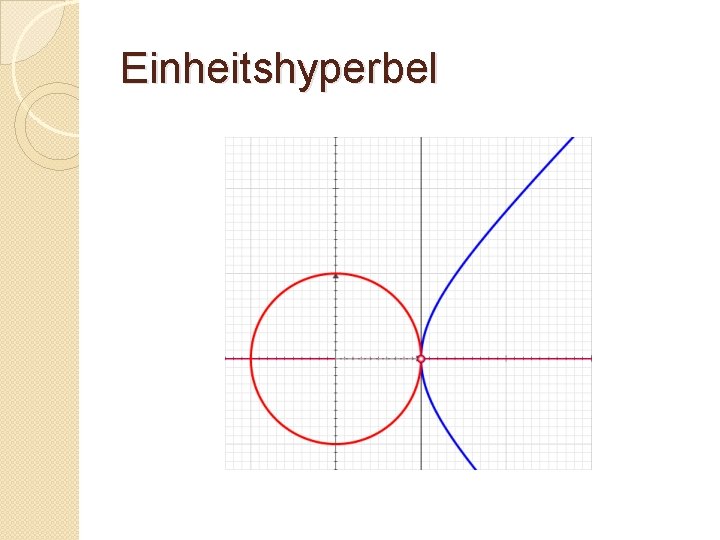
Einheitshyperbel
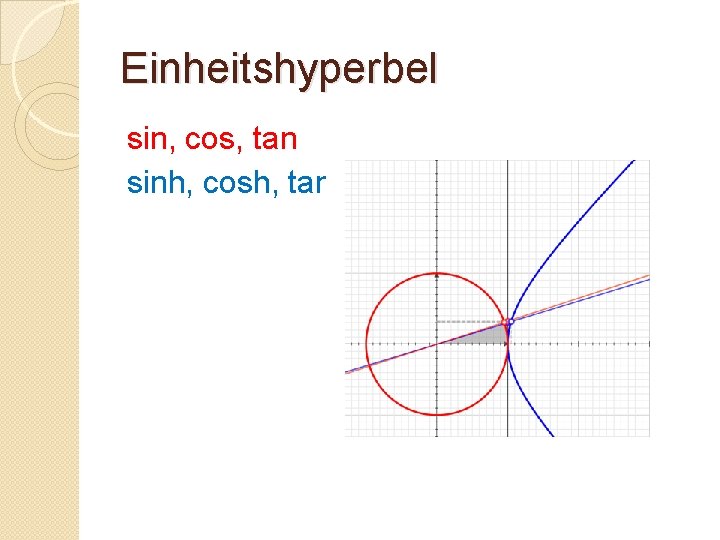
Einheitshyperbel sin, cos, tan sinh, cosh, tanh
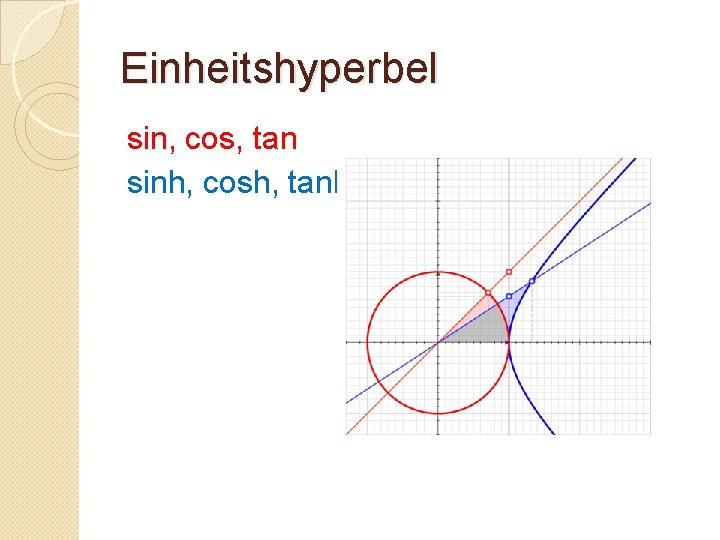
Einheitshyperbel sin, cos, tan sinh, cosh, tanh
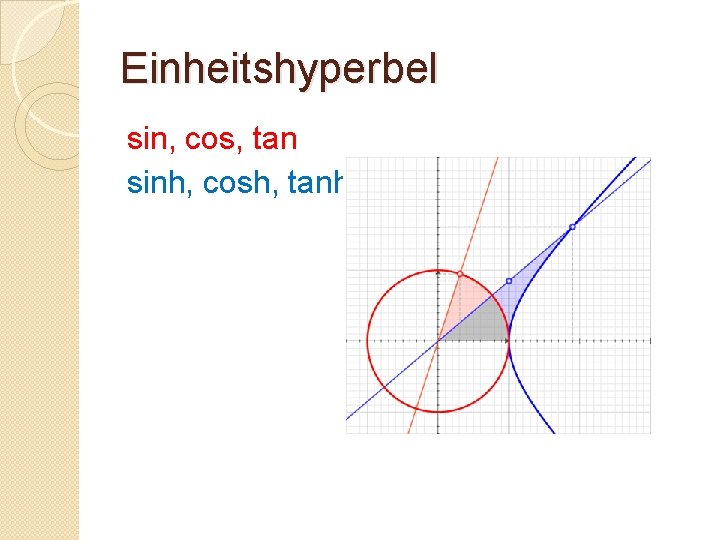
Einheitshyperbel sin, cos, tan sinh, cosh, tanh
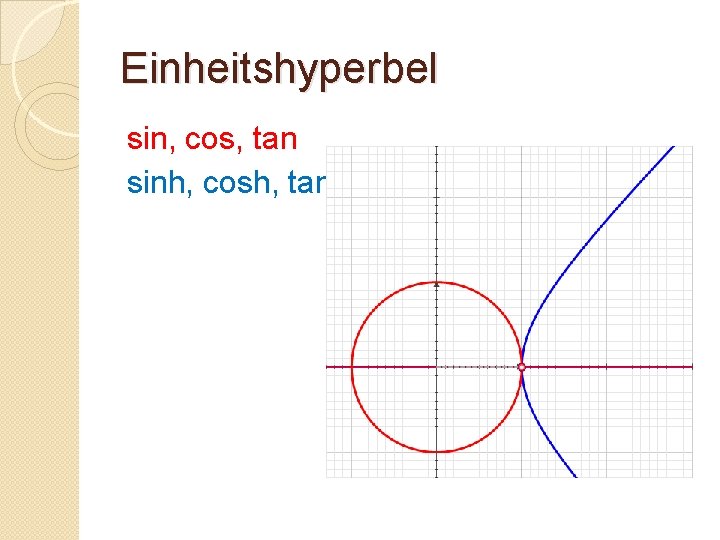
Einheitshyperbel sin, cos, tan sinh, cosh, tanh
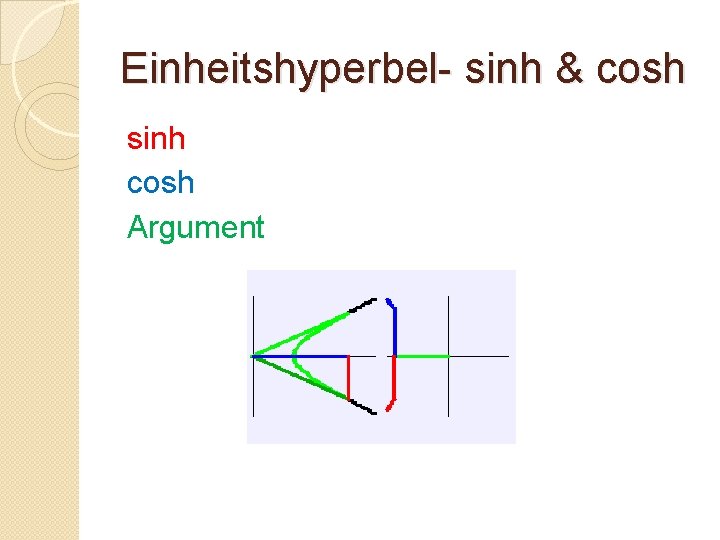
Einheitshyperbel- sinh & cosh sinh cosh Argument

Noch Fragen? ? ? Vielen Dank für Eure Aufmerksamkeit!
- Slides: 26