Hydrologie Literatura Hydrologie pro kombinovan studium Hydrologie Metodick

Hydrologie Literatura Hydrologie pro kombinované studium Hydrologie. Metodické návody do cvičení

Přednášky • • • Úvod, význam, základní pojmy Klimatičtí činitelé (srážky, vlhkost ovzduší, výpar) Geografičtí činitelé povodí Měření vodních stavů a průtoků Zpracování hydrologických dat Časové řady v hydrologii Režim vodních toků a extrémní průtoky Předpovědi vodních stavů a průtoků Podzemní vody Splaveniny

Cvičení • Geografičtí činitelé povodí • Vyhodnocení ombrogramu deště • Stanovení intenzity náhradního přívalového deště pro malé povodí • Stanovení průměrného srážkového úhrnu v provodí • Výpočet zásoby vody ve sněhové pokrývce • Vyhodnocení hydrometrování v měrném profilu na toku • Analýza reálné průtokové řady (4 cvičení) • Návrhový hydrogram povodně (Čerkašin, intenzitní vzorce) • Konstrukce hydrogramu povodně (jednotkový hydrogram)

Teoretické vědní obory - V • Hydor – voda • Logos – výskyt • Aulos - žlab • Hydor + logos • Hydor + aulos hydrologie hydraulika

Hydrologie Věda, která se systematicky a vlastními prostředky zabývá zákonitostmi výskytu a oběhu vody v přírodě Využití • Vodní stavby, hydrotechnika • Krajinné inženýrství • Zdravotní inženýrství • Dále stavebnictví a jiné rezorty

Vývoj hydrologie • Starověké civilizace • Do 15 stol. - intuice a dohady • Do 19. stol. – pozorování, měření, experimenty, modernizace, matematizace • Od r. 1900 jako samostatný vědní obor (Pitotova trubice, Chézyho rovnice, Hydrometrická vrtule

Styčné vědní obory • • Meteorologie a klimatologie Pedologie a geologie Agrotechnika Hydraulika Využívá vědní obory • Matematiku, teorii pravděpodobnosti a statistiku, fyziku, chemii a další

Dělení Hydrologie oceánů Hydrologie pevniny • Hydrometeorologie • Potamologie • Limnologie • Glaciologie • Hydropedologie

Složky hydrologie Hydrometrie Hydrografie • • Stochastická hydrologie Kinematická hydrologie ČHMÚ (Praha- Komořany, Brno, Ostrava, Hradec Králové, Ústí n/L, Plzeň, České Budějovice) Staniční síť Technologická linka (data režimová a operativní) Inženýrská hydrologie (data projektování a provoz)

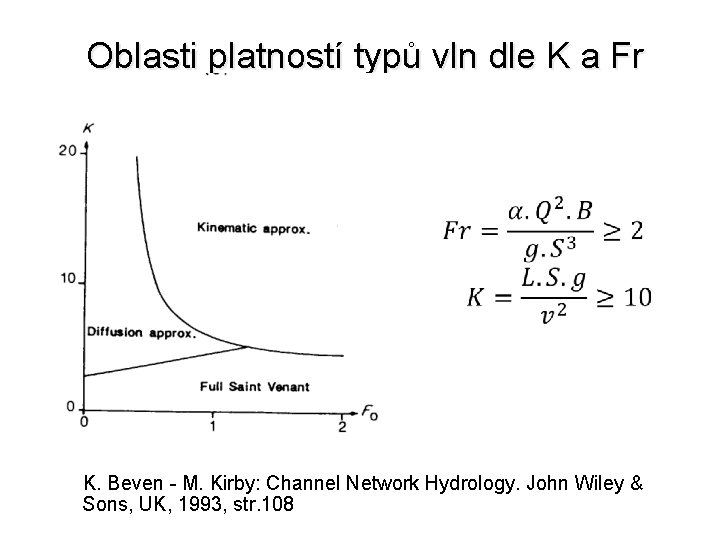
Oblasti platností typů vln dle K a Fr • K. Beven - M. Kirby: Channel Network Hydrology. John Wiley & Sons, UK, 1993, str. 108

Hydrosféra 70, 5 % zemského povrchu 1, 4. 109 km 3 – celkový objem vody 1, 3. 109 km 3 – moře a oceány 2, 4. 107 km 3 – ledovce 2, 3. 107 km 3 – podzemní voda 1, 3. 104 km 3 – atmosféra (0, 001%) 2, 1. 103 km 3 – vodní toky

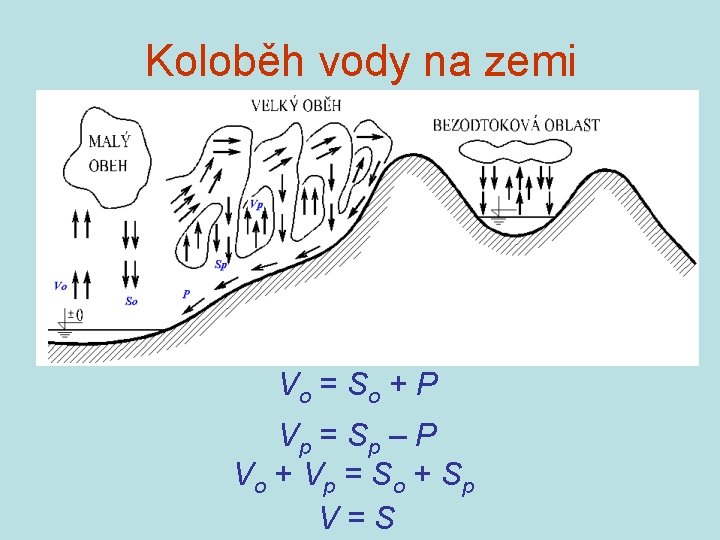
Koloběh vody na zemi Vo = So + P Vp = Sp – P Vo + Vp = So + Sp V=S

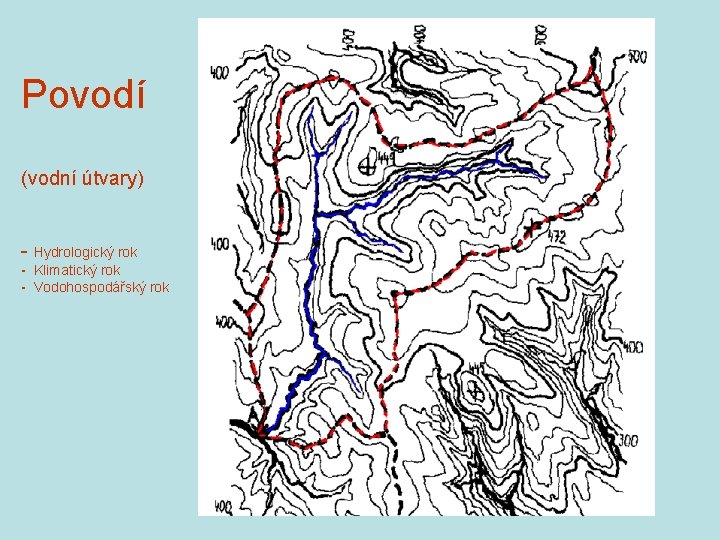
Povodí (vodní útvary) - Hydrologický rok - Klimatický rok - Vodohospodářský rok

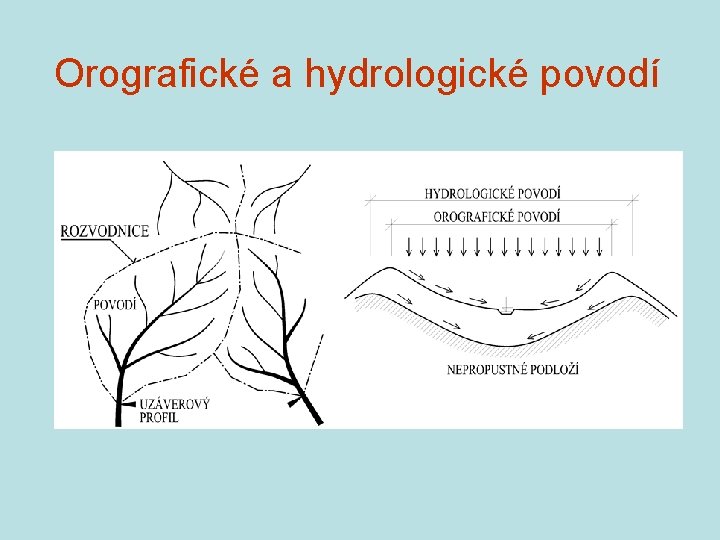
Orografické a hydrologické povodí

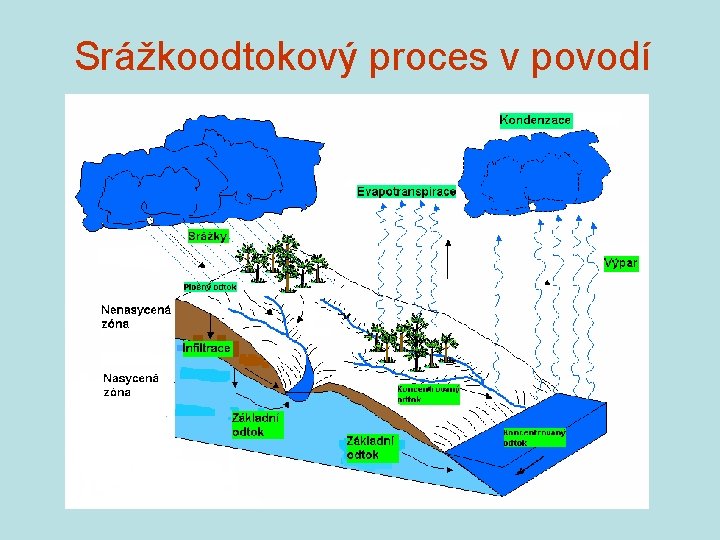
Srážkoodtokový proces v povodí

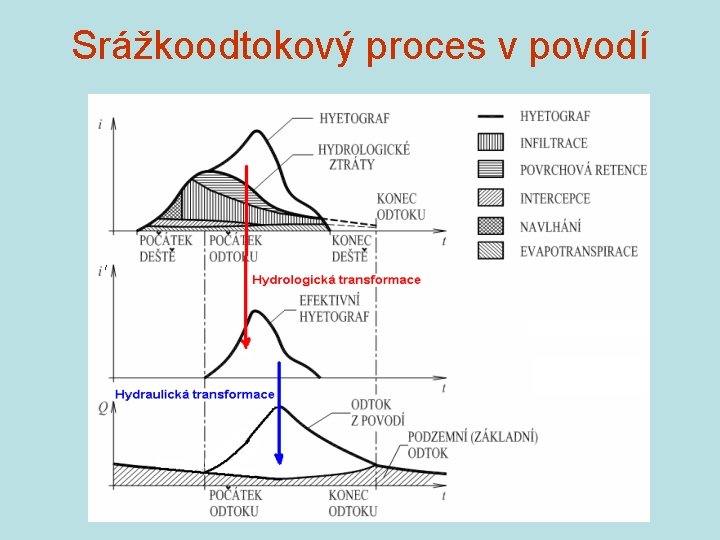
Srážkoodtokový proces v povodí

SOP - evoluční problém Počáteční podmínky – veličiny popisující stav vody v povodí v čase t = 0 Okrajové podmínky – stacionární (přítok vody z rozvodnice je nulový) – nestacionární (srážka nad povodím i(x, y, t))

Činitelé ovlivňující SOP Klimatičtí činitelé srážky, výpar, vlhkost ovzduší, teplota, tlak, vítr … Geografičtí činitelé fyzikálně geografičtí, geologické vlastnosti, vegetační pokryv, říční síť

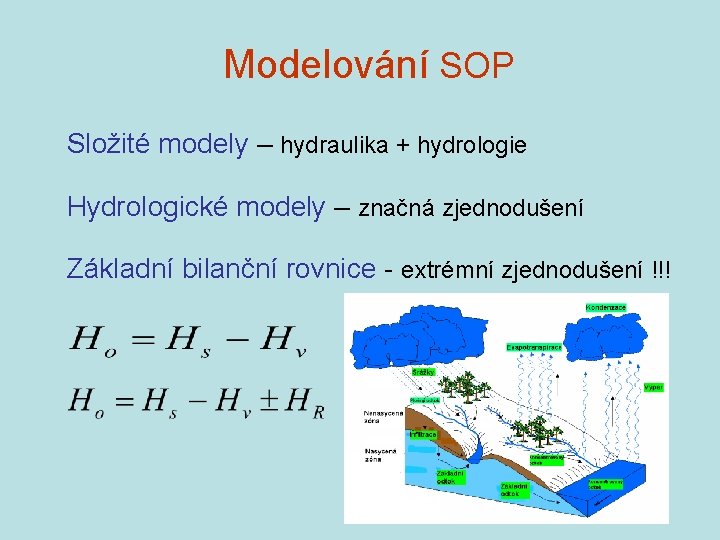
Modelování SOP Složité modely – hydraulika + hydrologie Hydrologické modely – značná zjednodušení Základní bilanční rovnice - extrémní zjednodušení !!!

Klimatičtí činitelé

Meteorologie a klimatologie Meteorologie • jevy probíhající v zemské atmosféře • momentální stav atmosféry • předpovědi počasí Klimatologie • nauka o podnebí • klasifikace podnebí a vymezování klimatických oblastí • studium kolísání a změn klimatu

Srážky Podle skupenství - kapalné, pevné Podle směru - vertikální, horizontální Popis: úhrn, intenzita, vydatnost • Pozorování srážek (staniční síť) - klimatické stanice (20 x 20 m, zatrav. , oploc. , ne mikroklima a vod. pl. ) základní (7 h, 14 h, 21 h + aut. reg. ), doplňkové (7 h) - srážkoměrné stanice • Homogenita měření (79 km 2 ) • Standardizace měření

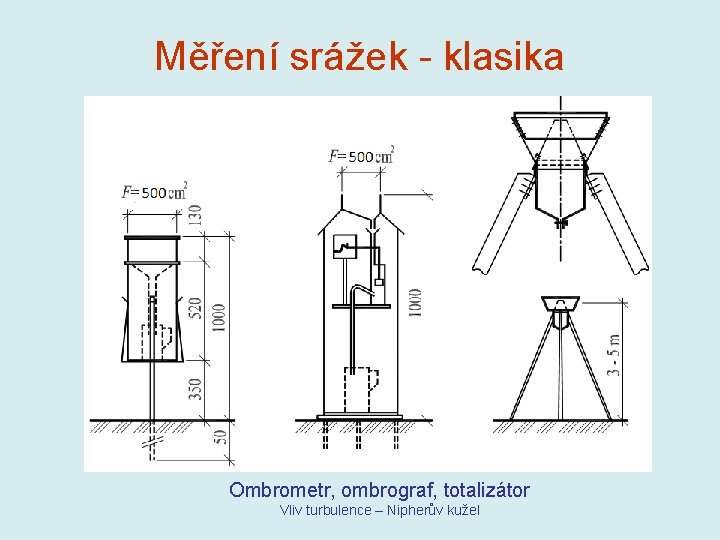
Měření srážek - klasika Ombrometr, ombrograf, totalizátor Vliv turbulence – Nipherův kužel

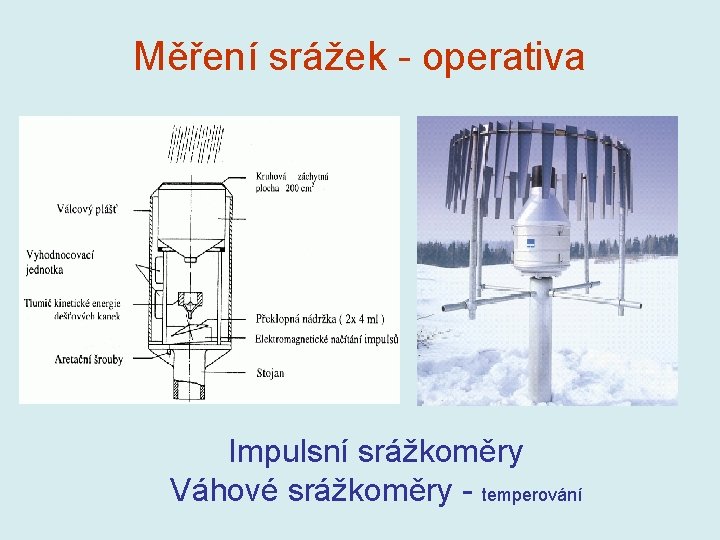
Měření srážek - operativa Impulsní srážkoměry Váhové srážkoměry - temperování

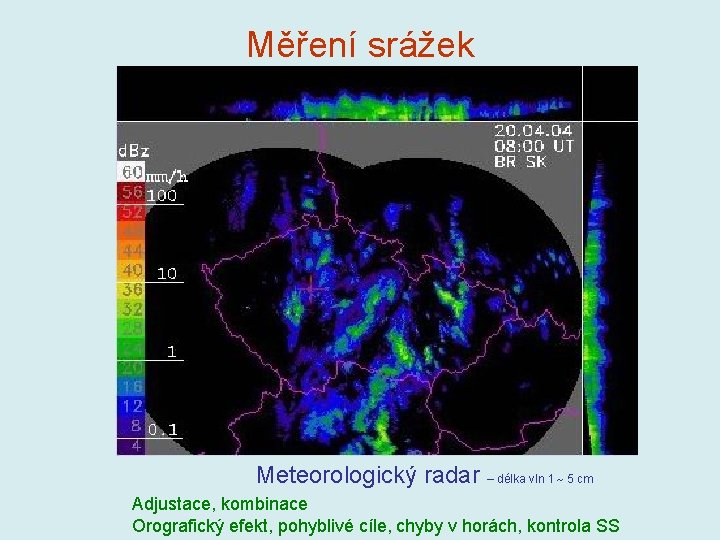
Měření srážek Meteorologický radar – délka vln 1 5 cm Adjustace, kombinace Orografický efekt, pohyblivé cíle, chyby v horách, kontrola SS

Měření srážek Meteorologická družice – METEOSAT, NOAH Polární, geostacionární – různé vlnové délky pro měření veličin

Předpovědi srážek Lace Orografie v ČR Aladin Délka předpovědí - nowcasting, forecasting

Srážky Plošné rozdělení srážek (úhrny za rok) ve světě: 2000 mm- rovník, 500 mm – tropy a subtropy (15 až 300), 500 -1000 mm mírný pás, 300 mm póly u nás: průměr 740 mm, 400 mm Žatecko, 1000 mm a více hory Časové rozdělení srážek roční chod: rovník- 2 max. 2 min (duben, říjen), subtropy- max. zima, min. léto, mírný- rovnom. u moře, vnitroz. max. léto, min. zima u nás (25%, 40%, 20%, 15% - J, L, P, Z) denní chod (mírný pás): pobřeží- max. den, min. noc, pevnina- 2 max. a 2 min. Metody stanovení průměrných Hs v povodí aritmetický průměr Hortonova (Thiessenova) polygonální metoda hyetografická křivka Prověření homogenity Hs Podvojná součtová čára

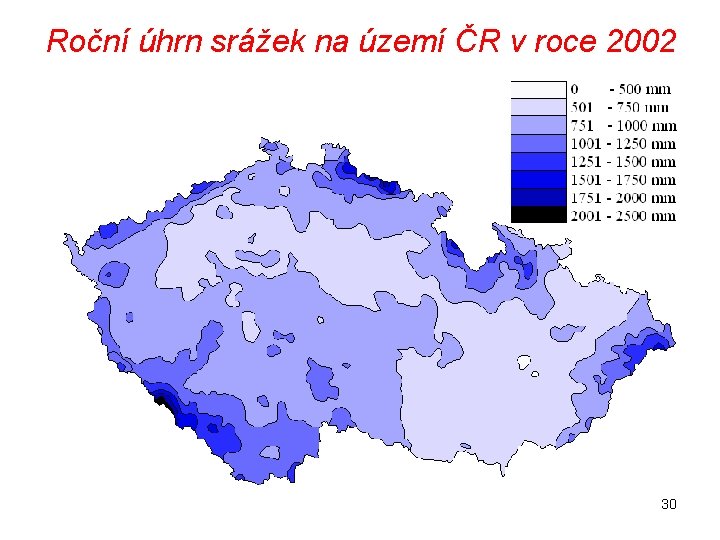
Roční úhrn srážek na území ČR v roce 2002 30

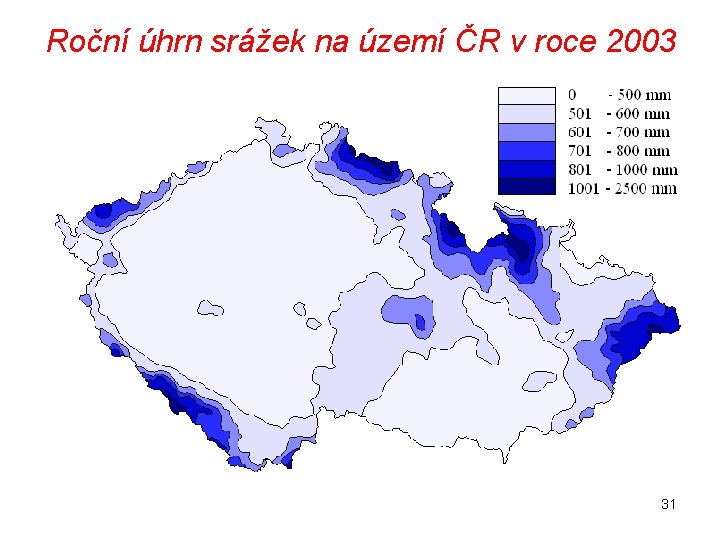
Roční úhrn srážek na území ČR v roce 2003 31

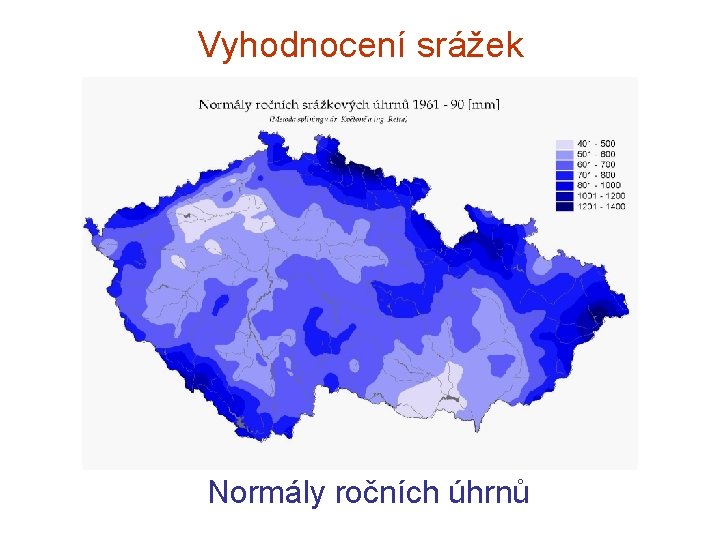
Vyhodnocení srážek Normály ročních úhrnů

Deště Srážky - kapalné, vertikální •

Deště Ombrogram, čára náhradních intenzit (cvič. ) Intenzita [mm. h-1] Periodicita Průměrná doba opakování [počet roků]

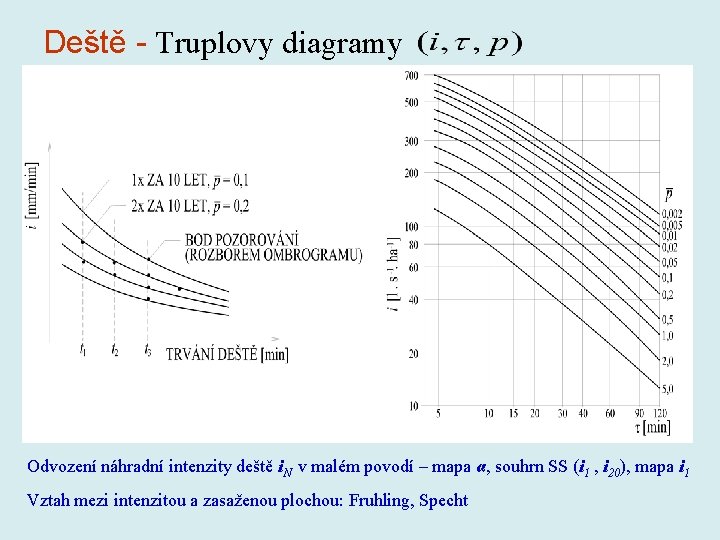
Deště - Truplovy diagramy Odvození náhradní intenzity deště i. N v malém povodí – mapa α, souhrn SS (i 1 , i 20), mapa i 1 Vztah mezi intenzitou a zasaženou plochou: Fruhling, Specht

Sněhová pokrývka Vodní hodnota - HV Specifická vodní hodnota Objemová hmotnost Tání sněhové pokrývky Metoda stupeň-den

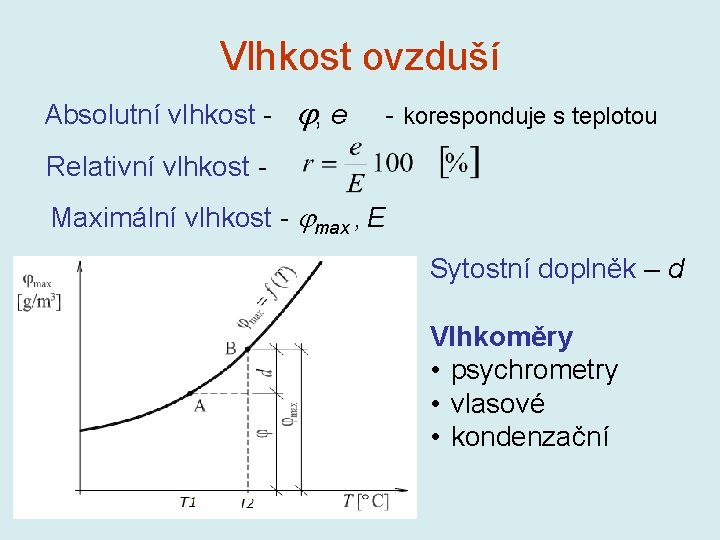
Vlhkost ovzduší Absolutní vlhkost - , e - koresponduje s teplotou Relativní vlhkost Maximální vlhkost - max , E Sytostní doplněk – d Vlhkoměry • psychrometry • vlasové • kondenzační

Výpar •

Výpar z vodní hladiny V průměru 1 – 4 mm za den V průměru 480 – 800 mm za rok Kdy nastává: Tvo X Tvz Co ovlivňuje velikost výparu: teplota vody a vzduchu, tlak v ovzduší, proudění vzduchu, vlhkost vzduchu, kvalita vody, zakřivení povrchu Stanovení velikosti výparu: metody nepřímé a přímé

Stanovení výparu z vodní hladiny – metody nepřímé měs XI XII IV V VI VIII IX X k % 5 2 1 2 6 9 12 14 16 15 11 7

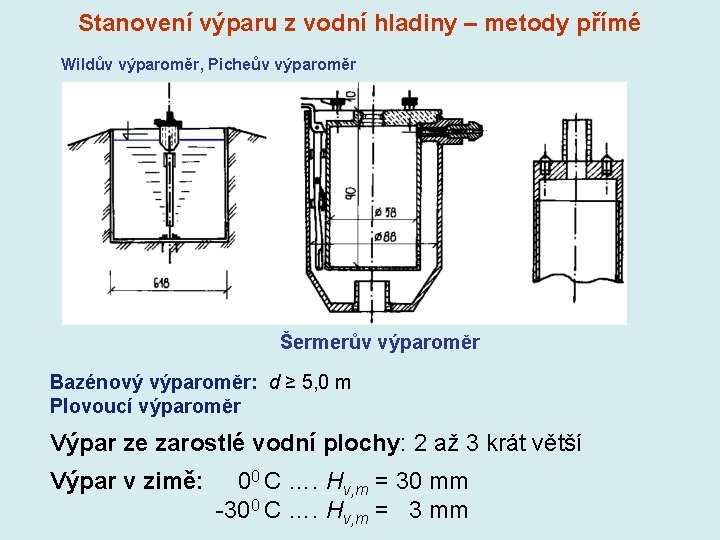
Stanovení výparu z vodní hladiny – metody přímé Wildův výparoměr, Picheův výparoměr Šermerův výparoměr Bazénový výparoměr: d ≥ 5, 0 m Plovoucí výparoměr Výpar ze zarostlé vodní plochy: 2 až 3 krát větší Výpar v zimě: 00 C …. Hv, m = 30 mm -300 C …. Hv, m = 3 mm

Výpar z půdy Holé půdy Hladina podzemní vody v úrovni terénu HV, p = 1, 0. HV, v - lehké písčité hlíny HV, p = 0, 9. HV, v - hlíny HV, p = 0, 8. HV, v - jíly Snížená hladina podzemní vody HV, p = 400 mm/rok - těžké hlíny HV, p = 200 mm/rok - písčité hlíny Půdy porostlé vegetací Transpirace – ovlivňují vnější a vnitřní faktory Transpirační koeficient - 200 až 900 litrů vody Měření transpirace – phytometr, potometr

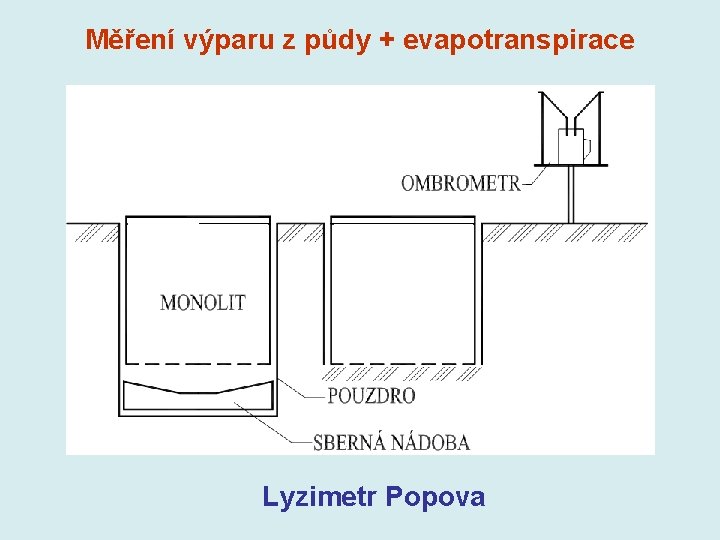
Měření výparu z půdy + evapotranspirace Lyzimetr Popova

Geografičtí činitelé

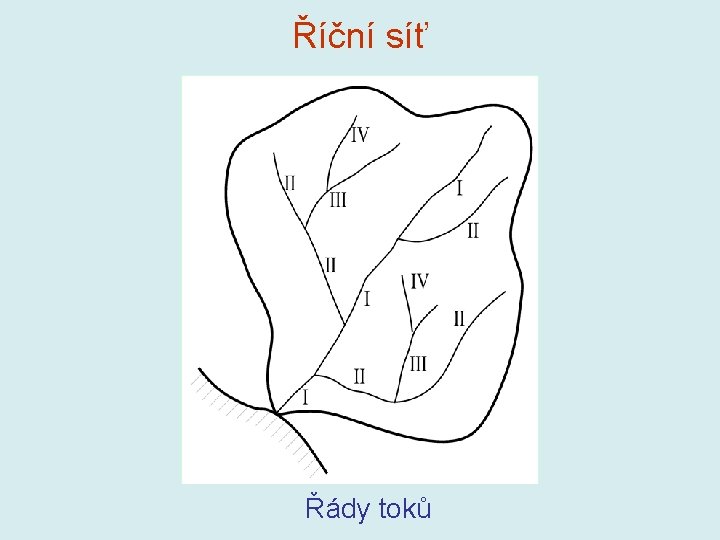
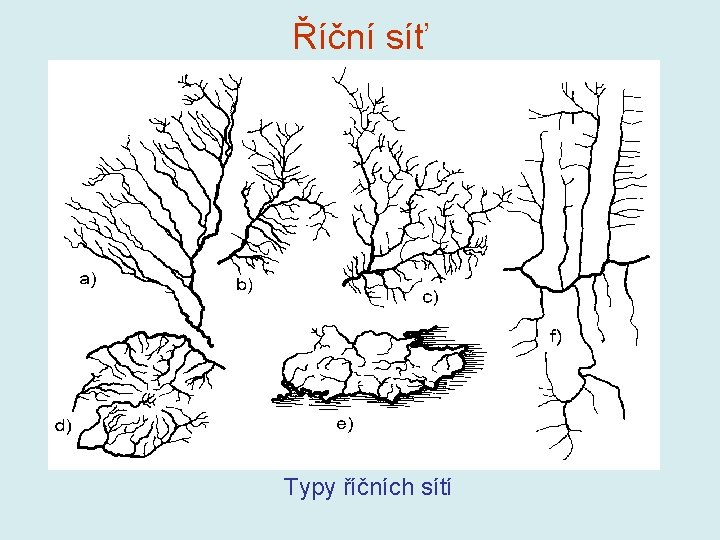
Geografičtí činitelé povodí • Fyzikálně geometrické vlastnosti (poloha, velikost, tvar, sklonitost) • Geologické vlastnosti (drsnost, rychlost vsaku, proudění v nenasycené a nasycené zóně) • Vegetační pokryv (rychlost povrchového odtoku, infiltrace) • Říční síť (rychlost odtoku vody z povodí)

Fyzikálně geometrické vlastnosti povodí

Geologické vlastnosti povodí

Vegetační pokryv

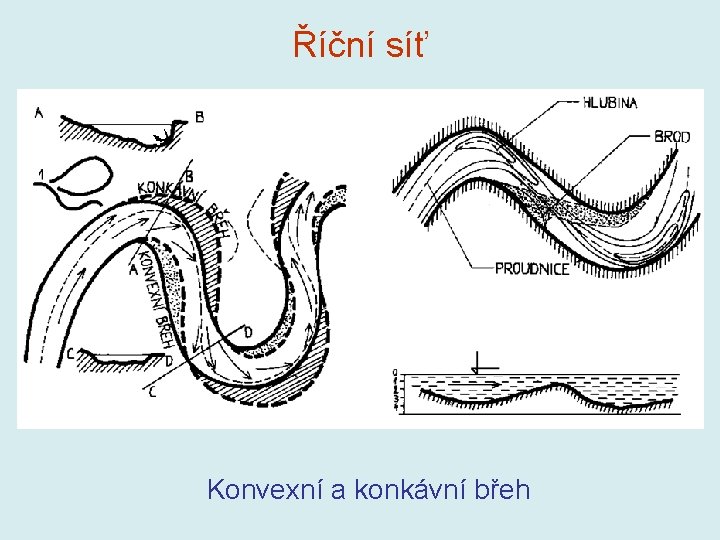
Říční síť Konvexní a konkávní břeh

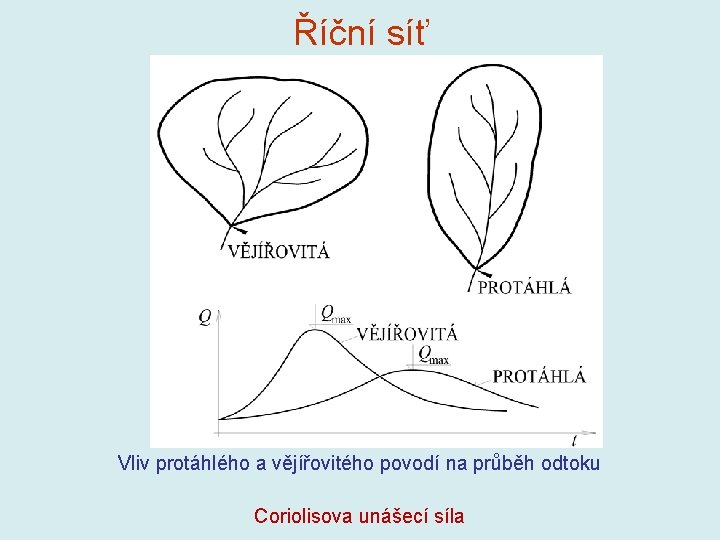
Říční síť Vliv protáhlého a vějířovitého povodí na průběh odtoku Coriolisova unášecí síla

Měření vodních stavů a průtoků 54

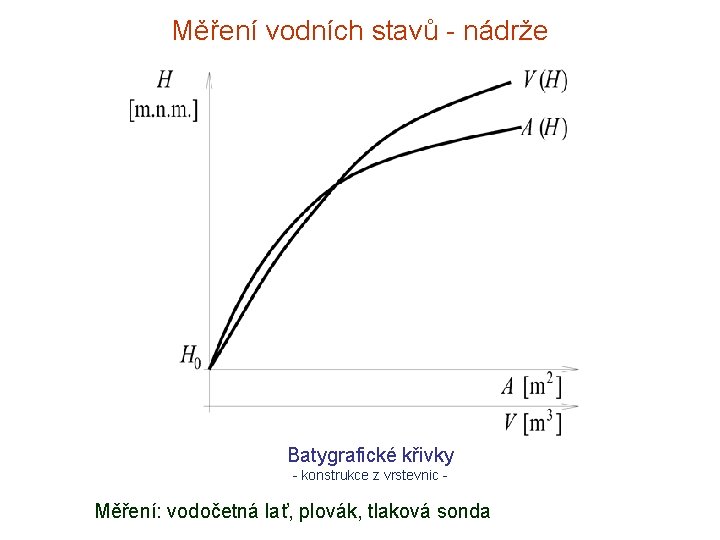
Měření vodních stavů - nádrže Batygrafické křivky - konstrukce z vrstevnic - Měření: vodočetná lať, plovák, tlaková sonda

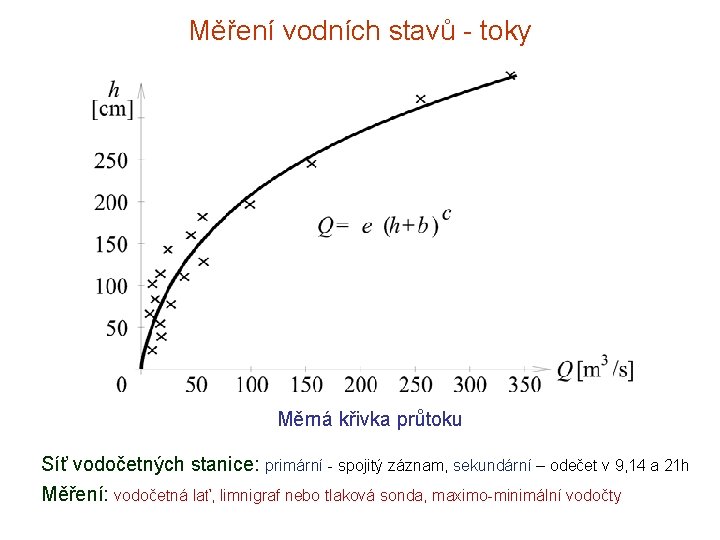
Měření vodních stavů - toky Měrná křivka průtoku Síť vodočetných stanice: primární - spojitý záznam, sekundární – odečet v 9, 14 a 21 h Měření: vodočetná lať, limnigraf nebo tlaková sonda, maximo-minimální vodočty

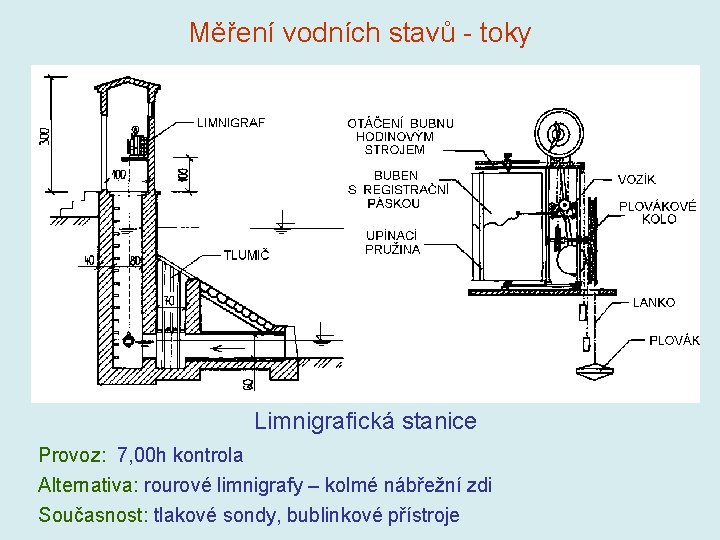
Měření vodních stavů - toky Limnigrafická stanice Provoz: 7, 00 h kontrola Alternativa: rourové limnigrafy – kolmé nábřežní zdi Současnost: tlakové sondy, bublinkové přístroje

Měření vodních stavů - toky Kritéria pro výběr měrných profilů • Přístupnost • Přímý úsek toku • Vhodnost pro hydrometrování • Ne vliv vzdutí nebo snížení • Veškerý průtok měrným profilem 58

Měření průtoků – vodní toky

Měření průtoků – vodní toky

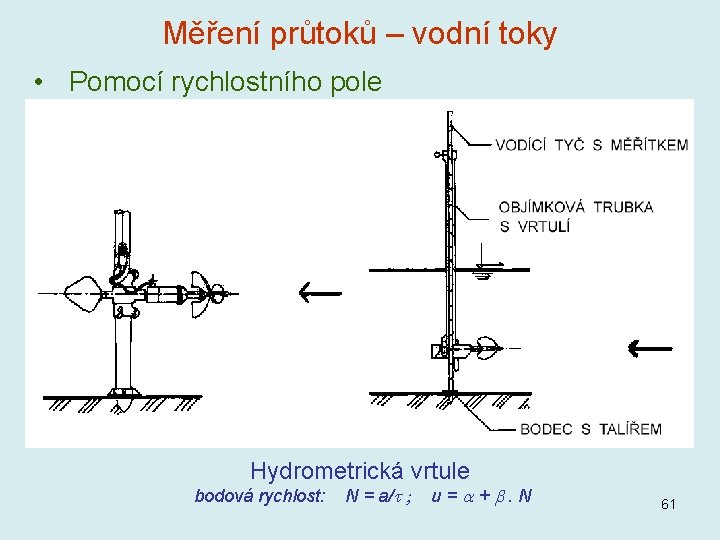
Měření průtoků – vodní toky • Pomocí rychlostního pole Hydrometrická vrtule bodová rychlost: N = a/ u= +. N 61

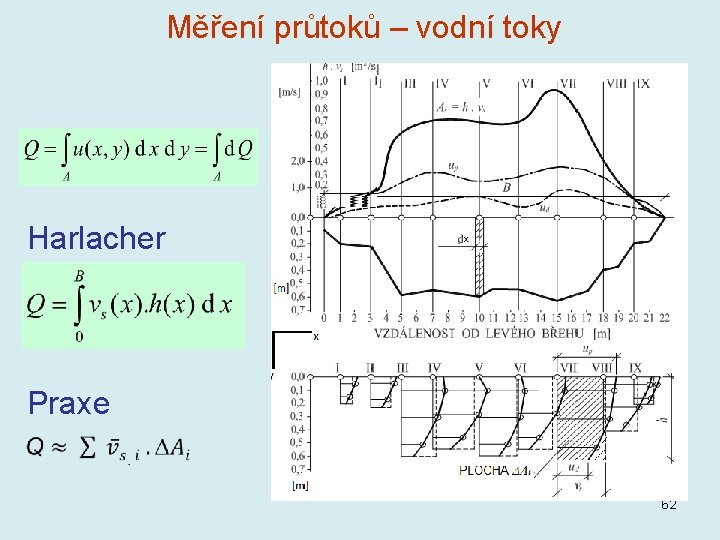
Měření průtoků – vodní toky Harlacher Praxe 62

Měření průtoků – vodní toky Určení vs • Bodové metody 1 bod: vs u 0, 6 h 2 body: vs (u 0, 2 h + u 0, 8 h)/2 3 body: vs (u 0, 2 h + 2. u 0, 6 h + u 0, 8 h)/4 • Aproximace optimalizovanými kubickými spliny (HYDROS) Harlacher – numerická integrace Rychlostní pole – numerická integrace 63

Měření průtoků – vodní toky • Početně grafická metoda vyhodnocení hydrometrování • Indukční sondy místo hydrometrické vrtule • Měření ultrazvukem (Stork, Quantum, Ott) • Měřící systém ADCP (Acoustic Doppler Current Profiler) 64

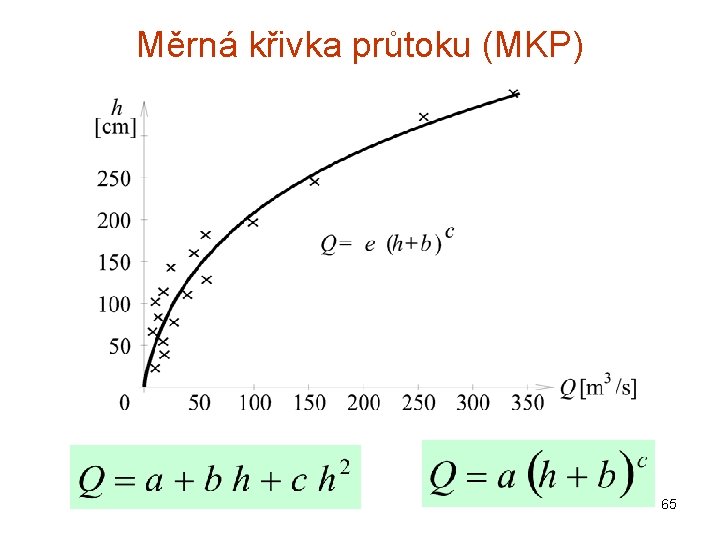
Měrná křivka průtoku (MKP) 65

Měrná křivka průtoku (MKP) • Lomový bod • Vymílání zanášení koryta toku • Vegetační nevegetační období • Málo bodů v horní části MKP • Hystereze MKP 66

Zpracování hydrologických dat 67

Zpracování hydrologických dat Náhodný jev • Náhodná veličina X: • Náhodný proces X(t): x 1, x 2, ……. . , xn x 1(t), x 2(t), ……. . , xn(t) Základní soubor Náhodný výběr 68

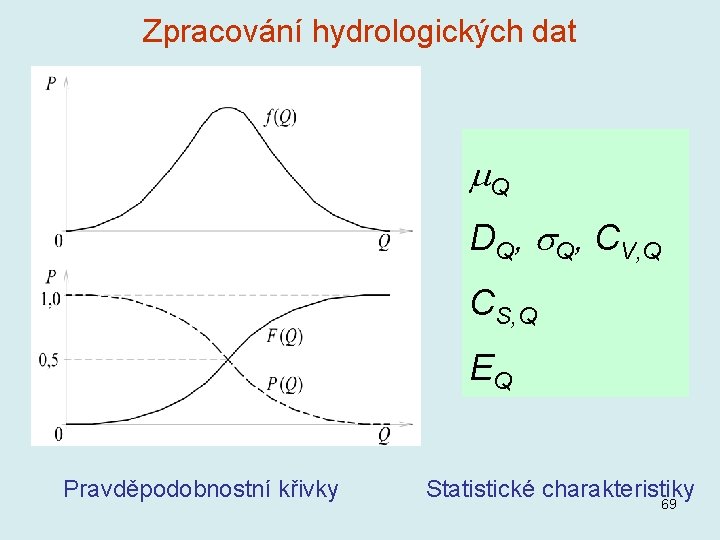
Zpracování hydrologických dat Q DQ, Q, CV, Q CS, Q EQ Pravděpodobnostní křivky Statistické charakteristiky 69

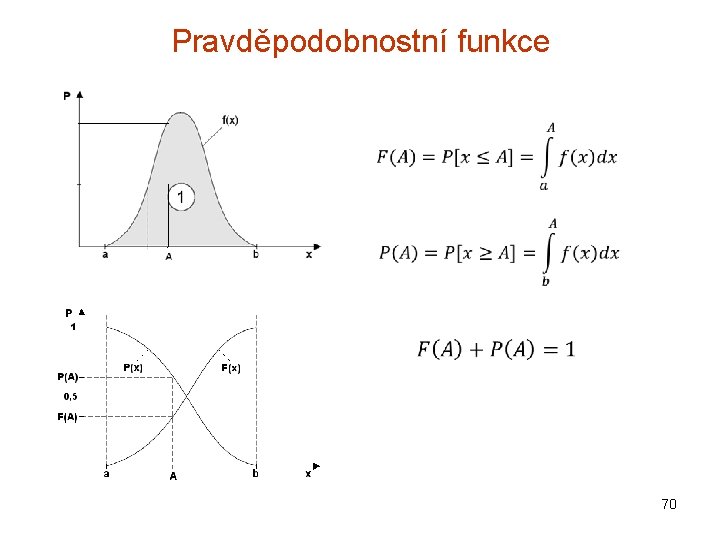
Pravděpodobnostní funkce 70

Statistické charakteristiky - metoda momentů 71

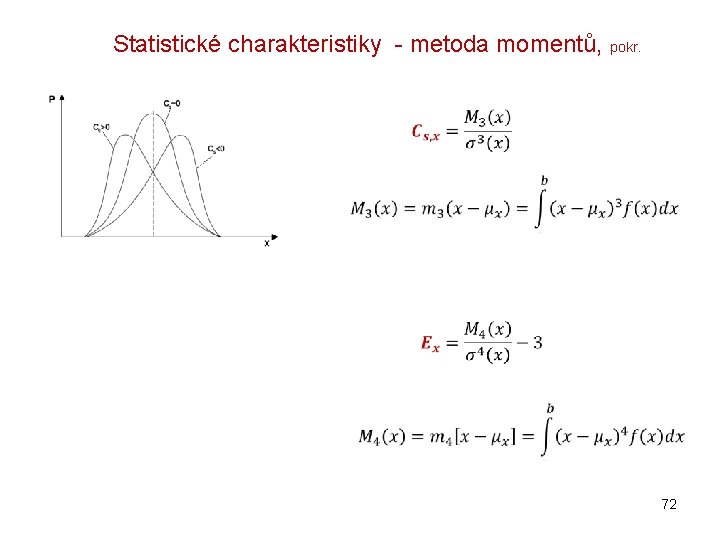
Statistické charakteristiky - metoda momentů, pokr. 72

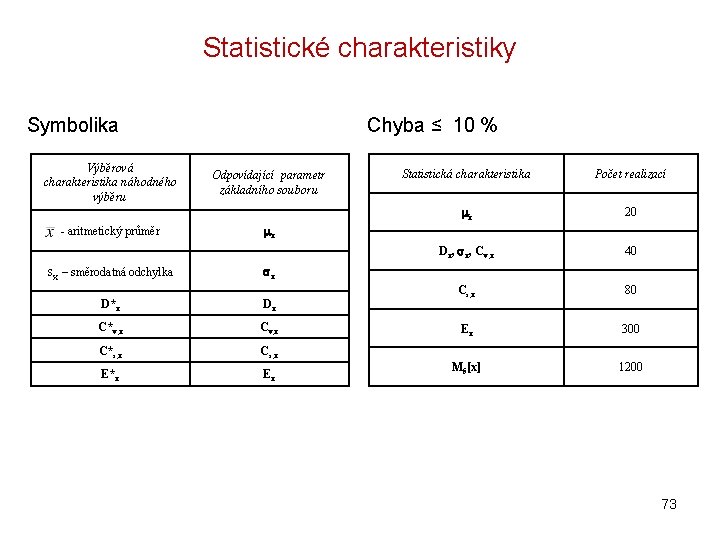
Statistické charakteristiky Symbolika Výběrová charakteristika náhodného výběru - aritmetický průměr Chyba ≤ 10 % Odpovídající parametr základního souboru Statistická charakteristika Počet realizací x 20 Dx, x, Cv, x 40 Cs, x 80 Ex 300 M 5[x] 1200 x sx – směrodatná odchylka x D*x Dx C*v, x C*s, x Cs, x E*x Ex 73

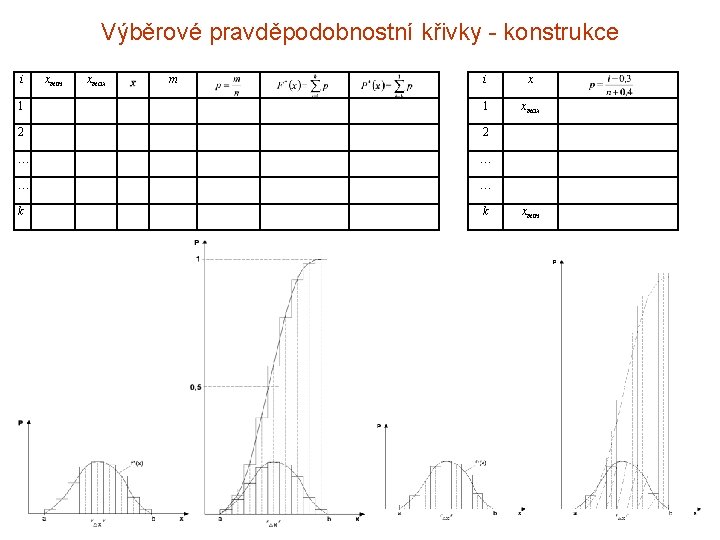
Výběrové pravděpodobnostní křivky - konstrukce i xmin xmax m i x 1 1 xmax 2 2 … … k k xmin 74

Výběrové charakteristiky - metoda momentů

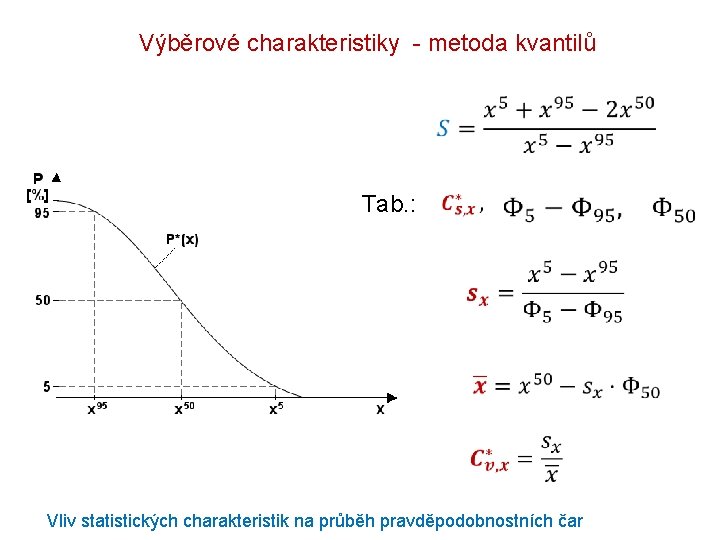
Výběrové charakteristiky - metoda kvantilů Tab. : Vliv statistických charakteristik na průběh pravděpodobnostních čar

Aproximace empirických rozdělení pravděpodobnosti teoretickými Měřená hydrologická data problémy při proložení empirických pravděpodobnostních čar: • ve střední části mnoho bodů, • na koncích velmi málo bodů. Problematický odečet extrémních hodnot hydrologických údajů !!! Aproximace pravděpodobnostních křivek funkcí: • ve střední části vyhlazení, na koncích extrapolace, • objektivizace proložení.

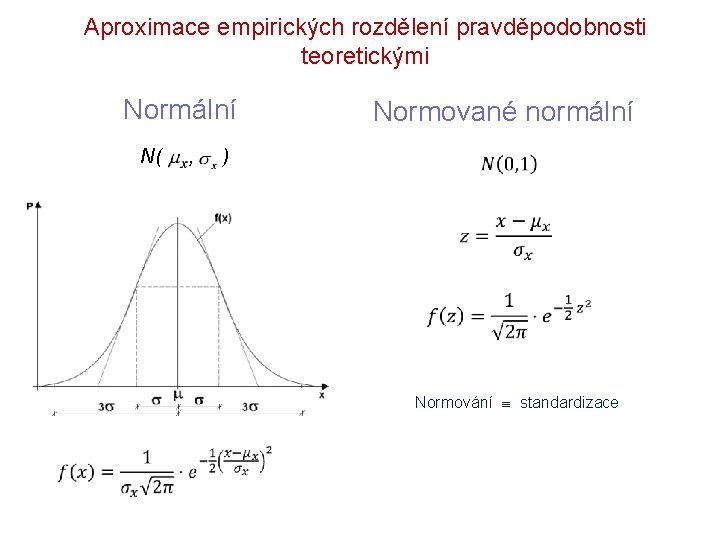
Aproximace empirických rozdělení pravděpodobnosti teoretickými Normální N( , Normované normální ) Normování standardizace

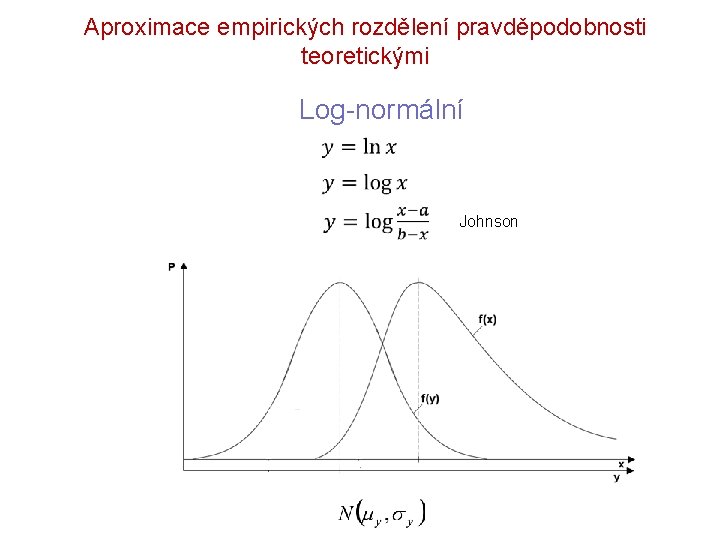
Aproximace empirických rozdělení pravděpodobnosti teoretickými Log-normální Johnson

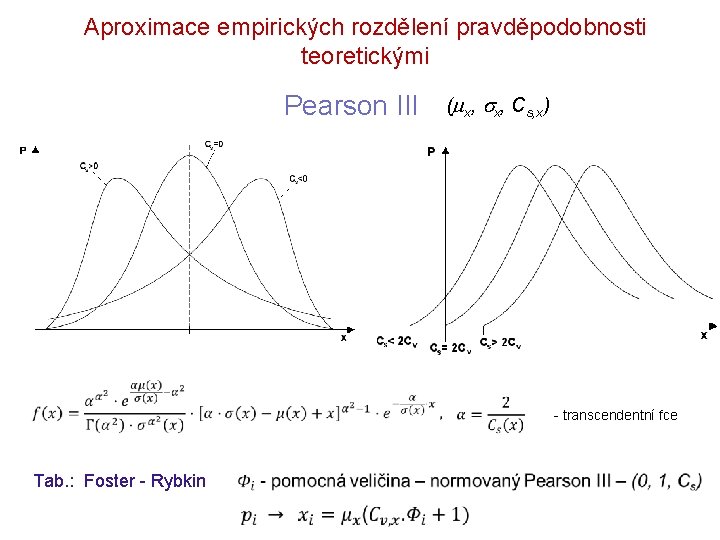
Aproximace empirických rozdělení pravděpodobnosti teoretickými Pearson III ( x, Cs, x) - transcendentní fce Tab. : Foster - Rybkin

Aproximace empirických rozdělení pravděpodobnosti teoretickými Obecný postup 1. Volba typu rozdělení (pokus omyl, zkušenosti, pravděpodobnostní papír) 2. Stanovení statistických charakteristik (parametry teoretických rozdělení) 3. Proložení empirické čáry překročení teoretickou 4. Posouzení úspěšnosti proložení (vizuální posouzení, Kolmogorov-Smirnov, Pearson) 5. V případě neúspěchu návrat na bod 1 (volba jiného typu rozdělení)

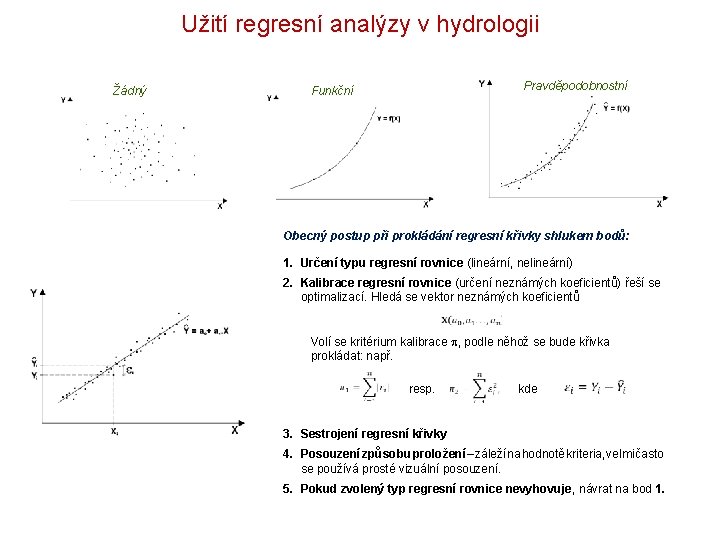
Užití regresní analýzy v hydrologii Žádný Pravděpodobnostní Funkční Obecný postup při prokládání regresní křivky shlukem bodů: 1. Určení typu regresní rovnice (lineární, nelineární) 2. Kalibrace regresní rovnice (určení neznámých koeficientů) řeší se optimalizací. Hledá se vektor neznámých koeficientů Volí se kritérium kalibrace , podle něhož se bude křivka prokládat: např. resp. kde 3. Sestrojení regresní křivky 4. Posouzení způsobu proložení – záleží na hodnotě kriteria, velmi často se používá prosté vizuální posouzení. 5. Pokud zvolený typ regresní rovnice nevyhovuje, návrat na bod 1.

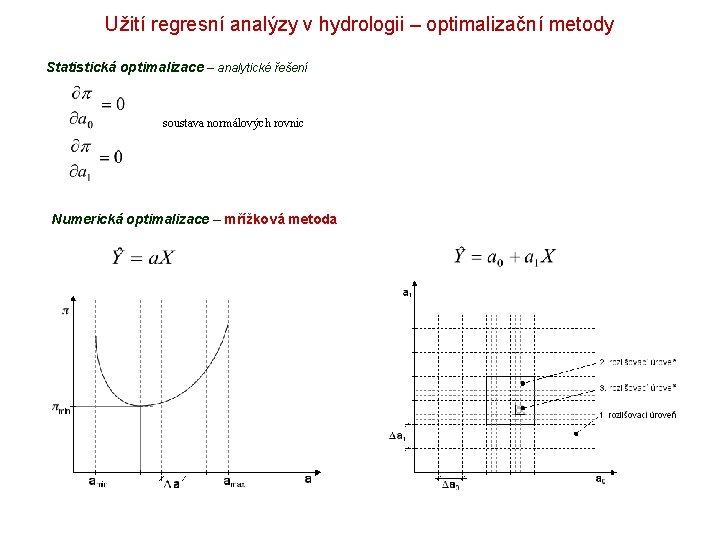
Užití regresní analýzy v hydrologii – optimalizační metody Statistická optimalizace – analytické řešení soustava normálových rovnic Numerická optimalizace – mřížková metoda

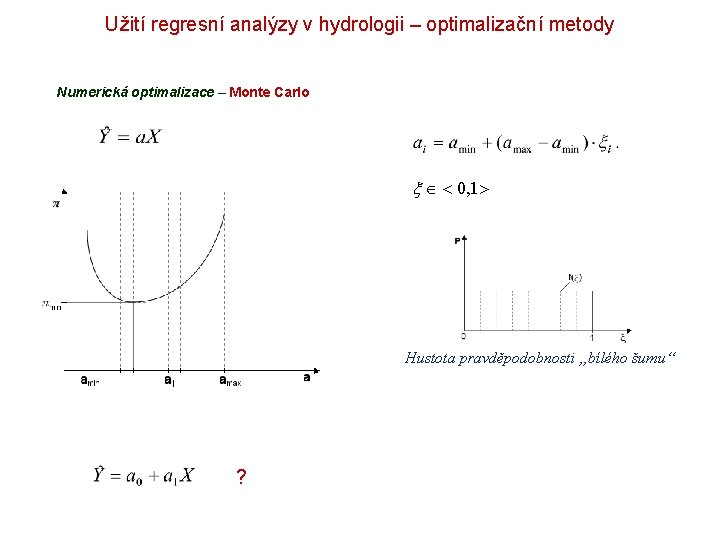
Užití regresní analýzy v hydrologii – optimalizační metody Numerická optimalizace – Monte Carlo 0, 1 Hustota pravděpodobnosti „bílého šumu“ ?

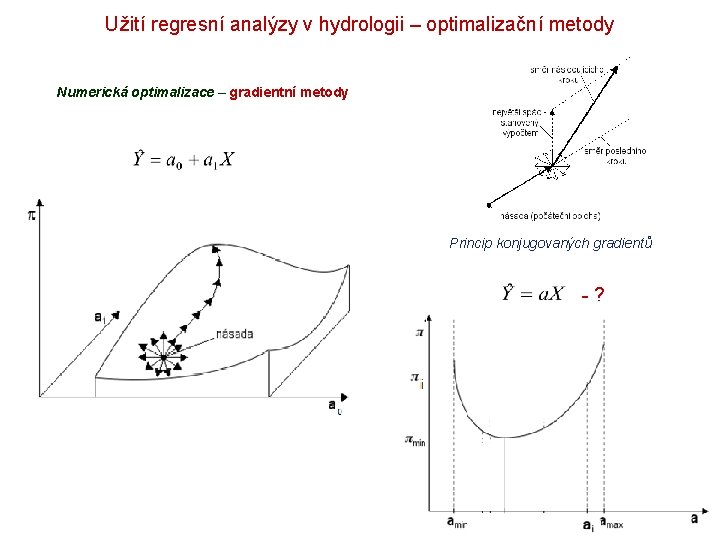
Užití regresní analýzy v hydrologii – optimalizační metody Numerická optimalizace – gradientní metody Princip konjugovaných gradientů -?

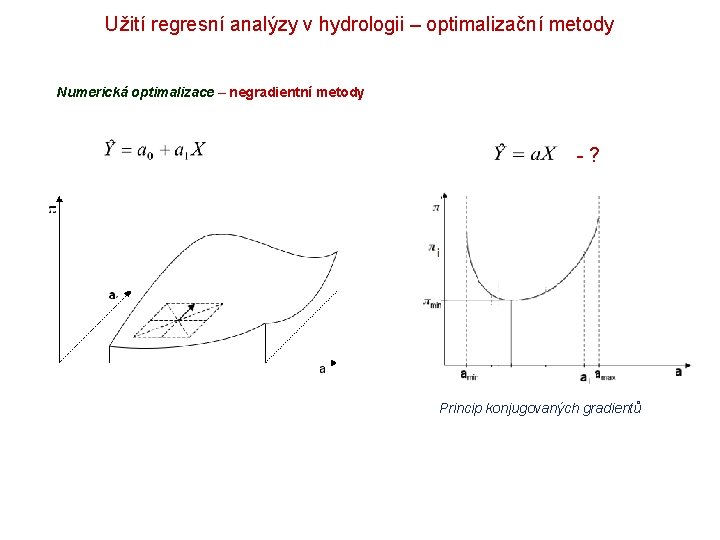
Užití regresní analýzy v hydrologii – optimalizační metody Numerická optimalizace – negradientní metody -? Princip konjugovaných gradientů

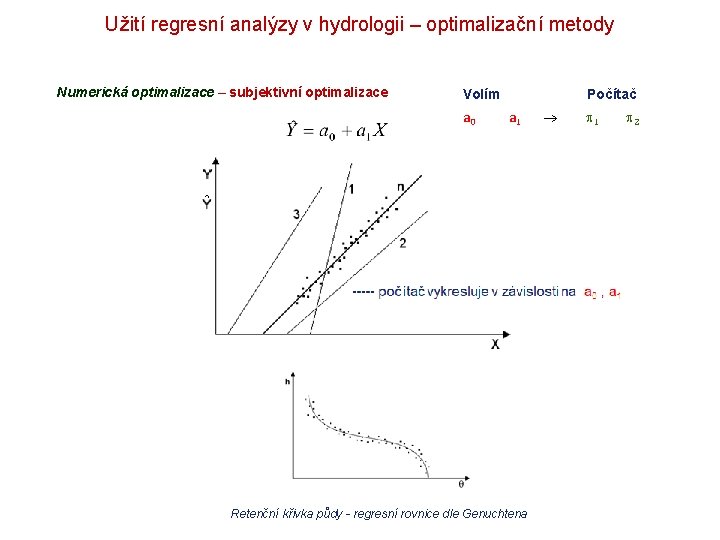
Užití regresní analýzy v hydrologii – optimalizační metody Numerická optimalizace – subjektivní optimalizace Volím a 0 Počítač a 1 Retenční křivka půdy - regresní rovnice dle Genuchtena 1 2

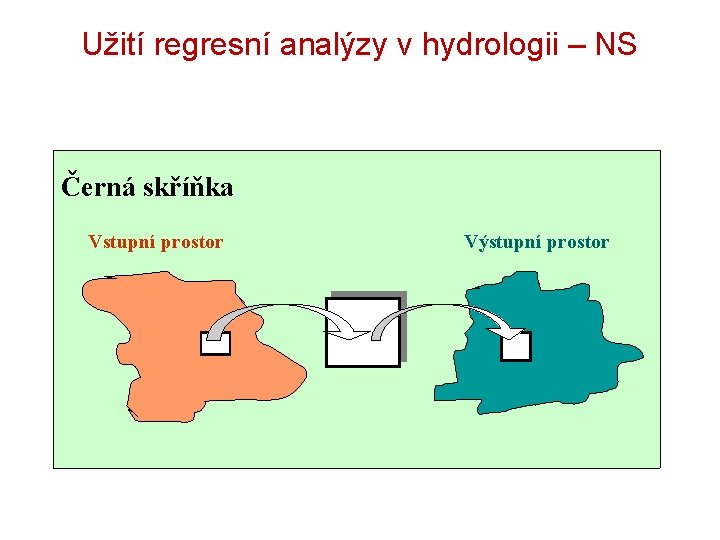
Užití regresní analýzy v hydrologii – NS Černá skříňka Vstupní prostor Výstupní prostor

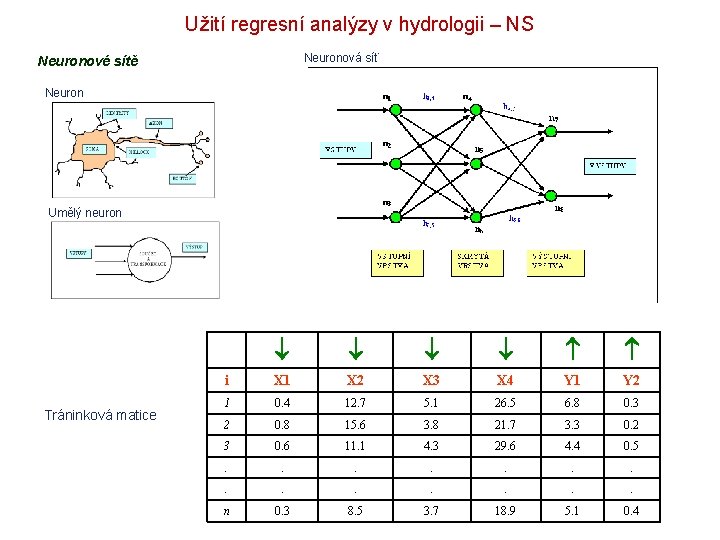
Užití regresní analýzy v hydrologii – NS Neuronová síť Neuronové sítě Neuron Umělý neuron Tráninková matice i X 1 X 2 X 3 X 4 Y 1 Y 2 1 0. 4 12. 7 5. 1 26. 5 6. 8 0. 3 2 0. 8 15. 6 3. 8 21. 7 3. 3 0. 2 3 0. 6 11. 1 4. 3 29. 6 4. 4 0. 5 . . . n 0. 3 8. 5 3. 7 18. 9 5. 1 0. 4

Užití regresní analýzy v hydrologii – GA Genetické algoritmy Jedinec (jeden chromozom), populace, generace • Reprodukce – z počáteční populace jedinců (rodičů) pomocí křížení a mutace vzniká další generace jedinců. Výběr rodičů – selekce. Geny rodičů určují chromozom nového jedince (poloha bodu v prohledávaném prostoru). Operátory GA • Binární kódování chromozomů Chromozom A 1011001101110 Chromozom B 1111110000110100111 Kódování pomocí hodnot Chromozom A 1. 54 2. 47 5. 18 2. 36 8. 48 3. 14 5. 67 Chromozom B 1. 64 2. 41 5. 49 2. 11 8. 01 3. 95 5. 13 Stromové kódování - NS • Křížení Potomek 1 Potomek 2 1011001011110100111 1111110000001101110 • Mutace (pouze určité procento jedinců) Mut. pot. 1 1011001111110100111 • Elitismus

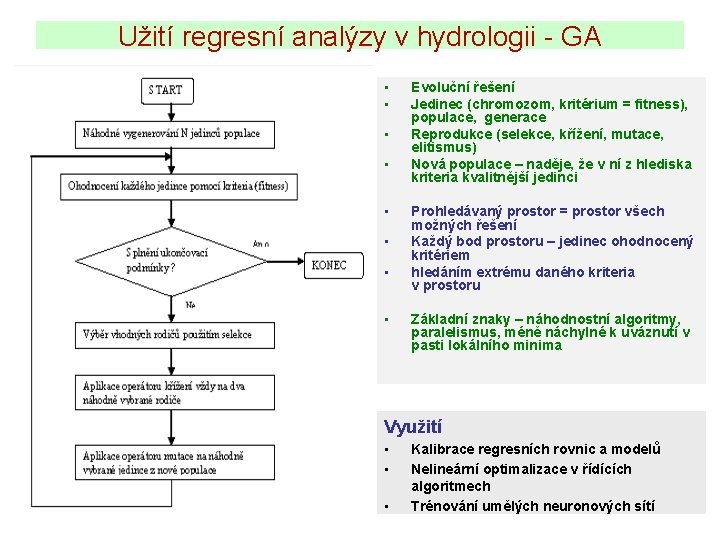
Užití regresní analýzy v hydrologii - GA • • Evoluční řešení Jedinec (chromozom, kritérium = fitness), populace, generace Reprodukce (selekce, křížení, mutace, elitismus) Nová populace – naděje, že v ní z hlediska kriteria kvalitnější jedinci Prohledávaný prostor = prostor všech možných řešení Každý bod prostoru – jedinec ohodnocený kritériem hledáním extrému daného kriteria v prostoru Základní znaky – náhodnostní algoritmy, paralelismus, méně náchylné k uváznutí v pasti lokálního minima Využití • • • Kalibrace regresních rovnic a modelů Nelineární optimalizace v řídících algoritmech Trénování umělých neuronových sítí

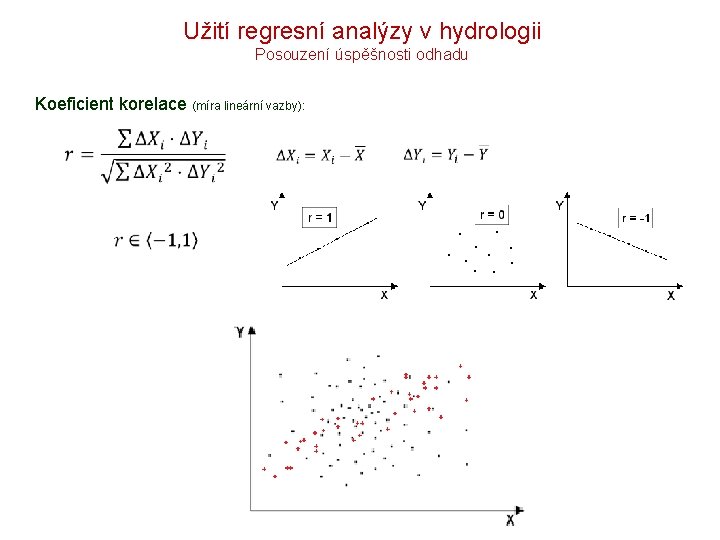
Užití regresní analýzy v hydrologii Posouzení úspěšnosti odhadu Koeficient korelace (míra lineární vazby):

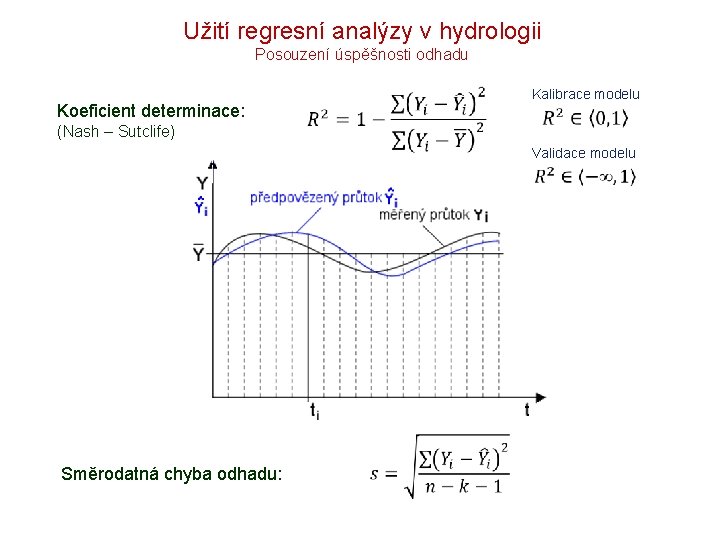
Užití regresní analýzy v hydrologii Posouzení úspěšnosti odhadu Koeficient determinace: Kalibrace modelu (Nash – Sutclife) Validace modelu Směrodatná chyba odhadu:

Časové řady v hydrologii

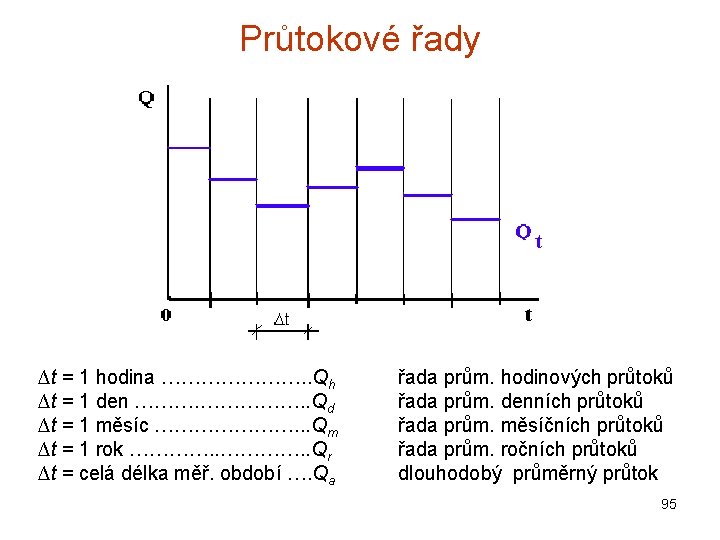
Průtokové řady ∆t = 1 hodina …………………. . Qh ∆t = 1 den ……………. . Qd ∆t = 1 měsíc …………………. . . Qm ∆t = 1 rok …………. . Qr ∆t = celá délka měř. období …. Qa řada prům. hodinových průtoků řada prům. denních průtoků řada prům. měsíčních průtoků řada prům. ročních průtoků dlouhodobý průměrný průtok 95

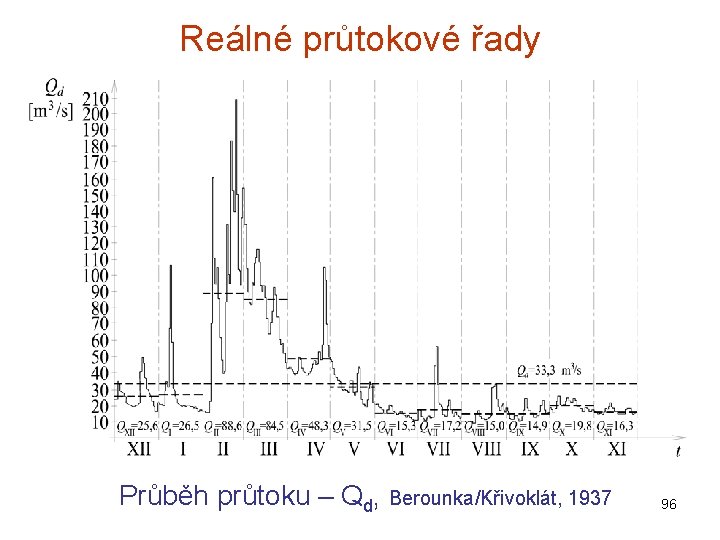
Reálné průtokové řady Průběh průtoku – Qd, Berounka/Křivoklát, 1937 96

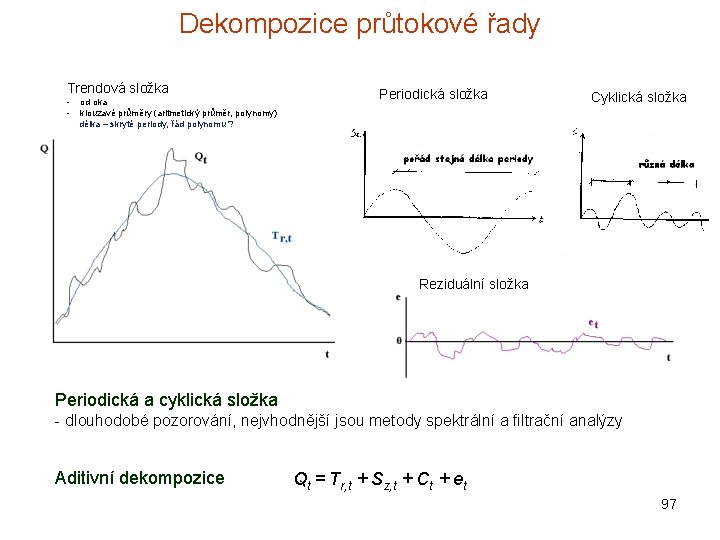
Dekompozice průtokové řady Trendová složka - od oka klouzavé průměry (aritmetický průměr, polynomy) délka – skryté periody, řád polynomu ? Periodická složka Cyklická složka Reziduální složka Periodická a cyklická složka - dlouhodobé pozorování, nejvhodnější jsou metody spektrální a filtrační analýzy Aditivní dekompozice Qt = Tr, t + Sz, t + Ct + et 97

Vnitřní struktura průtokové řady Autokorelační funkce 98

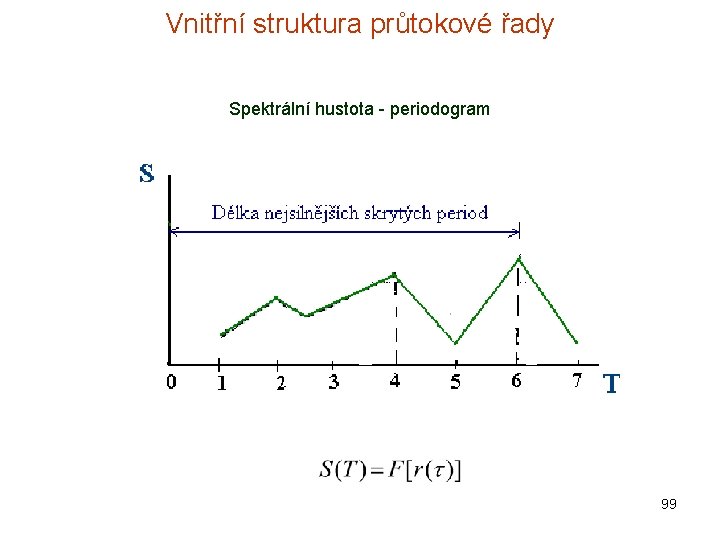
Vnitřní struktura průtokové řady Spektrální hustota - periodogram 99

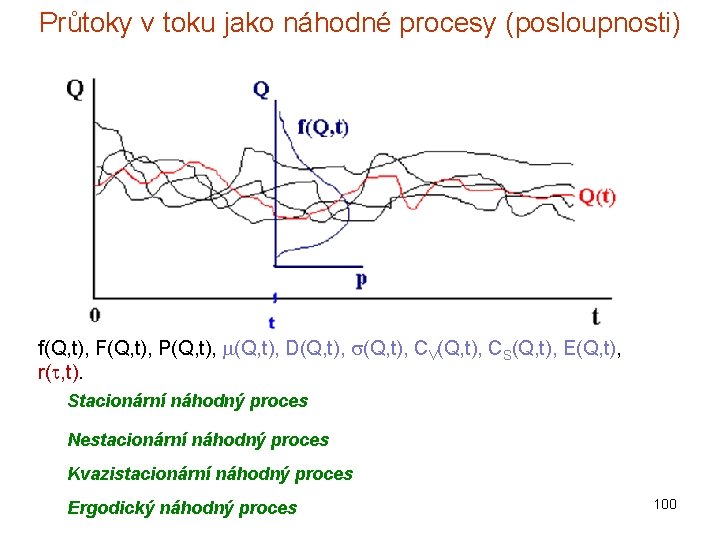
Průtoky v toku jako náhodné procesy (posloupnosti) f(Q, t), F(Q, t), P(Q, t), D(Q, t), CV(Q, t), CS(Q, t), E(Q, t), r( , t). Stacionární náhodný proces Nestacionární náhodný proces Kvazistacionární náhodný proces Ergodický náhodný proces 100

Zvýšení reprezentativnosti průtokových řad • Maximální délka • Metoda momentů • Prověřování homogenity • Oprava extrémů • Oprava vychýlení statistických charakteristik 101

Rozdělení průtokových řad Umělá (syntetická) Průtoková řada Měřená Reálná Odvozená 102

Umělé průtokové řady Z reálné průtokové řady, popsané: f(Q, t), F(Q, t), P(Q, t), D(Q, t), CV(Q, t), CS(Q, t), E(Q, t), r( , t) , generujeme velmi dlouhou umělou průtokovou řadu, popsanou: f(Q, t), F(Q, t), P(Q, t), D(Q, t), CV(Q, t), CS(Q, t), E(Q, t), r( , t). Dobrý generátor: shoda mezi popisujícími veličinami reálné a umělé průtokové řady 103

Umělé průtokové řady – princip generování Generátory umělých průtokových řad - průměrných ročních průtoků (čára překročení, Svanidze – Reznikovskij, lineární regresní model) průměrných měsíčních průtoků (lineární regresní model, metoda fragmentů, LT-AR, LN-AR, ARMA) Měsíční průtoky Roční průtoky Generátory umělých průtokových řad v systému stanic (metoda centrální a satelitních stanic, metoda ortogonální transformace, LRM)

Odvozování průtokových řad - v poměru dlouhodobých průměrných průtoků Řada průměrných ročních průtoků: Řada průměrných měsíčních průtoků: pro i = 1, 2, … n - pomocí srážkoodtokových úhrnných křivek Řada průměrných ročních průtoků: Řada průměrných měsíčních průtoků: 105

Třídy spolehlivosti průtokových řad • 1. třída – měrný profil (nejvyšší spolehlivost) Průtokové řady odvozeny: • 2. třída – pro posunutý profil na stejném toku, kde již existuje měrný profil • 3. třída – profil, který leží na přítoku do toku, na kterém již existuje měrný profil • 4. třída – průtok odvozen analogií z jiného povodí 106

Dlouhodobý průměrný průtok Qa Měření – střední hodnota Bilanční rovnice Podélný profil dlouhodobých průměrných průtoků Metoda izolinií specifického odtoku 107

Režim vodních toků • Průtok přirozený: průtok vody v toku s přirozeným hydrologickým režimem (neovlivněný např. vzdutím hladiny vlivem vodní stavby) • Průtok ovlivněný: průtok vody v toku s ovlivněným hydrologickým režimem • Průtok setrvalý: průtok, který se po delší dobu výrazně nemění • Průtok nalepšený: průtok záměrně zvětšený nad hodnotu přirozeného průtoku, např. doplňováním vody do toku z nádrže • Průtok průměrný: střední hodnota průtoku za uvažované období • Maximální průtok Qmax : největší (kulminační) průtok povodňové vlny v určitém období (den měsíc, rok, řada let) • N-letý maximální průtok QN : největší (kulminační) průtok povodňové vlny, který je dosažen nebo překročen v dlouhodobém průměru jednou za N let. (Q 1, Q 2, Q 5, Q 10, Q 20, Q 50, Q 100) • Minimální průtok Qmin : nejmenší průměrný denní průtok v určeném období (den měsíc, rok, řada let) • N-letý minimální průtok QN, min : nejmenší průměrný denní průtok, který je dosažen nebo nedostoupen průměrně jednou za N let 108

Klasifikace vodnosti jednotlivých roků Podklad – čára překročení průměrných ročních průtoků 109

Extrémní průtoky

Maximální průtoky Povodeň Přechodné výrazné zvýšení hladiny vodního toku způsobené náhlým zvýšením průtoku nebo dočasným zmenšením průtočnosti koryta, při kterém hrozí vylití vody z koryta nebo při kterém se voda z koryta vylévá a může způsobit škody Příčiny vzniku povodní • SOP – přívalové srážky v malých povodích • SOP – regionální srážky (tání sněhové pokrývky, resp. mix) ve středně velkých a velkých povodích • Ledové nápěchy v zúžených průtočných profilech na tocích 111

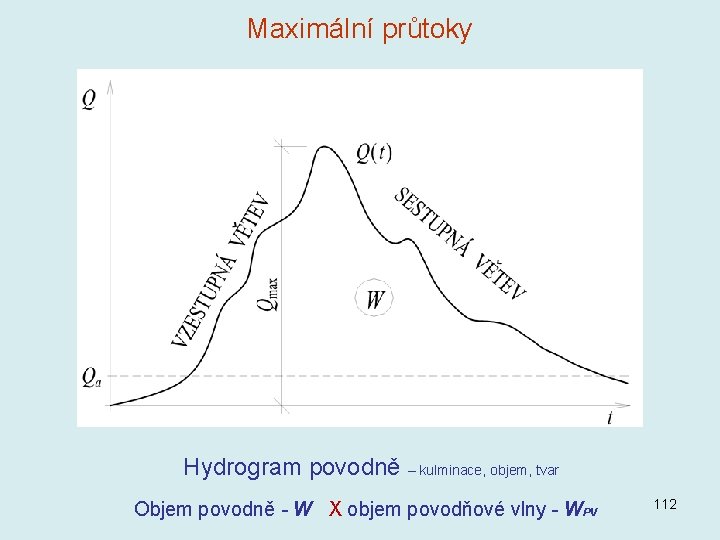
Maximální průtoky Hydrogram povodně – kulminace, objem, tvar Objem povodně - W X objem povodňové vlny - WPV 112

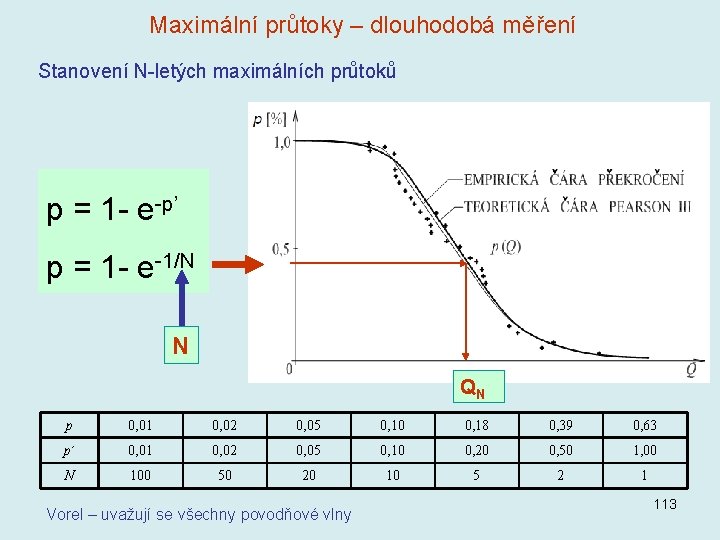
Maximální průtoky – dlouhodobá měření Stanovení N-letých maximálních průtoků p = 1 - e-p’ p = 1 - e-1/N N QN p 0, 01 0, 02 0, 05 0, 10 0, 18 0, 39 0, 63 p´ 0, 01 0, 02 0, 05 0, 10 0, 20 0, 50 1, 00 N 100 50 20 10 5 2 1 Vorel – uvažují se všechny povodňové vlny 113

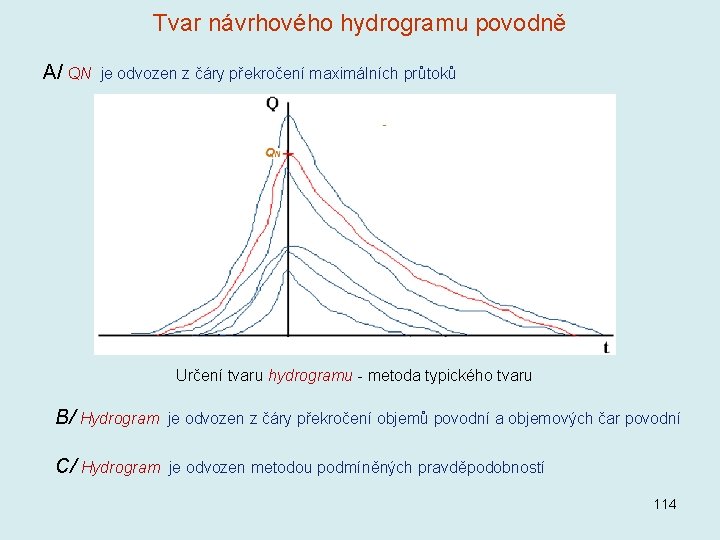
Tvar návrhového hydrogramu povodně A/ QN je odvozen z čáry překročení maximálních průtoků Určení tvaru hydrogramu - metoda typického tvaru B/ Hydrogram je odvozen z čáry překročení objemů povodní a objemových čar povodní C/ Hydrogram je odvozen metodou podmíněných pravděpodobností 114

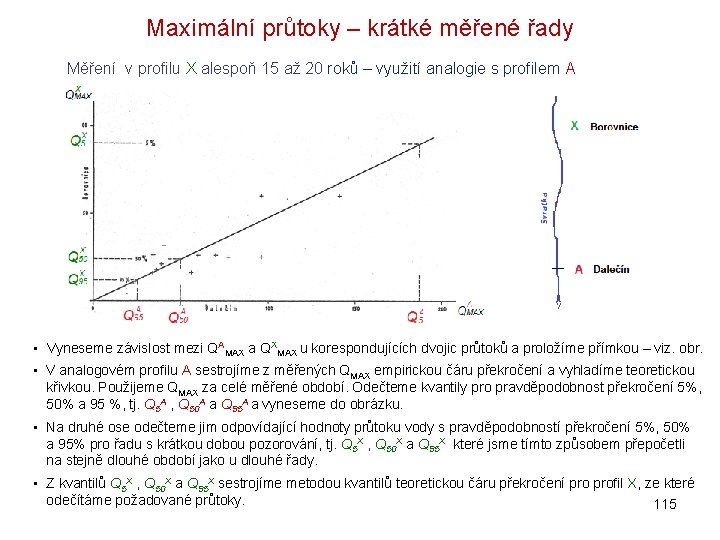
Maximální průtoky – krátké měřené řady Měření v profilu X alespoň 15 až 20 roků – využití analogie s profilem A • Vyneseme závislost mezi QAMAX a QXMAX u korespondujících dvojic průtoků a proložíme přímkou – viz. obr. • V analogovém profilu A sestrojíme z měřených QMAX empirickou čáru překročení a vyhladíme teoretickou křivkou. Použijeme QMAX za celé měřené období. Odečteme kvantily pro pravděpodobnost překročení 5%, 50% a 95 %, tj. Q 5 A , Q 50 A a Q 95 A a vyneseme do obrázku. • Na druhé ose odečteme jim odpovídající hodnoty průtoku vody s pravděpodobností překročení 5%, 50% a 95% pro řadu s krátkou dobou pozorování, tj. Q 5 X , Q 50 X a Q 95 X které jsme tímto způsobem přepočetli na stejně dlouhé období jako u dlouhé řady. • Z kvantilů Q 5 X , Q 50 X a Q 95 X sestrojíme metodou kvantilů teoretickou čáru překročení profil X, ze které odečítáme požadované průtoky. 115

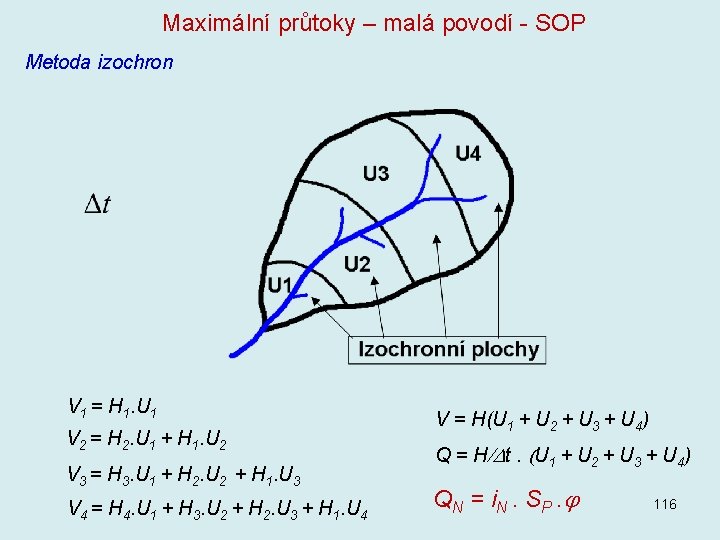
Maximální průtoky – malá povodí - SOP Metoda izochron V 1 = H 1. U 1 V 2 = H 2. U 1 + H 1. U 2 V 3 = H 3. U 1 + H 2. U 2 + H 1. U 3 V 4 = H 4. U 1 + H 3. U 2 + H 2. U 3 + H 1. U 4 V = H(U 1 + U 2 + U 3 + U 4) Q = H/ t. (U 1 + U 2 + U 3 + U 4) QN = i N. S P. 116

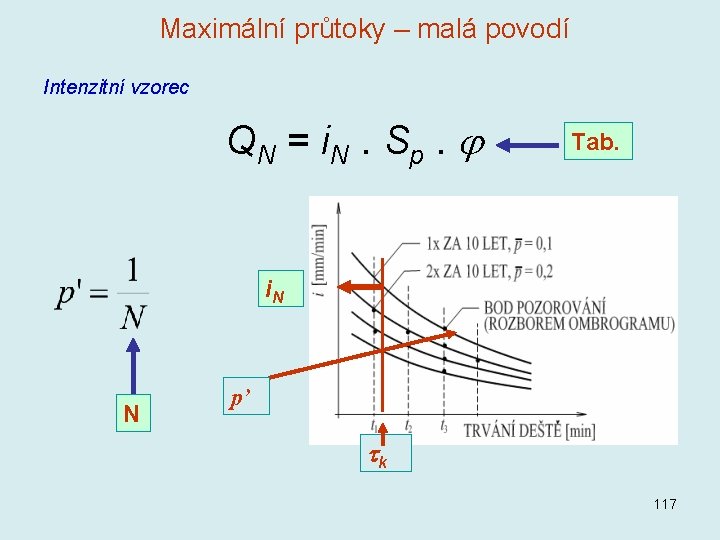
Maximální průtoky – malá povodí Intenzitní vzorec Q N = i. N. S p. Tab. i. N N p’ k 117

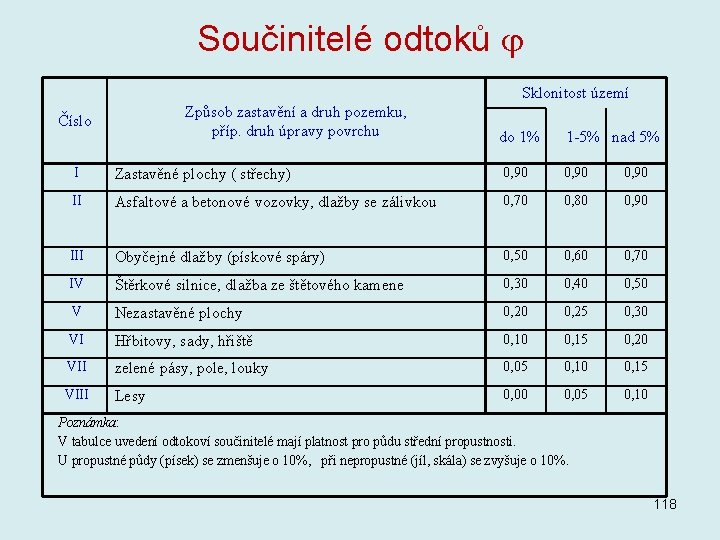
Součinitelé odtoků Sklonitost území Způsob zastavění a druh pozemku, příp. druh úpravy povrchu Číslo do 1% 1 -5% nad 5% I Zastavěné plochy ( střechy) 0, 90 II Asfaltové a betonové vozovky, dlažby se zálivkou 0, 70 0, 80 0, 90 III Obyčejné dlažby (pískové spáry) 0, 50 0, 60 0, 70 IV Štěrkové silnice, dlažba ze štětového kamene 0, 30 0, 40 0, 50 V Nezastavěné plochy 0, 20 0, 25 0, 30 VI Hřbitovy, sady, hřiště 0, 10 0, 15 0, 20 VII zelené pásy, pole, louky 0, 05 0, 10 0, 15 VIII Lesy 0, 00 0, 05 0, 10 Poznámka: V tabulce uvedení odtokoví součinitelé mají platnost pro půdu střední propustnosti. U propustné půdy (písek) se zmenšuje o 10%, při nepropustné (jíl, skála) se zvyšuje o 10%. 118

Odtokové poměry Součinitel odtoku Specifický odtok Specifické dlouhodobé průměrné odtoky - qa 119

Maximální průtoky – malá povodí Exponenciální vzorce QN = Q 100 N CN - křivky (Des. Q) Vo = H o S P A =1000/CN – 10 potenciální maximální retenci povodí Ia = 0, 2 A počáteční retence povodí v bezodtokové fázi 120

Minimální průtoky Absolutní minimální průtok (okamžitý průtok) - Qabs min N-letý minimální průtok (průměrné denní průtoky) - QN, min – čára nedostoupení m - denní vody (průměrné denní průtoky) - Qmd – čára překročení Minimální zůstatkový průtok Vzorce Iszkowského vztah - Analogie Q 355 d , Q 330 d Q 20, min Q 50, min Q 100, min Q 270 d Q 355 d Q 364 d Q 10, min

Předpovědi vodních stavů a průtoků • Formální zápis předpovědního modelu • Pravděpodobnostní charakter předpovědí Rozdělení předpovědí • • Termínované a netermínované Statistické, genetické, kombinované Hydrometrické a hydrometeorologické Dlouhodobé, střednědobé, krátkodobé, operativní 122

Předpovědi vodních stavů a průtoků Dlouhodobé předpovědi • • • Regresní rovnice Regresní modely Klouzavé průměry Harmonická analýza Učící se modely (NS) 123

Předpovědi vodních stavů a průtoků Střednědobé předpovědi • • • Regresní rovnice Regresní modely Klouzavé průměry Harmonická analýza Odtok z tání sněhové pokrývky Málovodá období – výtokové křivky 124

Předpovědi vodních stavů a průtoků Krátkodobé předpovědi I. Hydrometrické předpovědi • Metoda tendencí • Metoda odpovídajících si průtoků • Muskingum II. Hydrodynamické předpovědi • Saint_Venant III. Hydrometeorologické předpovědi • Malá povodí : Hs Ho hydrogram Ho = . Hs, hydrogram: Ho = f (Hs, , týden, API ) - RR, KK, NS, CN trojúhelník, izochrony, JH 125

Předpovědi vodních stavů a průtoků Krátkodobé předpovědi - pokračování III. Hydrometeorologické předpovědi • Střední a velká povodí Koncepční regresní modely (Bilan, Sacramento, Aqualog) 126

Předpovědi vodních stavů a průtoků Krátkodobé předpovědi - pokračování III. Hydrometeorologické předpovědi • Střední a velká povodí Kinematická vlnová aproximace (Hydrog) 127

Podpovrchové vody – samostudium • Co rozumíme nasycenou a nenasycenou zónou • Teorie vzniku podpovrchových vod • Druhy podpovrchových vod • Rozdělení pramenů • Měření vydatnosti a stálosti pramenů • Měření polohy hladin podzemních vod v sondách

Splaveniny – samostudium • Co rozumíme plaveninami a dnovými splaveninami • Kdy dochází k usazování plavenin • Útvary, které vytváří dnové splaveniny • Měření plavenin • Měření dnových splavenin

Závěr