Hybrid quantum decoupling and error correction Leonid Pryadko

Outline • Motivation: QEC and encoded dynamical decoupling with correlated noise • General results on dynamical decoupling • Concurrent application of logic • Intercalated application of logic • Conclusions and perspective

Stabilizer QECC • Error correction is done by measuring the stabilizers frequently and correcting with the corresponding error operators if needed • QECC period should be small compared to the decoherence rate • Traditional QECCs: – Expensive: need many ancillas, fast measurement, processing & correcting – May not work well with correlated environment

QECC with constant error terms [[3, 1, 3]] 1 qubit [[5, 1, 3]] [[5, 1, 5]]

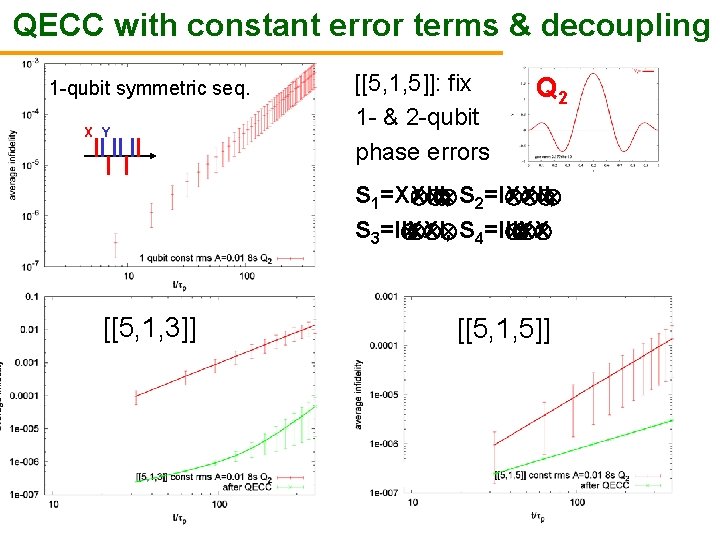
QECC with constant error terms & decoupling 1 -qubit symmetric seq. X Y [[5, 1, 5]]: fix 1 - & 2 -qubit phase errors Q 2 S 1=X X I I I, S 2=I X X I I, S 3=I I X X I, S 4=I I I X X [[5, 1, 3]] [[5, 1, 5]]

Combined coherence protection technique • Passive: Dynamical Decoupling – Effective with low-frequency bath – Most frugal with ancilla qubits needed – Needs fast pulsing (resource used: bandwidth) • Active: Quantum error correcting codes – – Most universal Needs many ancilla qubits Needs fast measurement, processing & correcting Expensive • Combined: Encoded Dynamical Recoupling [Viola, Lloyd & Knill (1999)] – Better suppression of decoherence due to slow environment potentially much more efficient – Control can be done along with decoupling

Example with hard pulses & constant errors • Errors are fully reversed at the end of the decoupling cycle 1 2 • Normalizer and stabilizer commute – add logic anywhere!? 1 2 XL YL ZL

Example with hard pulses & constant errors • Errors are fully reversed at the end of the decoupling cycle 1 2 • Normalizer and stabilizer commute – add logic anywhere! 1 2 XL XL YL YL ZL ZL

Error operators in rotating frame • S: system, E: environment, DD: dynamical decoupling • Dynamical decoupling is dominant: is large • Solve controlled dynamics and write the Hamiltonian in the interaction representation with respect to DD • Interaction representation with respect to environment • Bath coupling is now modulated at the combination of the environment and dynamical decoupling frequencies • With first-order average Hamiltonian suppressed, all S+E coupling is shifted to high frequences no T 1 processes (Kofman & Kurizki, 2001)

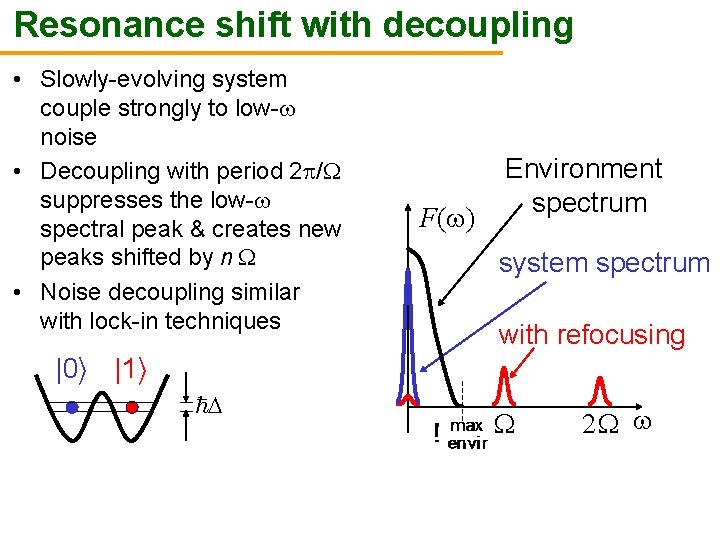
Resonance shift with decoupling • Slowly-evolving system couple strongly to low- noise • Decoupling with period 2 / suppresses the low- spectral peak & creates new peaks shifted by n • Noise decoupling similar with lock-in techniques F( ) Environment spectrum system spectrum with refocusing |0 i |1 i ~ 2

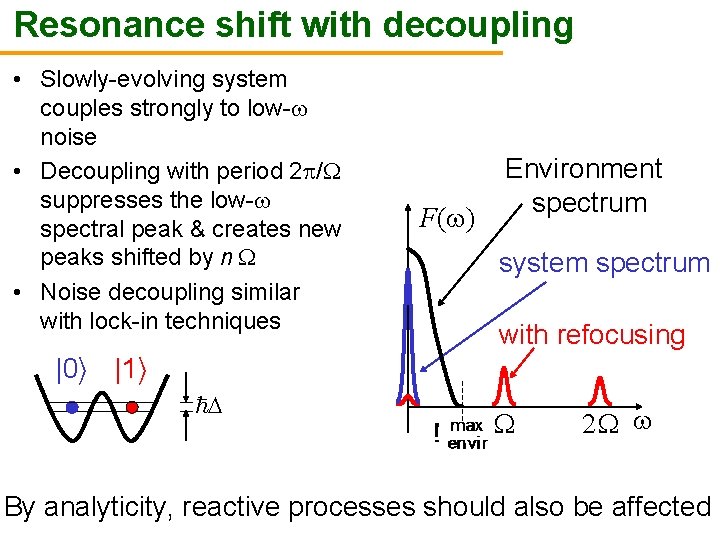
Resonance shift with decoupling • Slowly-evolving system couples strongly to low- noise • Decoupling with period 2 / suppresses the low- spectral peak & creates new peaks shifted by n • Noise decoupling similar with lock-in techniques F( ) Environment spectrum system spectrum with refocusing |0 i |1 i ~ 2 By analyticity, reactive processes should also be affected

Quantum kinetics with DD: results • K=0 (no DD): Dephasing rate 0» max(J, (0) 0), (t)=||h. B (t)B (0)i|| • K=1 (1 st order): Single-phonon decay eliminated Dephasing rate 1» max(J 2 , (0) ), plus effect of higher order derivatives of (t) at t=0. Reduction by factor / 0 • K=2 (2 nd order): all derivatives disappear Exponential reduction in / 0 • Visibility reduction » (0) 2 (generic sequence) » ’’(0) 4 » (0) 4/ 02 (symmetric sequence) (LPP & P. Sengupta, 2006)

Encoded dynamical recoupling • Several physical qubits logical • Operators from the stabilizer are used for dynamical decoupling ( ), at the same time running logic operators from • It is important that commute (Viola, Lloyd & Knill, 1999) mutually

No-resonance condition for T 1 processes mutually commute • Interaction representation • Combination of three rotation frequencies – Harmonics of DD (periodic) – L (can be small since logic is not periodic) – E (limited from above by Emax) • State decay through environment is suppressed if

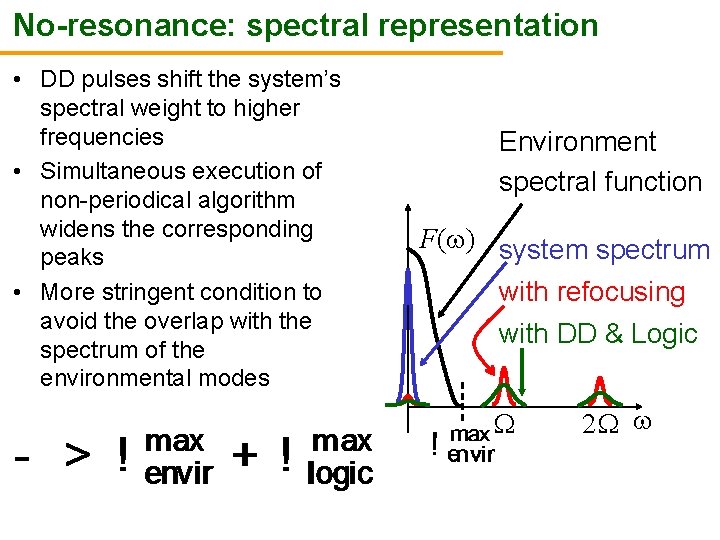
No-resonance: spectral representation • DD pulses shift the system’s spectral weight to higher frequencies • Simultaneous execution of non-periodical algorithm widens the corresponding peaks • More stringent condition to avoid the overlap with the spectrum of the environmental modes Environment spectral function F( ) system spectrum with refocusing with DD & Logic 2

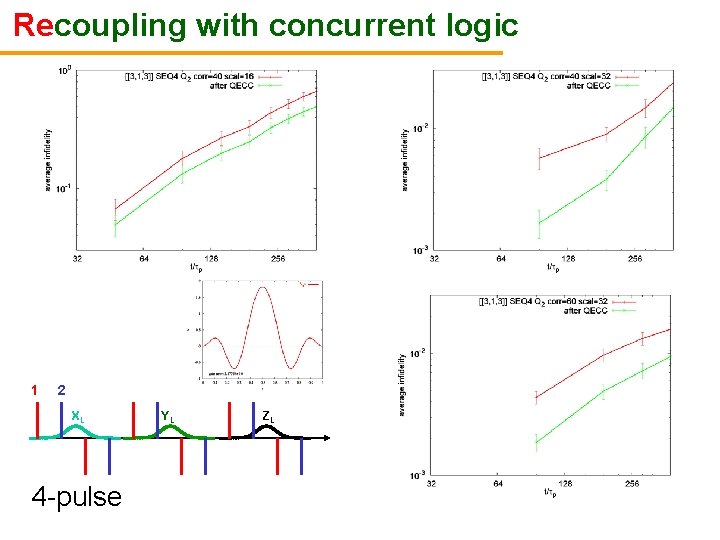
Recoupling with concurrent logic 1 2 XL 4 -pulse YL ZL

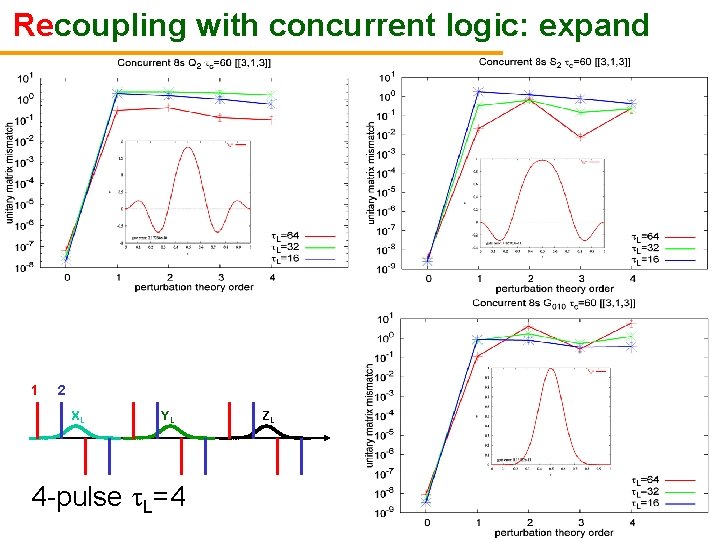
Recoupling with concurrent logic: expand 1 2 XL YL 4 -pulse L=4 ZL

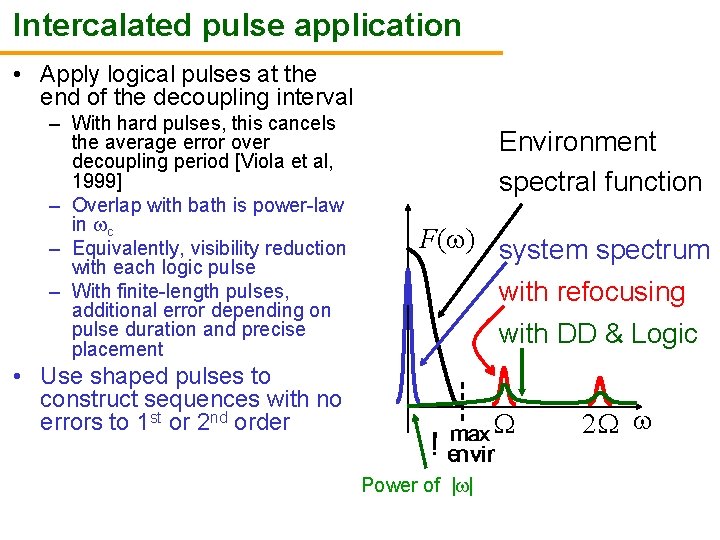
Intercalated pulse application • Apply logical pulses at the end of the decoupling interval – With hard pulses, this cancels the average error over decoupling period [Viola et al, 1999] – Overlap with bath is power-law in c – Equivalently, visibility reduction with each logic pulse – With finite-length pulses, additional error depending on pulse duration and precise placement Environment spectral function F( ) system spectrum with refocusing with DD & Logic • Use shaped pulses to construct sequences with no errors to 1 st or 2 nd order Power of | | 2

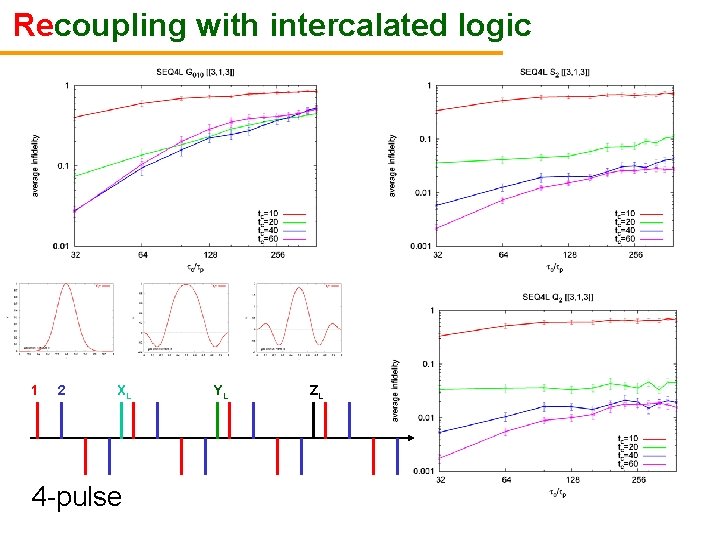
Recoupling with intercalated logic 1 2 XL 4 -pulse YL ZL

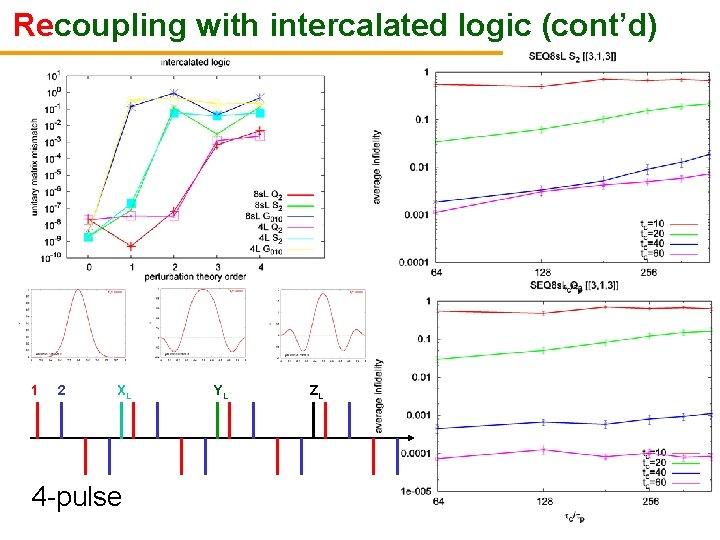
Recoupling with intercalated logic (cont’d) 1 2 XL 4 -pulse YL ZL

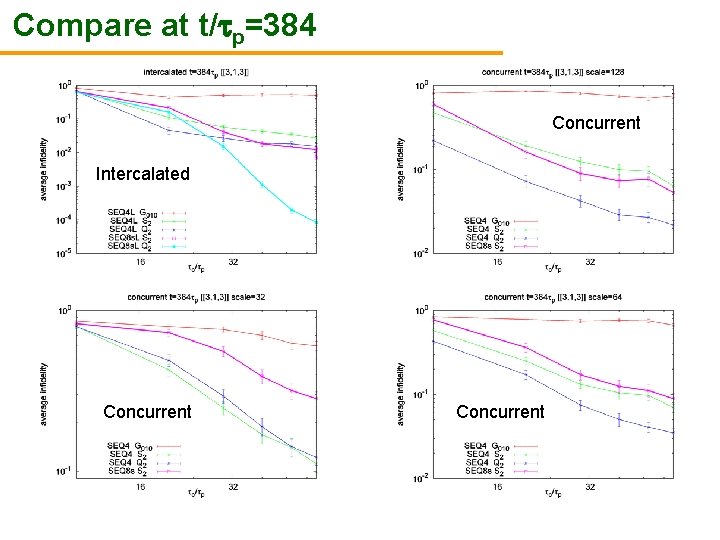
Compare at t/ p=384 Concurrent Intercalated Concurrent

Conclusions and Outlook • Much mileage can be gained from carefully engineered concatenation – With decoupling at the lowest level, need careful pulse placement, pulse & sequence design • Bandwidth is used to combine logic and decoupling • Still to confirm predicted parameter scaling • Analyze effects of: – Actual many-qubit gates needed – Fast decoherence addition – QEC dynamics (gates with ancillas, measurement, …) • Can fault-tolerance be achieved in this scheme?