Hwajung Lee ITEC 452 Distributed Computing Lecture 10

Hwajung Lee ITEC 452 Distributed Computing Lecture 10 Graph Algorithms

Graph Algorithms Why graph algorithms ? It is not a “graph theory” course! Many problems in networks can be modeled as graph problems. Note that - The topology of a distributed system is a graph. - Routing table computation uses the shortest path algorithm Efficient broadcasting uses a spanning tree Maxflow algorithm determines the maximum flow between a pair of nodes in a graph.

Routing Shortest path routing Distance vector routing Link state routing Routing in sensor networks Routing in peer-to-peer networks
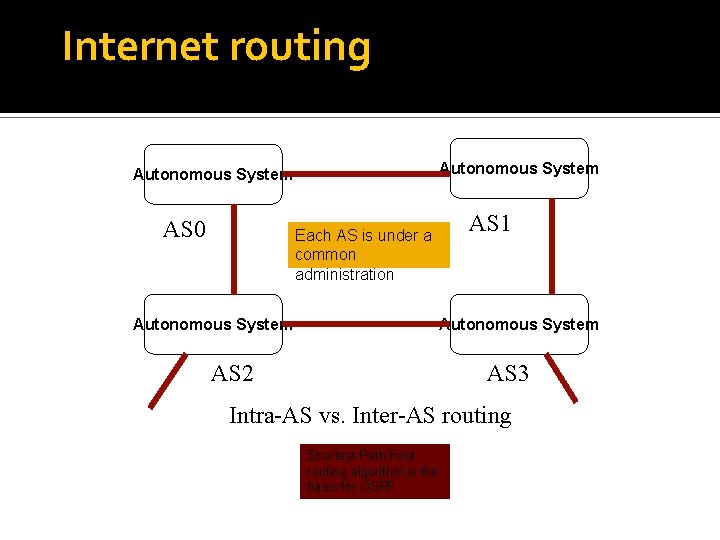
Internet routing Autonomous System AS 0 Each AS is under a common administration Autonomous System AS 1 Autonomous System AS 2 AS 3 Intra-AS vs. Inter-AS routing Shortest Path First routing algorithm is the basis for OSPF
Routing revisited (borrowed from Cisco documentation http: //www. cisco. com)
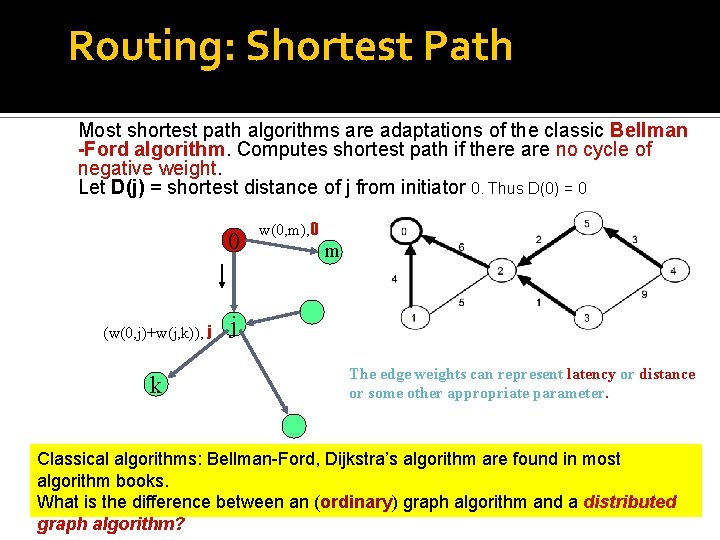
Routing: Shortest Path Most shortest path algorithms are adaptations of the classic Bellman -Ford algorithm. Computes shortest path if there are no cycle of negative weight. Let D(j) = shortest distance of j from initiator 0. Thus D(0) = 0 0 (w(0, j)+w(j, k)), j k w(0, m), 0 m j The edge weights can represent latency or distance or some other appropriate parameter. Classical algorithms: Bellman-Ford, Dijkstra’s algorithm are found in most algorithm books. What is the difference between an (ordinary) graph algorithm and a distributed graph algorithm?
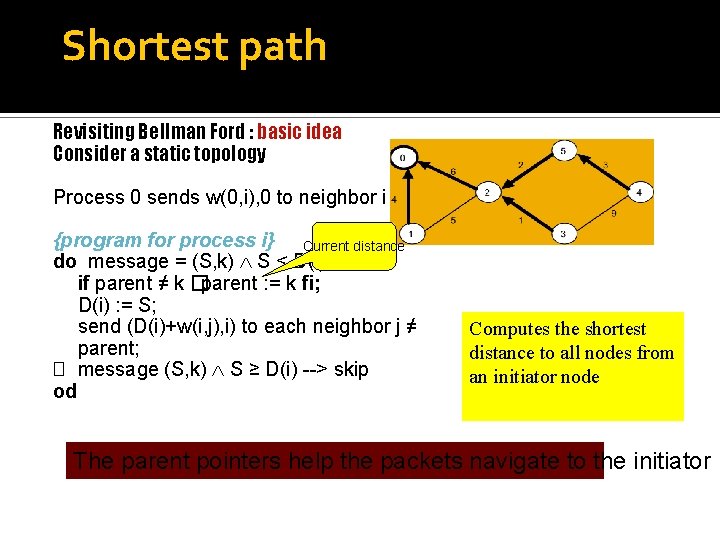
Shortest path Revisiting Bellman Ford : basic idea Consider a static topology Process 0 sends w(0, i), 0 to neighbor i {program for process i} Current distance do message = (S, k) S < D(i) � if parent ≠ k �parent : = k fi; D(i) : = S; send (D(i)+w(i, j), i) to each neighbor j ≠ parent; � message (S, k) S ≥ D(i) --> skip od Computes the shortest distance to all nodes from an initiator node The parent pointers help the packets navigate to the initiator
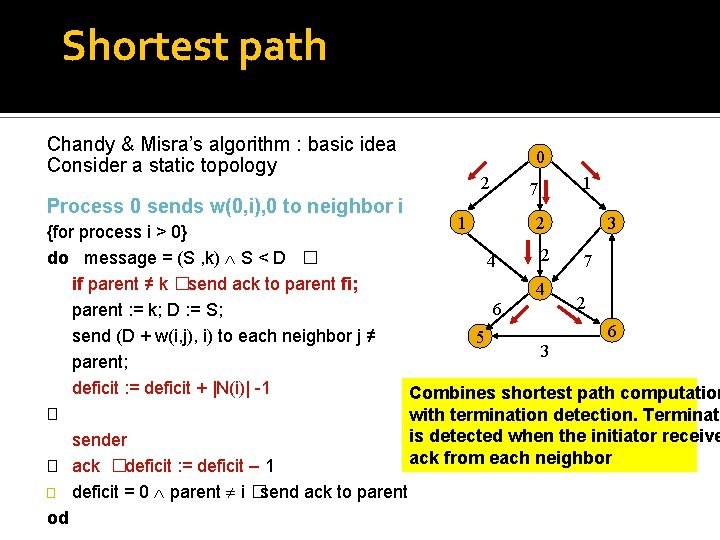
Shortest path Chandy & Misra’s algorithm : basic idea Consider a static topology Process 0 sends w(0, i), 0 to neighbor i 0 2 7 1 1 2 3 {for process i > 0} 2 do message = (S , k) S < D � 4 7 if parent ≠ k �send ack to parent fi; 4 2 6 parent : = k; D : = S; 6 send (D + w(i, j), i) to each neighbor j ≠ 5 3 parent; deficit : = deficit + |N(i)| -1 Combines shortest path computation � with termination detection. Terminati is detected when the initiator receive sender ack from each neighbor � ack �deficit : = deficit – 1 � deficit = 0 parent i � send ack to parent od

Shortest path An important issue is: how well do such algorithms perform when the topology changes? No real network is static! Let us examine distance vector routing that is adaptation of the shortest path algorithm
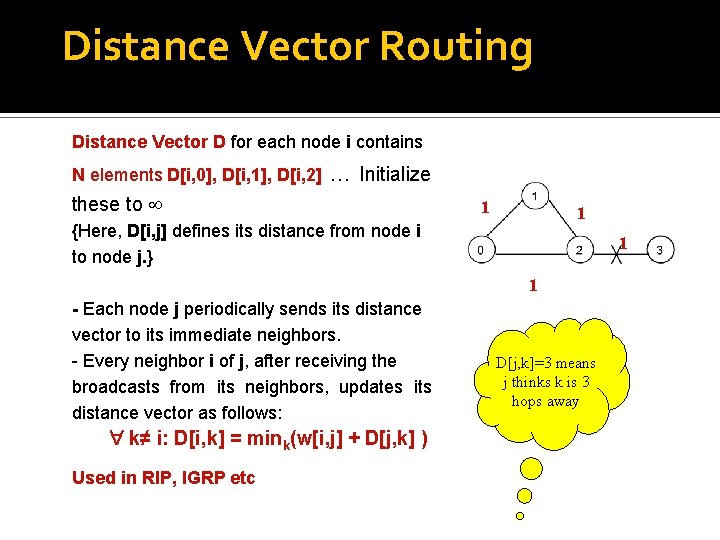
Distance Vector Routing Distance Vector D for each node i contains N elements D[i, 0], D[i, 1], D[i, 2] … Initialize these to 1 1 {Here, D[i, j] defines its distance from node i to node j. } 1 1 - Each node j periodically sends its distance vector to its immediate neighbors. - Every neighbor i of j, after receiving the broadcasts from its neighbors, updates its distance vector as follows: k≠ i: D[i, k] = mink(w[i, j] + D[j, k] ) Used in RIP, IGRP etc D[j, k]=3 means j thinks k is 3 hops away

Counting to infinity Observe what can happen when the link (2, 3) fails. Node 1 thinks d(1, 3) = 2 Node 2 thinks d(2, 3) = d(1, 3)+1 = 3 Node 1 thinks d(1, 3) = d(2, 3)+1 = 4 and so on. So it will take forever for the distances to stabilize. A partial remedy is the split horizon method that will prevent 1 from sending the advertisement about d(1, 3) to 2 since its first hop is node 2 k≠ i: D[i, k] = mink(w[i, j] + D[j, k] Suitable for smaller networks. Larger volume of data is disseminated, but to its immediate neighbors only Poor convergence property

Link State Routing Each node i periodically broadcasts the weights of all edges (i, j) incident on it (this is the link state) to all its neighbors. The mechanism for dissemination is flooding. This helps each node eventually compute the topology of the network, and independently determine the shortest path to any destination node using some standard graph algorithm like Dijkstra’s. Smaller volume data disseminated over the entire network Used in OSPF

Link State Routing Each link state packet has a sequence number seq that determines the order in which the packets were generated. When a node crashes, all packets stored in it are lost. After it is repaired, new packets start with seq = 0. So these new packets may be discarded in favor of the old packets! Problem resolved using TTL

Complexity of Bellman-Ford Theorem. The message complexity of Bellman-Ford algorithm is exponential. Proof outline. Consider a topology with an even number nodes 0 through n-1 (the unmarked edges have weight 0) 1 3 2 k 0 2 n-4 5 2 k-1 4 22 n-2 21 n-5 n-3 20 n-1 Time the arrival of the signals so that D(n-1) reduces from (2 k+1 - 1) to 0 in steps of 1. Since k = (n-1)/2, it will need 2(n+1)/2 -1 messages to reach the goal. So, the message complexity is exponential.
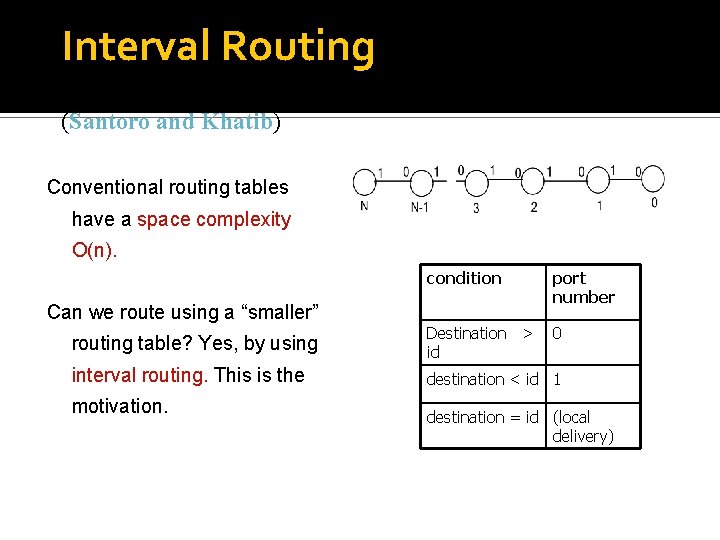
Interval Routing (Santoro and Khatib) Conventional routing tables have a space complexity O(n). condition port number routing table? Yes, by using Destination > id 0 interval routing. This is the destination < id 1 Can we route using a “smaller” motivation. destination = id (local delivery)
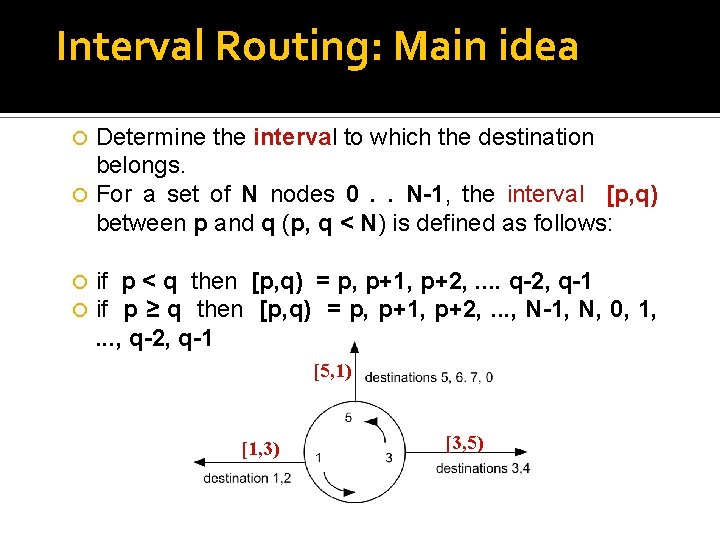
Interval Routing: Main idea Determine the interval to which the destination belongs. For a set of N nodes 0. . N-1, the interval [p, q) between p and q (p, q < N) is defined as follows: if p < q then [p, q) = p, p+1, p+2, . . q-2, q-1 if p ≥ q then [p, q) = p, p+1, p+2, . . . , N-1, N, 0, 1, . . . , q-2, q-1 [5, 1) [1, 3) [3, 5)
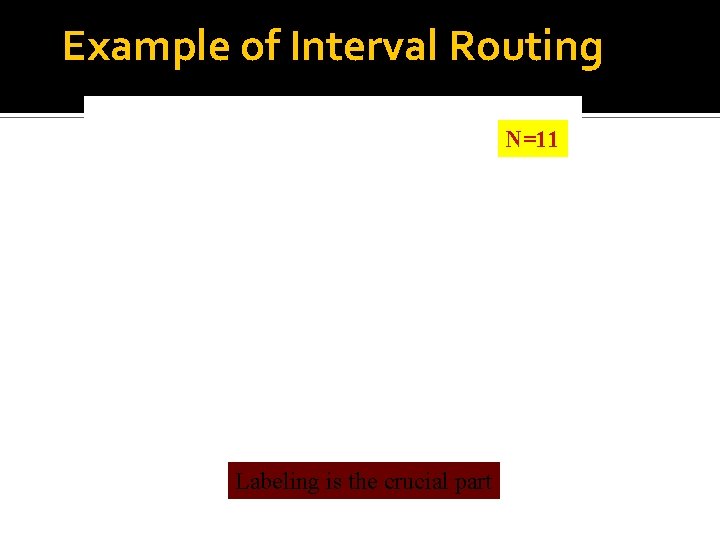
Example of Interval Routing N=11 Labeling is the crucial part

Labeling algorithm Label the root as 0. Do a pre-order traversal of the tree. Label successive nodes as 1, 2, 3 For each node, label the port towards a child by the node number of the child. Then label the port towards the parent by L(i) + T(i) + 1 mod N, where - L(i) is the label of the node i, - T(i) = # of nodes in the subtree under node i (excluding i), Question 1. Why does it work? Question 2. Does it work for non-tree topologies too? YES, but the construction is somewhat tricky.

Another example Interval routing on a ring. The routes are not optimal. To make it optimal, label the ports of node i with i+1 mod 8 and i+4 mod 8.
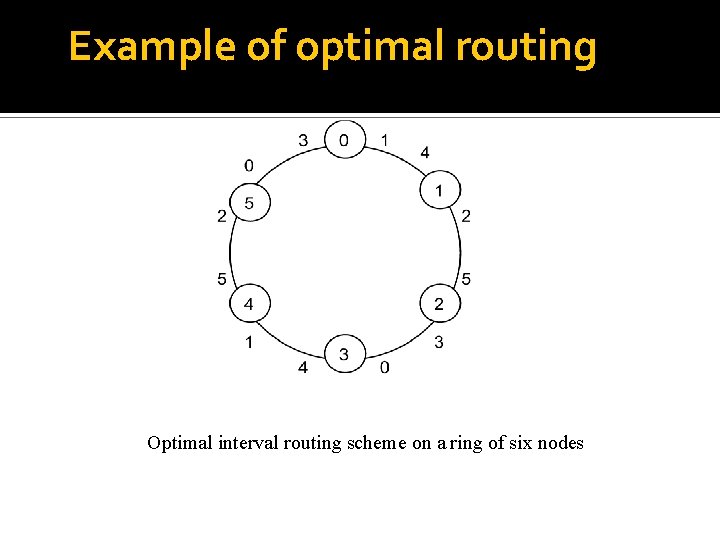
Example of optimal routing Optimal interval routing scheme on a ring of six nodes

So, what is the problem? Works for static topologies. Difficult to adapt to changes in topologies. But there is some recent work on compact routing in dynamic topologies (Amos Korman, ICDCN 2009)
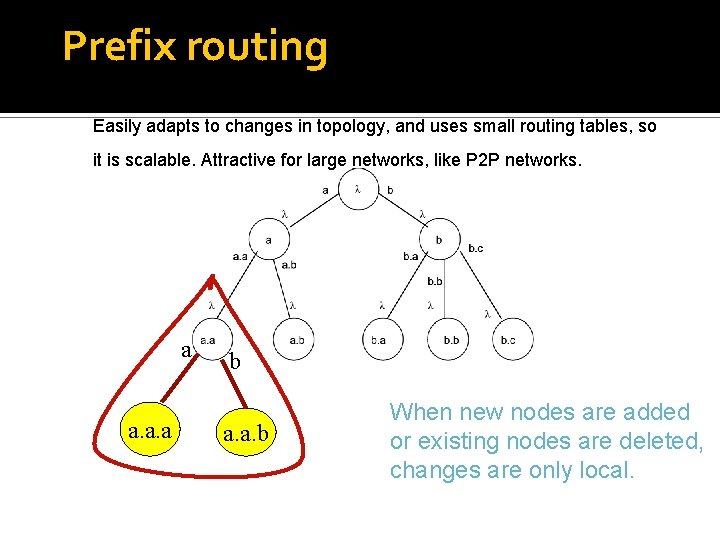
Prefix routing Easily adapts to changes in topology, and uses small routing tables, so it is scalable. Attractive for large networks, like P 2 P networks. a a. a. a b a. a. b When new nodes are added or existing nodes are deleted, changes are only local.
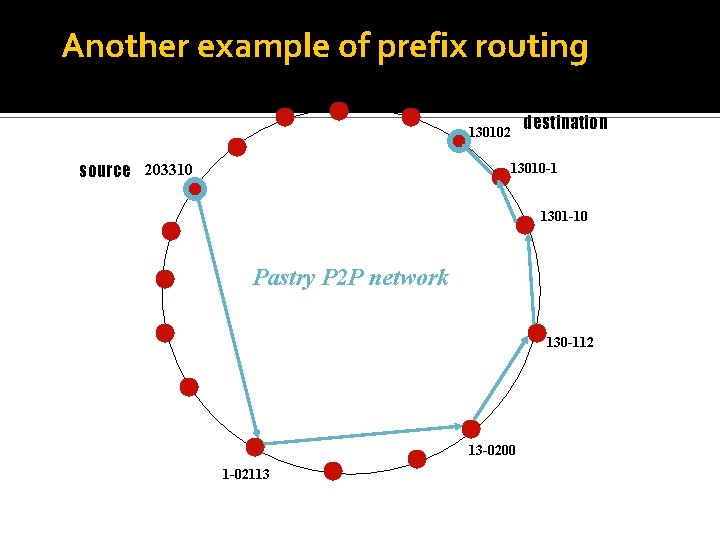
Another example of prefix routing destination 130102 source 203310 13010 -1 1301 -10 Pastry P 2 P network 130 -112 13 -0200 1 -02113
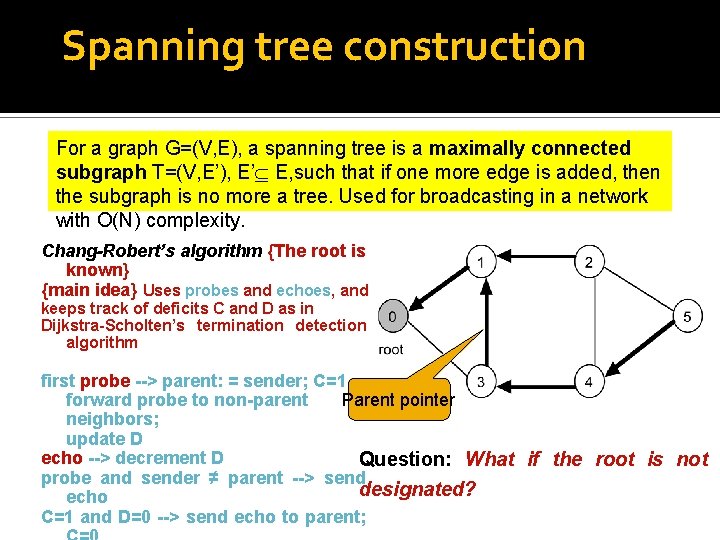
Spanning tree construction For a graph G=(V, E), a spanning tree is a maximally connected subgraph T=(V, E’), E’ E, such that if one more edge is added, then the subgraph is no more a tree. Used for broadcasting in a network with O(N) complexity. Chang-Robert’s algorithm {The root is known} {main idea} Uses probes and echoes, and keeps track of deficits C and D as in Dijkstra-Scholten’s termination detection algorithm first probe --> parent: = sender; C=1 Parent pointer forward probe to non-parent neighbors; update D echo --> decrement D Question: What if the root is not probe and sender ≠ parent --> send designated? echo C=1 and D=0 --> send echo to parent;

Graph traversal Think about web-crawlers, exploration of social networks, planning of graph layouts for visualization or drawing etc. Many applications of exploring an unknown graph by a visitor (a token or mobile agent or a robot). The goal of traversal is to visit every node at least once, and return to the starting point. - How efficiently can this be done? - What is the guarantee that all nodes will be visited? (oris BFS) is well so we will not discuss about it -DFS What the traversal guarantee thatknown, the algorithm terminate?
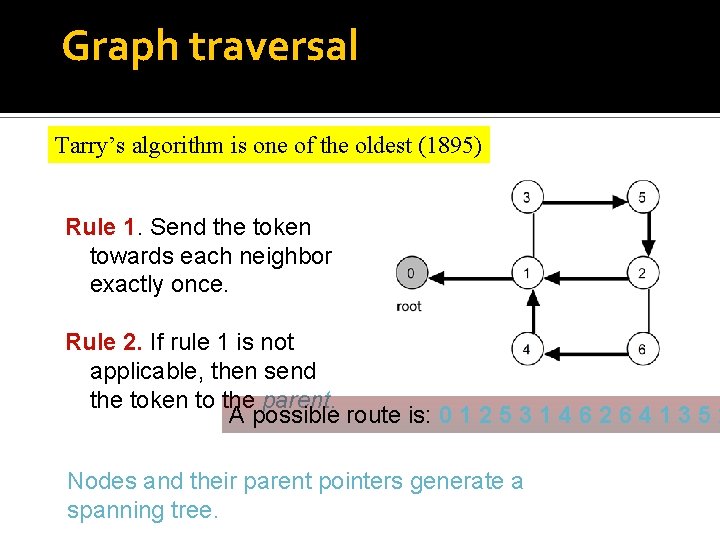
Graph traversal Tarry’s algorithm is one of the oldest (1895) Rule 1. Send the token towards each neighbor exactly once. Rule 2. If rule 1 is not applicable, then send the token to the parent. A possible route is: 0 1 2 5 3 1 4 6 2 6 4 1 3 5 2 Nodes and their parent pointers generate a spanning tree.

Minimum Spanning Tree Given a weighted graph G = (V, E), generate a spanning tree T = (V, E’) E’ E such that the sum of the weights of all the edges is minimum. Applications Minimum cost vehicle routing The traveling salesman problem asks for the shortest route to visit a collection of cities and return to the starting point. On Euclidean plane, approximate solutions to the traveling salesman problem, Lease phone lines to connect the different offices with a minimum cost, Visualizing multidimensional data (how entities are related to each other) We are interested in distributed algorithms only
Example
Sequential algorithms for MST Review (1) Prim’s algorithm and (2) Kruskal’s algorithm. Theorem. If the weight of every edge is distinct, then the MST is unique.

Minimum Spanning Tree Given a weighted graph G = (V, E), generate a spanning tree T = (V, E’) such that the sum of the weights of all the edges is minimum. Applications The traveling salesman problem asks for the shortest route to visit a collection of cities and return to the starting point. On Euclidean plane, approximate solutions to the traveling salesman problem, Lease phone lines to connect the different offices with a minimum cost, Visualizing multidimensional data (how entities are related to each other) We are interested in distributed algorithms only
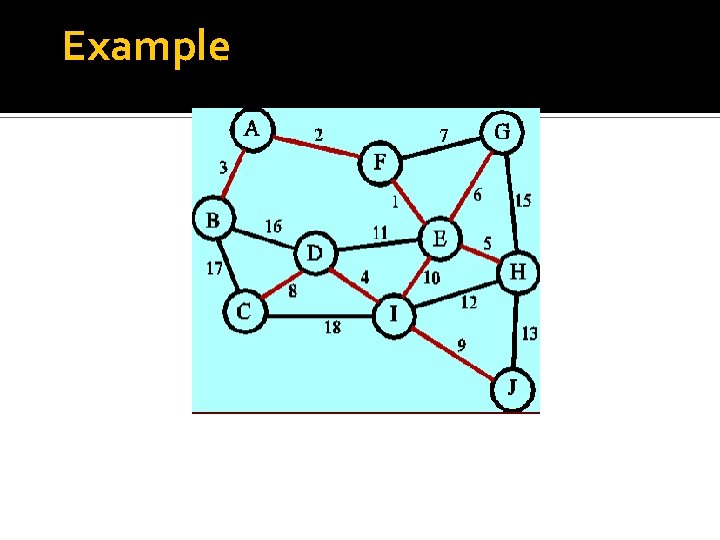
Example
Sequential algorithms for MST Review (1) Prim’s algorithm and (2) Kruskal’s algorithm. Theorem. If the weight of every edge is distinct, then the MST is unique.
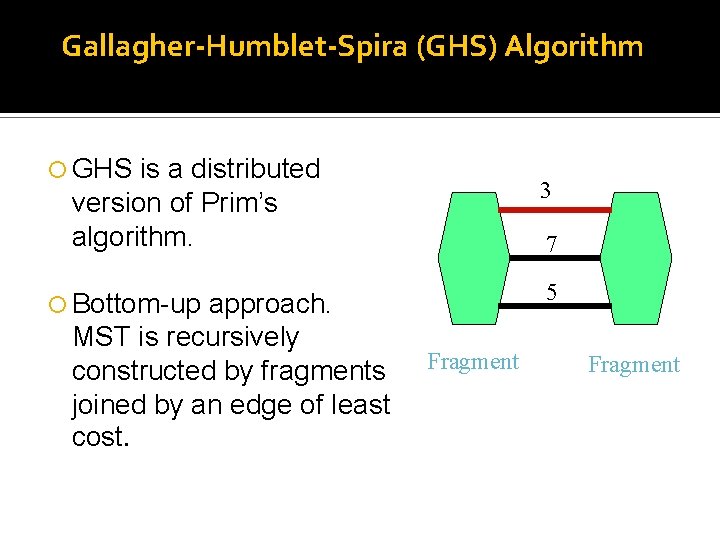
Gallagher-Humblet-Spira (GHS) Algorithm GHS is a distributed version of Prim’s algorithm. approach. MST is recursively constructed by fragments joined by an edge of least cost. 3 7 5 Bottom-up Fragment
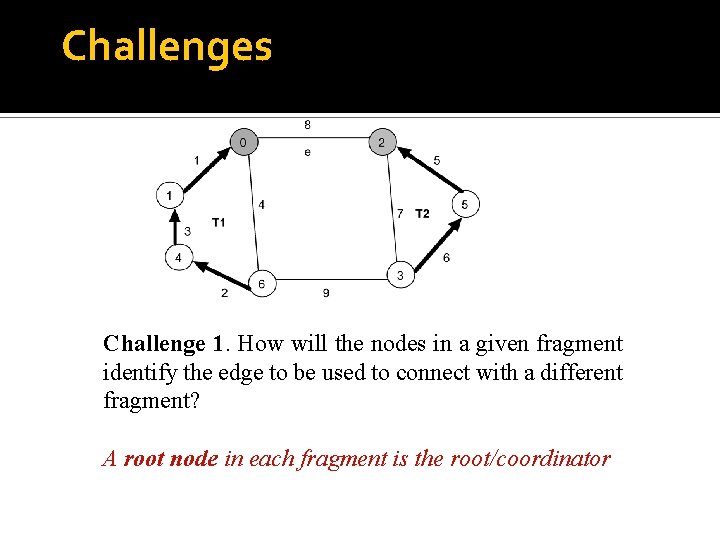
Challenges Challenge 1. How will the nodes in a given fragment identify the edge to be used to connect with a different fragment? A root node in each fragment is the root/coordinator

Challenges Challenge 2. How will a node in T 1 determine if a given edge connects to a node of a different tree T 2 or the same tree T 1? Why will node 0 choose the edge e with weight 8, and not the edge with weight 4? Nodes in a fragment acquire the same name before augmentation.

Two main steps Each fragment has a level. Initially each node is a fragment at level 0. (MERGE) Two fragments at the same level L combine to form a fragment of level L+1 (ABSORB) A fragment at level L is absorbed by another fragment at level L’ (L < L’). The new fragment jhas a level L’. (Each fragment in level L has at least 2 L nodes)
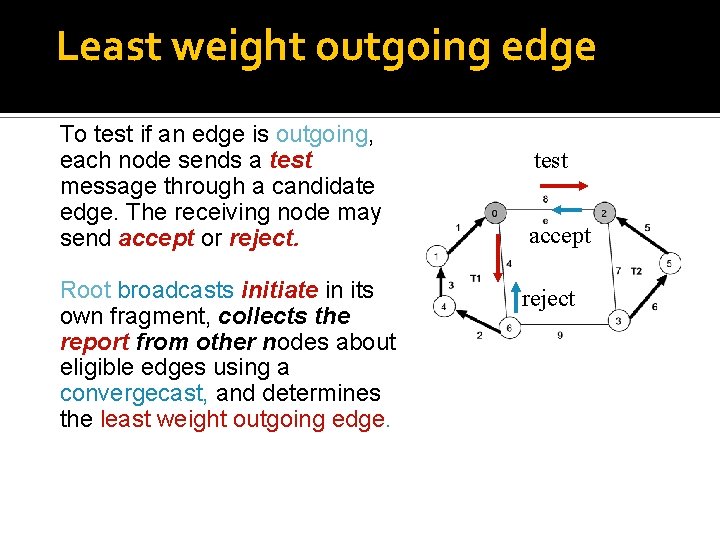
Least weight outgoing edge To test if an edge is outgoing, each node sends a test message through a candidate edge. The receiving node may send accept or reject. Root broadcasts initiate in its own fragment, collects the report from other nodes about eligible edges using a convergecast, and determines the least weight outgoing edge. test accept reject
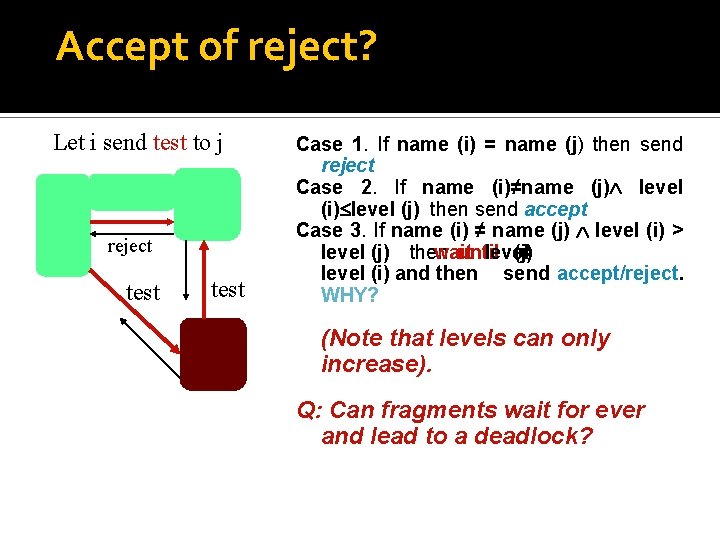
Accept of reject? Let i send test to j reject test Case 1. If name (i) = name (j) then send reject Case 2. If name (i)≠name (j) level (i) level (j) then send accept Case 3. If name (i) ≠ name (j) level (i) > level (j) then wait until level (j) = level (i) and then send accept/reject. WHY? (Note that levels can only increase). Q: Can fragments wait for ever and lead to a deadlock?

The major steps repeat 1 Test edges as outgoing or not 2 Determine lwoe - it becomes a tree edge 3 Send join (or respond to join) 4 Update level & name & identify new coordinator/root until done

Classification of edges Basic (initially all branches are basic) Branch (all tree edges) Rejected (not a tree edge) Branch and rejected are stable attributes
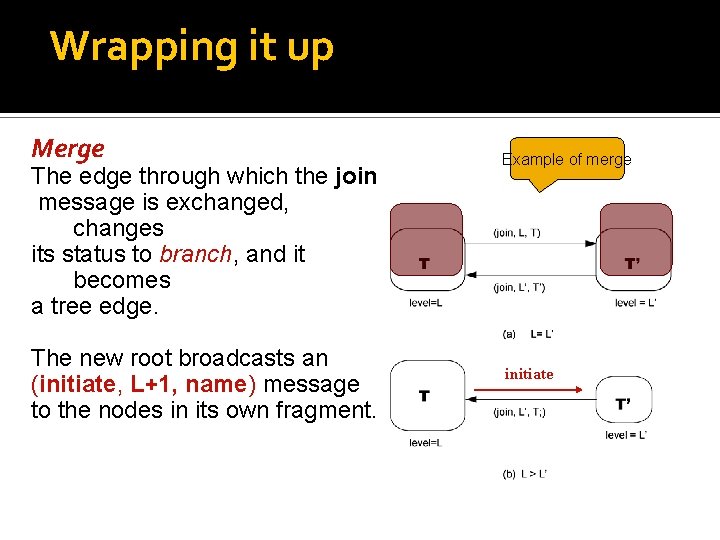
Wrapping it up Merge The edge through which the join message is exchanged, changes its status to branch, and it becomes a tree edge. The new root broadcasts an (initiate, L+1, name) message to the nodes in its own fragment. Example of merge initiate
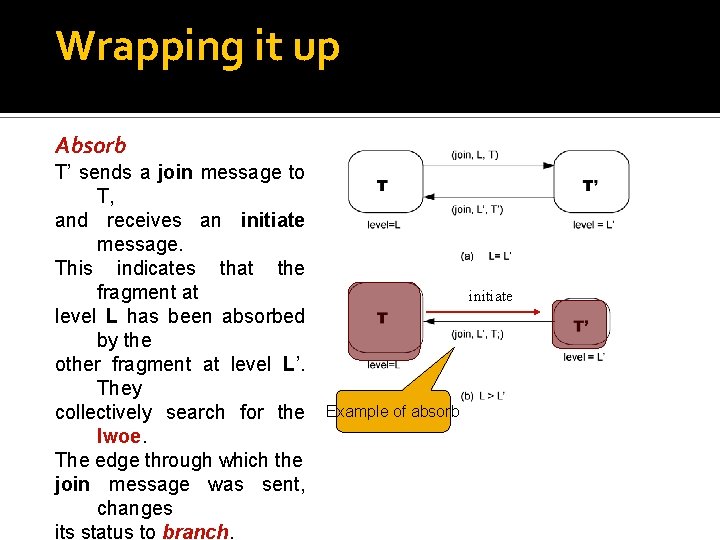
Wrapping it up Absorb T’ sends a join message to T, and receives an initiate message. This indicates that the fragment at level L has been absorbed by the other fragment at level L’. They collectively search for the lwoe. The edge through which the join message was sent, changes its status to branch. initiate Example of absorb
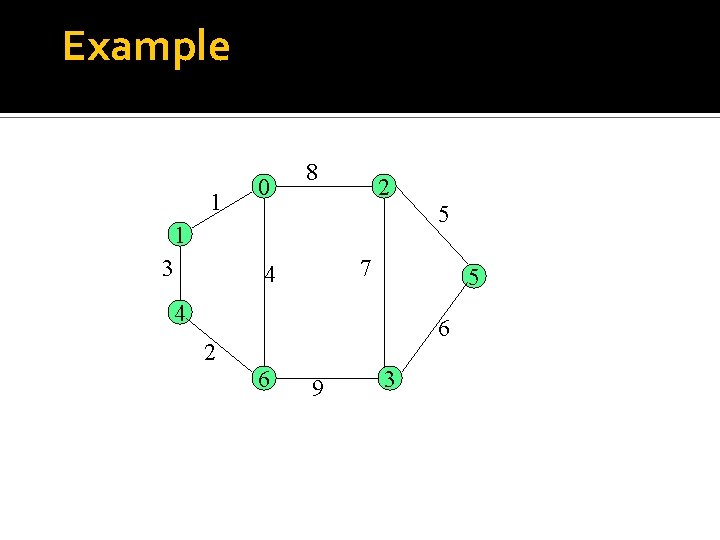
Example 1 0 8 2 5 1 3 7 4 5 4 6 2 6 9 3
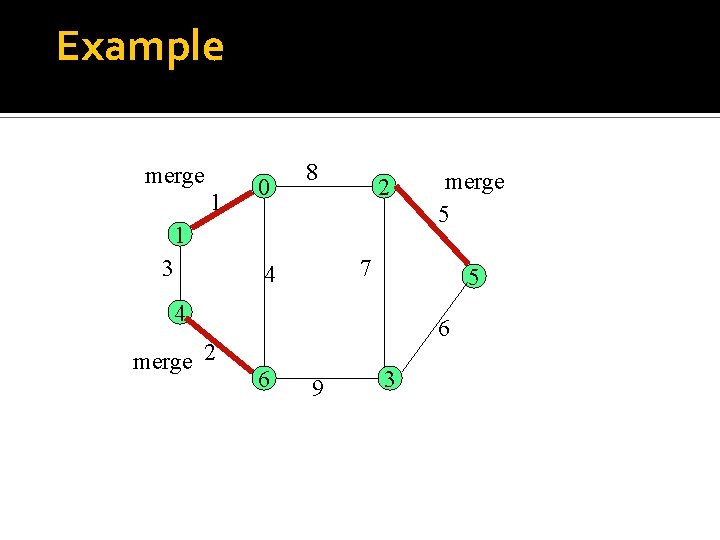
Example merge 1 0 8 2 1 3 7 4 5 4 merge 2 merge 5 6 6 9 3
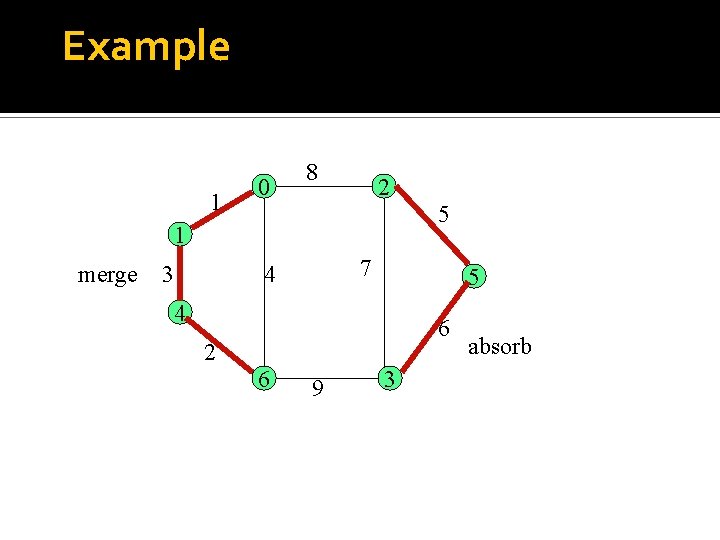
Example 1 0 8 2 5 1 merge 3 7 4 5 4 6 2 6 9 3 absorb
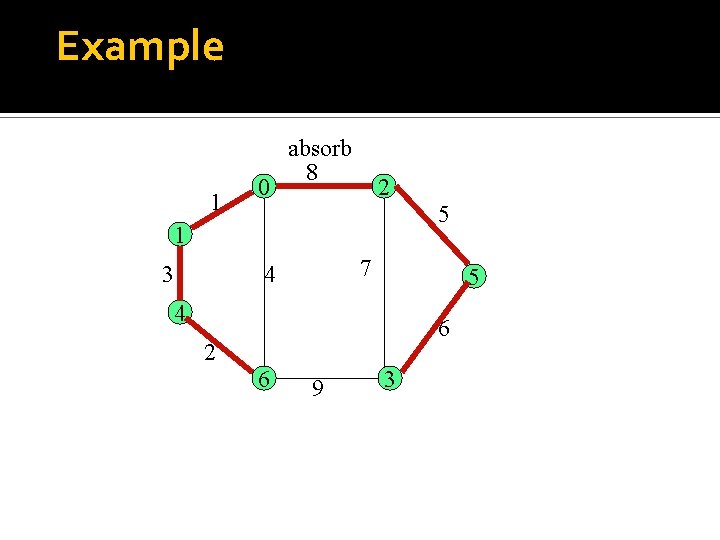
Example 1 0 absorb 8 2 5 1 3 7 4 5 4 6 2 6 9 3

Message complexity At least two messages (test + reject) must pass through eac rejected edge. The upper bound is 2|E| messages. At each of the log N levels, a node can receive at most (1) o initiate message and (2) one accept message (3) one join message (4) one test message not leading to a rejection, a (5) one changeroot message. So, the total number of messages has an upper bound of 2|E| + 5 N log. N
- Slides: 47