Hvorfor er det svrt at lre matematik differentialregning

Hvorfor er det svært at lære matematik? - differentialregning som eksempel Morten Blomhøj, IMFUFA Roskilde Universitetscenter 1. En scene fra matematikundervisningens praksis 2. Matematiske begrebers forhold til virkeligheden 3. Matematiske begreber og deres repræsentationer 4. En model for dannelse af matematiske begreber 5. Hvad er viden? – en netværksmetafor 6. Følelsesmæssige sider af matematiklæring

En scene fra matematikundervisningen - differentialkvotienten til f(x)=x 2 L: Først danner vi differenskvotienten. (Læreren skriver på tavlen) L: Og så reducerer vi.

L: Nu kan vi lade x går mod x 0. Og så går differenskvotienten mod differentialkvotienten. Vi får: for L: Differentialkvotient for x 2 er altså 2 x 0 i x 0. Og da vi kan vælge x 0 frit betyder det, at differentialkvotienten til x 2 over alt er 2 x. Det skriver vi sådan: eller for alle x E: Jeg forstår ikke, hvordan du kom frem til x 0 + x 0 L: Forstår du ikke, at faktoren (x- x 0) kan forkortes ud i denne brøk (læreren peger på brøken på tavlen)?

E: Jo, men hvordan kom du frem til den brøk? L: Forskellen på to tals kvadrater er produktet af tallenes differens og tallenes sum. Læreren regner på tavlen: E: Ja, men det var jo x 2 - xo 2 du havde! L: Ja, og hvad så? E: Hvordan fandt du på det? - jeg ville aldrig kunne have gjort det selv!

E: Jeg forstår ikke det med x 0 - hvad er x 0 egentlig? L: x 0 er et vilkårligt valgt fast tal. E: Jamen, hvad er x så? L: x kan vi varierer frit på, når vi lader x gå mod x 0 kan vi skifte ud med et vilkårligt tal f. eks. 3. Hvis du gør det hele vejen gennem beviset får du: E: Hvorfor skriver du så til sidst? L: Det er fordi vi kan vælge x 0 helt frit. Det bevis her gælder for alle mulige værdier af x 0, og derfor skriver vi bare: E: Vil det sige, at x 0 = x? …….

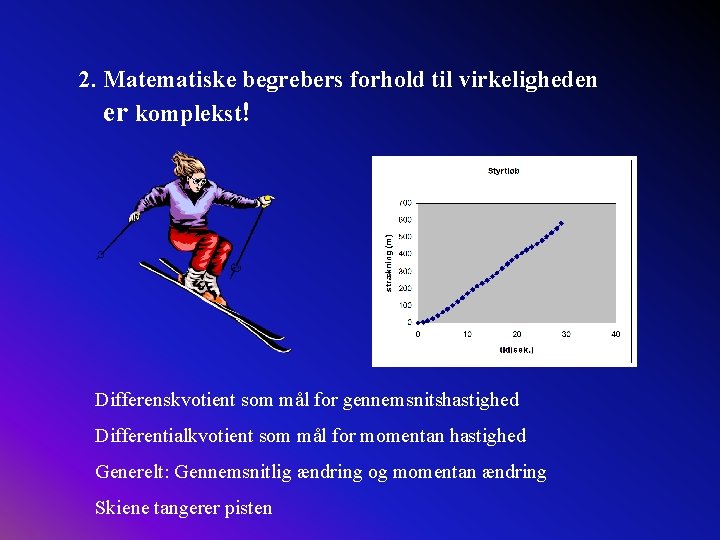
2. Matematiske begrebers forhold til virkeligheden er komplekst! Differenskvotient som mål for gennemsnitshastighed Differentialkvotient som mål for momentan hastighed Generelt: Gennemsnitlig ændring og momentan ændring Skiene tangerer pisten

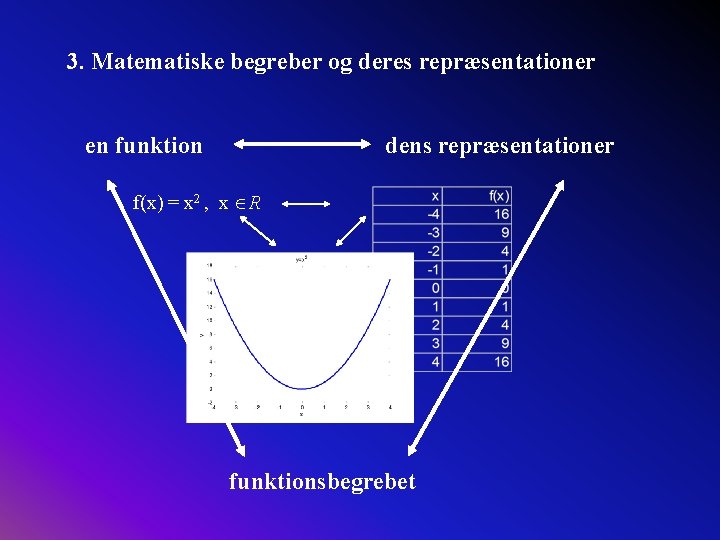
3. Matematiske begreber og deres repræsentationer en funktion dens repræsentationer f(x) = x 2 , x R funktionsbegrebet

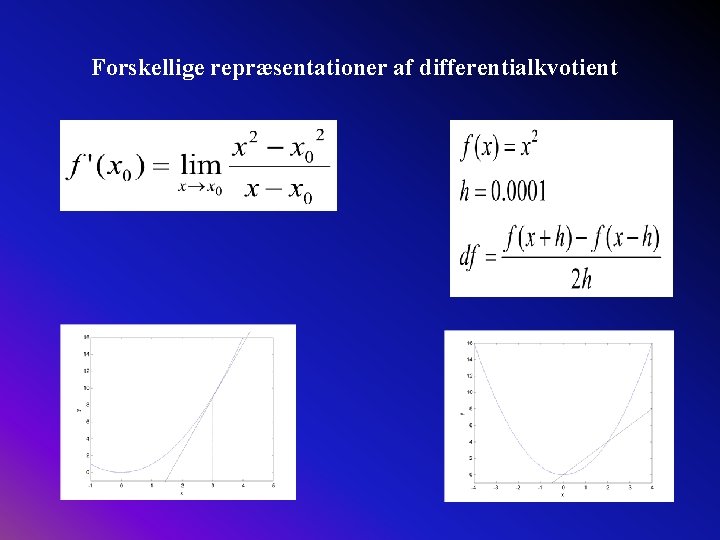
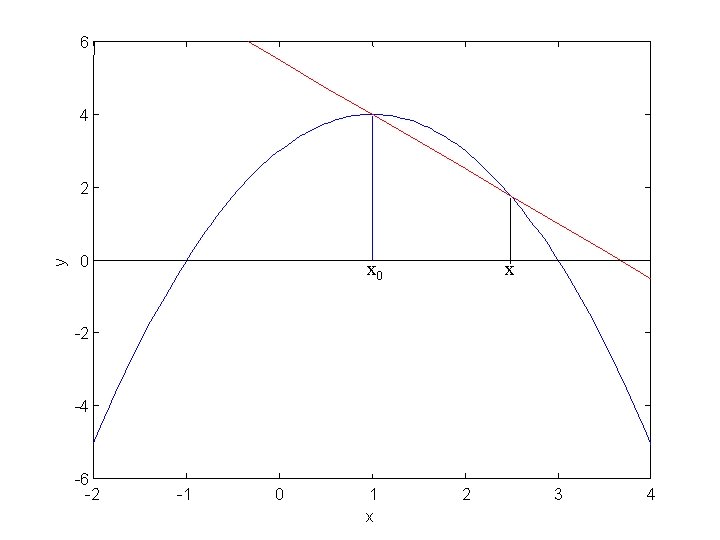
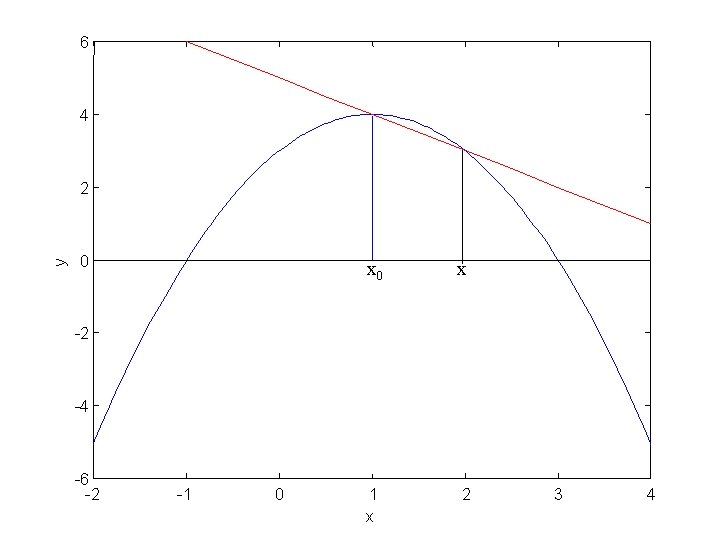
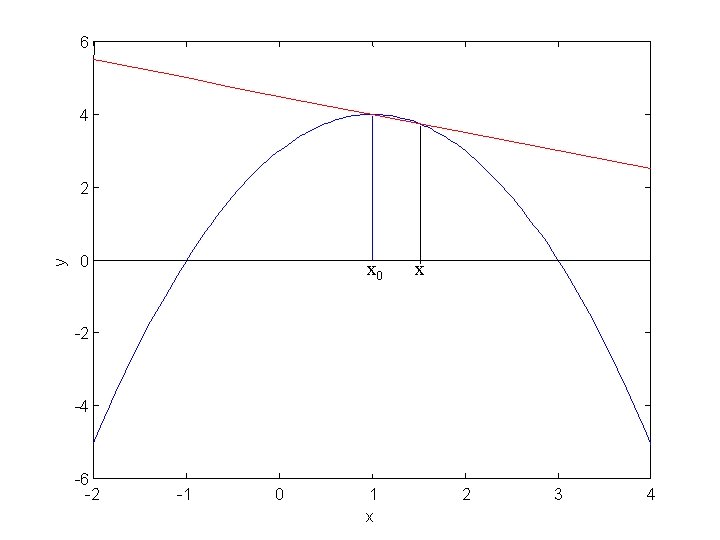
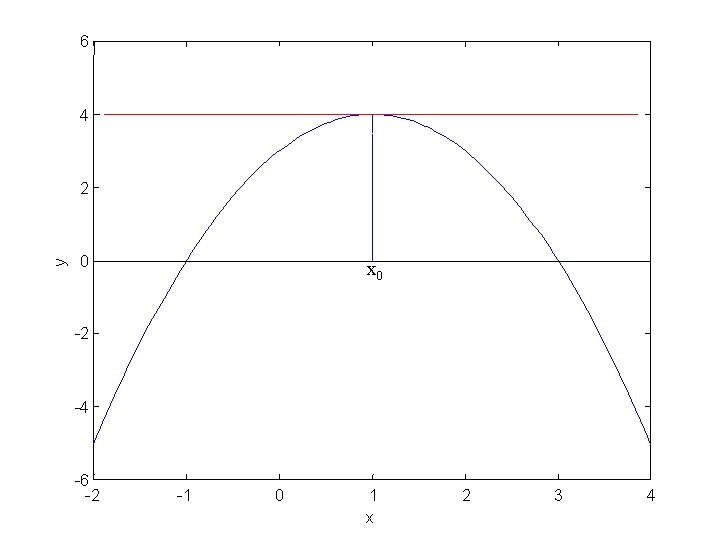
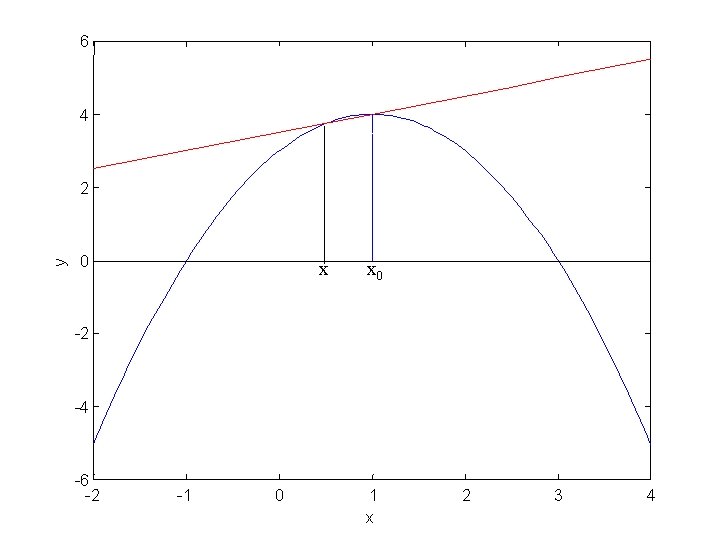
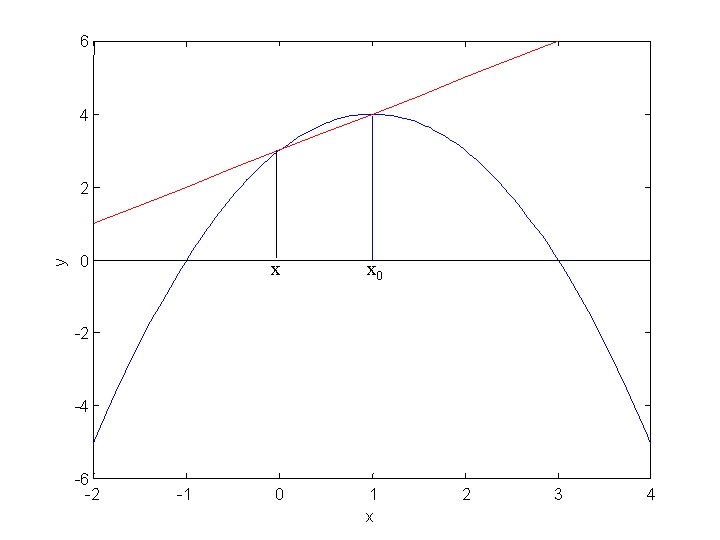
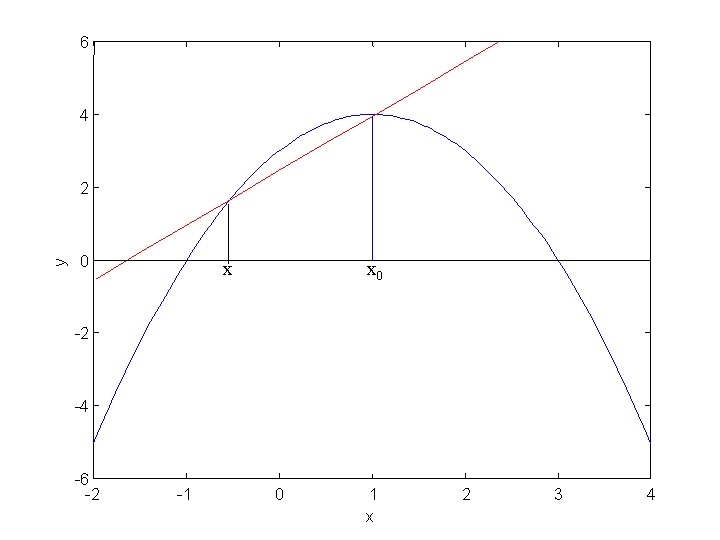
Forskellige repræsentationer af differentialkvotient

6 4 y 2 0 x -2 -4 -6 -2 -1 0 1 x 2 3 4

6 4 y 2 0 x 1 x 2 -2 -4 -6 -2 -1 0 3 4

6 4 y 2 0 x -2 -4 -6 -2 -1 0 1 x 2 3 4

6 4 y 2 0 x 0 -2 -4 -6 -2 -1 0 1 x 2 3 4

6 4 y 2 0 x x 0 -2 -4 -6 -2 -1 0 1 x 2 3 4

6 4 y 2 0 x x 0 0 1 x -2 -4 -6 -2 -1 2 3 4

6 4 y 2 0 x x 0 -2 -4 -6 -2 -1 0 1 x 2 3 4

4. En model for dannelse af matematiske begreber A) Procesforståelse går forud for objektforståelse. B) Begrebsdannelsensprocessen har en hierarkisk struktur med tre faser: C) internalisering, kondensering og tingsliggørelse. C) Samspil mellem at opfatte et begreb som en proces og et selvstændigt objekter er afgørende i matematiklæring. (Anna Sfard, 1991)

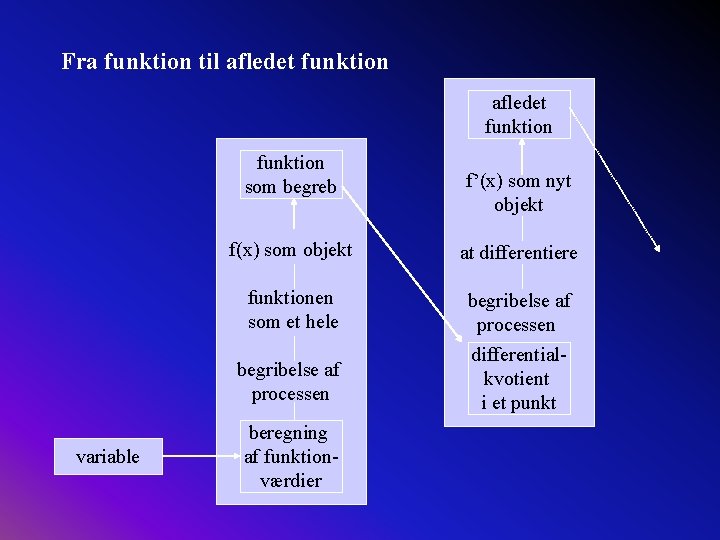
Fra funktion til afledet funktion som begreb variable f’(x) som nyt objekt f(x) som objekt at differentiere funktionen som et hele begribelse af processen differentialkvotient i et punkt beregning af funktionværdier

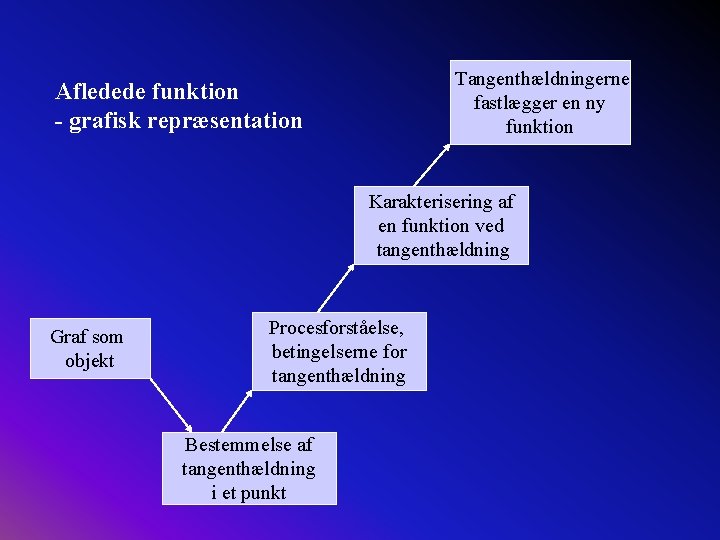
Tangenthældningerne fastlægger en ny funktion Afledede funktion - grafisk repræsentation Karakterisering af en funktion ved tangenthældning Graf som objekt Procesforståelse, betingelserne for tangenthældning Bestemmelse af tangenthældning i et punkt

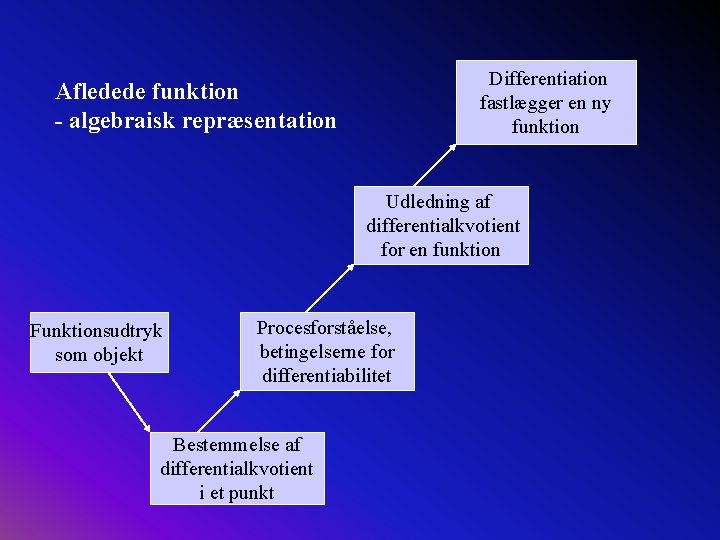
Differentiation fastlægger en ny funktion Afledede funktion - algebraisk repræsentation Udledning af differentialkvotient for en funktion Funktionsudtryk som objekt Procesforståelse, betingelserne for differentiabilitet Bestemmelse af differentialkvotient i et punkt

Principielle vanskeligheder ved differentialregning • Differentiation forudsætter forståelse af funktionsbegrebet. • Grænseværdi er kognitivt set et svært begreb. • Differentiation er defineret punktvis (lokalt), men anvendes globalt. • Forståelse kræver skift mellem algebraiske, geometriske og numeriske beskrivelsesformer. • Differentiation har ofte høj algebraisk kompleksitet.

Regneregler for differentiation En konstant kan ”sættes uden for” differentiation: Hvert led differentieres for sig: Produktreglen:

Differentiation af en brøk af funktioner Differentiation af sammensat funktioner (kædereglen):

Nogle vigtige funktioner og deres afledede funktioner

5. Hvad er viden? – en netværksmetafor

Begrebskort for differentialkvotient Stedfunktionen Funktionsgraf Funktions- forskrift Differentiabilitet Sekant Gennemsnitshastighed Differential- kvotient Differentialligning Afledet funktion Tangent Momentanhastighed Vækstmodeller Differenskvotient Regneregler for diff. Hastighedsfunktion

6. Følelsesmæssige sider af matematiklæring • Det kan være svært at se en personlig mening med matematik. • Det opleves meget tydeligt, når der er noget man ikke forstår. • Det er svært at kommunikere om det man ikke forstår. • Ny forståelse og erkendelse opleves som personlig succes og mangel på samme som personlig fiasko. • At være god til matematik opleves som et enten eller. • Matematikfaget har en sorterende og disciplinerende rolle i uddannelsessystemet.

Referencer Arcavi, A. , 1994: Symbol sense: Informal sense-making in formal mathematics. For the Learning of Mathematics, 14, 3 (Nov. ), 24 -35. Blomhøj, M. , 1997: Funktionsbegrebet og 9. klasse elevers begrebsforståelse. Nordisk Matematikk. Didaktikk, nr. 1, juni 1997, 7 -29. Blomhøj, M. , 1995: Den didaktiske kontrakt i matematikundervisningen. Nämnaren, 4. årg. nr. 3, 16 -25. Dubinsky, E. & M. A. Mcdonald (2001): APOS: A constructivist theory of learning in undergraduate mathematics education research. I Holton, D. (Ed. ): The teaching and learning of mathematics at university level: An ICMI-study, 275 -282, Dordrecht, Kluwer. Brousseau, G. , 1997: Theory of didactical situations in mathematics. Dordrecht, Kluwer. Sfard, A. , 1991. On the dual nature of mathematical conceptions: Reflections on processes and objects as different sides of the same coin. Educational Studies in Mathematics, 22, 1 -36. Stienbring, H. , 1987: Routine and meaning in the mathematics classroom. For the Learning of Mathematics, 9, nr. 1, 24 -33. Skovsmose, O. & M. Blomhøj (red. ), 2003: Kan det virkelig passe? om matematiklæring. København, L&R Uddannelse.

Tall, D. , 1996: Functions and Calculus. I International handbook of mathematics education, A. J. Bishop et al. (eds. ), 289 -325, Dordrecht, Kluwer. Tall, D. , 1992: The transition to advanced mathematical thinking: functions, limits, infinity, and proof. I Handbook of research on mathematical teaching and learning. D. A. Grows (ed. ), NCTM, Macmillan Publ. co. USA. Tall, D. & Vinner, S. , 1981: Concept image and concept definition in mathematics, with particular reference to limits and continuity. Educational Studies in Mathematics, 12, 151169. Vinner, S. & T. Dreyfus, 1989: Images and definitions of the concept of function. Journal for Research in Mathematics Education, 20, 356 -366.

Nogle opgaver til at tage med hjem 1. Om en funktion f(x) vides at f(-x) = f(x) for alle x, og at f’(2)=2. Hvad er f’(-2)? 2. Lav en forskrift for en funktion, der har sin egen afledet som tangent i punktet (1, f(1)). 3. En differentiabel funktion har følgende funktionstabel Skitser grafen for den afledede funktion.