Human Variability and Statistics Dealing with Human Situational

Human Variability and Statistics Dealing with Human, Situational and Temporal Variability Brian Peacock for Pitney Bowes Inc © Brian Peacock Ergonomics (BPE) Pte. Ltd.

People Vary © Brian Peacock Ergonomics (BPE) Pte. Ltd. on many dimensions – name some

Situations and effects of Time vary �Type of machine or tool �Time of day, year �Lighting �Fatigue �Task �Age �Materials �Learning, experience �Location �etc © Brian Peacock Ergonomics (BPE) Pte. Ltd. �Length of job cycle �etc

Types of Data �Qualitative �Nominal - Different from, group, class �Sex, ethnicity, house location �Ordinal (Rank) - Greater (lesser) than �Age order of children, level in military, opinion about products �Quantitative �Equal interval - equal differences �Temperature, sound level �Ratio �Height, Weight, Speed, Salary etc © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Samples and Populations �We use samples to make inferences (generalizations)about populations �Sometimes our samples are biased �We often use Random Sampling �Sometimes our samples are too small �Sometimes our samples are too large and costly �Data cost $$$$ �Mostly we take what we can get and hope for the best (and use statistics to guard against unreliable conclusions) © Brian Peacock Ergonomics (BPE) Pte. Ltd.

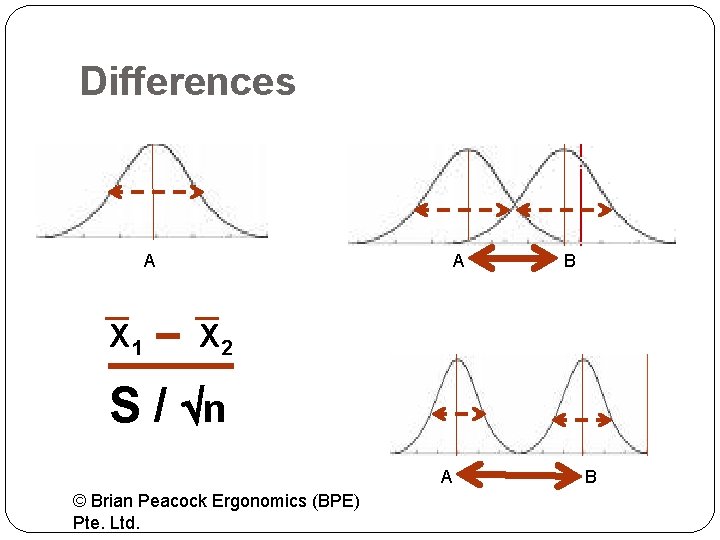
Differences A X 1 A B X 2 S / n A © Brian Peacock Ergonomics (BPE) Pte. Ltd. B

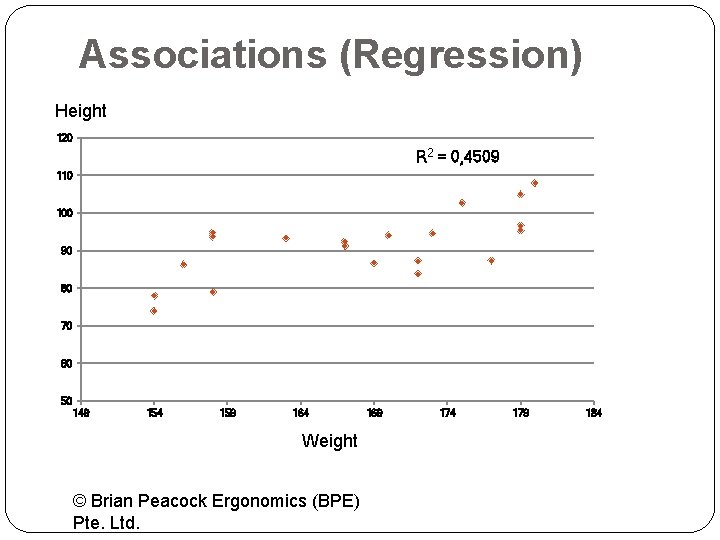
Associations (Regression) Height 120 R 2 = 0, 4509 110 100 90 80 70 60 50 149 154 159 164 Weight © Brian Peacock Ergonomics (BPE) Pte. Ltd. 169 174 179 184

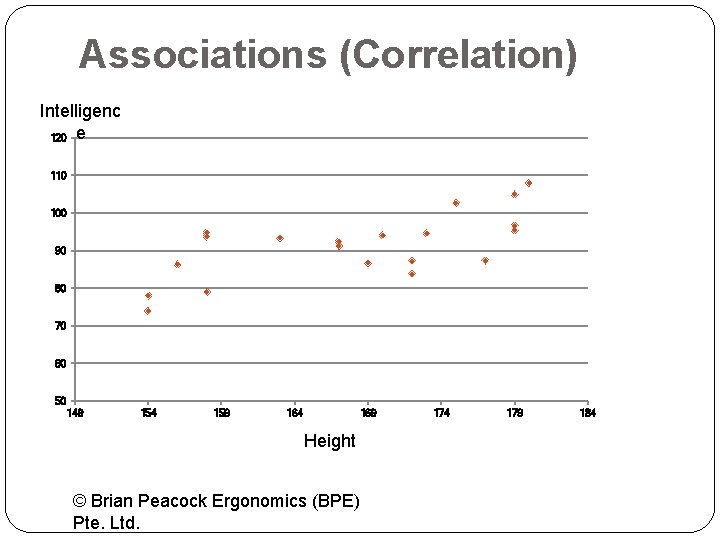
Associations (Correlation) Intelligenc 120 e 110 100 90 80 70 60 50 149 154 159 164 169 Height © Brian Peacock Ergonomics (BPE) Pte. Ltd. 174 179 184

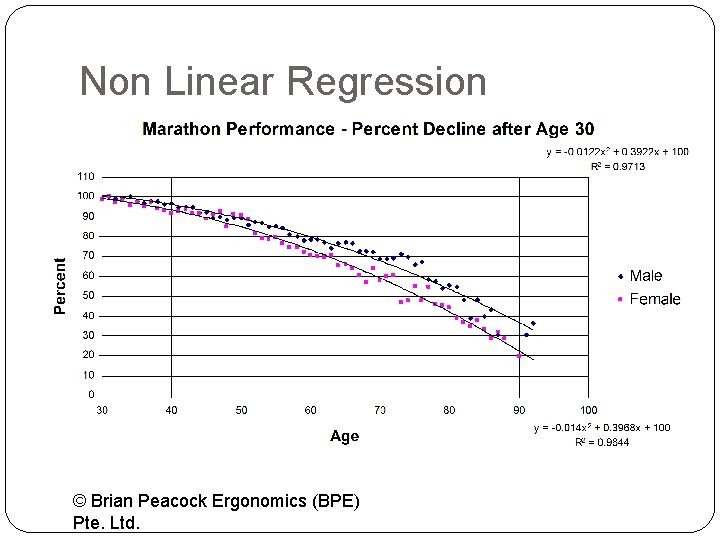
Non Linear Regression © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Policy, percentiles and other statistics exercises © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Data Capture 1. 2. 3. 4. 5. 6. 7. Clear a space in the classroom Arrange yourselves in a row with the shortest to the left and the tallest to the right. a) It’s easier if you split into groups of 10 Counting from the left, show that the person with the 10 th percentile stature is the one with nearest integer to n/10 Similarly the 90 th percentile is the one with the nearest integer to n*9/10 The class member with the average (median) height is the one with the nearest integer to n/2 Find the 5 th and 95 th percentiles How does sample size affect the results? © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Weight 1. Have each member of the class recall his / her weight (kg) 2. Divide this score by 10 and have the class member move forward that number of paces 3. Stretch a long piece of string through the group of people so that there an equal number of class members on each side of the string and in each quadrant formed by the string and the median height. 4. This is the linear regression line that shows the relationship between stature and height 5. Calculate the 10 th and 90 th percentiles and the median for weight © Brian Peacock Ergonomics (BPE) Pte. Ltd.

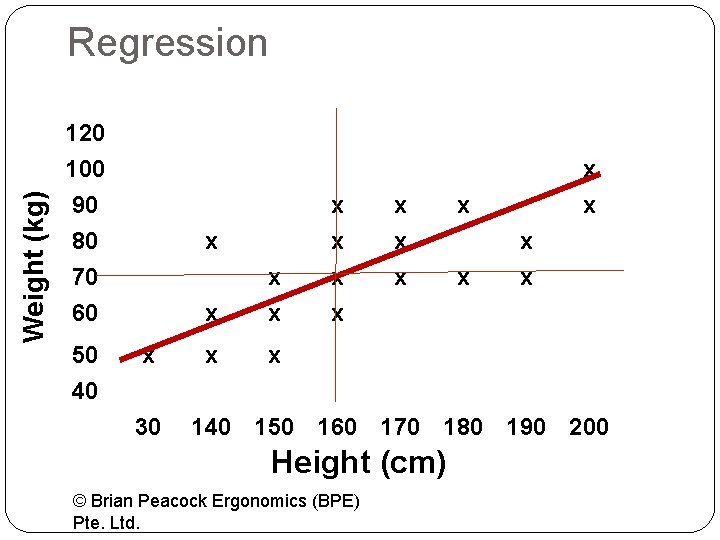
Weight (kg) Regression 120 100 90 80 x 70 60 50 40 x 30 x x x x x 140 150 160 170 180 190 200 Height (cm) © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Conclusions �These simple anthropometric measurements are the basis of workplace design. �The same exercise can be carried out for other body segment lengths, widths and girths �Similar statistical techniques are used in workplace design �More elaborate anthropometric techniques use full body scanning �The same approach can be used for other human characteristics and performance capabilities �Running, typing, seeing, assembling, carrying, welding, calculating and so on © Brian Peacock Ergonomics (BPE) Pte. Ltd.

© Brian Peacock Ergonomics (BPE) Pte. Ltd. The Policy Question � Traditionally we accommodate the 5 th percentile for reach and the 95 th percentile for fit with anthropometric measures. � Are these policies reasonable? � Are these policies reasonable for other human characteristics and performance capabilities? � What situations would make you argue to change these policies? � What is “experienced worker time standard? ” A B C © Brian Peacock Ergonomics (BPE) Pte. Ltd. Time

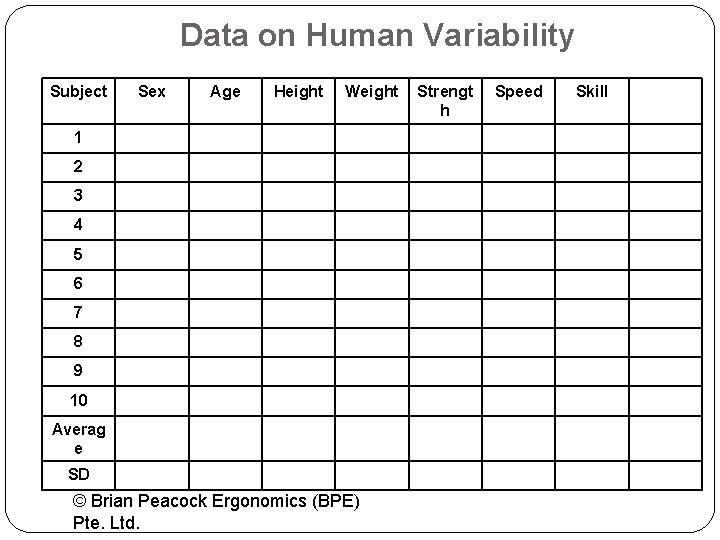
Data on Human Variability Subject Sex Age Height Weight 1 2 3 4 5 6 7 8 9 10 Averag e SD © Brian Peacock Ergonomics (BPE) Pte. Ltd. Strengt h Speed Skill

Experimental Design Brian Peacock © Brian Peacock Ergonomics (BPE) Pte. Ltd.

The Purposes of Experimental Design �To explore (control) the effects of the independent variables and their interactions on the dependent variables �To account for concomitant (uncontrollable) effects (Variables in which you are not interested, but which might affect the outcome) �To economize in the use of data - often data points are expensive in time / money �To avoid confounding between separate variables © Brian Peacock Ergonomics (BPE) Pte. Ltd.

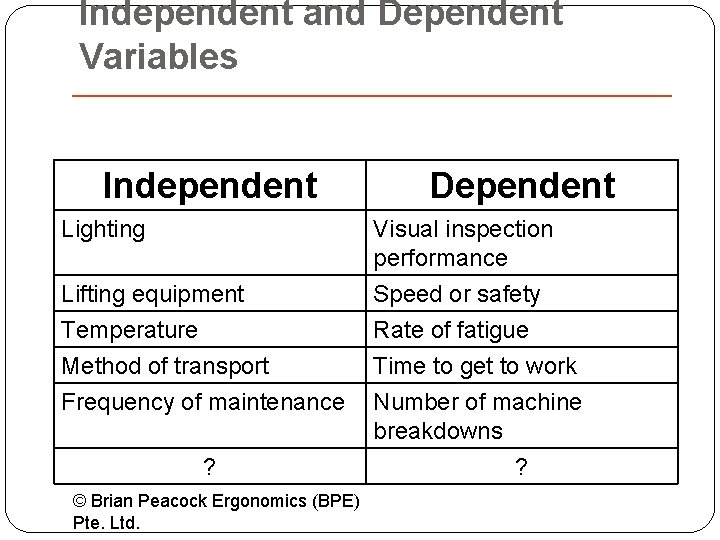
Independent and Dependent Variables Independent Lighting Lifting equipment Temperature Method of transport Frequency of maintenance ? © Brian Peacock Ergonomics (BPE) Pte. Ltd. Dependent Visual inspection performance Speed or safety Rate of fatigue Time to get to work Number of machine breakdowns ?

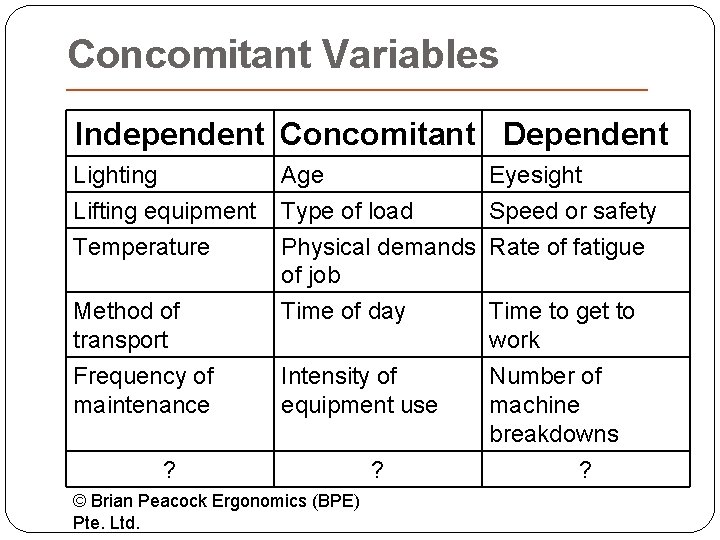
Concomitant Variables Independent Concomitant Dependent Lighting Lifting equipment Temperature Age Eyesight Type of load Speed or safety Physical demands Rate of fatigue of job Method of transport Frequency of maintenance Time of day Intensity of equipment use ? © Brian Peacock Ergonomics (BPE) Pte. Ltd. ? Time to get to work Number of machine breakdowns ?

Confounding § A design that does not distinguish between the causal factors • A study of the effect of number of exits in an airplane on evacuation time using young people for the two exits condition and old people for the four exits condition • Studying two methods of manual materials handling – one in a hot outside environment and one in an air conditioned area © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Data Economy �Experiments on the International Space Station �It cost a lot of $$ to get the equipment up there and there are only a few subjects available to take part in the experiment. � A solution is to study many variables at once using a factorial design using the same subjects for multiple conditions � Airplane evacuation study �Number of doors, number of people, width of aisle �Within and between subjects design © Brian Peacock Ergonomics (BPE) Pte. Ltd.

The Problem • You have a mountain and a river, between the two there is a large field that will be sown to test different kinds of seed and different kinds of fertilizer • How should the plots be arranged? © Brian Peacock Ergonomics (BPE) Pte. Ltd.

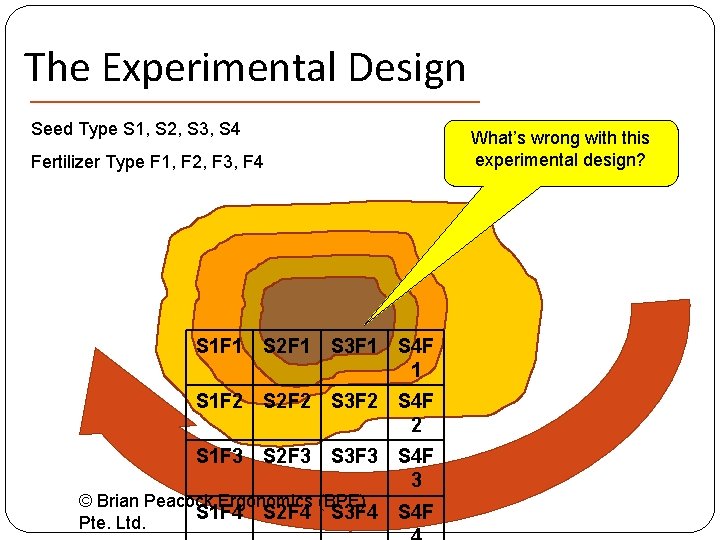
The Experimental Design Seed Type S 1, S 2, S 3, S 4 What’s wrong with this experimental design? Fertilizer Type F 1, F 2, F 3, F 4 S 1 F 1 S 2 F 1 S 3 F 1 S 4 F 1 S 1 F 2 S 2 F 2 S 3 F 2 S 4 F 2 S 1 F 3 S 2 F 3 S 3 F 3 S 4 F 3 © Brian Peacock Ergonomics (BPE) S 1 F 4 S 2 F 4 S 3 F 4 Pte. Ltd. S 4 F

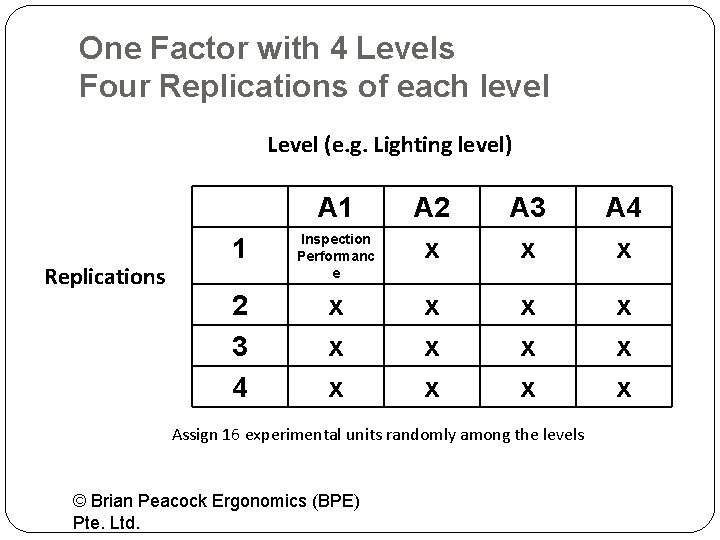
One Factor with 4 Levels Four Replications of each level Level (e. g. Lighting level) A 1 Replications 1 Inspection Performanc e 2 3 4 x x x A 2 x A 3 x A 4 x x x x x Assign 16 experimental units randomly among the levels © Brian Peacock Ergonomics (BPE) Pte. Ltd.

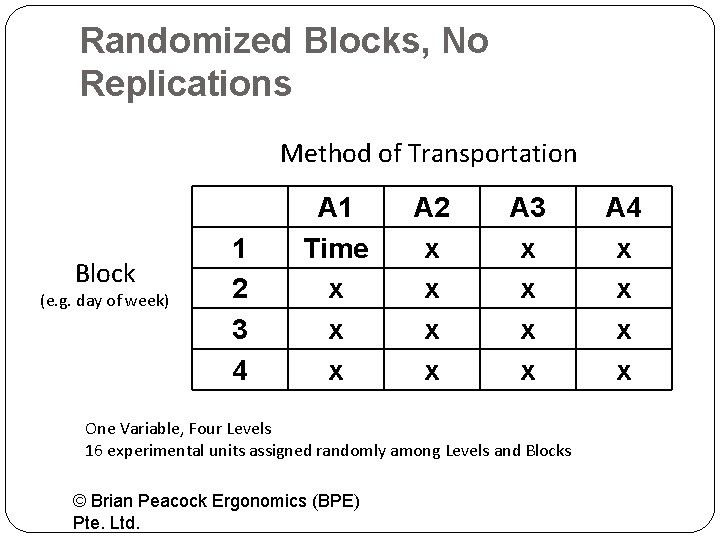
Randomized Blocks, No Replications Method of Transportation Block (e. g. day of week) 1 2 3 4 A 1 Time x x x A 2 x x A 3 x x One Variable, Four Levels 16 experimental units assigned randomly among Levels and Blocks © Brian Peacock Ergonomics (BPE) Pte. Ltd. A 4 x x

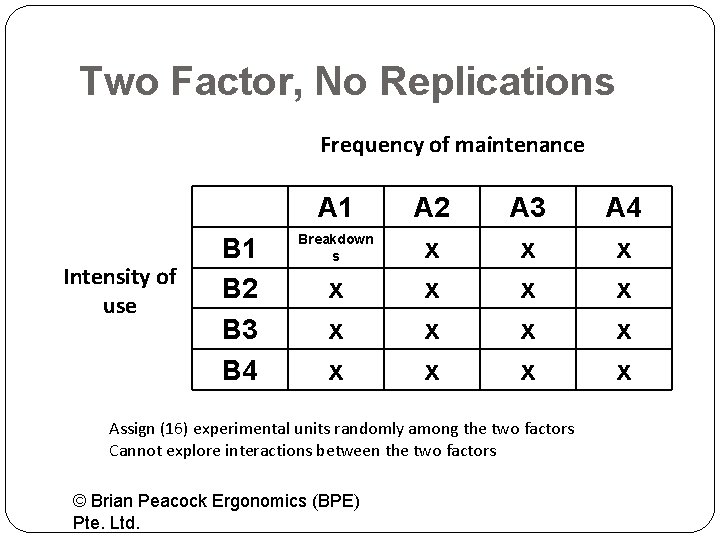
Two Factor, No Replications Frequency of maintenance A 1 Intensity of use B 1 B 2 B 3 B 4 Breakdown s x x x A 2 x x A 3 x x Assign (16) experimental units randomly among the two factors Cannot explore interactions between the two factors © Brian Peacock Ergonomics (BPE) Pte. Ltd. A 4 x x

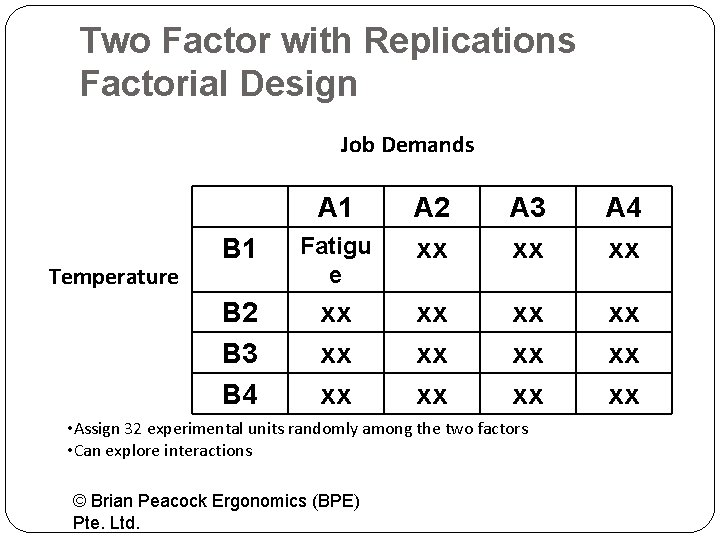
Two Factor with Replications Factorial Design Job Demands A 1 Temperature B 1 Fatigu e B 2 B 3 B 4 xx xx xx A 2 xx A 3 xx A 4 xx xx xx • Assign 32 experimental units randomly among the two factors • Can explore interactions © Brian Peacock Ergonomics (BPE) Pte. Ltd.

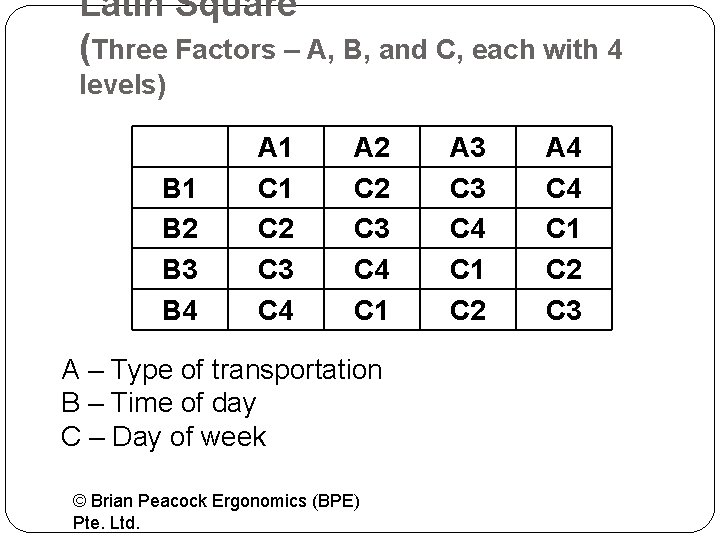
Latin Square (Three Factors – A, B, and C, each with 4 levels) B 1 B 2 B 3 B 4 A 1 C 2 C 3 C 4 A 2 C 3 C 4 C 1 A – Type of transportation B – Time of day C – Day of week © Brian Peacock Ergonomics (BPE) Pte. Ltd. A 3 C 4 C 1 C 2 A 4 C 1 C 2 C 3

Airplane Evacuation Experimental Design �Independent Variable �Number of available doors – 1, 2, 3, 4 �Concomitant variables �Number of passengers – 50, 100, 150, 200 �Dependent Variables �Time to exit �Assumptions �Same model airplane �Same demographic distribution �Same cabin crew © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Human Subjects Designs �Age, sex, experience etc �Bias �Learning �Fatigue �Motivation �Safety – Institutional review board �? ? © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Within and Between Subjects Designs �Within subjects �Each subject participates in all the experimental conditions �Learning effects can be a problem �Between subjects �Separate groups of subjects participate in the different experimental conditions �More subjects are usually needed �Confounding may occur if the groups have different makeup © Brian Peacock Ergonomics (BPE) Pte. Ltd.

Remember – Statistics does not make you wise, it just prevents you from being a fool Don’t jump to conclusions without sufficient evidence Be careful with your experimental designs © Brian Peacock Ergonomics (BPE) Pte. Ltd.