Human Perception 2 Image Formation Studying Reflections from

Human Perception 2: Image Formation

Studying Reflections from the Eye n n Imaging components of the eye Light l l l enters pupil, which is bordered by the iris is brought into focus by the cornea and lens Passes through the transparent vitreous and retinal cell layers 2. 2

Studying Reflections from the Eye n n The beam-splitter Measuring light reflected from the eye 2. 3

Studying Reflections from the Eye n A modified ophthalmoscope 2. 4

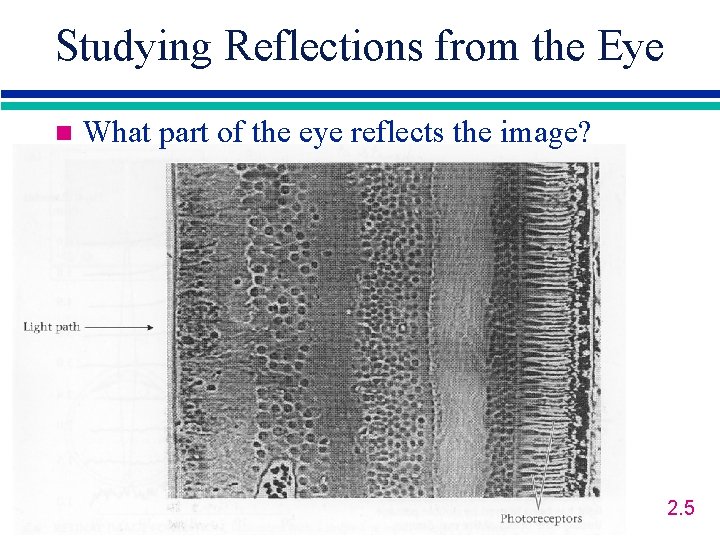
Studying Reflections from the Eye n What part of the eye reflects the image? 2. 5

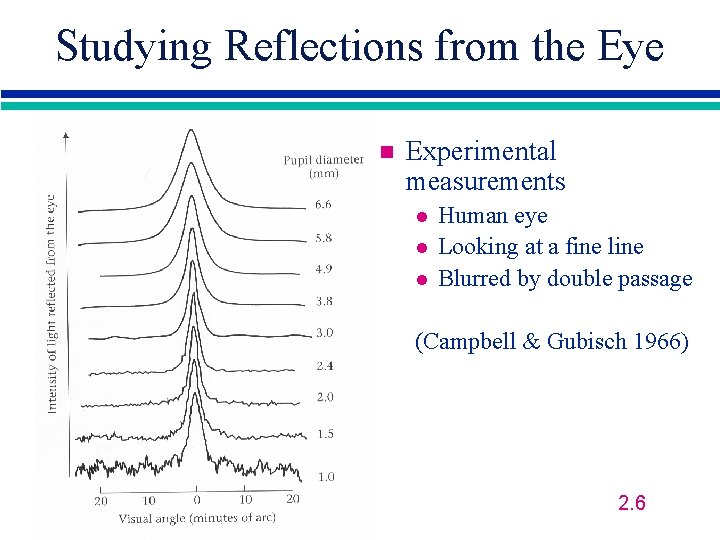
Studying Reflections from the Eye n Experimental measurements l l l Human eye Looking at a fine line Blurred by double passage (Campbell & Gubisch 1966) 2. 6

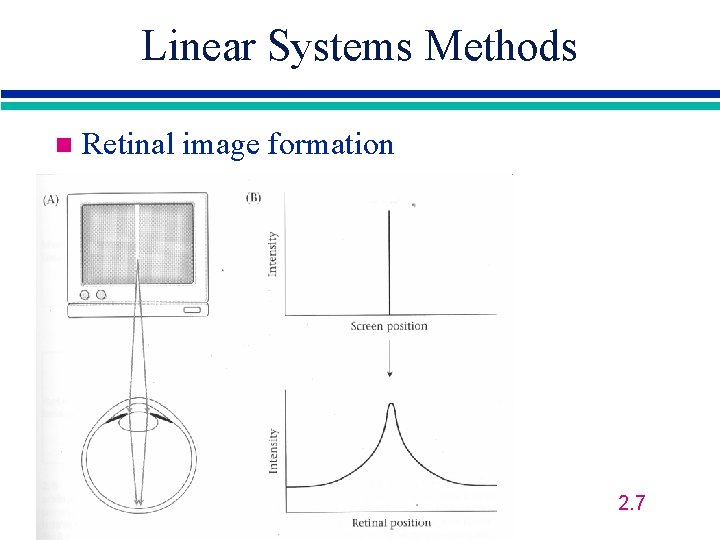
Linear Systems Methods n Retinal image formation 2. 7

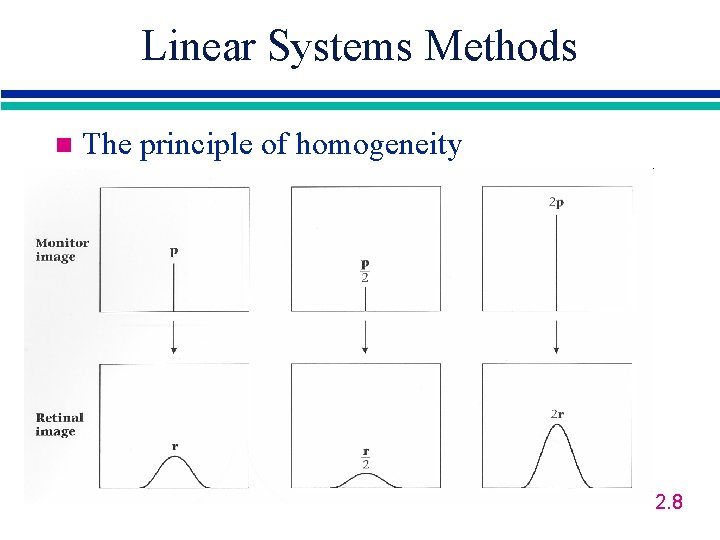
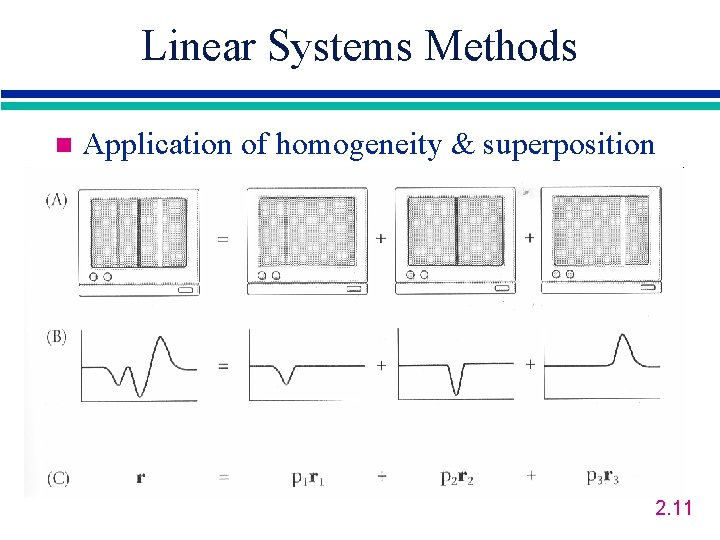
Linear Systems Methods n The principle of homogeneity 2. 8

Linear Systems Methods n The principle of superposition 2. 9

Linear Systems Methods n Linear transform: R=L(P) n Homogeneity: L(a. P)=a. L(P) n Superposition: L(P+P’)=L(P)+L(P’) 2. 10

Linear Systems Methods n Application of homogeneity & superposition 2. 11

Linear Systems Methods n Retinal image formation R=LP vector and matrix representation 2. 12

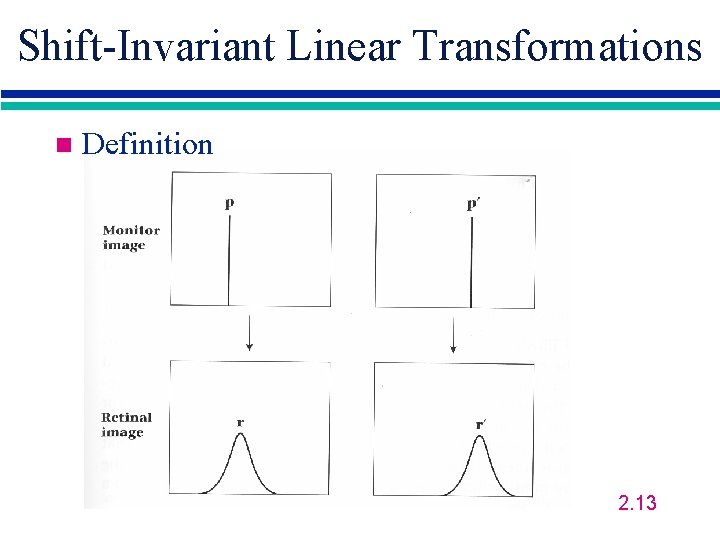
Shift-Invariant Linear Transformations n Definition 2. 13

Shift-Invariant Linear Transformations n Properties The system matrix from the response to a single stimulus l The response to a harmonic function is a harmonic function at the same frequency l cos(2π f i/N) sf cos(2π f i/N + a) 2. 14

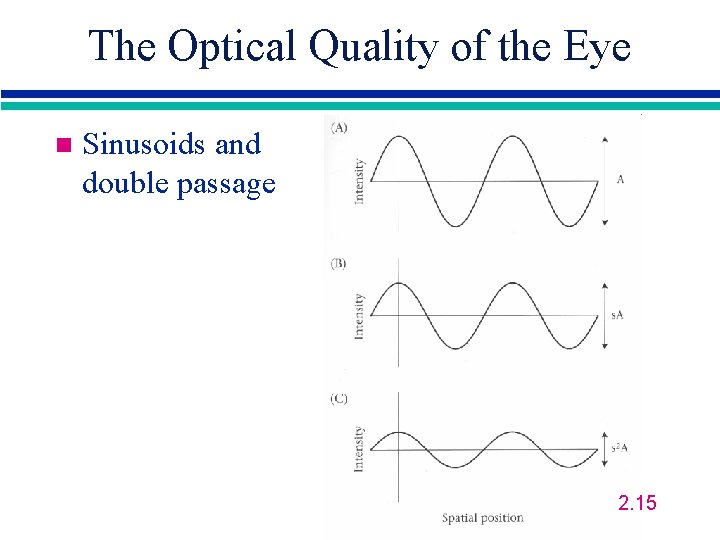
The Optical Quality of the Eye n Sinusoids and double passage 2. 15

The Optical Quality of the Eye Sinusoids and double passage n Image: n P=Σ cos(2π f i/N) n Measurement: R=Σ (sf) 2 cos(2π f i/N) n Single pass at retina: R’=Σ sf cos(2π f i/N) 2. 16

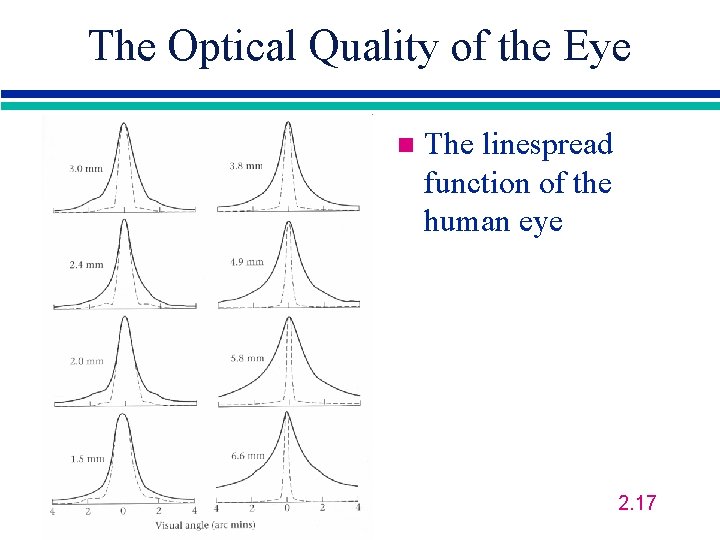
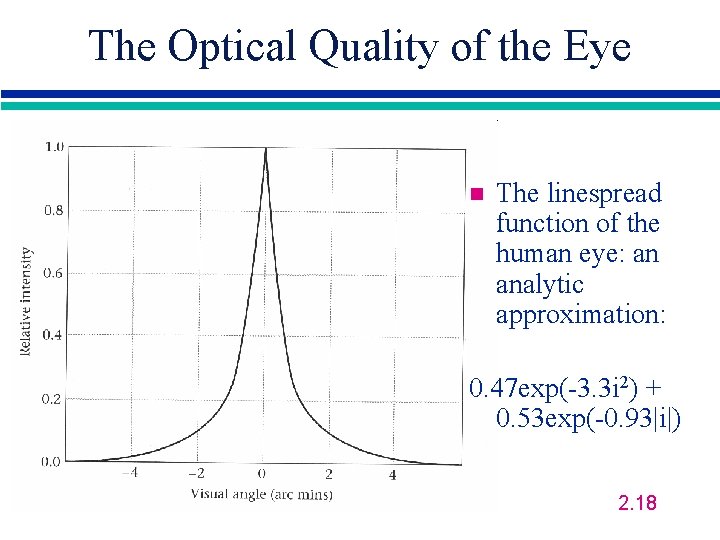
The Optical Quality of the Eye n The linespread function of the human eye 2. 17

The Optical Quality of the Eye n The linespread function of the human eye: an analytic approximation: 0. 47 exp(-3. 3 i 2) + 0. 53 exp(-0. 93|i|) 2. 18

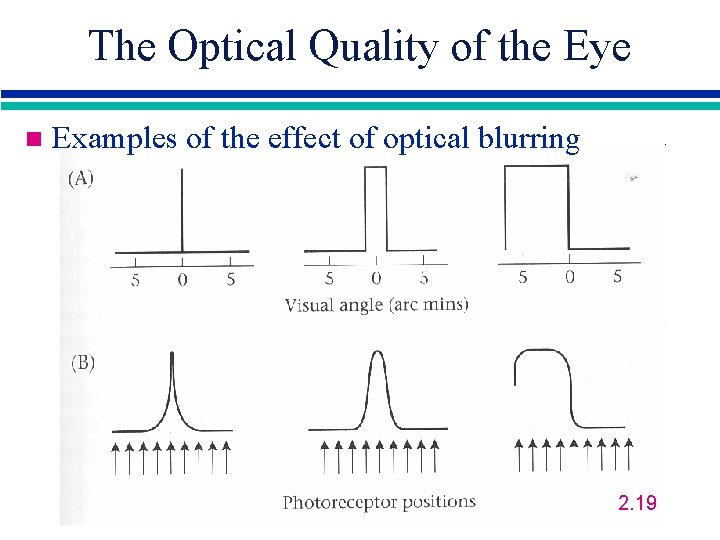
The Optical Quality of the Eye n Examples of the effect of optical blurring 2. 19

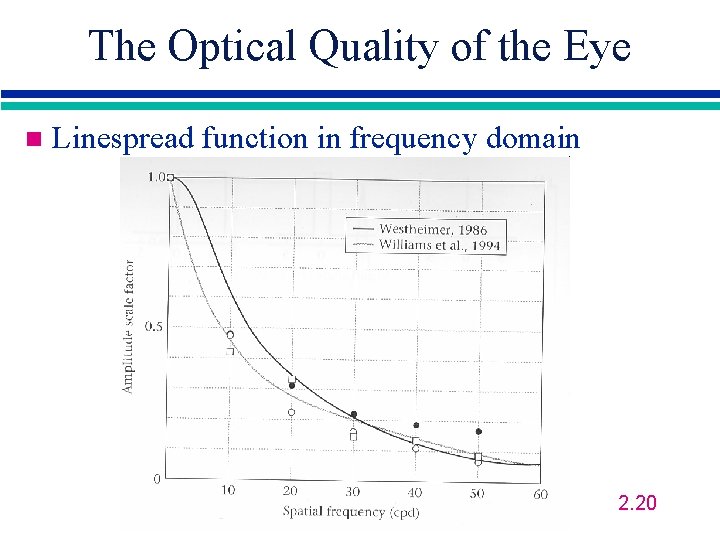
The Optical Quality of the Eye n Linespread function in frequency domain 2. 20

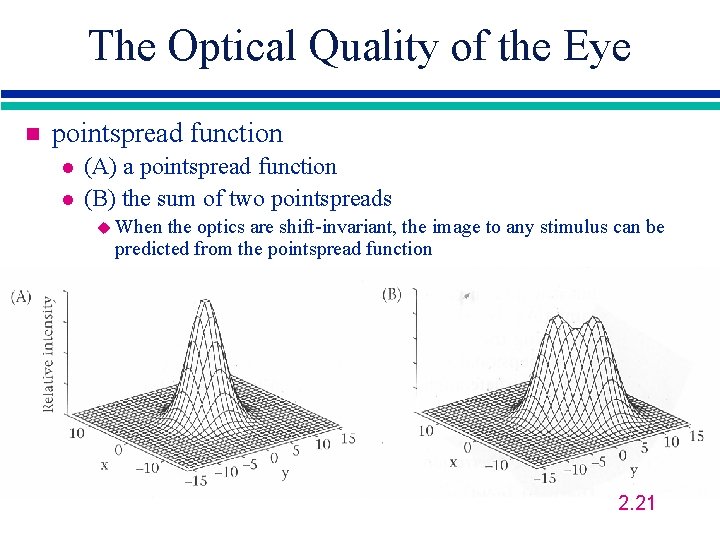
The Optical Quality of the Eye n pointspread function l l (A) a pointspread function (B) the sum of two pointspreads u When the optics are shift-invariant, the image to any stimulus can be predicted from the pointspread function 2. 21