Huffman Coding A simple example Suppose we have

A simple example § Suppose we have a message consisting of 5 symbols, e.

A simple example – cont. § Intuition: Those symbols that are more frequent should

Another Example § A=0 B = 100 C = 1010 D = 1011 R

Huffman codes § Binary character code: each character is represented by a unique binary

Variable-length code § Need some carefulness to read the code. l l 001011101 (codeword:

Using codeword in Table to encode and decode § Encode: abc = 0. 101.

§ Encode: abc = 0. 101. 100 = 0101100 l (just concatenate the codewords.

Binary tree § Every nonleaf node has two children. l Why? § The fixed-length

Constructing an optimal coding scheme § Formal definition of the problem: § Input: a

(a) (b) f: 5 c: 12 e: 9 c: 12 b: 13 14 0

HUFFMAN(C) 1 n: =|C| 2 Q: =C 3 for i: =1 to n-1 do

The Huffman Algorithm § This algorithm builds the tree T corresponding to the optimal

Time complexity § Lines 4 -8 are executed n-1 times. § Each heap operation

An Complete Example Scan the original text Eerie eyes seen near lake. § What

Building a Tree Scan the original text Eerie eyes seen near lake. § What

Building a Tree § The array after inserting all nodes E i y l

Building a Tree 26 16 10 4 2 E 1 i 1 e 8

Building a Tree After enqueueing this node there is only one node left in

Exercise Modify My. Heap. java in Tutorial 6’s folder so that the class Array.

Slides: 77

Download presentation

Huffman Coding

A simple example § Suppose we have a message consisting of 5 symbols, e. g. [►♣♣♠☻►♣☼►☻] § How can we code this message using 0/1 so the coded message will have minimum length (for transmission or saving!) § 5 symbols at least 3 bits § For a simple encoding, length of code is 10*3=30 bits

A simple example – cont. § Intuition: Those symbols that are more frequent should have smaller codes, yet since their length is not the same, there must be a way of distinguishing each code § For Huffman code, length of encoded message will be ►♣♣♠☻►♣☼►☻ =3*2 +3*2+2*2+3+3=24 bits

Another Example § A=0 B = 100 C = 1010 D = 1011 R = 11 § ABRACADABRA = 01001101010010110100110 § This is eleven letters in 23 bits § A fixed-width encoding would require 3 bits for five different letters, or 33 bits for 11 letters § Notice that the encoded bit string can be decoded!

Huffman codes § Binary character code: each character is represented by a unique binary string. § A data file can be coded in two ways: a b c d e f frequency(%) 45 13 12 16 9 5 fixed-length code 000 001 010 011 100 101 variable-length code 0 101 100 111 1100 The first way needs 100 3=300 bits. The second way needs 45 1+13 3+12 3+16 3+9 4+5 4=232 bits. 2021/2/26 Page 5

Variable-length code § Need some carefulness to read the code. l l 001011101 (codeword: a=0, b=00, c=01, d=11. ) Where to cut? 00 can be explained as either aa or b. § Prefix of 0011: 0, 001, and 0011. § Prefix codes: no codeword is a prefix of some other codeword. (prefix free) § Prefix codes are simple to encode and decode. Page 6 2021/2/26

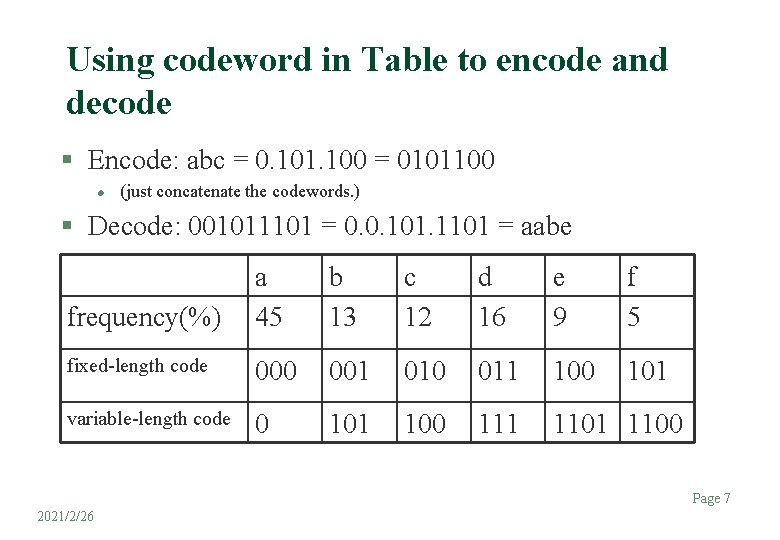
Using codeword in Table to encode and decode § Encode: abc = 0. 101. 100 = 0101100 l (just concatenate the codewords. ) § Decode: 001011101 = 0. 0. 101. 1101 = aabe frequency(%) a 45 b 13 c 12 d 16 e 9 f 5 fixed-length code 000 001 010 011 100 101 variable-length code 0 101 100 111 1100 Page 7 2021/2/26

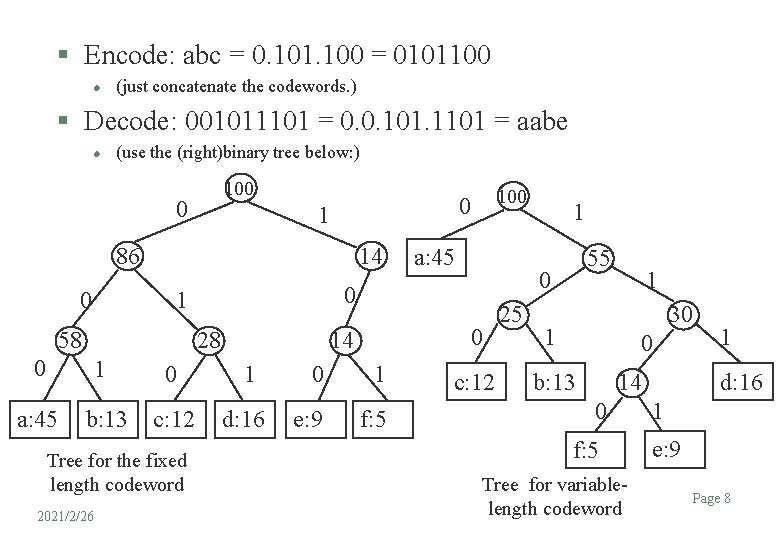
§ Encode: abc = 0. 101. 100 = 0101100 l (just concatenate the codewords. ) § Decode: 001011101 = 0. 0. 101. 1101 = aabe l (use the (right)binary tree below: ) 100 0 1 14 86 0 0 1 a: 45 b: 13 c: 12 d: 16 2021/2/26 0 1 e: 9 f: 5 1 55 0 0 14 28 Tree for the fixed length codeword a: 45 0 1 58 100 0 c: 12 25 1 30 1 0 b: 13 14 0 f: 5 Tree for variablelength codeword 1 d: 16 1 e: 9 Page 8

Binary tree § Every nonleaf node has two children. l Why? § The fixed-length code in our example is not optimal. § The total number of bits required to encode a file is l l f ( c ) : the frequency (number of occurrences) of c in the file d. T(c): denote the depth of c’s leaf in the tree Page 9 2021/2/26

Constructing an optimal coding scheme § Formal definition of the problem: § Input: a set of characters C={c 1, c 2, …, cn}, each c C has frequency f[c]. § Output: a binary tree representing codewords so that the total number of bits required for the file is minimized. § Huffman proposed a greedy algorithm to solve the problem. Page 10 2021/2/26

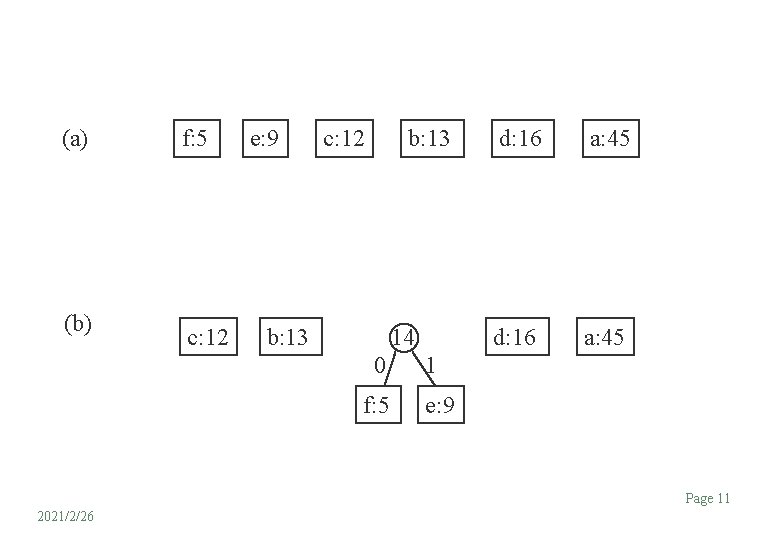
(a) (b) f: 5 c: 12 e: 9 c: 12 b: 13 14 0 f: 5 d: 16 a: 45 1 e: 9 Page 11 2021/2/26

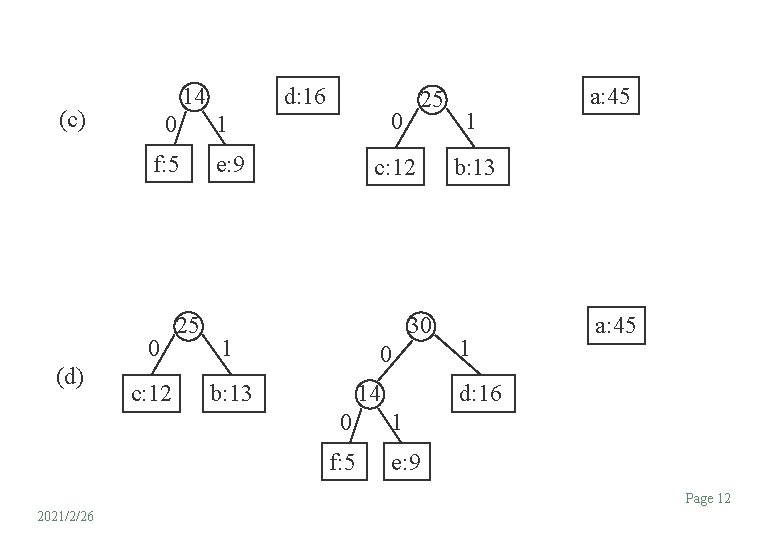
14 (c) 0 f: 5 0 (d) c: 12 25 d: 16 25 0 1 e: 9 c: 12 30 1 0 b: 13 14 0 f: 5 1 a: 45 b: 13 1 a: 45 d: 16 1 e: 9 Page 12 2021/2/26

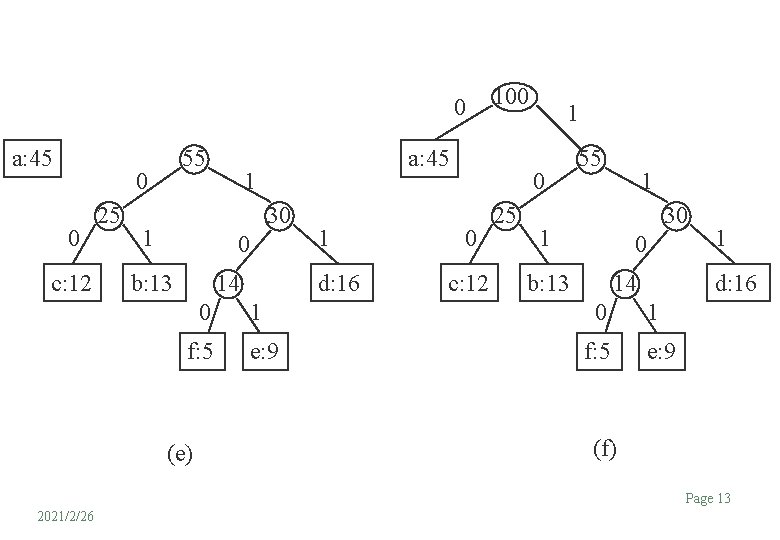
0 a: 45 55 0 0 c: 12 25 a: 45 1 30 1 0 14 b: 13 0 f: 5 (e) 100 1 d: 16 1 e: 9 1 0 0 c: 12 25 55 1 30 1 0 b: 13 14 0 f: 5 1 d: 16 1 e: 9 (f) Page 13 2021/2/26

HUFFMAN(C) 1 n: =|C| 2 Q: =C 3 for i: =1 to n-1 do 4 z: =ALLOCATE_NODE() 5 x: =left[z]: =EXTRACT_MIN(Q) 6 y: =right[z]: =EXTRACT_MIN(Q) 7 f[z]: =f[x]+f[y] 8 INSERT(Q, z) 9 return EXTRACT_MIN(Q) Page 14 2021/2/26

The Huffman Algorithm § This algorithm builds the tree T corresponding to the optimal code in a bottom-up manner. § C is a set of n characters, and each character c in C is a character with a defined frequency f[c]. § Q is a priority queue, keyed on f, used to identify the two least-frequent characters to merge together. § The result of the merger is a new object (internal node) whose frequency is the sum of the two objects. Page 15 2021/2/26

Time complexity § Lines 4 -8 are executed n-1 times. § Each heap operation in Lines 4 -8 takes O(lg n) time. § Total time required is O(n lg n). Note: The details of heap operation will not be tested. Time complexity O(n lg n) should be remembered. Page 16 2021/2/26

An Complete Example Scan the original text Eerie eyes seen near lake. § What characters are present? E e r i space ysnalk.

Building a Tree Scan the original text Eerie eyes seen near lake. § What is the frequency of each character in the text? Char Freq. E 1 e 8 r 2 i 1 space 4 Char Freq. y 1 s 2 n 2 a 2 l 1 Char Freq. k 1. 1

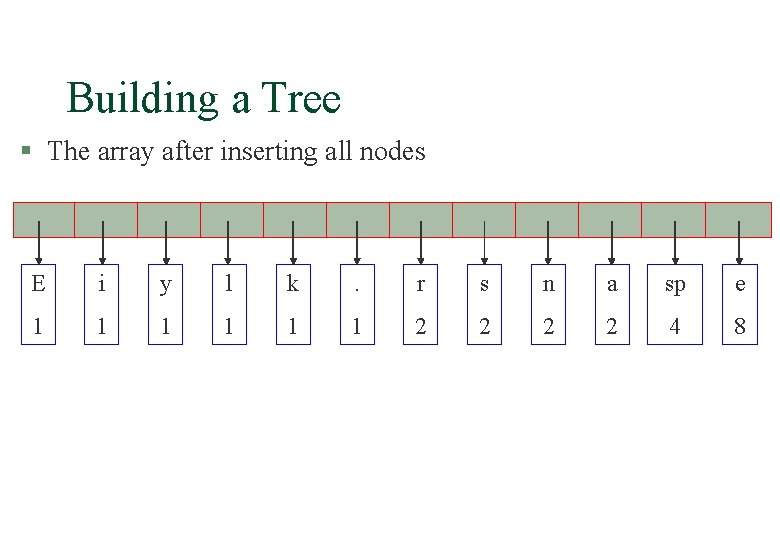
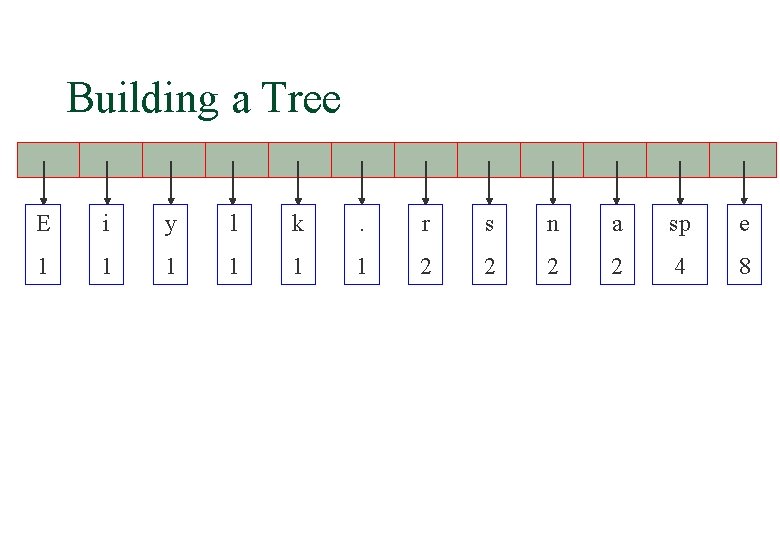
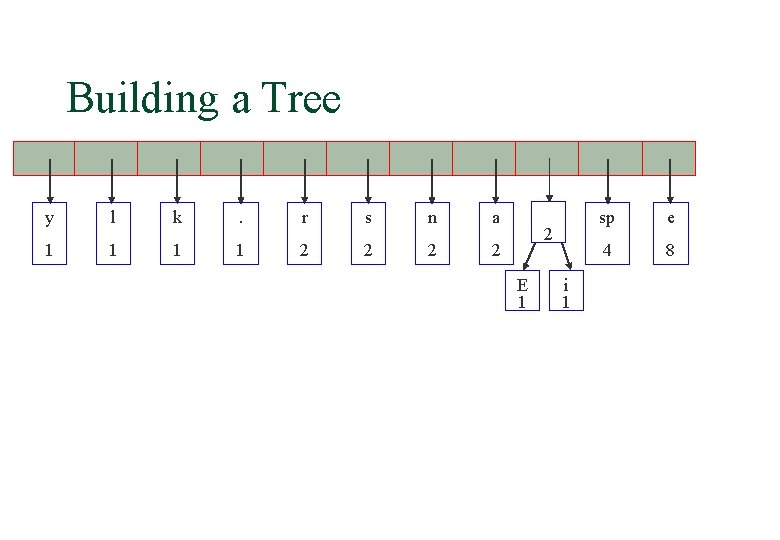
Building a Tree § The array after inserting all nodes E i y l k . r s n a sp e 1 1 1 2 2 4 8

Building a Tree E i y l k . r s n a sp e 1 1 1 2 2 4 8

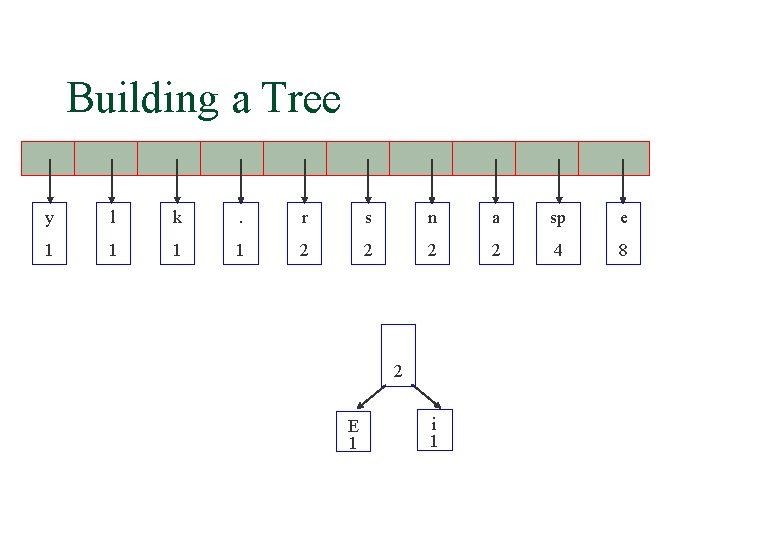
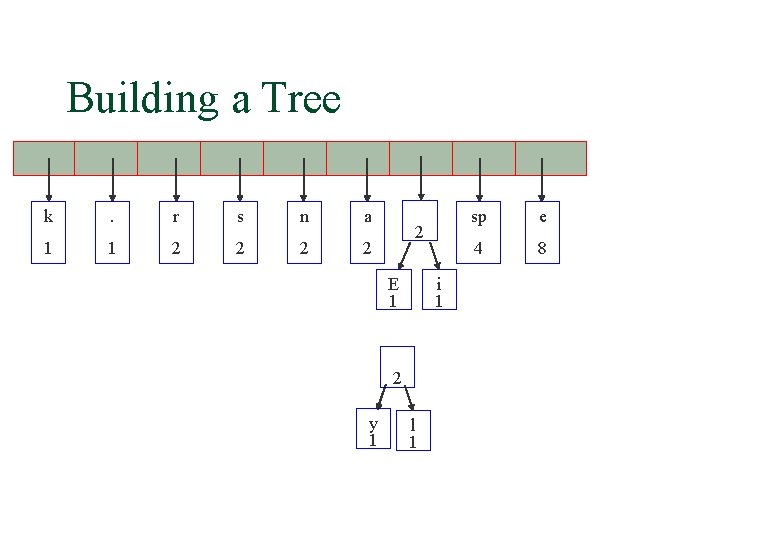
Building a Tree y l k . r s n a sp e 1 1 2 2 4 8 2 E 1 i 1

Building a Tree y l k . r s n a 1 1 2 2 2 E 1 i 1 sp e 4 8

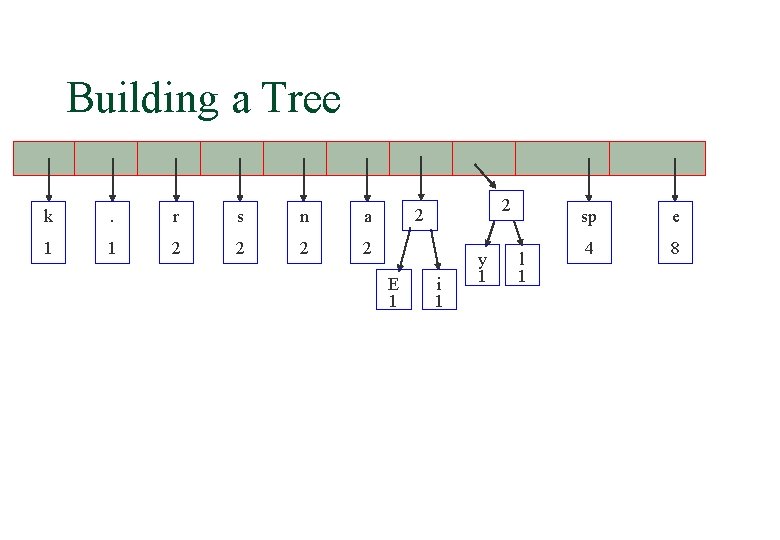
Building a Tree k . r s n a 1 1 2 2 2 E 1 i 1 2 y 1 l 1 sp e 4 8

Building a Tree k . r s n a 1 1 2 2 2 E 1 i 1 y 1 l 1 sp e 4 8

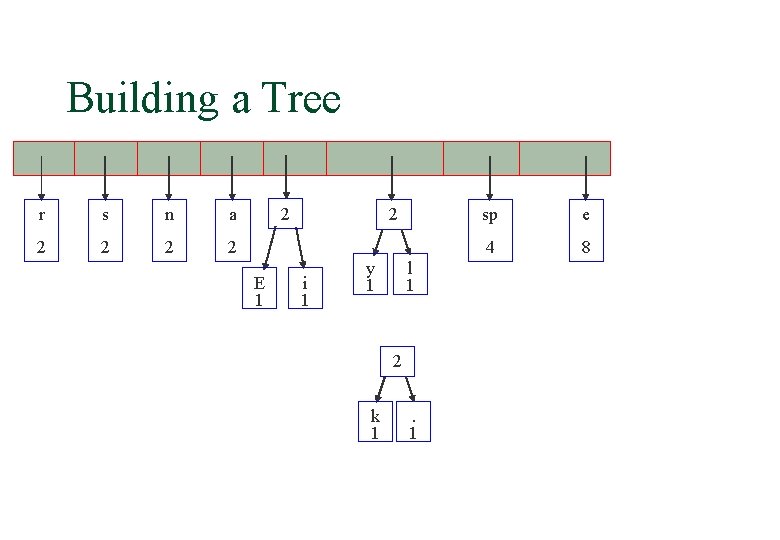
Building a Tree r s n a 2 2 2 E 1 2 i 1 y 1 l 1 2 k 1 . 1 sp e 4 8

Building a Tree r s n a 2 2 2 E 1 2 2 i 1 y 1 l 1 k 1 . 1 sp e 4 8

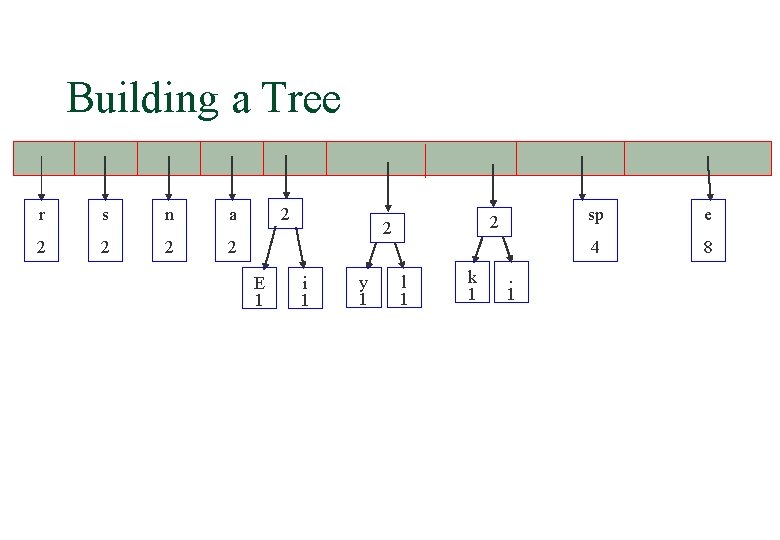
Building a Tree n 2 a 2 2 2 E 1 i 1 y 1 2 l 1 k 1 4 r 2 s 2 . 1 sp e 4 8

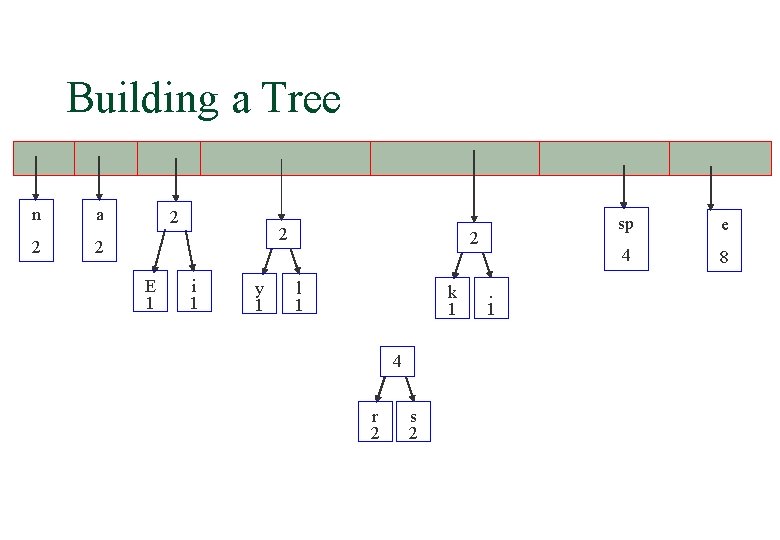
Building a Tree n a 2 2 2 E 1 2 i 1 y 1 sp 2 e 4 8 4 l 1 k 1 . 1 r 2 s 2

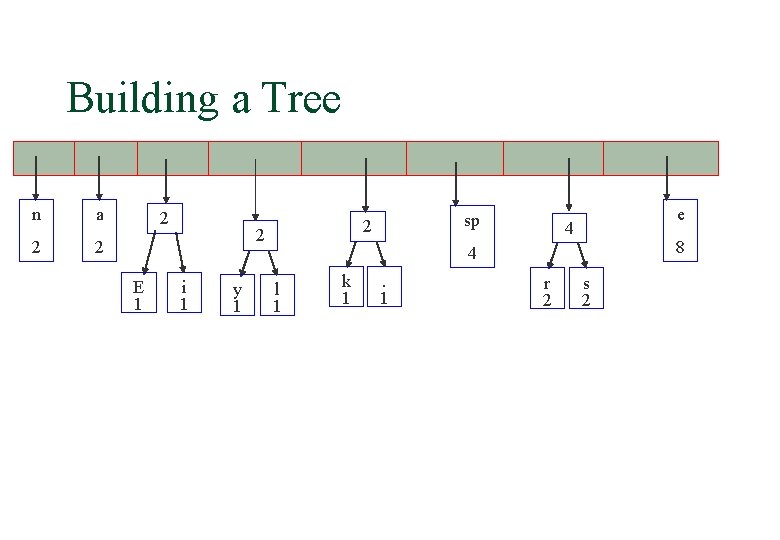
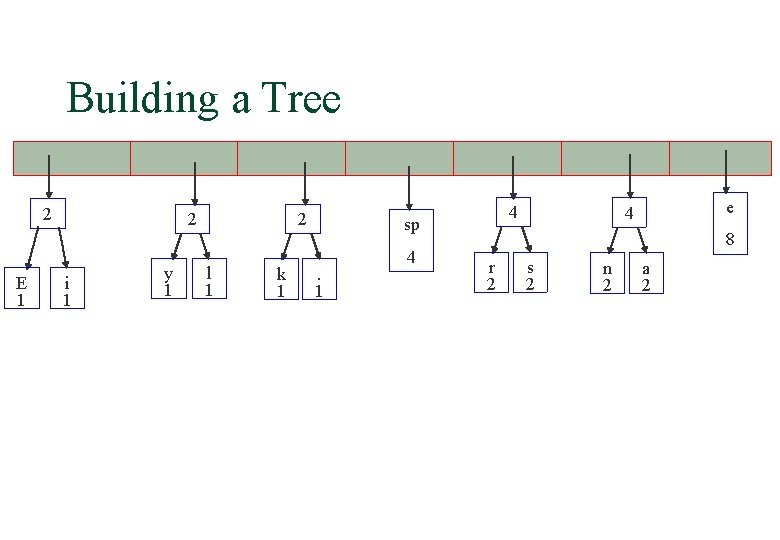
Building a Tree 2 E 1 2 i 1 y 1 2 l 1 k 1 sp 4 . 1 4 n 2 a 2 e 4 8 r 2 s 2

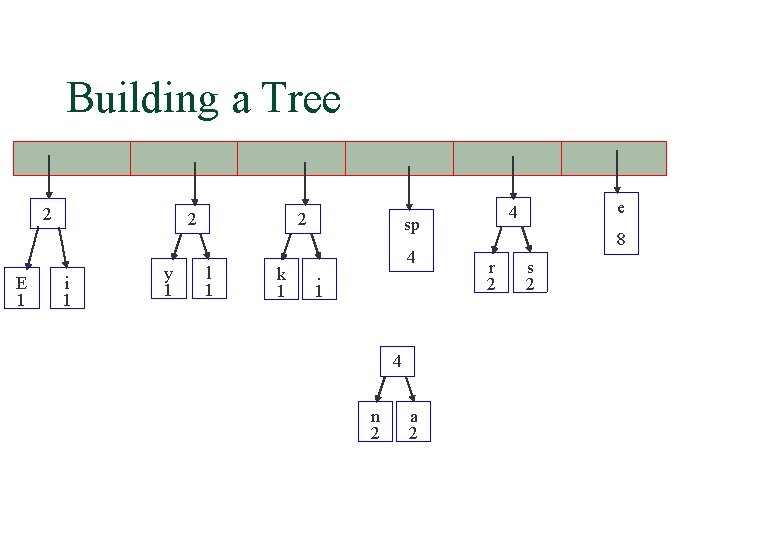
Building a Tree 2 E 1 2 i 1 y 1 2 l 1 k 1 4 sp. 1 4 e 4 8 r 2 s 2 n 2 a 2

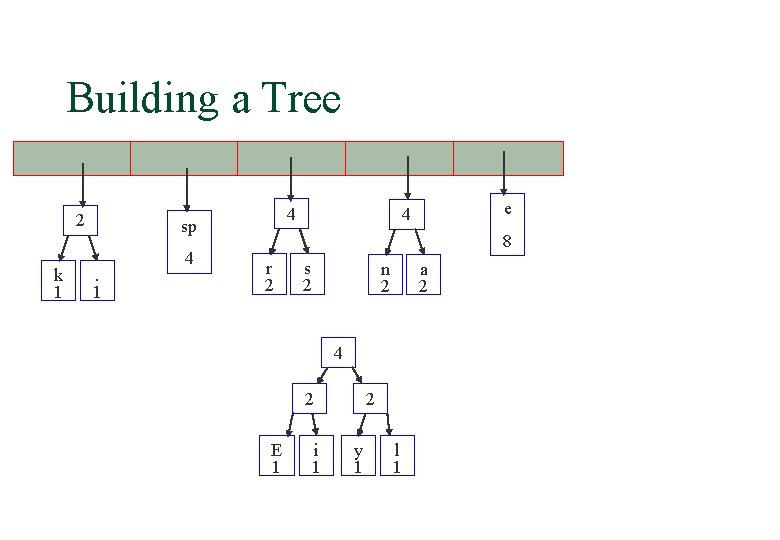
Building a Tree 2 k 1 4 sp. 1 4 e 4 8 r 2 s 2 n 2 a 2 4 2 E 1 i 1 2 y 1 l 1

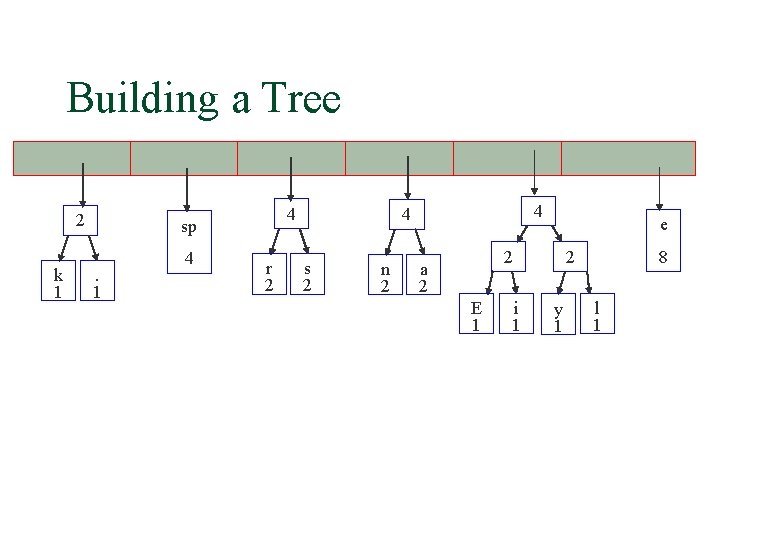
Building a Tree 2 k 1 4 sp. 1 4 r 2 4 4 s 2 n 2 e 2 a 2 E 1 i 1 8 2 y 1 l 1

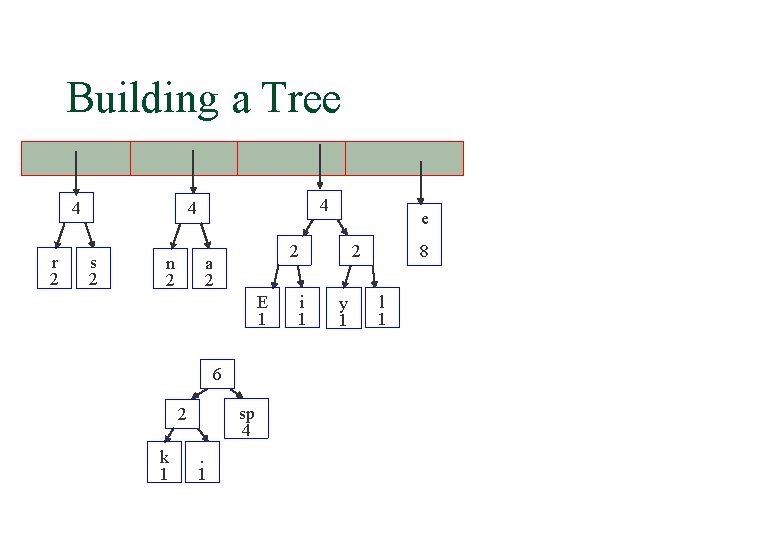
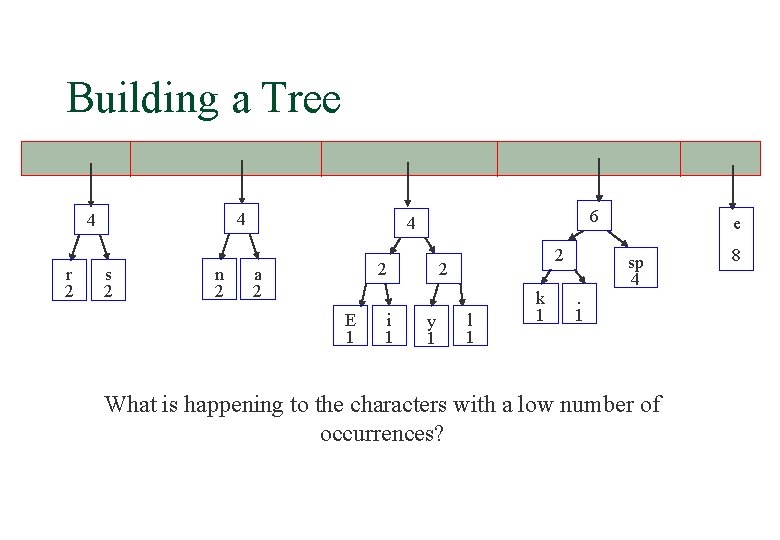
Building a Tree 4 r 2 4 4 s 2 n 2 2 a 2 E 1 6 sp 4 2 k 1 . 1 e i 1 8 2 y 1 l 1

Building a Tree 4 4 r 2 s 2 n 2 6 4 2 a 2 E 1 i 1 2 2 y 1 l 1 k 1 . 1 e sp 4 What is happening to the characters with a low number of occurrences? 8

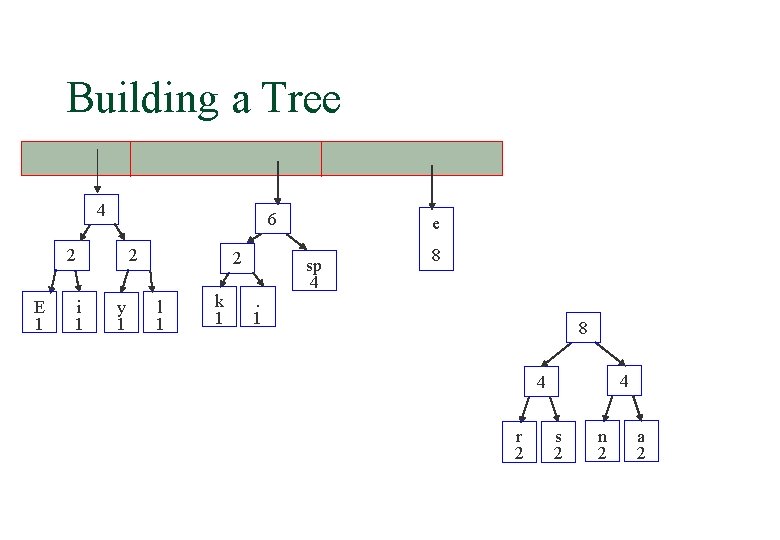
Building a Tree 4 6 2 E 1 i 1 2 y 1 2 l 1 k 1 . 1 e sp 4 8 8 4 4 r 2 s 2 n 2 a 2

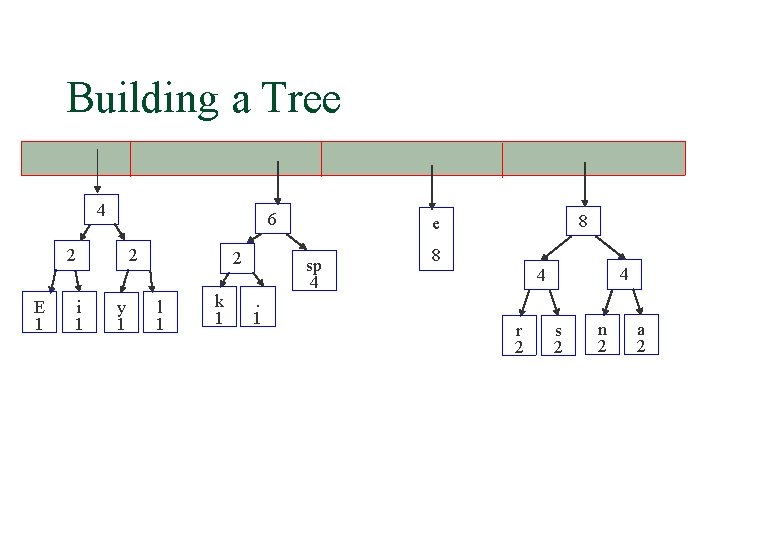
Building a Tree 4 6 2 E 1 i 1 2 y 1 2 l 1 k 1 . 1 8 e sp 4 8 4 4 r 2 s 2 n 2 a 2

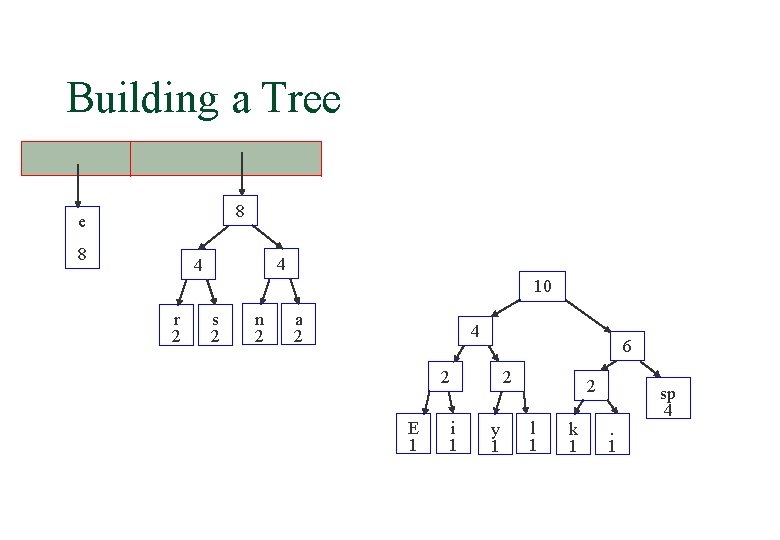
Building a Tree 8 4 4 10 r 2 s 2 n 2 a 2 4 6 2 E 1 i 1 2 y 1 2 l 1 k 1 . 1 sp 4

Building a Tree 8 10 r 2 4 4 4 s 2 n 2 6 2 a 2 E 1 i 1 2 y 1 2 l 1 k 1 . 1 sp 4

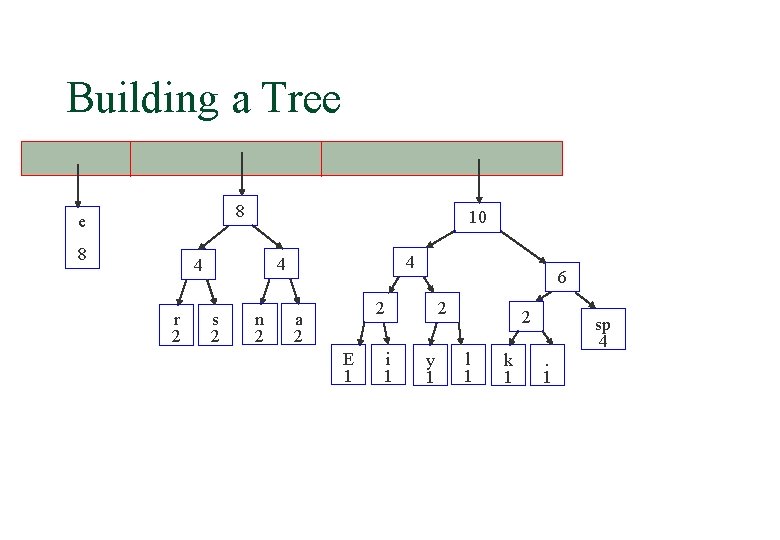
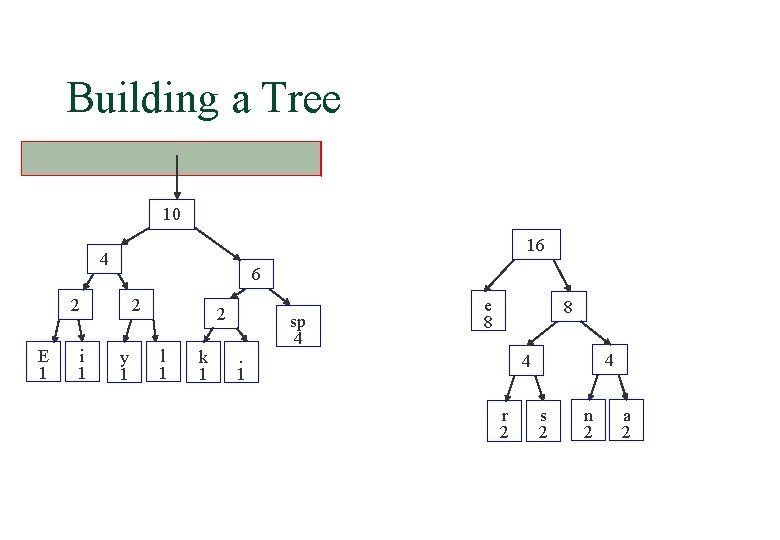
Building a Tree 10 16 4 6 2 E 1 i 1 2 y 1 2 l 1 k 1 . 1 sp 4 e 8 8 4 4 r 2 s 2 n 2 a 2

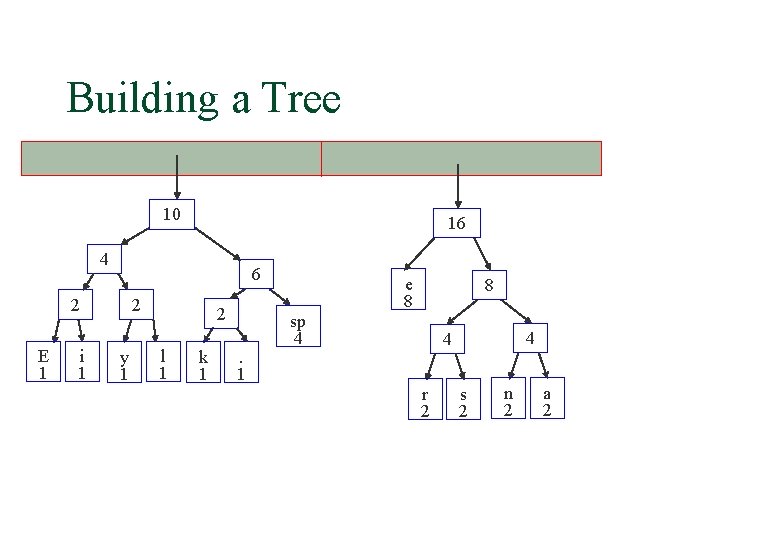
Building a Tree 10 16 4 6 2 E 1 i 1 2 y 1 2 l 1 k 1 . 1 e 8 8 sp 4 4 4 r 2 s 2 n 2 a 2

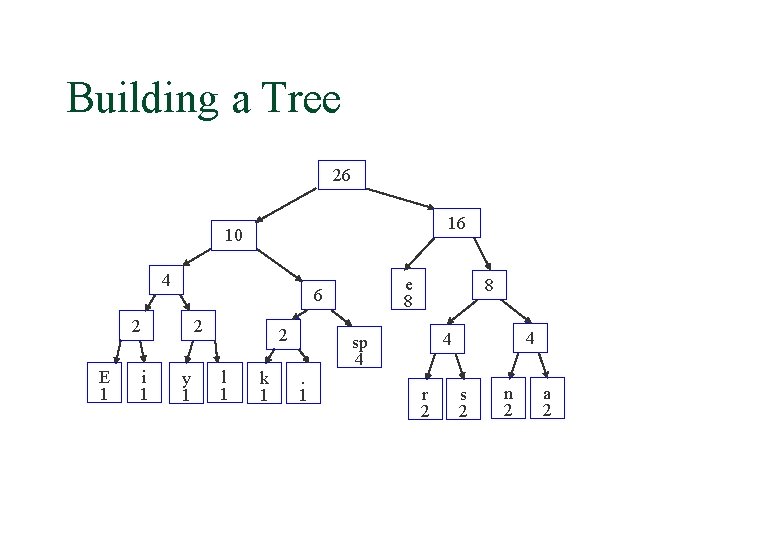
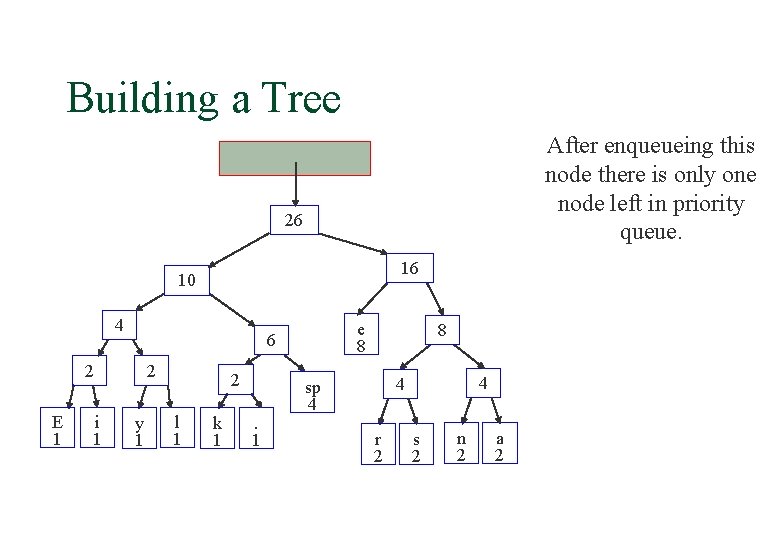
Building a Tree 26 16 10 4 2 E 1 i 1 e 8 6 2 y 1 2 l 1 k 1 . 1 8 4 4 sp 4 r 2 s 2 n 2 a 2

Building a Tree After enqueueing this node there is only one node left in priority queue. 26 16 10 4 2 E 1 i 1 e 8 6 2 y 1 2 l 1 k 1 . 1 8 4 4 sp 4 r 2 s 2 n 2 a 2

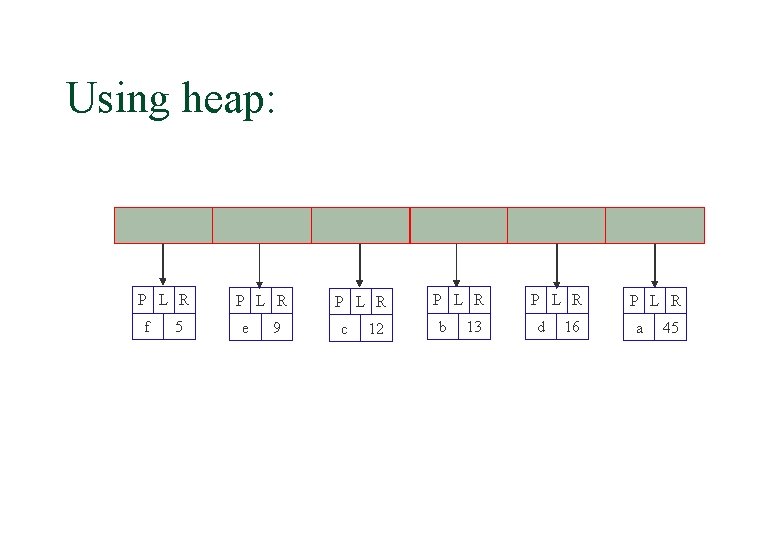
Using heap: P L R f 5 P L R e 9 P L R c 12 P L R b 13 P L R d 16 P L R a 45

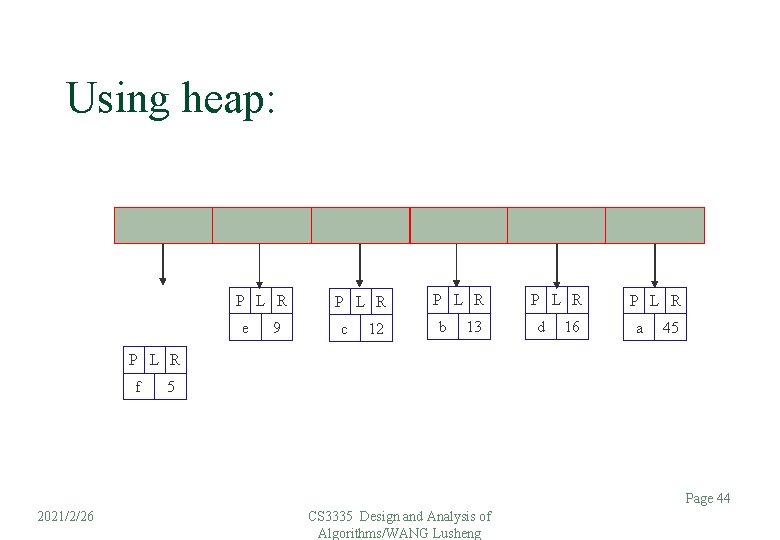
Using heap: P L R e 9 P L R c 12 P L R b 13 P L R d 16 P L R a 45 P L R f 5 Page 44 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

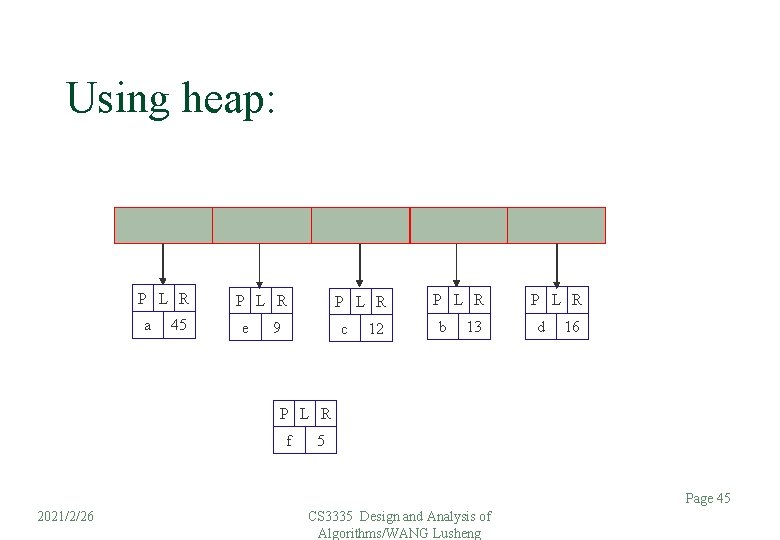
Using heap: P L R a 45 P L R e P L R 9 c 12 P L R b 13 P L R d 16 P L R f 5 Page 45 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

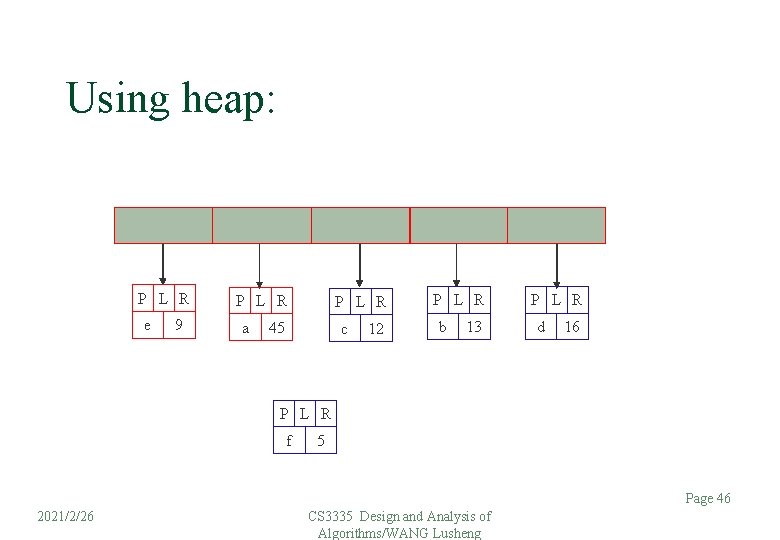
Using heap: P L R e 9 P L R a P L R 45 c 12 P L R b 13 P L R d 16 P L R f 5 Page 46 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

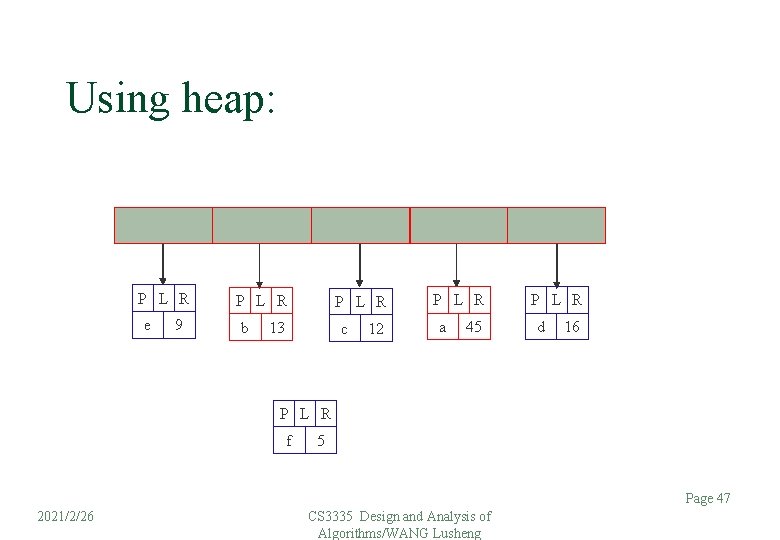
Using heap: P L R e 9 P L R b P L R 13 c 12 P L R a 45 P L R d 16 P L R f 5 Page 47 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

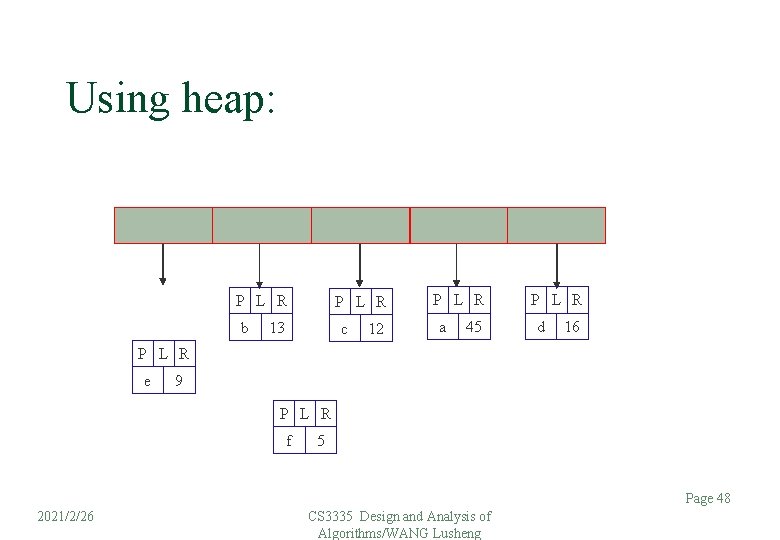
Using heap: P L R b P L R 13 c 12 P L R a 45 P L R d 16 P L R e 9 P L R f 5 Page 48 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

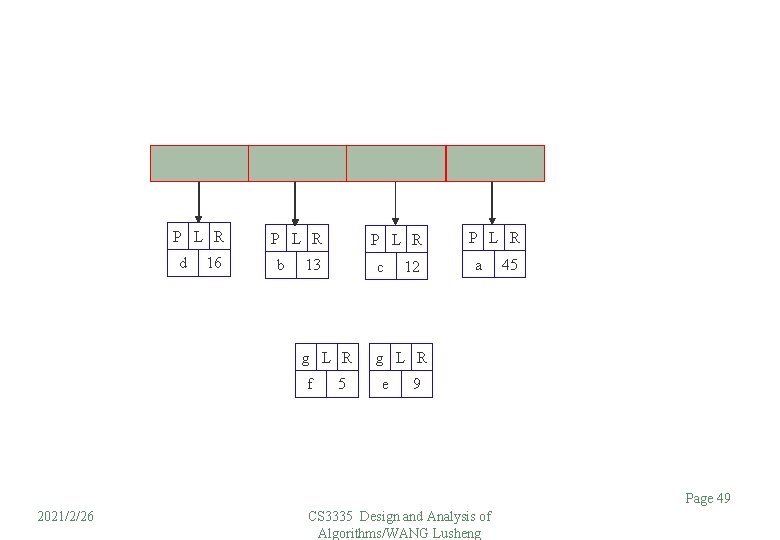
P L R d 16 P L R b P L R 13 c g L R f 5 e 12 P L R a 45 9 Page 49 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

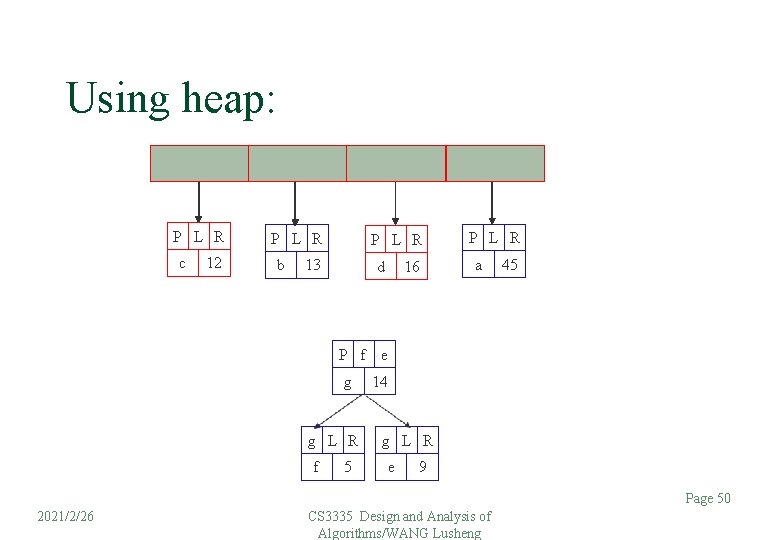
Using heap: P L R c 12 P L R b P L R 13 d 16 P L R a 45 P f e g g L R f 5 14 g L R e 9 Page 50 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

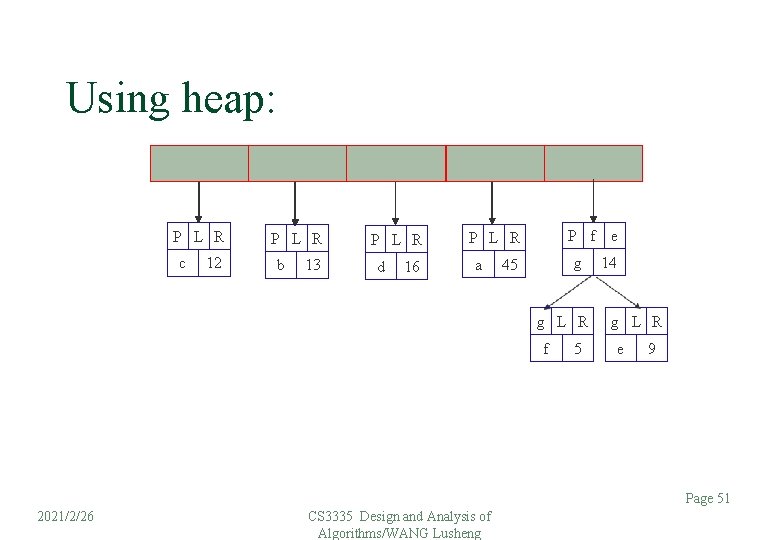
Using heap: P L R c 12 P L R b 13 P L R d 16 P f e P L R a g 45 g L R f 5 14 g L R e 9 Page 51 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

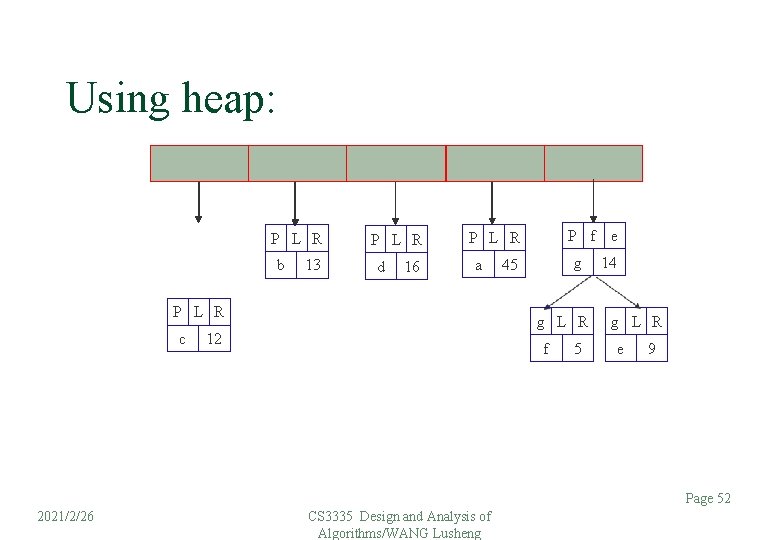
Using heap: P L R b 13 P L R d 16 a P L R c P f e P L R g 45 g L R 12 f 5 14 g L R e 9 Page 52 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

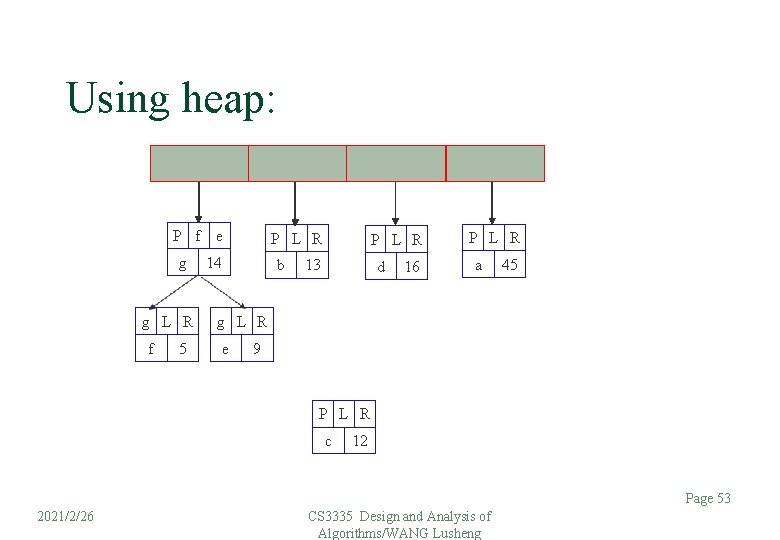
Using heap: P f e g g L R f 5 P L R 14 b P L R 13 d 16 P L R a 45 g L R e 9 P L R c 12 Page 53 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

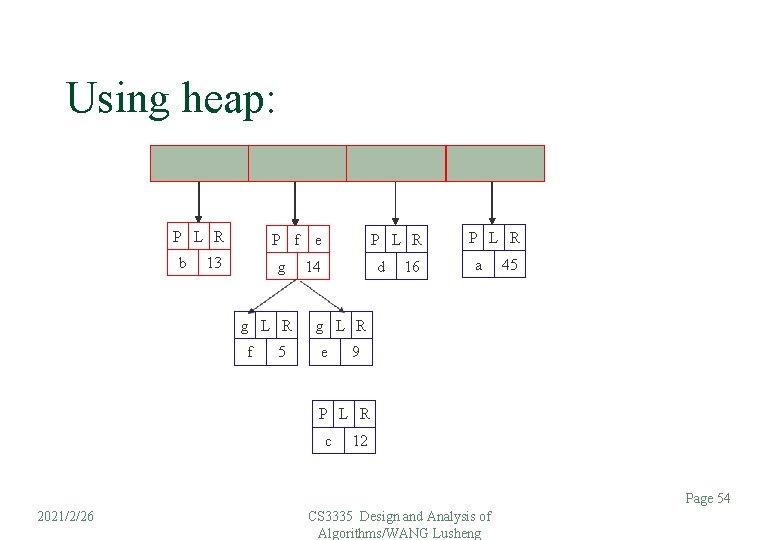
Using heap: P L R b P f e 13 g g L R f 5 P L R 14 d 16 P L R a 45 g L R e 9 P L R c 12 Page 54 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

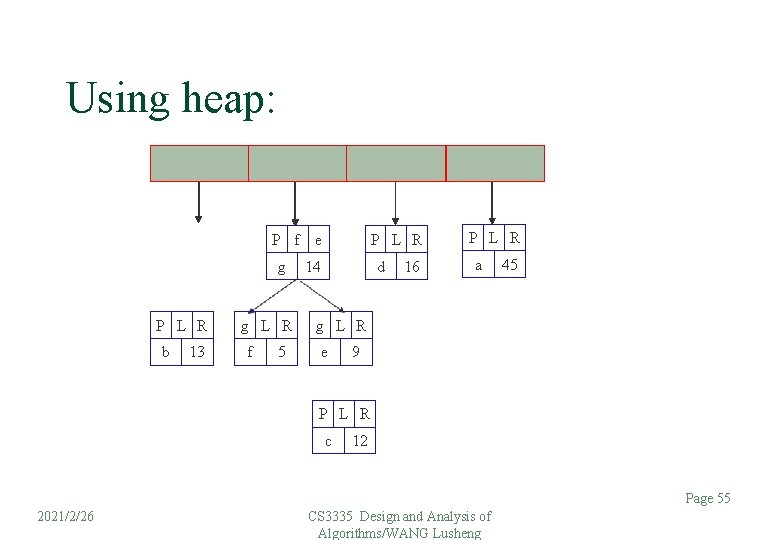
Using heap: P f e g P L R b 13 g L R f 5 P L R 14 d 16 P L R a 45 g L R e 9 P L R c 12 Page 55 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

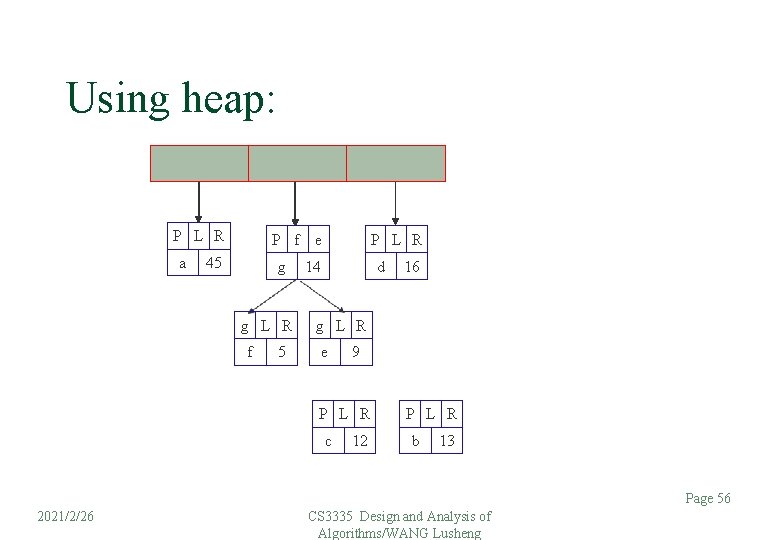
Using heap: P L R a P f e 45 g g L R f 5 P L R 14 d 16 g L R e 9 P L R c 12 P L R b 13 Page 56 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

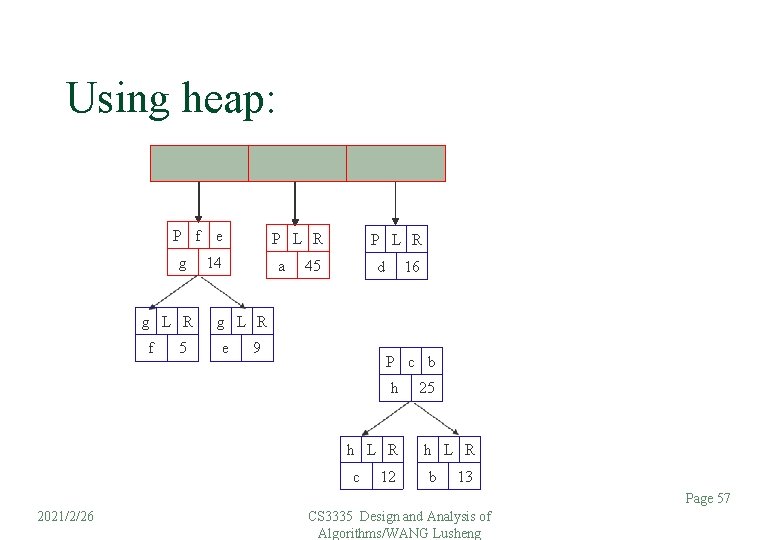
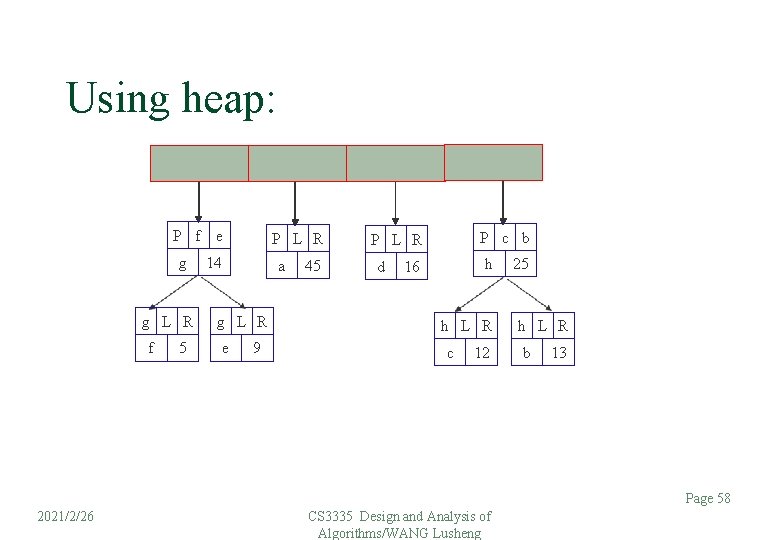
Using heap: P f e g g L R f 5 P L R 14 a P L R 45 d 16 g L R e 9 P c b h h L R c 12 25 h L R b 13 Page 57 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

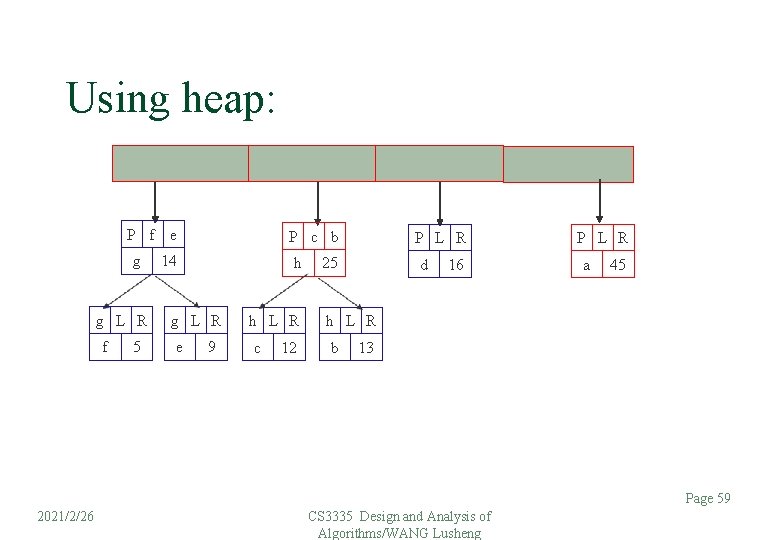
Using heap: P f e g g L R f 5 P L R 14 a g L R e 9 45 P c b P L R d h 16 h L R c 12 25 h L R b 13 Page 58 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

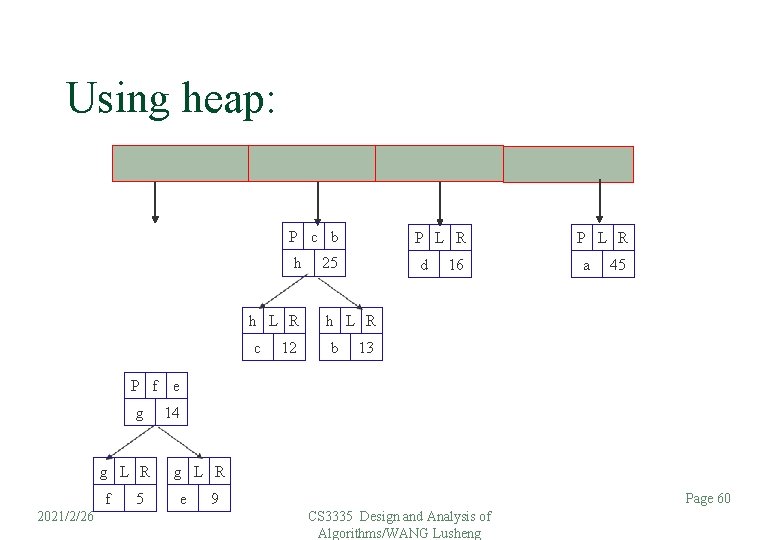
Using heap: P f e g g L R f 5 P c b 14 h g L R e 9 h L R c 12 P L R 25 d 16 P L R a 45 h L R b 13 Page 59 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

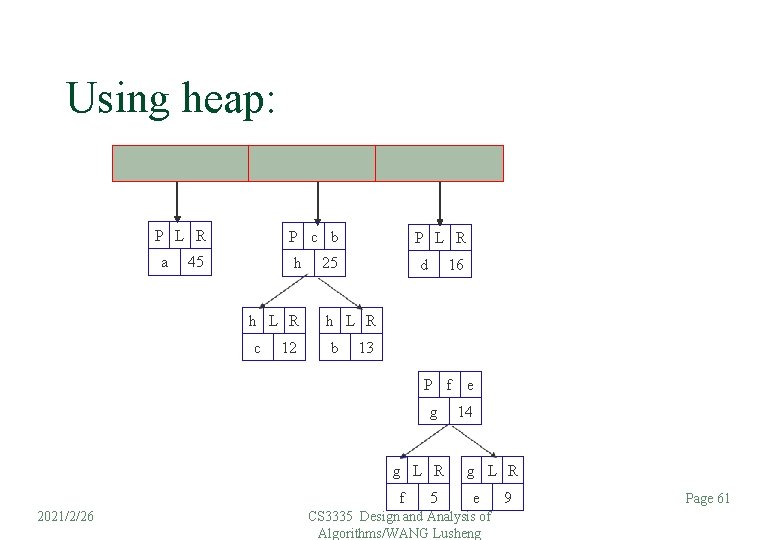
Using heap: P c b h h L R c 12 P L R 25 d 16 P L R a 45 h L R b 13 P f e g g L R f 2021/2/26 5 14 g L R e 9 Page 60 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

Using heap: P L R a P c b 45 h h L R c 12 P L R 25 d 16 h L R b 13 P f e g g L R f 2021/2/26 5 14 g L R e CS 3335 Design and Analysis of Algorithms/WANG Lusheng 9 Page 61

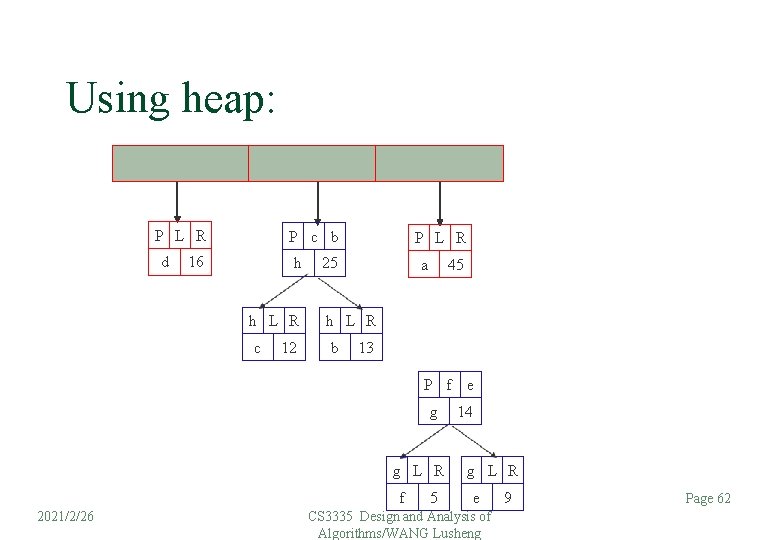
Using heap: P L R d P c b 16 h h L R c 12 P L R 25 a 45 h L R b 13 P f e g g L R f 2021/2/26 5 14 g L R e CS 3335 Design and Analysis of Algorithms/WANG Lusheng 9 Page 62

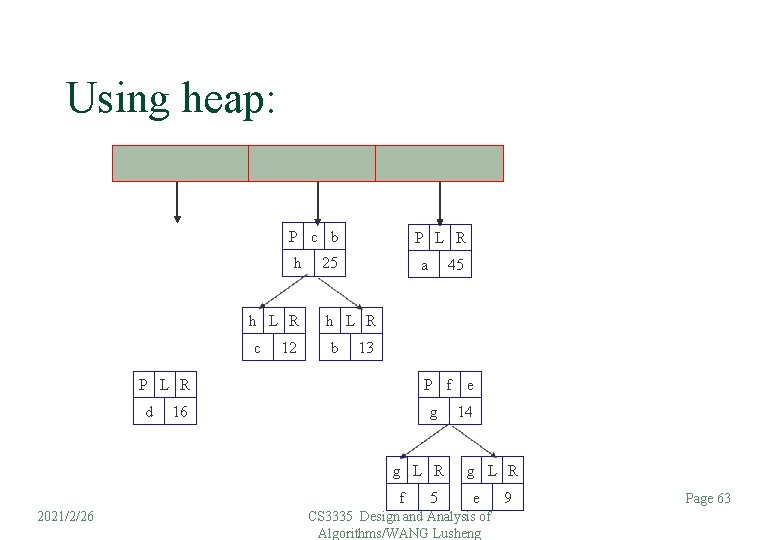
Using heap: P c b h h L R c 12 P L R 25 a h L R b 13 P L R d 45 P f e 16 g g L R f 2021/2/26 5 14 g L R e CS 3335 Design and Analysis of Algorithms/WANG Lusheng 9 Page 63

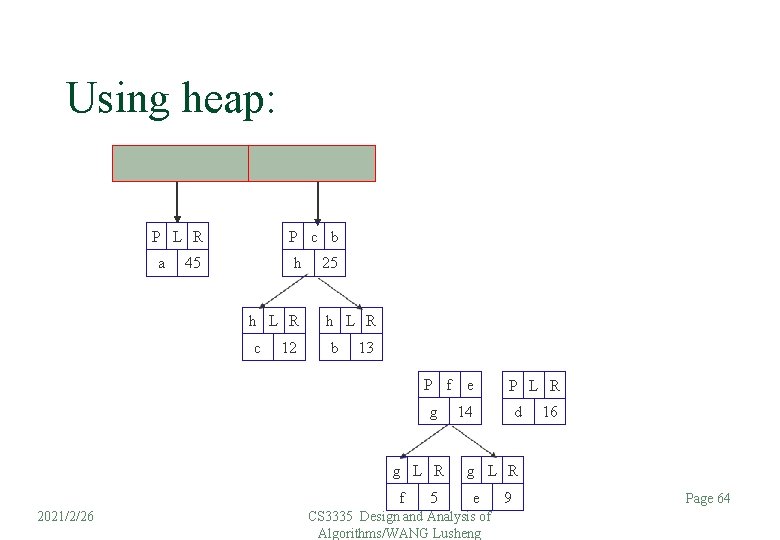
Using heap: P L R a P c b 45 h h L R c 12 25 h L R b 13 P f e g g L R f 2021/2/26 5 P L R 14 d 16 g L R e CS 3335 Design and Analysis of Algorithms/WANG Lusheng 9 Page 64

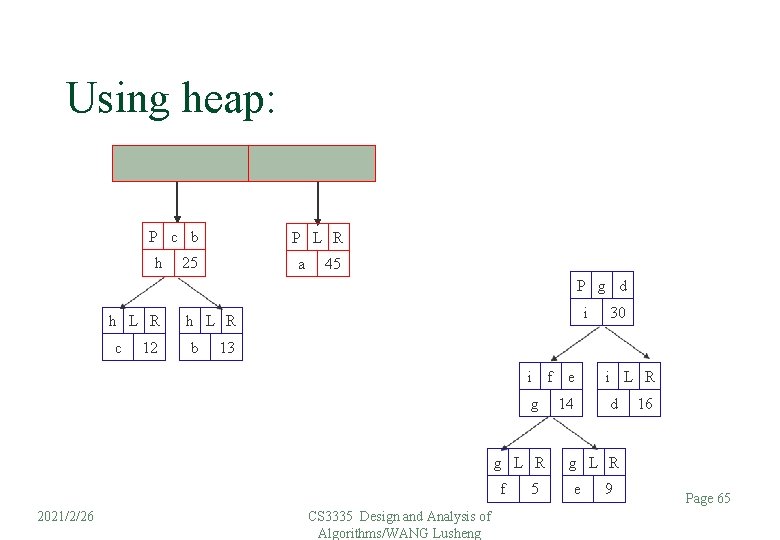
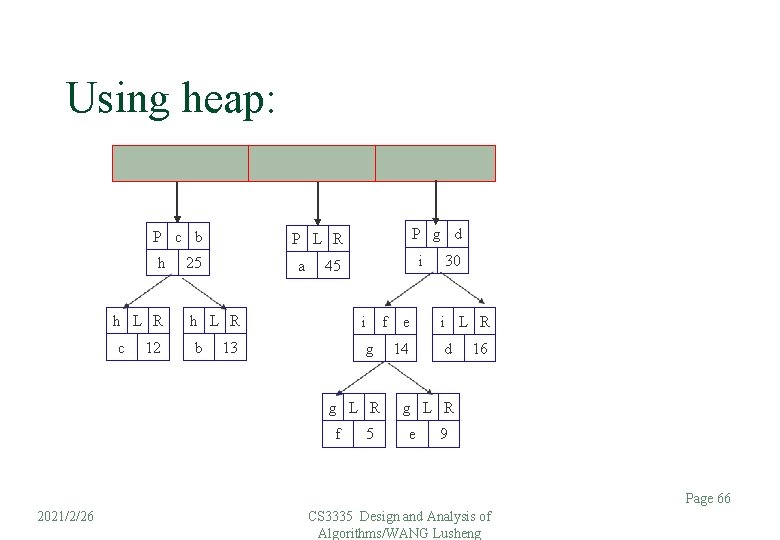
Using heap: P c b h P L R 25 a 45 P g d h L R c 12 i h L R b 13 i g g L R f 2021/2/26 30 CS 3335 Design and Analysis of Algorithms/WANG Lusheng 5 f e 14 i L R d 16 g L R e 9 Page 65

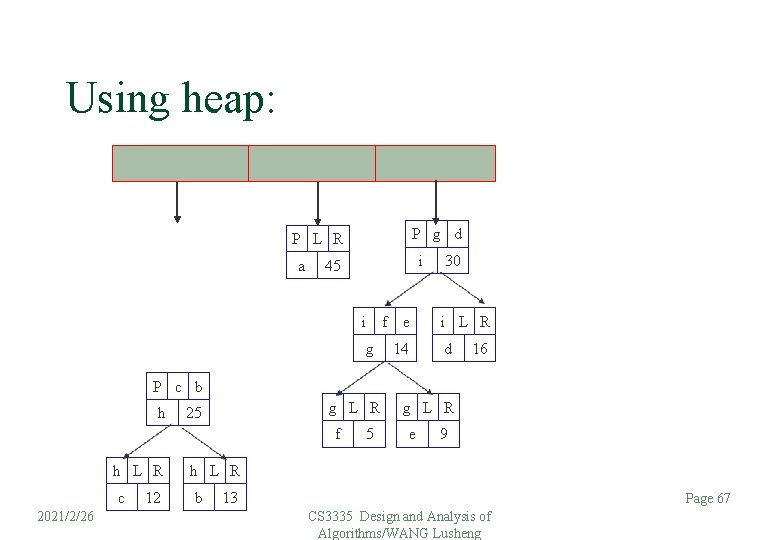
Using heap: P c b h h L R c 12 25 a i 45 h L R b P g d P L R i 13 g g L R f 5 f e 14 30 i L R d 16 g L R e 9 Page 66 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

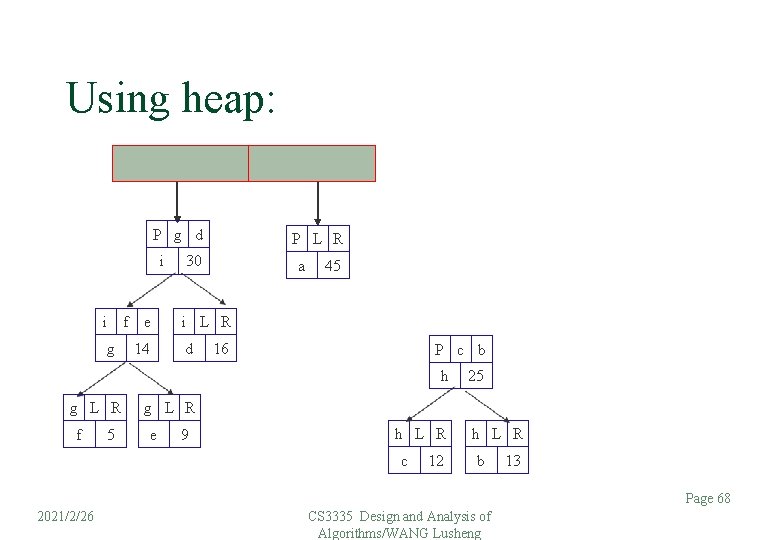
Using heap: P g d P L R a i 45 i g f e 14 30 i L R d 16 P c b h g L R 25 f h L R c 2021/2/26 12 5 g L R e 9 h L R b 13 Page 67 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

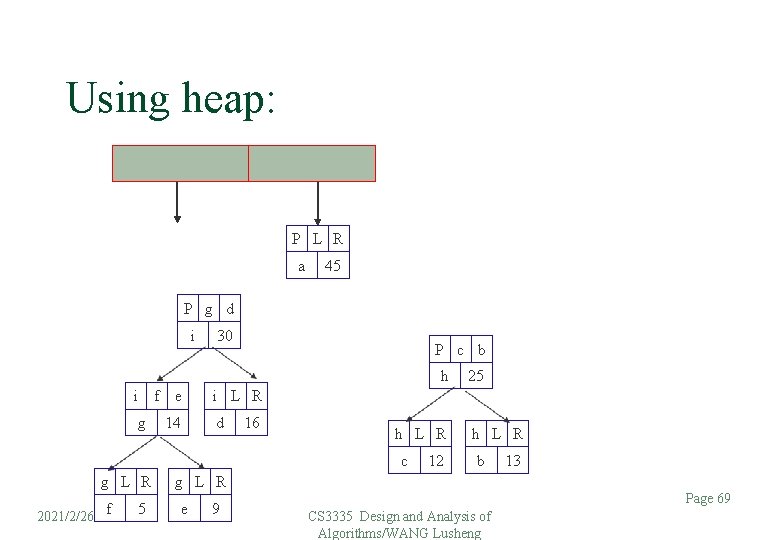
Using heap: P g d i i g f e 14 P L R 30 a 45 i L R d 16 P c b h g L R f 5 25 g L R e 9 h L R c 12 h L R b 13 Page 68 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

Using heap: P L R a 45 P g d i 30 P c b h i g f e 14 i L R d 16 h L R c g L R f 2021/2/26 5 25 12 h L R b g L R e 9 13 Page 69 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

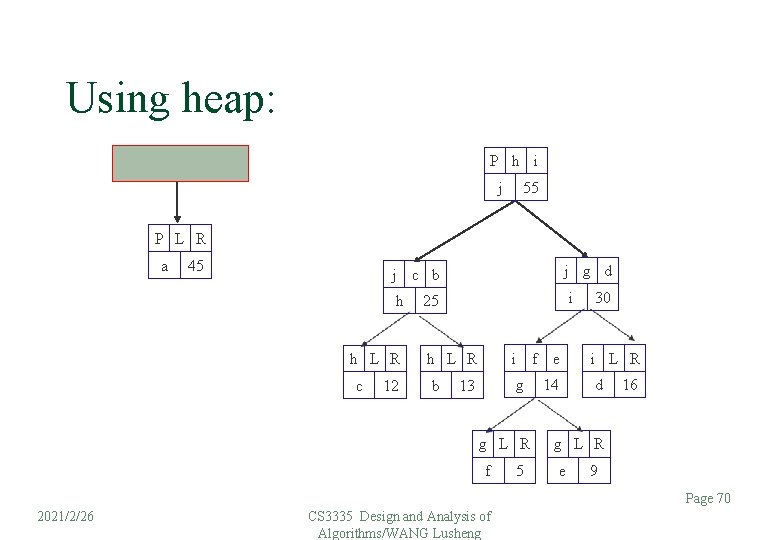
Using heap: P h i j 55 P L R a 45 j g d j c b h h L R c 12 i 25 i h L R b g 13 g L R f 5 f e 14 30 i L R d 16 g L R e 9 Page 70 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

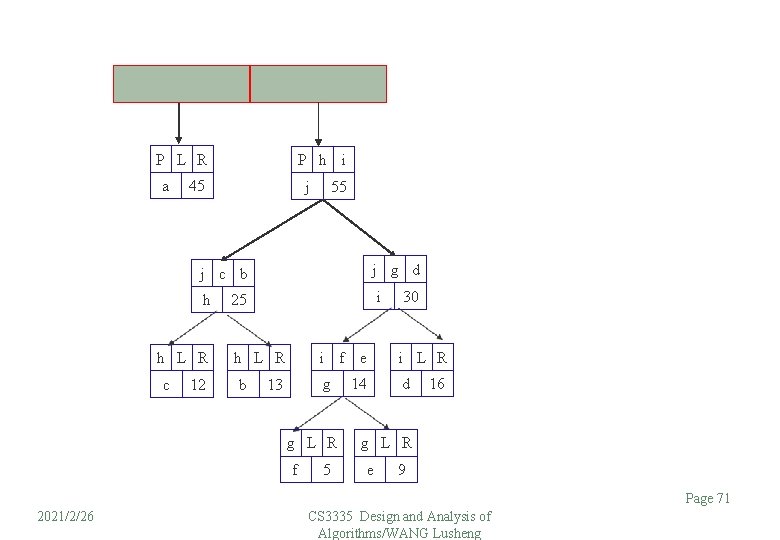
P L R a P h i 45 j 55 j g d j c b h h L R c 12 i 25 i h L R b g 13 g L R f 5 f e 14 30 i L R d 16 g L R e 9 Page 71 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

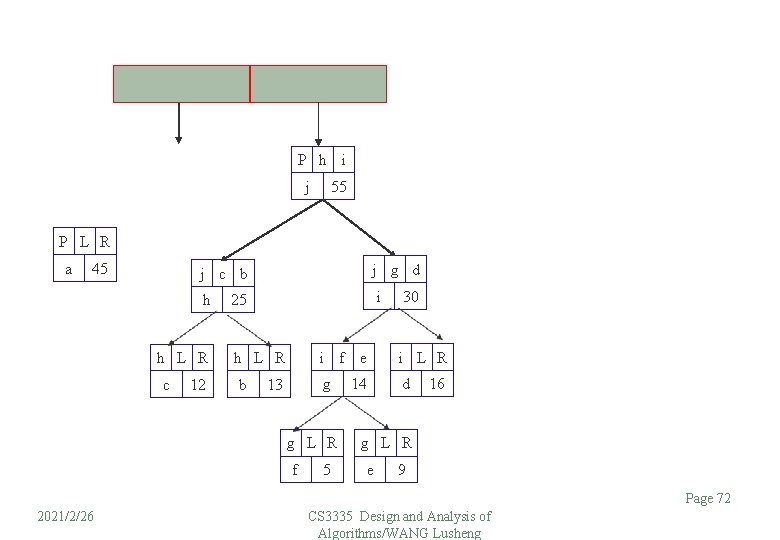
P h i j 55 P L R a 45 j g d j c b h h L R c 12 i 25 i h L R b g 13 g L R f 5 f e 14 30 i L R d 16 g L R e 9 Page 72 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

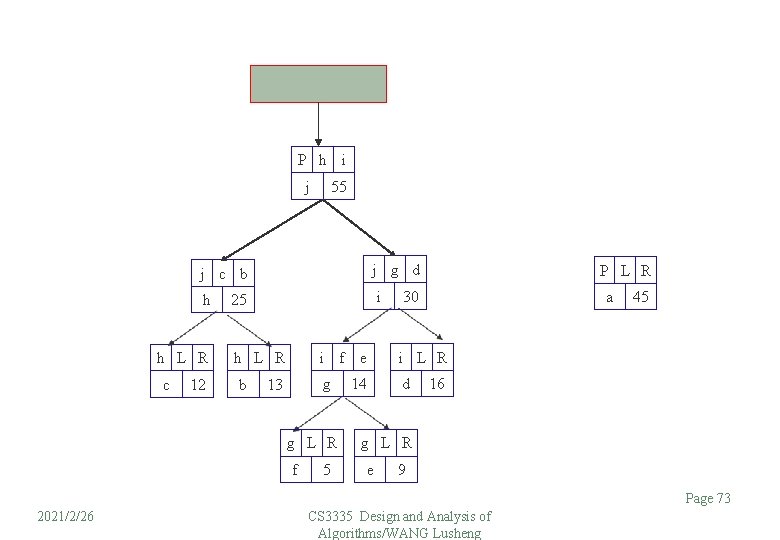
P h i j 55 j g d j c b h h L R c 12 i 25 i h L R b g 13 g L R f 5 f e 14 P L R 30 a 45 i L R d 16 g L R e 9 Page 73 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

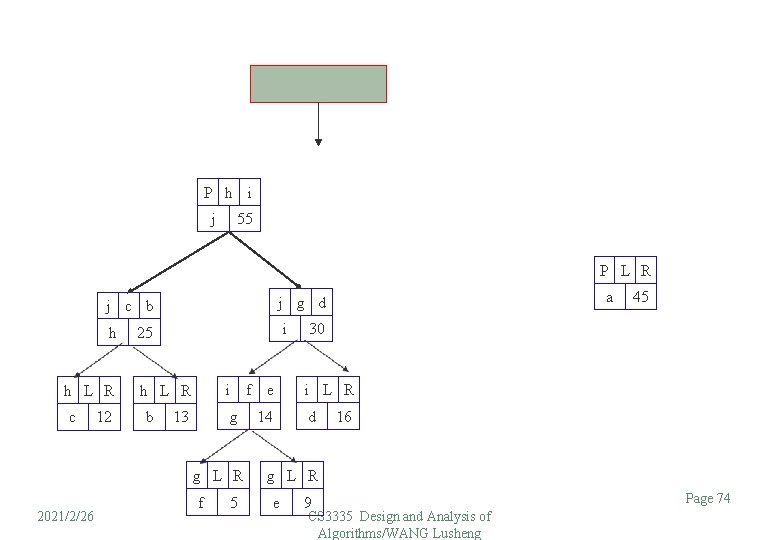
P h i j 55 P L R h h L R c 12 i 25 i h L R b g 13 g L R 2021/2/26 a j g d j c b f 5 f e 14 45 30 i L R d 16 g L R e 9 CS 3335 Design and Analysis of Algorithms/WANG Lusheng Page 74

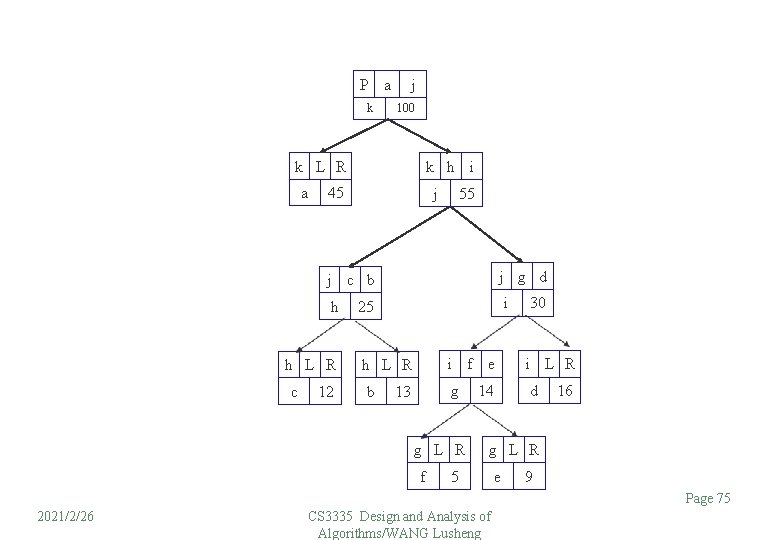
P a k j 100 k L R a k h i 45 j 55 j g d j c b h h L R c 12 i 25 i h L R b g 13 g L R f f e 14 30 i L R d 16 g L R 5 e 9 Page 75 2021/2/26 CS 3335 Design and Analysis of Algorithms/WANG Lusheng

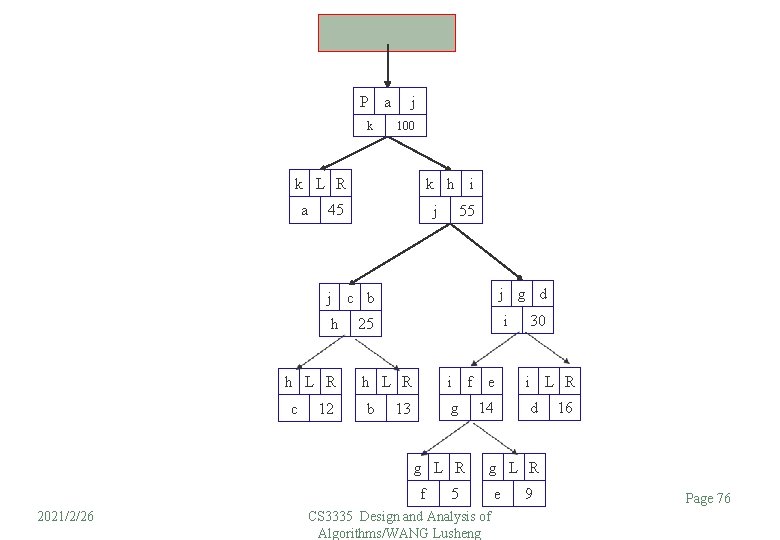
P a k j 100 k L R a k h i 45 j 55 j g d j c b h h L R c 12 i 25 i h L R b g 13 g L R f 2021/2/26 f e 14 30 i L R d 16 g L R 5 CS 3335 Design and Analysis of Algorithms/WANG Lusheng e 9 Page 76

Exercise Modify My. Heap. java in Tutorial 6’s folder so that the class Array. Node has five data fields: int key; char letter; Array. Node parent; Array. Node left; Array. Node right; and use the modified My. Heap to construct Huffman code tree. The program can read n pairs (ai, bi) from the keyboard , where ai is the number of times that character/letter bi appears and construct the Huffman code tree for the n pairs. Page 77 2021/2/26