Huffman Code Greedy Algorithm A R Hadaegh Dr

Huffman Code Greedy Algorithm A. R. Hadaegh Dr. Ahmad R. Hadaegh California State University San Marcos (CSUSM) Page 1

• Sometimes for security purpose we need to encode a text • One way to encode a text is to represent each character by a bit string • The number of times a particular character like “x” appears in a text is called frequency of the character. • The goal is to report the data using the minimum number of bits possible • In order to do this we need to compress the data • It is important to compress the data when large amounts o data are to be stored or tyransmitted • The most common way to represent a character is by using fixed-length bit string A. R. Hadaegh Dr. Ahmad R. Hadaegh California State University San Marcos (CSUSM) Page 2

• For example, ASCII (American Standard code for Information Interchange) represents each character by a string of 7 bits • Suppose we have a paragraph where • Space appears 60 times • ‘A’ appears 22 times • ‘O’ appears 16 times • ‘R’ appears 13 times • ‘S’ appears 6 times and • ‘T’ appears 4 times • If the ASCII code for these characters are • Space: 0100000 • ‘A’ : 1000001 • ‘O’: 1001111 • ‘R’ 1010010 • ‘S’: 1010011 • ‘T’: 1010100 • We are going to have • (60+22+16+13+6+4) =121 • 121* (7 bits) = 847 bits A. R. Hadaegh Dr. Ahmad R. Hadaegh California State University San Marcos (CSUSM) Page 3

• Huffman code provides alternative to ASCII and other fixed-length codes by using variable length bit string • It uses short-bit strings to represent the most frequently used character and to use longer bit strings to represent text in less space then if ASCII were used • The Huffman code sorts the character based on their frequency from lowest to highest and design bits tree structure. • First two character with lowest frequency are combined and the result is added to the pool of the numbers. Next the two lowest are selected and the result is added to the pool. This process continues until all numbers are combined and placed in the tree. • Then the path from the root to the number determined the bits assigned to represent the number A. R. Hadaegh Dr. Ahmad R. Hadaegh California State University San Marcos (CSUSM) Page 4

• For example, suppose the frequency of the characters in our paragraph are as follows: • • • Space: ‘A’ : ‘O’ : ‘R’ : ‘S’: ‘T’: 60 22 16 13 6 4 times times • The pool includes (60, 22, 16, 13, 6, and 4). So we take 6 and 4. 10 6 A. R. Hadaegh Dr. Ahmad R. Hadaegh 4 California State University San Marcos (CSUSM) Page 5

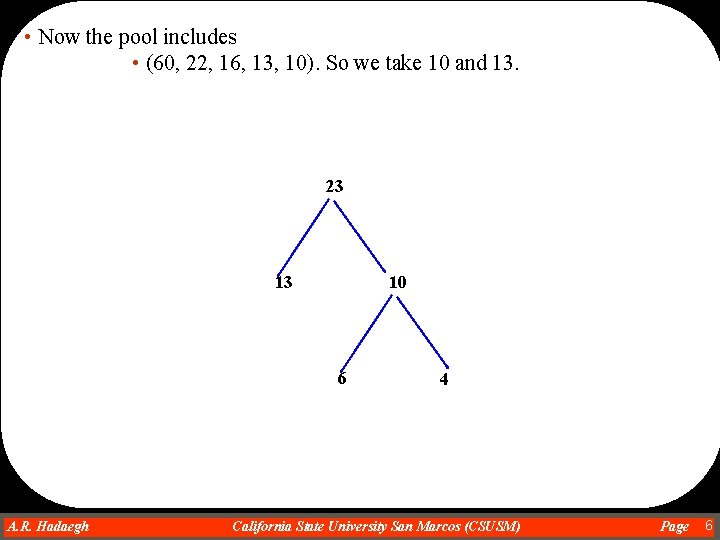
• Now the pool includes • (60, 22, 16, 13, 10). So we take 10 and 13. 23 10 13 6 A. R. Hadaegh Dr. Ahmad R. Hadaegh 4 California State University San Marcos (CSUSM) Page 6

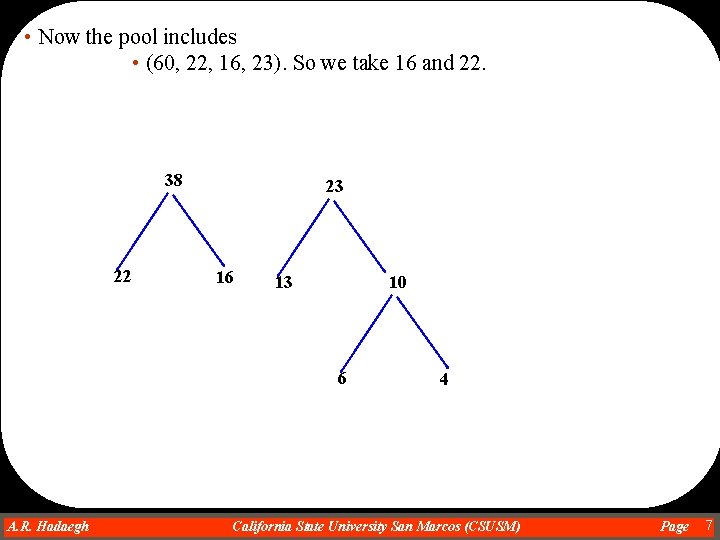
• Now the pool includes • (60, 22, 16, 23). So we take 16 and 22. 38 22 23 16 10 13 6 A. R. Hadaegh Dr. Ahmad R. Hadaegh 4 California State University San Marcos (CSUSM) Page 7

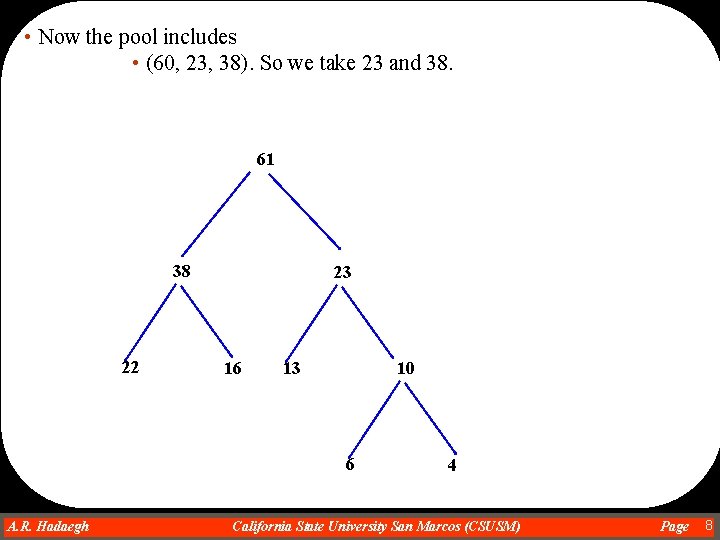
• Now the pool includes • (60, 23, 38). So we take 23 and 38. 61 38 22 23 16 10 13 6 A. R. Hadaegh Dr. Ahmad R. Hadaegh 4 California State University San Marcos (CSUSM) Page 8

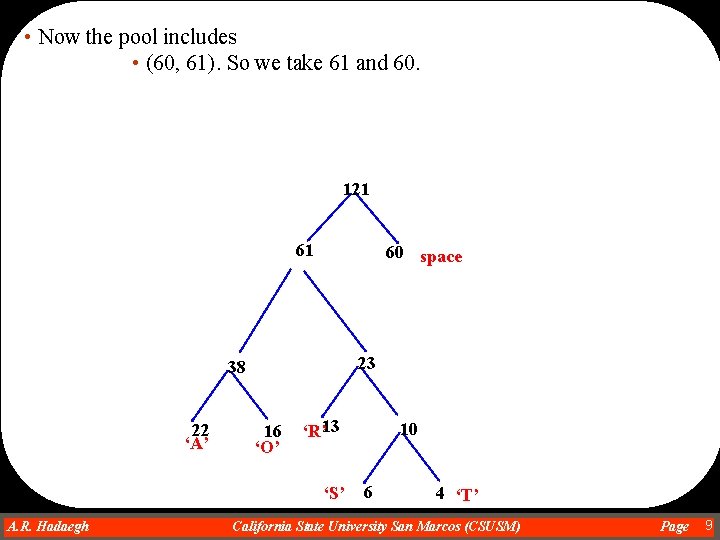
• Now the pool includes • (60, 61). So we take 61 and 60. 121 61 60 space 23 38 22 ‘A’ 16 ‘O’ ‘R’ 13 ‘S’ A. R. Hadaegh Dr. Ahmad R. Hadaegh 10 6 4 ‘T’ California State University San Marcos (CSUSM) Page 9

• Assign to the left and 0 to the right nodes and 0 1 space 1 1 ‘A’ 0 0 0 1 ‘O’ ‘R’ 1 ‘S’ 0 • Space: • ‘A’ : • ‘O’: • ‘R’ • ‘S’: • ‘T’: 0 111 110 101 1000 ‘T’ • The total bits used would be: • (60*1) + (22*3) + (16*3) + (13*3) + (6*4) + (4*4) = 253 A. R. Hadaegh Dr. Ahmad R. Hadaegh California State University San Marcos (CSUSM) Page 10