Hub Location Hub Network Design Spring School on

Hub Location & Hub Network Design Spring School on Supply Chain and Transportation Network Design HEC Montreal May 14, 2010 James F. Campbell College of Business Administration & Center for Transportation Studies University of Missouri-St. Louis, USA 1

Outline • Introduction, examples and background. • “Classic” hub location models. • Interesting “recent” research. I. Better solutions for classic models. II. More realistic and/or complex problems III. Dynamic hub location. IV. Models with stochasticity. V. Competition. VI. Data sets. • Conclusions. 2

Design a Network to Serve 32 Cities 32 demand points (origins and destinations) 32*31/2 = 496 direct connections 3
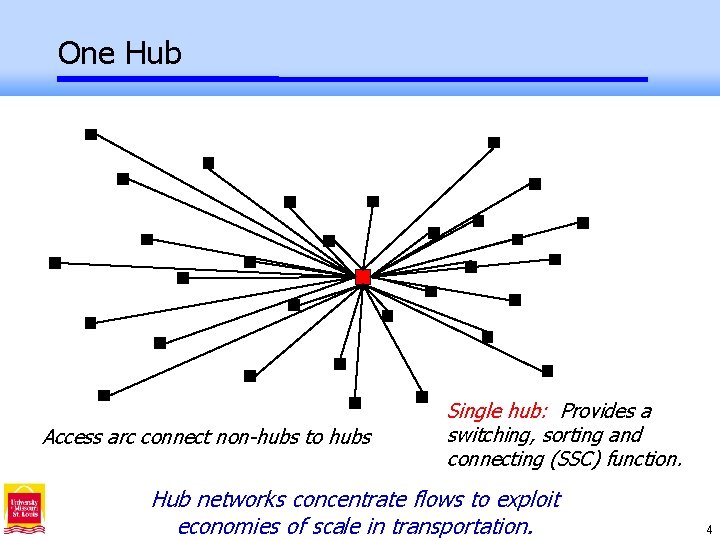
One Hub Access arc connect non-hubs to hubs Single hub: Provides a switching, sorting and connecting (SSC) function. Hub networks concentrate flows to exploit economies of scale in transportation. 4
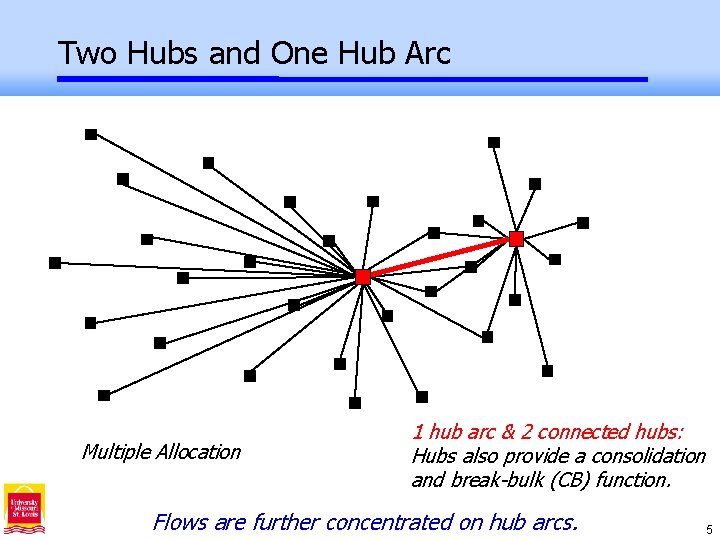
Two Hubs and One Hub Arc Multiple Allocation 1 hub arc & 2 connected hubs: Hubs also provide a consolidation and break-bulk (CB) function. Flows are further concentrated on hub arcs. 5
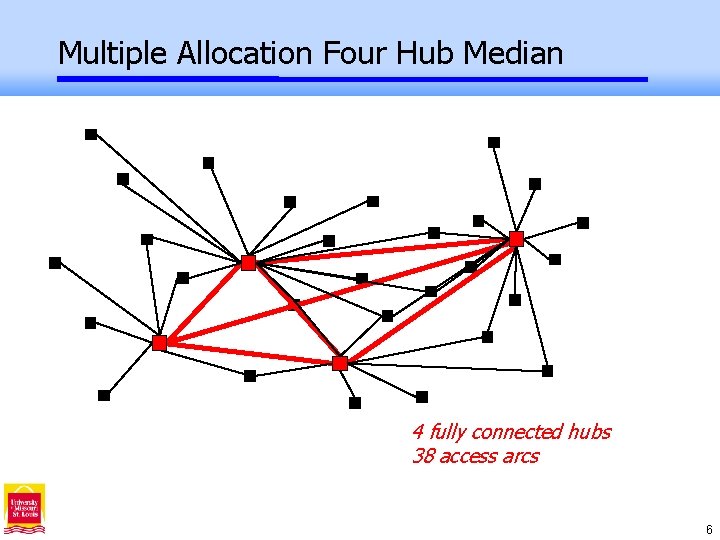
Multiple Allocation Four Hub Median 4 fully connected hubs 38 access arcs 6
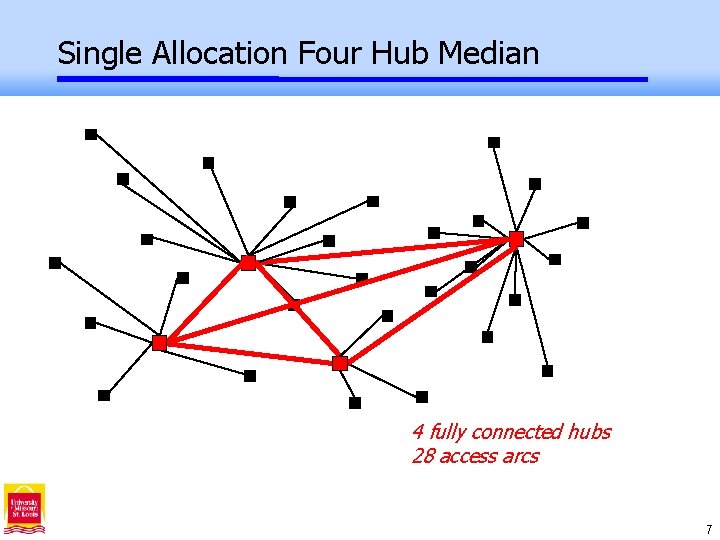
Single Allocation Four Hub Median 4 fully connected hubs 28 access arcs 7

Multiple Hubs and Hub Arcs 8
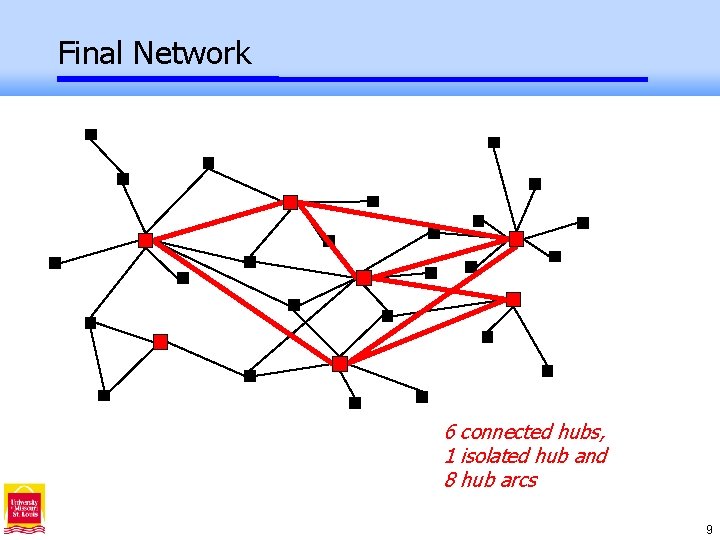
Final Network 6 connected hubs, 1 isolated hub and 8 hub arcs 9

Hub Networks • Allow efficient “many-to-many” transportation: - Require fewer arcs and concentrate flows to exploit transportation economies of scale. dis tri b ut ion • Hub arcs provide reduced cost transportation between two hubs (usually with larger vehicles). - Cost: i k m j : Cijkm = cik + ckm + cmj j - Distance: i k m j = dik + dkm + dmj i transfer collection • Hub nodes provide: m k - Sorting, switching and connection. - Consolidation/break-bulk to access reduced cost hub arcs. 10

Hub Location Applications • Passenger and Freight Airlines: - Hubs are consolidation airports and/or sorting centers. - Non-hubs are feeder airports. • Trucking: - LTL hubs are consolidation/break-bulk terminals. - Truckload hubs are relay points to change drivers/tractors. - Non-hubs are end-of-line terminals. • Postal operations: - Hubs are sorting centers; non-hubs are regional post offices. • Public transit: - Hubs are subway/light-rail stations. - Non-hubs are bus stations or patron o/d’s. • Computer & telecom networks. 11

Hub Location Motivation • Deregulation of transportation in USA: - Airlines (1978). - Trucking (1980). • Express delivery industry (Federal Express began in 1973). - Federal Express experiences: • Developed ILP models in ~1978 to evaluate 1 super-hub vs. 4 hubs. • Used OR models in mid-1970 s to evaluate adding “bypass hubs” to handle increasing demand. • Large telecommunications networks. 12

Hub Location Research • Strategic location of hubs and design of hub networks. - Not service network design, telecom, or continuous location research. • Began in 1980’s in diverse fields: - Geography, Transportation, OR/MS, Location theory, Telecommunications, Network design, Regional science, Spatial interaction theory, etc. • Builds on developments in “regular” facility location modeling. 13

Hub Location Foundations • First hub publications: Morton O’Kelly (1985 -1987): - Transportation Science, Geographical Analysis, EJOR: • First math formulation (quadratic IP). • 2 simple heuristics for locating 2 -4 hubs with CAB data set. - Focus on single allocation and schedule delay. • Continuous approximation models for many-tomany transportation. - Built on work with GM by Daganzo, Newell, Hall, Burns, etc. in 1980 s. - Daganzo, 1987, “The break-bulk role terminals in many-to -many logistics networks”, Operations Research. • Considered origin-hub-destination, but without discounted inter-hub transportation. 14

Hub Location & Network Design Given: - Network G=(V, E) - Set of origin-destination flows, Wij - Discount factor for hub arcs, 0< <1 Design a minimum cost network with hub nodes and hub arcs to satisfy demand Wij. Select hub nodes and hub arcs. Assign each non-hub node to hubs. 15

Traditional Discrete Location Models • Demand occurs at discrete points. • Demand points are assigned to the closest (least cost) facility. • Objective is related to the distance or cost between the facilities and demand points. • “Classic” problems: - p-median (p. MP): Minimize the total transportation cost (demand weighted total distance). - Uncapacitated facility location problem (UFLP): Minimize the sum of fixed facility and transportation costs. - p-center: Minimize the maximum distance to a customer. - Set Covering: Minimize the # of facilities to cover all customers. - Maximum covering: Maximize the covered demand for a given number of facilities (or given budget). 16

Discrete Hub Location Models • Demand is flows between origins and destinations. • Non-hubs can be allocated to multiple hubs. • Objective is usually related to the distance or cost for flows (origin-hub-destination). - Usually, all flows are routed via at least one hub. • Analogous “classic” hub problems: - p-hub median (p. MP): Minimize the total transportation cost (demand weighted total distance). - Uncapacitated hub location problem (UHLP): Minimize the sum of fixed hub and transportation costs. - p-hub center: Minimize the maximum distance to a customer. - Hub Covering: Minimize the # of hubs to cover all customers. - Maximum covering: Maximize the covered demand for a given number of hubs (or given budget). 17

Hub Location Research • Very rich source of problems - theoretical and practical. • Problems are hard!! • A wide range of exact and heuristic solution approaches are in use. • Many extensions: Capacities, fixed costs for hubs and arcs, congestion, hierarchies, inter-hub and access network topologies, competition, etc. • Many areas still awaiting good research. 18

Hub Location Literature • Early hub location surveys/reviews: - Campbell, 1994, Studies in Locational Analysis. Ø 23 transportation and 9 telecom references. - O’Kelly and Miller, 1994, Journal of Transport Geography. - Campbell, 1994, “Integer programming formulations of discrete hub location problems”, EJOR. - Klincewicz, 1998, Location Science. • Recent surveys: - Campbell, Ernst and Krishnamoorthy, 2002, in Facility Location: Applications and Theory. - Alumur and Kara, 2008, EJOR (106 references). - Computers & Operations Research , 2009, vol. 36. • Much recent and current research… 19
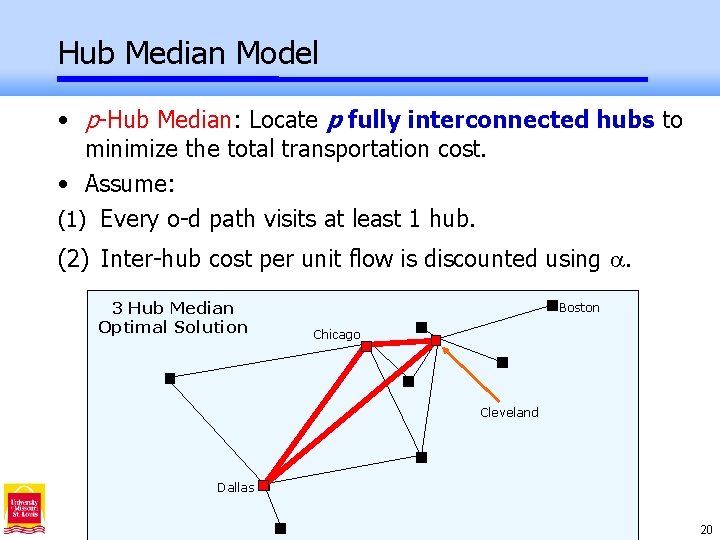
Hub Median Model • p-Hub Median: Locate p fully interconnected hubs to minimize the total transportation cost. • Assume: (1) Every o-d path visits at least 1 hub. (2) Inter-hub cost per unit flow is discounted using . 3 Hub Median Optimal Solution Boston Chicago Cleveland Dallas 20

Hub Median Formulations • Cost: i k m j : χcik + ckm + δcmj • Single allocation: i n collection transfer k utio b i tr dis j m Zik= 1 if node i is allocated to a hub at k ; 0 otherwise Zkk= 1 if node k is a hub; 0 otherwise Min Subject to Link flows and hubs Serve all o-d flows Use p hubs 21

Hub Median Formulations • Multiple allocation: 4 subscripted “path” variables Xijkm= fraction of flow that travels i-k-m-j Hk = 1 if node k is a hub; 0 otherwise Cost: i k m j : Cijkm = χcik + ckm + δcmj Min Subject to Serve all o-d flows Use p hubs Link flows & hubs 22

Hub Median Formulations • Multiple allocation: 3 subscripted “flow” variables i collection Zik transfer k Y ikm n utio b i tr dis m X imj j Zik= flow from origin i to hub k Y ikm= flow originating at i from hub k to hub m X imj= flow originating at i from hub m to destination j Min 23

Hub Median Formulations • Multiple allocation – 3 subscripted “flow” variables Min Subject to Serve all o-d flows Use p hubs Flow balance Link flows & hubs 24

Hub Center and Hub Covering • Introduced as analogues of “regular” facility center and covering problems…but notion of covering is different. • Campbell (EJOR 1994) provided 3 types of centers/covering: - Maximum cost/distance for any o-d pair - Maximum cost /distance for any single link in an o-d path. - Maximum cost/distance between an o/d and a hub. i collection transfer k n utio b i r t dis j m • Much recent attention: - Ernst, Hamacher, Jiang, Krishnamoorthy, and Woeginger, 2009, “Uncapacitated single and multiple allocation p-hub center problems”, Computers & OR 25

Hub Center Formulation • Xik = 1 if node i is allocated to hub k, and 0 otherwise • Xkk = 1 node k is a hub z is the maximum transportation cost between all o–d pairs. rk = “radius” of hub k (maximum distance/cost between hub k and the nodes allocated to it). Min Subject to Serve all o-d flows Link flows & hubs Use p hubs Hub radius Objective k 26

Hub Location Themes I. Better solution algorithms for “classic” problems. II. More realistic and/or complex problems. - More general topologies for inter-hub network and access network. - Objectives with cost + service. - Other: multiple capacities, bicriteria models, etc. III. Dynamic hub location. IV. Models with stochasticity. V. Competition. VI. Data sets. 27

I. Better solutions for “classic” problems • Improved formulations lead to better solutions and solving larger problems… Ø Hamacher, Labbé, Nickel, and Sonneborn, 2004 “Adapting polyhedral properties from facility to hub location problems”, Discrete Applied Mathematics. Ø Marín, Cánovas, and Landete, 2006, “New formulations for the uncapacitated multiple allocation hub location problem”, EJOR. - Uses preprocessing and polyhedral results to develop tighter formulations. - Compares several formulations. 28

Better solutions for “classic” problems • Contreras, Cordeau, and Laporte, 2010, “Benders decomposition for large-scale uncapacitated hub location”. - Exact, sophisticated solution algorithm for UMAHLP. - Solves very large problems with up to 500 nodes (250, 000 commodities). - ~2/3 solved to optimality in average ~8. 6 hours. • Contreras, Díaz, and Fernández, 2010, “Branch and price for large scale capacitated hub location problems with single assignment”, INFORMS Journal on Computing. - Single allocation capacitated hub location problem. - Solves largest problems to date to optimality (200 nodes) up to 12. 5 hrs. - Lagrangean relaxation and column generation and branch and price. 29

II. More Realistic and/or Complex Problems • More general topologies for inter-hub network and access network. - Inter-hub network: Trees, incomplete hub networks, isolated hubs, etc. - Access network: “Stopovers”, “feeders”, routes, etc. • Better handling of economies of scale. - Flow dependent discounts, flow thresholds, etc. - Restricted inter-hub networks. • Objectives with cost + service. • Others: multiple capacities, bicriteria models, etc. 30

Weaknesses of “Classic” Hub Models • Hub center and hub covering models: - Not well motivated by real-world systems. - Ignore costs: Discounting travel distance or time while ignoring costs seems “odd”. • Hub median (and UHLP) models: - Assume fully interconnected hubs. - Assume a flow-independent cost discount on all hub arcs. - Ignore travel times and distances. 31

Hub Median Model • p-Hub Median: Locate p fully interconnected hubs to minimize the total transportation cost. - Hub median and related models do not accurately model economies of scale. - All hub-hub flows are discounted (even if small) and no access arc flows are discounted (even if large)! 3 Hub Median Optimal Solution 23 Chicago 94 305 217 5 Boston 120 76 85 Cleveland Dallas 166 low flows on hub arcs 32

Better Handling of Economies of Scale • Flow dependent discounts: Approximate a non-linear discounts by a piece-wise linear concave function. - O’Kelly and Bryan, 1998, Trans. Res. B. - Bryan, 1998, Geographical Analysis. - Kimms, 2006, Perspectives on Operations Research. • More general topologies for inter-hub network and access network - “Tree of hubs”: Contreras, Fernández and Marín, 2010, EJOR. - “Incomplete” hub networks: Alumur and Kara, 2009, Transportation Research B - Hub arc models: Campbell, Ernst, and Krishnamoorthy, 2005, Management Science. 33

Hub Arc Model • Hub arc perspective: Locate q hub arcs rather than p fully connected hub nodes. - Endpoints of hub arcs are hub nodes. • Hub Arc Location Problem: Locate q hub arcs to minimize the total transportation cost. Ø q hub arcs and ≤ 2 q hubs. Ø Assume as in the hub median model that: • Every o-d path visits at least 1 hub. • Cost per unit flow is discounted on q hub arcs using . • Each path has at most 3 arcs and one hub arc (origin-hubhub-destination): model HAL 1. 34
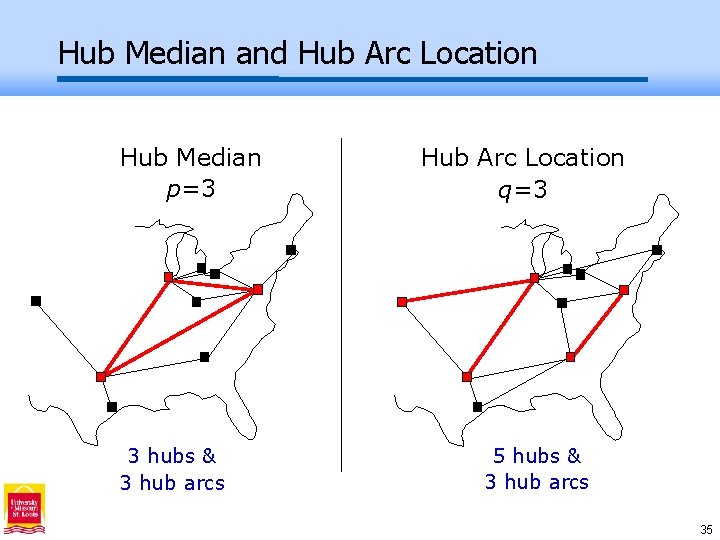
Hub Median and Hub Arc Location Hub Median p=3 3 hubs & 3 hub arcs Hub Arc Location q=3 5 hubs & 3 hub arcs 35

Time Definite Hub Arc Location • Combine service level (travel time) constraints with cost minimization to model time definite transportation. • Motivation: Time definite trucking: - 1 to 4 day very reliable scheduled service between terminals. - Air freight service by truck! Dest ATL JFK MIA ORD SEA • Transit Distance Days 575 2 982 2 1230 3 308 1 2087 4 Drop-off at STL 22: 00 22: 00 Pickup at Dest 7: 00 9: 00 8: 30 Campbell, 2009, “Hub location for time definite transportation”, Computers & OR. 36

Service Levels • Limit the travel distance via the hub network to ensure the schedule (high service level) can be met with ground transport. Direct o-d Distance 0 - 400 miles 400 - 1000 miles 1000 - 1800 miles High Service Level Max Travel Distance 600 miles 1200 miles 2000 miles • Problems with High service levels (High SL) have reduced sizes, since long paths are not feasible. • Formulate as MIP and solve via CPLEX 10. 1. 1. 37
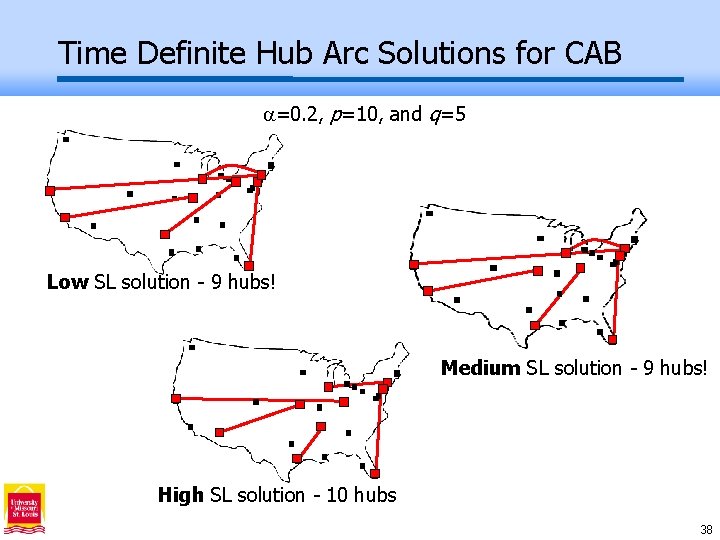
Time Definite Hub Arc Solutions for CAB =0. 2, p=10, and q=5 Low SL solution - 9 hubs! Medium SL solution - 9 hubs! High SL solution - 10 hubs 38
Time Definite Hub Locations • High service levels make problems “easier”. • High service levels “force” some hub locations. • Good hub cities: - Large origins and destinations. • Chicago, New York, Los Angeles. - Large isolated cities near the perimeter. • Miami, Seattle. - Some centrally located cities. • Kansas City, Cleveland. • Poor hub cities: - Medium or small cities near large origins & destinations. • Tampa. 39

Models with Congestion Ø Elhedhli and Wu, 2010, “A Lagrangean heuristic for huband-spoke system design with capacity selection and congestion”, INFORMS Journal on Computing. - Single allocation. - Minimize sum of transportation cost, fixed cost and congestion “cost”. - Congestion at hub k: - Uses multiple capacity levels. - Solves small problems up to 4 hubs and 25 nodes to within 1% of optimality. 40

Another Model with Congestion Ø Koksalan and Soylu, 2010, “Bicriteria p-hub location problems and evolutionary algorithms”, INFORMS Journal on Computing. - Two multiple allocation bicriteria uncapacitated p-HMP models. • Model 1: Minimize total transportation cost and minimize total collection and distribution cost. • Model 2: Minimize total transportation cost and minimize maximum delay at a hub. - Delay (congestion) at hub k: - Solves with “favorable weight based evolutionary algorithm”. 41

III. Dynamic Hub Location How should a hub network respond to changing demand? ? Ø Contreras, Cordeau, Laporte, 2010, “The dynamic hub location problem”, Transportation Science. - Multiple allocation, fully interconnected hubs. - Dynamic (multi-period) uncapacitated hub location with up to 10 time periods. - In each period, adds new o-d pairs (commodities) and increase or decrease the flow for existing o-d pairs. - Hubs can be added, relocated or removed. - Solves up to 100 nodes and 10 time periods with branch and bound with Langrangean relaxation. 42
Isolated Hubs • Isolated hubs are not endpoints of hub arcs. - Provide only a switching, sorting, connecting function; not a consolidation/break-bulk function. - Give flexibility to respond to expanding demand with incremental steps. • How can isolated hubs be used, especially in response to increasing demand in a fixed region and demand in an expanding region. Ø Campbell, 2010, “Designing Hub Networks with Connected and Isolated Hubs”, HICSS 43 presentation. 43
Hub Arc Location with Isolated Hubs • Locate q hub arcs with p hubs to minimize the total transportation cost. Ø If p>2 q there will be isolated hubs; When p 2 q isolated hubs may provide lower costs. Ø Each non-hub is connected to one or more hubs. Key assumptions: 1. Every o-d path visits at least 1 hub. 2. Hub arc cost per unit flow is discounted using . 3. Each path has at most 3 arcs and one hub arc: origin-hub-destination. Cost: i-k-m-j = 44
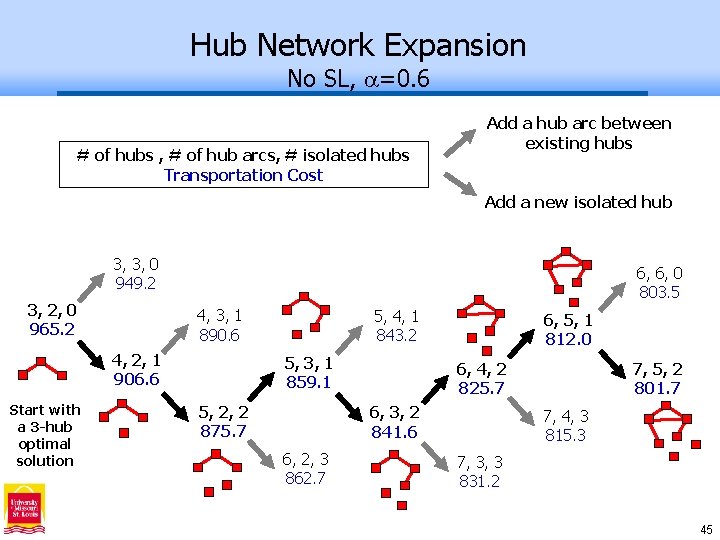
Hub Network Expansion No SL, =0. 6 # of hubs , # of hub arcs, # isolated hubs Transportation Cost Add a hub arc between existing hubs Add a new isolated hub 3, 3, 0 949. 2 3, 2, 0 965. 2 6, 6, 0 803. 5 4, 3, 1 890. 6 4, 2, 1 906. 6 Start with a 3 -hub optimal solution 5, 4, 1 843. 2 5, 3, 1 859. 1 5, 2, 2 875. 7 6, 5, 1 812. 0 6, 4, 2 825. 7 6, 3, 2 841. 6 6, 2, 3 862. 7 7, 5, 2 801. 7 7, 4, 3 815. 3 7, 3, 3 831. 2 45

Geographic Expansion q=3 hub arcs Optimal with no west-coast cities, p=4 Add 5 West. Coast cities Allow 1 Isolated Hub 1 isolated hub, Cost=914 No isolated hubs, Cost=1085 Allow hub arcs to be moved 1 isolated hub, Cost=864 46

Findings for Isolated Hubs • Isolated hubs are useful to respond efficiently to: - an expanding service region and - an increasing intensity of demand. • Adding isolated hubs may be a more cost effective than adding connected hubs (and hub arcs). • Isolated hubs seem most useful in networks having: few hub arcs, small values (more incentive for consolidation), and/or high service levels. • With expansion, the same hubs are often optimal – but the roles change from isolated to connected. 47

IV. Models with Stochasticity How should stochasticity be incorporated? ? Ø Lium, Crainic and Wallace, 2009, “A study of demand stochasticity in service network design, Transportation Science. - Does not assume particular topology and shows hub-and-spoke structures arise due to uncertainty. “consolidation in hub-and-spoke networks takes place not necessarily because of economy of scale or other similar volume-related reasons, but as a result of the need to hedge against uncertainty” Ø Sim, Lowe and Thomas, 2009, “The stochastic p-hub center problem with service-level constraint”, Computers & OR. - Single assignment hub covering where the travel time Tij is normally distributed with a given mean and standard deviation. - Locate p hubs to minimize so that the probability is at least that the total travel time along the path i→k→l→j is at most . 48

V. Competitive Hub Location • Suppose two firms develop hub networks to compete for customers. • Sequential location - Maximum capture problem: - Marianov, Serra and Re. Velle, 1999, “Location of hubs in a competitive environment”, EJOR. - Eiselt and Marianov, 2009, “A conditional p-hub location problem with attraction functions”, Computers & OR. • Stackelberg hub problems: - Sasaki and Fukushima, 2001, “Stackelberg hub location problem”, Journal of Operations Research Society of Japan. - Sasaki, 2005, “Hub network design model in a competitive environment with flow threshold”, Journal of Operations Research Society of Japan. 49

Stackelberg Hub Arc Location • Use revenue maximizing hub arc models with Stackelberg competition. • Two competitors (a leader and follower) in a market. - The leader first optimally locates its own q. A hub arcs, knowing that the follower will later locate its own hub arcs. - The follower optimally locates its own q. B hub arcs after the leader, knowing the leader’s hub arc locations. • Assume: - Competitors cannot share hubs. - Customers travel via the lowest cost path in each network. • The objective is to find an optimal solution for the leader given the follower will subsequently design its optimal hub arc network. 50

How to Allocate Customers among Competitors? • Customers are allocated between competitors based on the service disutility, which may depend on many factors: - Fares/rates, travel times, departure and arrival times, frequencies, customer loyalty programs, etc. • For a strategic location model, we assume revenues (fares/rates) are the same for each competitor. • We focus on disutility measures in terms of travel distance (time) and travel cost. • Key factors may differ between passenger and freight transportation. 51

Cost & Service • For freight, a shipper does not care about the path as long as the freight arrives “on time”. - Often pick up at end of day and deliver at the beginning of a future day. - Allocate between competitors based on relative cost of service. • Passengers are more sensitive to the total travel time (though longer trips allow more circuity). - Allocate between competitors based on relative service (travel time or distance). 52

Distance Ratio and Cost Ratio Distance ratio (passengers): Dij. A: The distance for the trip from i to j that achieves the minimum cost for Firm A. Dij. B : The distance for the trip from i to j that achieves the minimum cost for Firm B. j DRij =(Dij. A–Dij. B) /(Dij. A +Dij. B) i k l Cost ratio (freight): Cij. A : The minimum cost for the trip from i to j for Firm A. Cij. B : The minimum cost for the trip from i to j for Firm B. CRij =(Cij. A–Cij. B) /(Cij. A +Cij. B) As Dij. A (or Cij. A) 0, DRij (or CRij) -1, and Firm A captures all revenue. 53

5 -level Step Function for Customer Allocation Fraction of demand captured by Firm A Φij. A(x. A, x. B) = fraction of demand captured by Firm A CRij or Drij –r 1 to –r 2 to r 1 > r 1 Φij. A(x. A, x. B) 100% 75% 50% 25% 0% r 1 and r 2 determine selectivity level of customers. r 1 = r 2 = 0 is an “all-or-nothing” allocation. r 1 = 0. 75, r 2 = 0. 50 is insensitive to differences. 54

Notation • Given: - V = set of demand nodes, V (|V |=n) Wij = set of origin-destination flows Fij = set of origin-destination revenues (e. g. airfares) dij = distance between i and j Cijkl = unit cost for the path i k l j = dik+ dkl+dlj s = cost discount factor for hub arcs, 0< ≤ 1. • Decision variables: i k l j - xijkl. A (xijkl. B) = flow for i k l j for Firm A (B) - ykl. A (ykl. B) = 1 if there is a hub arc k–l for Firm A (B) - zk. A (zk. B) = 1 if there is a hub at city k for Firm A (B) 55
HALCE-B (Firm B’s problem) Maximize B’s total revenue Hub arcs & hubs Network Flow 56

HALCE-A (Firm A’s Problem) Maximize A’s total revenue Hub arcs & hubs Network Flow Firm B finds an optimal solution 57

Optimal Solution Algorithm • “Smart” enumeration algorithm: Ø Enumerate all of Firm A’s sets of q. A hub arcs. Ø For each set of Firm A’s hub arcs, use bounding tests to enumerate only some of Firm B’s q. B hub arcs and only some OD pairs. • Bounding tests are effective and allow problems with up to 3 hub arcs for Firm A and Firm B to be solved to optimality. • But we would still like to solve larger problems… 58
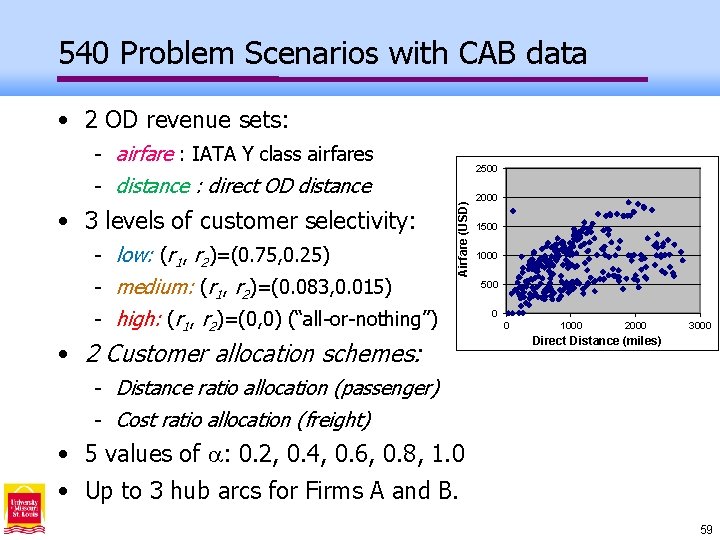
540 Problem Scenarios with CAB data • 2 OD revenue sets: - airfare : IATA Y class airfares 2500 • 3 levels of customer selectivity: - low: (r 1, r 2)=(0. 75, 0. 25) - medium: (r 1, r 2)=(0. 083, 0. 015) Airfare (USD) - distance : direct OD distance - high: (r 1, r 2)=(0, 0) (“all-or-nothing”) • 2 Customer allocation schemes: 2000 1500 1000 500 0 0 1000 2000 3000 Direct Distance (miles) - Distance ratio allocation (passenger) - Cost ratio allocation (freight) • 5 values of : 0. 2, 0. 4, 0. 6, 0. 8, 1. 0 • Up to 3 hub arcs for Firms A and B. 59

Results: High Customer Selectivity Distance ratio allocation q. A=q. B=2, =0. 6 Revenue = airfare Revenue = distance Red lines: Firm A’s optimal solution Blue lines: Firm B’s optimal solution 60
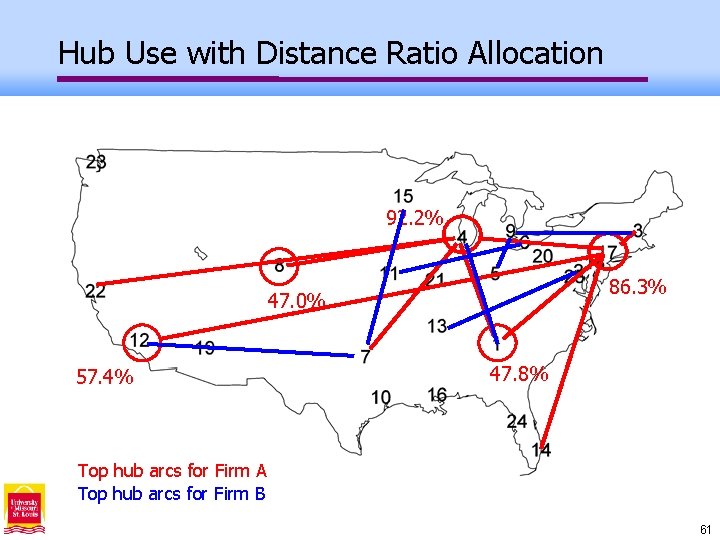
Hub Use with Distance Ratio Allocation 92. 2% 86. 3% 47. 0% 57. 4% 47. 8% Top hub arcs for Firm A Top hub arcs for Firm B 61
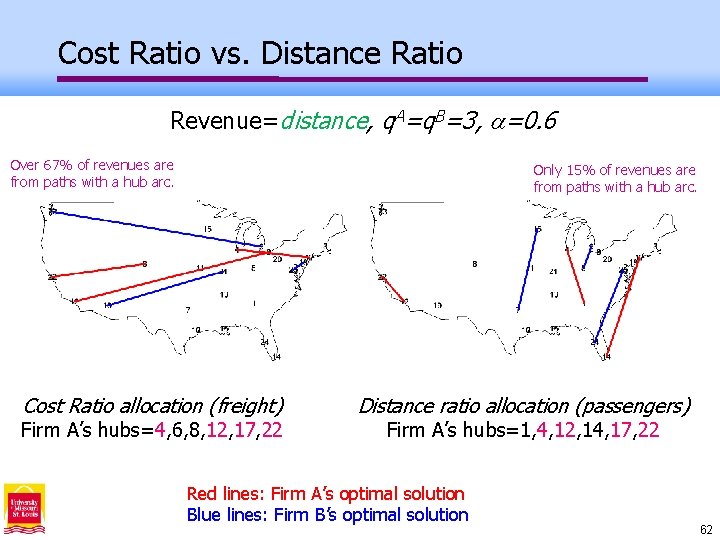
Cost Ratio vs. Distance Ratio Revenue=distance, q. A=q. B=3, =0. 6 Over 67% of revenues are from paths with a hub arc. Only 15% of revenues are from paths with a hub arc. Cost Ratio allocation (freight) Firm A’s hubs=4, 6, 8, 12, 17, 22 Distance ratio allocation (passengers) Firm A’s hubs=1, 4, 12, 14, 17, 22 Red lines: Firm A’s optimal solution Blue lines: Firm B’s optimal solution 62

Findings • The leader (Firm A) usually has an advantage, but not always (“first entry paradox”). • Distance ratio allocation encourages one-stop routes (as preferred by passengers). • Cost ratio allocation encourages more circuitous twostop routes (as in freight transportation). • Large origins/destinations have a large advantage for hub location. - Peripheral cities have a geographic disadvantage for hub location. • Though the optimal hub arcs vary considerably, the competitors generally use the same optimal hub nodes. 63

Competitive Model Conclusions • There are some interesting differences between the leader’s and follower’s strategies: - The leader tends to use fewer hubs more intensively, but the follower performs about as well in many cases! - The leader tends to capture the higher revenue customers, while the follower captures more, but less valuable, customers. • Optimal network design can be very sensitive to the customer allocation mechanisms. 64

VI. Hub Location Data Sets • Much work has been done with only a few data sets: - CAB 25: 25 cities in US. - AP: up to 200 postal locations in Sydney, Australia. - “Turkish data”: 81 nodes in Turkey • What should alpha be? 65
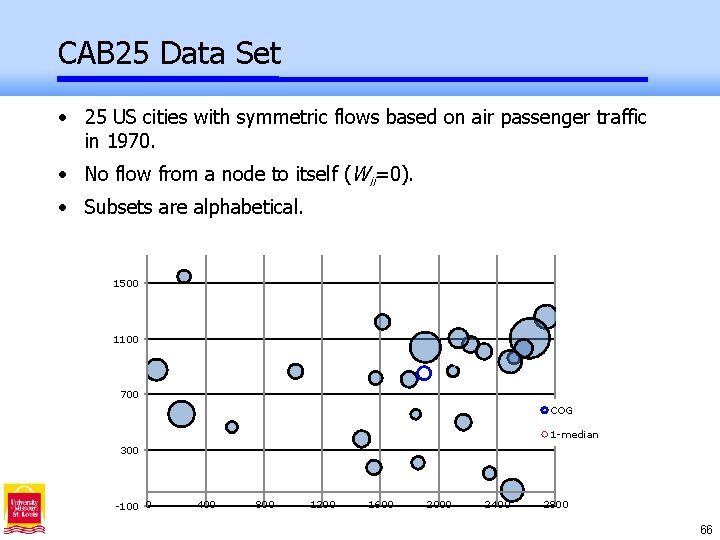
CAB 25 Data Set • 25 US cities with symmetric flows based on air passenger traffic in 1970. • No flow from a node to itself (Wii=0). • Subsets are alphabetical. 1500 1100 700 COG 1 -median 300 -100 0 400 800 1200 1600 2000 2400 2800 66
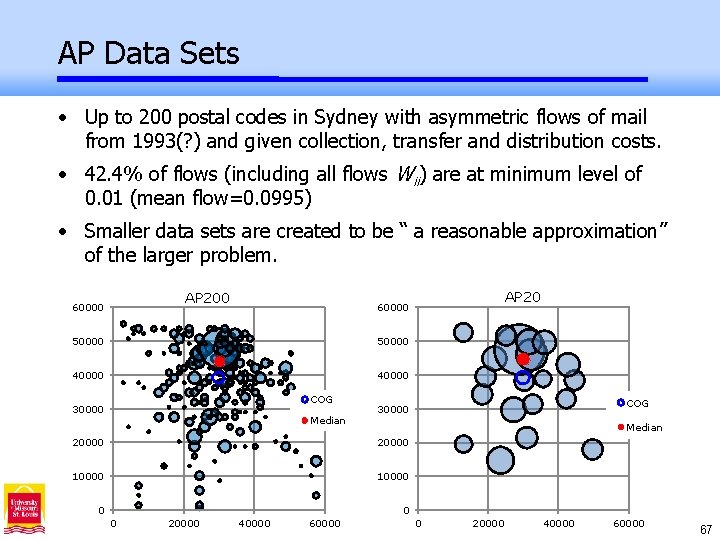
AP Data Sets • Up to 200 postal codes in Sydney with asymmetric flows of mail from 1993(? ) and given collection, transfer and distribution costs. • 42. 4% of flows (including all flows Wii) are at minimum level of 0. 01 (mean flow=0. 0995) • Smaller data sets are created to be “ a reasonable approximation” of the larger problem. AP 200 60000 AP 20 60000 50000 40000 COG 30000 Median 20000 10000 0 COG 30000 0 0 20000 40000 60000 67

Turkish network: TR 81 • 81 nodes for provinces in Turkey with asymmetric flows generated based on populations. • Often used with =0. 9 (from interhub travel time discount). • Smaller versions selected in various ways. TR 81 43 COG 42 1 -median 41 40 39 38 37 36 26 28 30 32 34 36 38 40 42 44 68
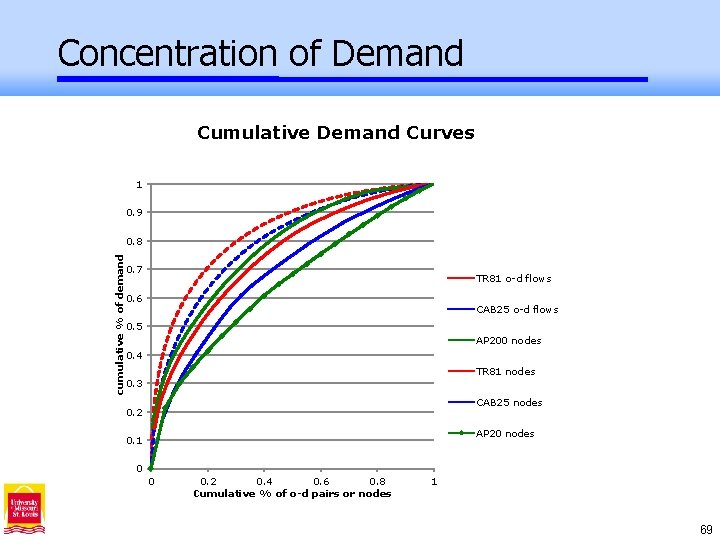
cumulative % of demand Concentration of Demand Cumulative % of o-d pairs or nodes 69
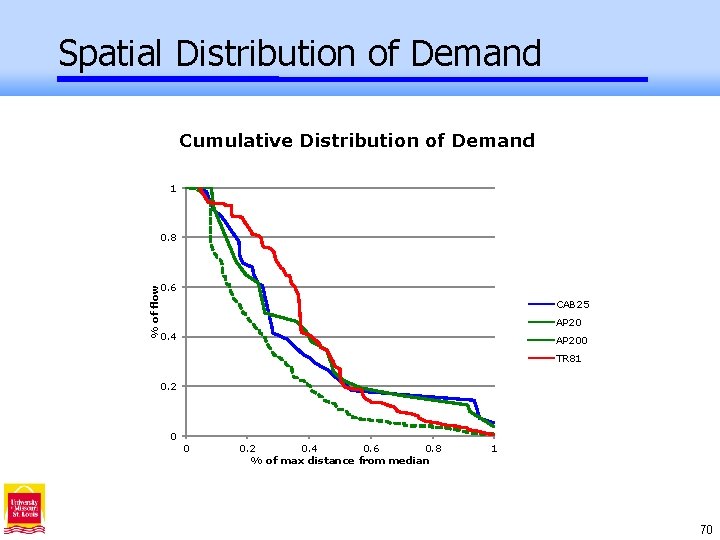
Spatial Distribution of Demand Cumulative Distribution of Demand 1 % of flow 0. 8 0. 6 CAB 25 AP 20 0. 4 AP 200 TR 81 0. 2 0 0 0. 2 0. 4 0. 6 0. 8 % of max distance from median 1 70

Distribution of Demand • Optimal hub locations and hub networks reflect the underlying distributions of flows (and aggregated flows). • All data sets have flows heavily concentrated in a few large nodes. • CAB is least centrally concentrated with large peripheral demand centers. • AP has concentrated demand is least evenly distributed over the region. - Subsets of AP may not be as similar to each other as “designed”. • TR 81 is most evenly distributed in space. 71
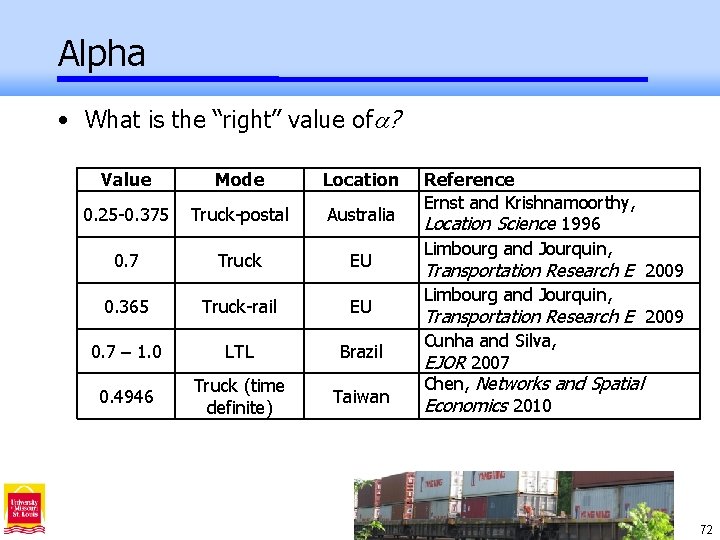
Alpha • What is the “right” value of ? Value Mode Location 0. 25 -0. 375 Truck-postal Australia 0. 7 Truck EU 0. 365 Truck-rail EU 0. 7 – 1. 0 LTL Brazil 0. 4946 Truck (time definite) Taiwan Reference Ernst and Krishnamoorthy, Location Science 1996 Limbourg and Jourquin, Transportation Research E 2009 Cunha and Silva, EJOR 2007 Chen, Networks and Spatial Economics 2010 72
New Directions for Hub Location Research • Better, more realistic models: - Incorporate cost, service and competition. - Model relevant costs (especially economies of scale) more accurately. - More complex networks with longer paths and direct routes. • Solve larger problems. (? ) • Link to service network design. • Link to telecom hub location. • Link to practice. 73

Questions? 74
- Slides: 74