How to win at poker using game theory

How to win at poker using game theory A review of the key papers in this field

The main papers on the issue v The first attempts – Émile Borel: ‘Applications aux Jeux des Hazard’ (1938) – John von Neumann and Oskar Morgenstern : ‘Theory of Games and Economic Behaviour’ (1944) v Extensions on this early model – Bellman and Blackwell (1949) – Nash and Shapley (1950) – Kuhn (1950) – Jason Swanson: Game theory and poker (2005) • Sundararaman (2009)

Jargon buster Fold: A Player gives up his/her hand. v Pot: All the money involved in a hand. v Check: A bet of ‘Zero’. v Call: Matching the bet of the previous player. v Ante: Money put into the pot before any cards have been dealt. v

Émile Borel: ‘Applications aux Jeux des Hazard’ (1938) v How the game is played – Two players – Two ‘cards’ • Each card is given a independent uniform value between 0 and 1 • Player 1’s card is X, Player 2’s Card is Y – No checking in this game – No raising or re-raising

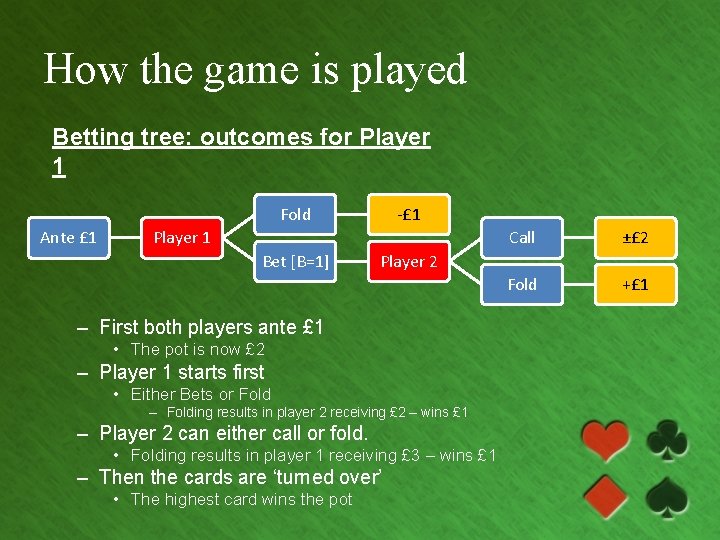
How the game is played Betting tree: outcomes for Player 1 Fold Ante £ 1 -£ 1 Player 1 Bet [B=1] ±£ 2 Fold +£ 1 Player 2 – First both players ante £ 1 • The pot is now £ 2 – Player 1 starts first • Either Bets or Fold – Folding results in player 2 receiving £ 2 – wins £ 1 – Player 2 can either call or fold. • Folding results in player 1 receiving £ 3 – wins £ 1 – Then the cards are ‘turned over’ • The highest card wins the pot Call

Émile Borel: ‘Applications aux Jeux des Hazard’ (1938) v Key assumptions – No checking – X≠Y (Cannot have same cards) – Money in the pot is an historic cost (sunk cost) and plays no part in decision making.

Émile Borel: ‘Applications aux Jeux des Hazard’ (1938) Key Conclusions – Unique admissible optimal strategies exist for both players • Where no strategy does any better against one strategy of the opponent without doing worse against another – it’s the best way to take advantage of mistakes an opponent may make. – The game favours Player 2 in the long run • The expected winnings of player 2 is 11% when B=1 – The optimum strategies exists • player 1 is to bet unless X<0. 11 where he should fold. • player 2 is to call unless Y<0. 33 where he should fold – Player 1 can aim to capitalise on his opponents mistakes by bluffing

John von Neumann and Oskar Morgenstern : ‘Theory of Games and Economic Behaviour’ (1944) v New key assumption: – Player 1 can now check v New conclusions – Player 1 should bluff with his worst hands – The optimum bet is size of the pot

One Card Poker 3 Cards in the Deck {Ace, Deuce, Trey} v 2 Players – One Card Each v Highest Card Wins v Players have to put an initial bet (‘ante’) before they receive their card v A round of betting occurs after the cards have been received v The ‘dealer’ always acts second v

One Card Poker v Assumptions – Never fold with a trey – Never call with the ace – Never check with the trey as the dealer – ‘Opener’ always checks with the deuce

One Card Poker v Conclusions – Dealer should call with the deuce 1/3 of the time – Dealer should bluff with the ace 1/3 of the time – If the dealer plays optimally the whole time, then expected profit will be 5. 56%

Thank You for Listening!