How To Solve Poisson Equation with Neumann Boundary

How To Solve Poisson Equation with Neumann Boundary Values Jin Chen CPPG

Background F equation in M 3 D (Auxiliary quantities related to perturbed toroidal flux)

Outlines • • • Characteristics of Neumann Boundary Values Numerical singularity of such Boundary Values Null Space method for such singularity CG and GMRES for non-singular linear equation Null Space based CG and GMRES for singular linear equation • Application to eigenvalue problem • Application to M 3 D

Characteristics of Neumann Boundary Values • Solvability not every system of equation has a solution. • Unique if u is a solution, so is u + c.

Eigenvalues of the Poisson Equation with Neumann BV

Is there anything we can do? Let’s assume A is non-singular FIRST. • Direct solver • Iterative solver Krylov Subspace Methods.

Iterative solver

Krylov Subspace Methods… • Conjugate Gradient (CG) symmetric positive definite matrix • Generalized Minimal Residual (GMRES) non-symmetric indefinite matrix

CG

GMRES

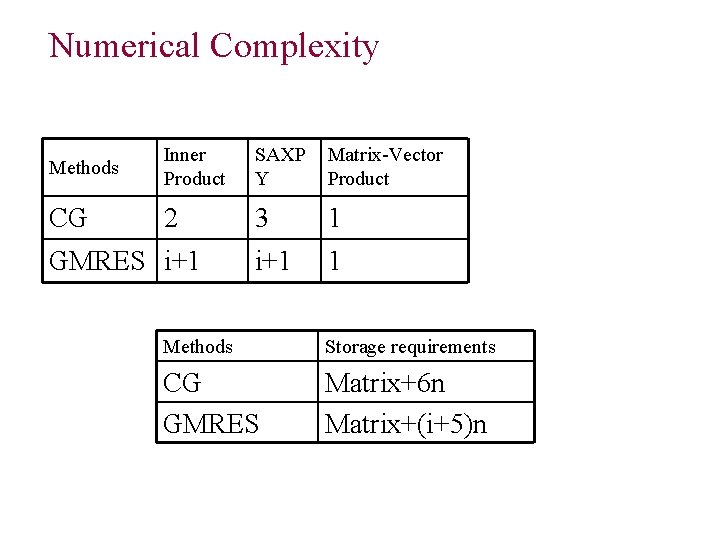
Numerical Complexity Methods Inner Product SAXP Y Matrix-Vector Product CG 2 3 1 i+1 1 GMRES i+1 Methods Storage requirements CG GMRES Matrix+6 n Matrix+(i+5)n

If A is singular … 1. Solvability 2. Unique Mean zero Least square solution

Definition of Null Space

Null Space

CG for singular systems

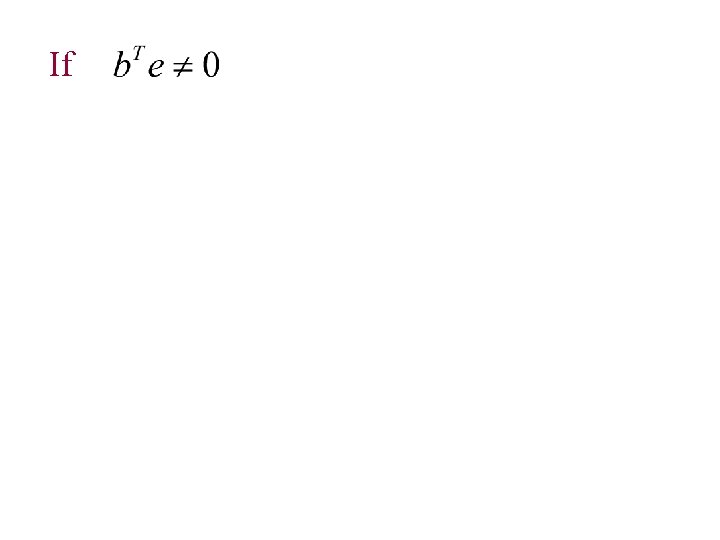
If

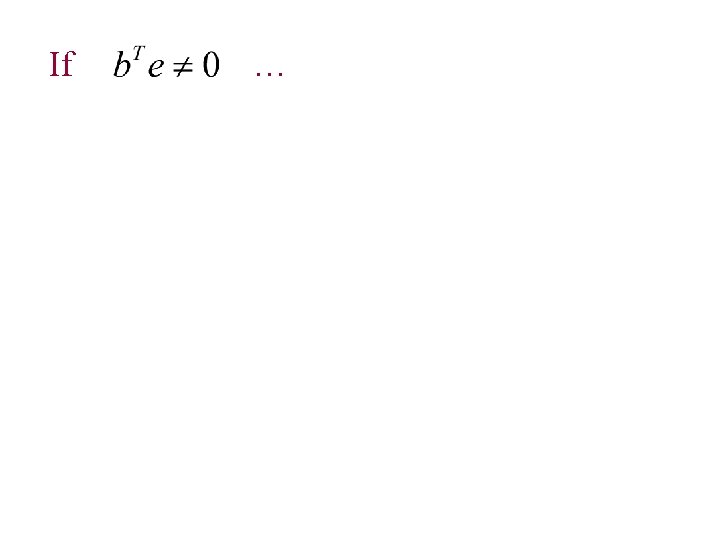
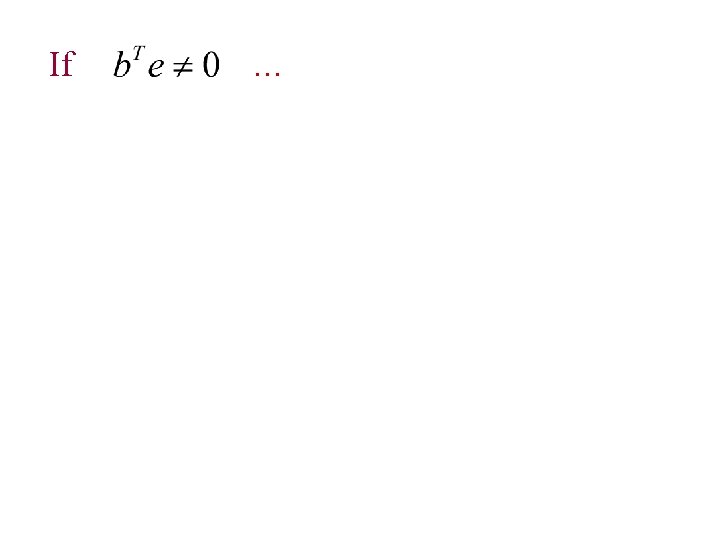
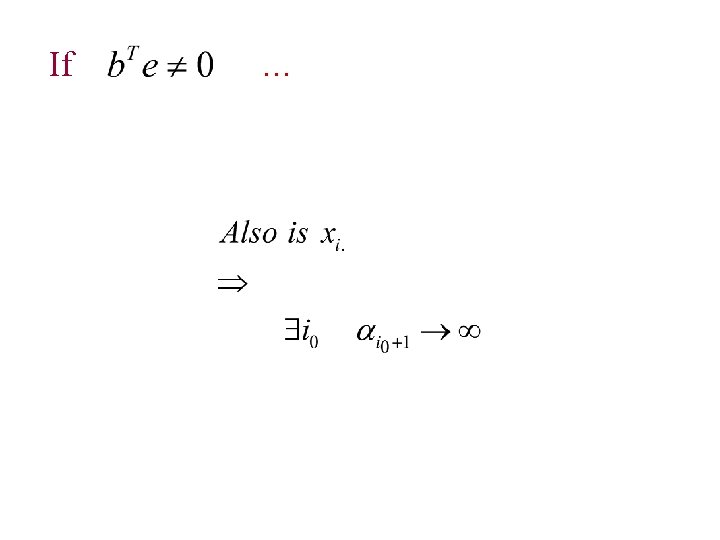
If … Re-orthogonlization To assure there exists a solution.

GMRES for singular systems

GMRES for singular systems …

Numerical Experiment

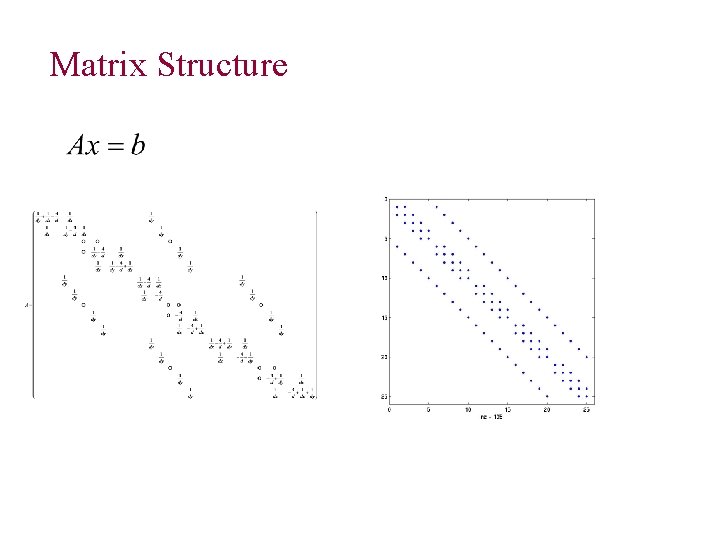
Matrix Structure

Singular and Solvability Check

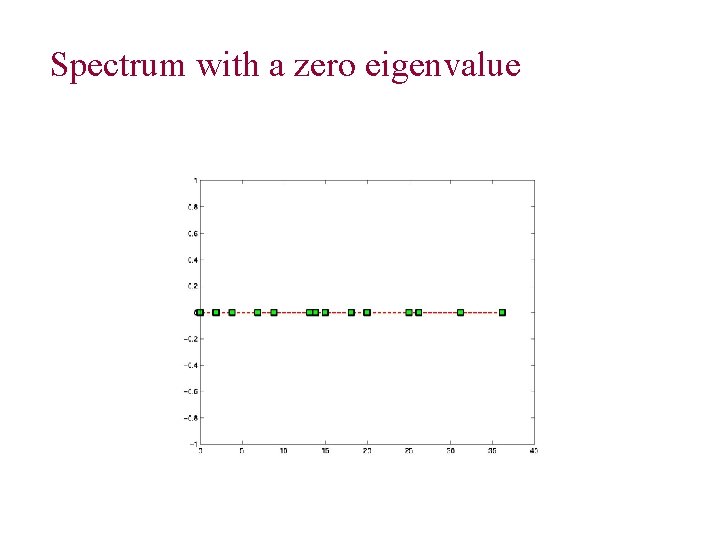
Spectrum with a zero eigenvalue

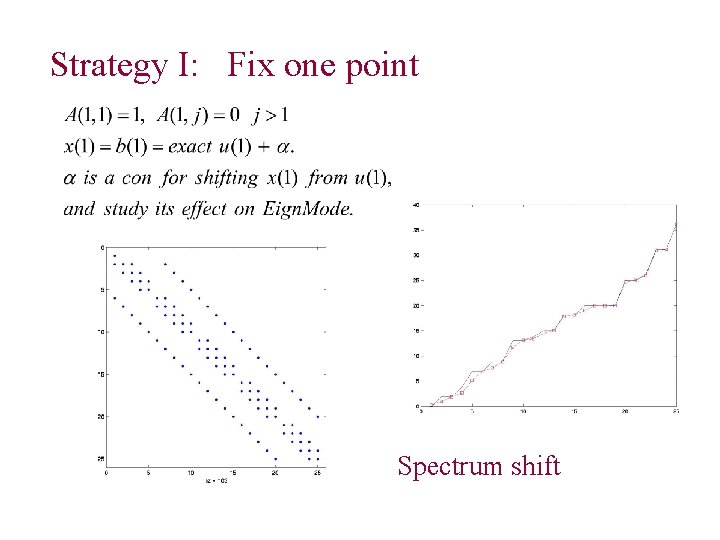
Strategy I: Fix one point Spectrum shift

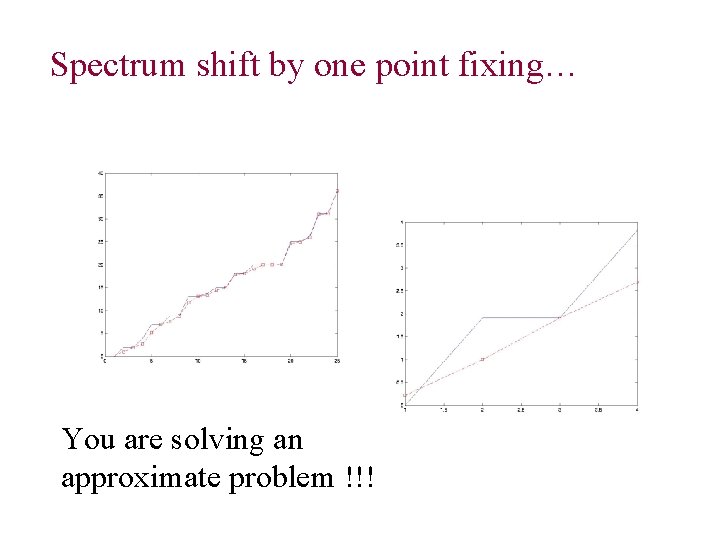
Spectrum shift by one point fixing… You are solving an approximate problem !!!

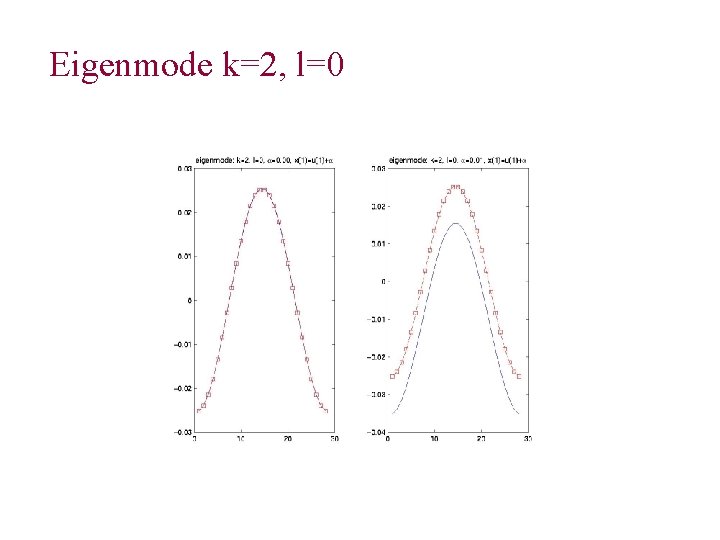
Eigenmode k=2, l=0

Strategy II: null space

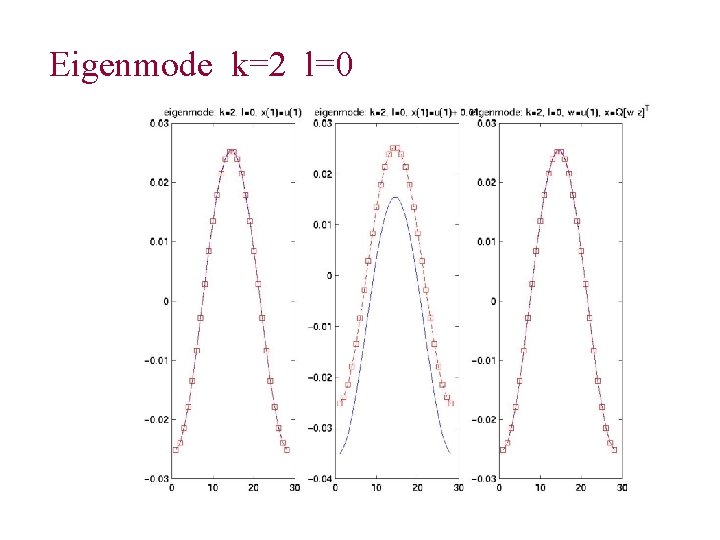
Eigenmode k=2 l=0

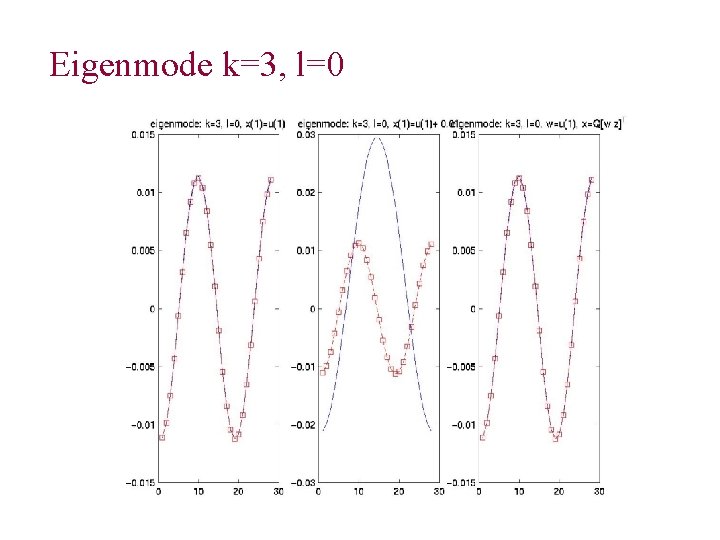
Eigenmode k=3, l=0

Application in M 3 D • • F equation, Singular check: Ae=0, Solvability check: (b, e)=0, Re-orthogonalization: b=b-(b, e)/(e, e), Uniqueness check: (x, e)=0, CG with nullspace, GMRES with nullspace,

If you want to try it…