How to prove that a problem is NPC

How to prove that a problem is NPC 1

Cook showed the first NPC problem: SAT n Cook received Turing Award in 1982. n 2

Karp R. Karp showed several NPC problems, such as 3 -STA, node (vertex) cover, and Hamiltonian cycle, etc. n Karp received Turing Award in 1985 n 3

NP-Completeness Proof: Reduction All NP problems SAT Clique Vertex Cover 3 -SAT Chromatic Number Dominating Set 4

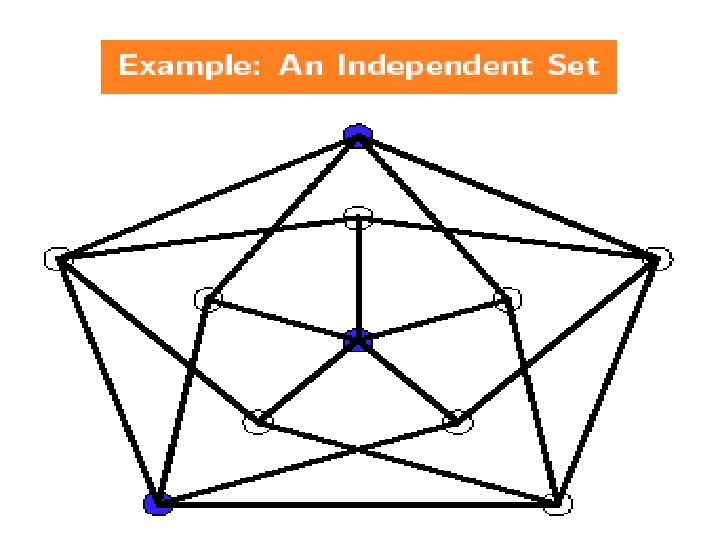
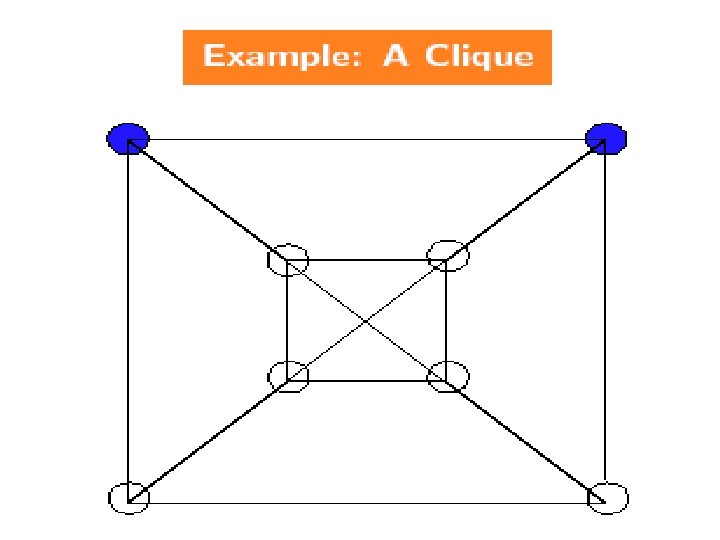
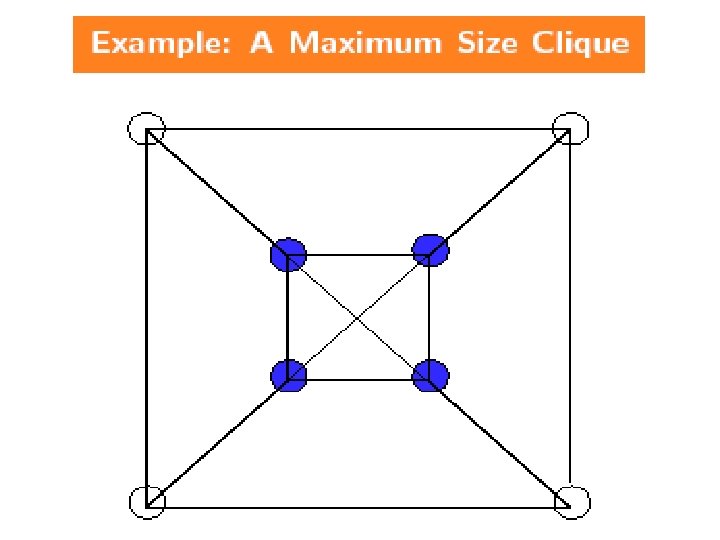
NPC Problems n CLIQUE(k): Does G=(V, E) contain a clique of size k? Definition: q A clique in a graph is a set of vertices such that any pair of vertices are joined by en edge. 13

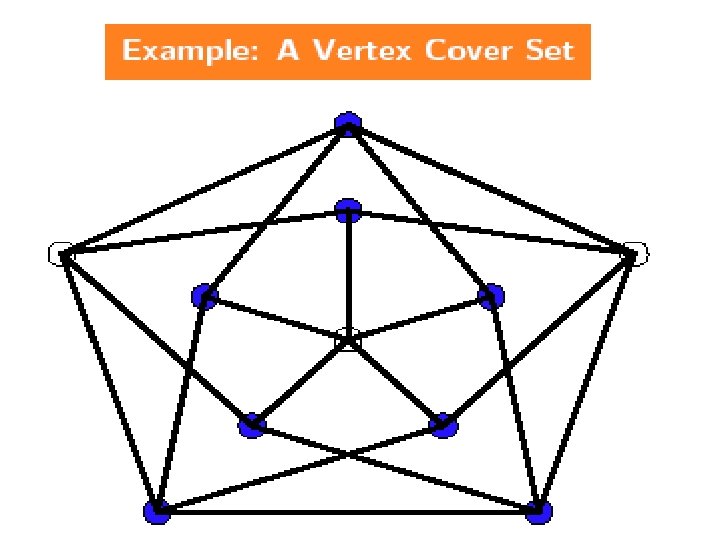
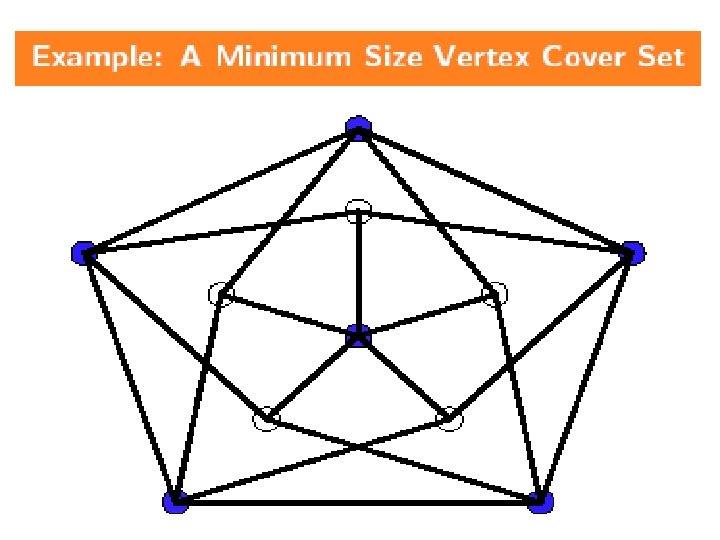
NPC Problems n Vertex Cover(k): Given a graph G=(V, E) and an integer k, does G have a vertex cover with k vertices? Definition: n A vertex cover of G=(V, E) is V’ V such that every edge in E is incident to some v V’. 14

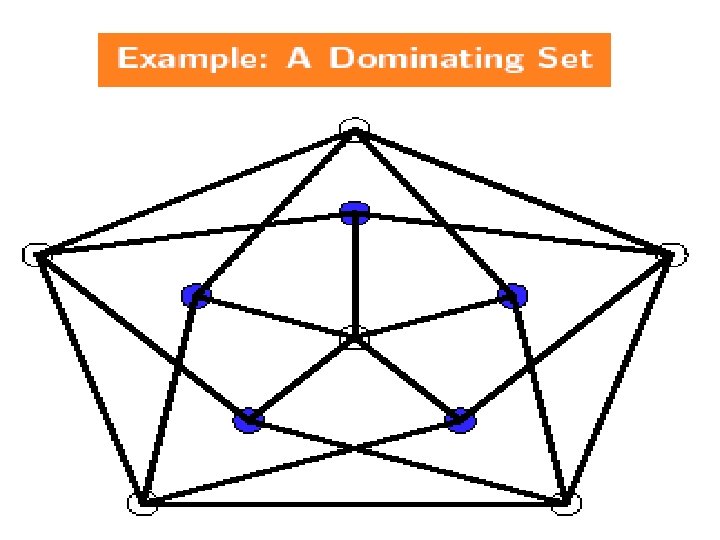
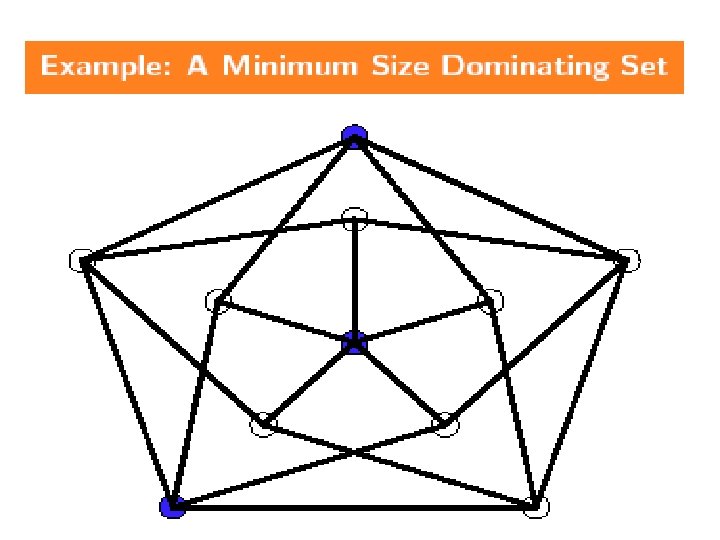
NPC Problems Dominating Set(k): Given an graph G=(V, E) and an integer k, does G have a dominating set of size k ? Definition: q A dominating set D of G=(V, E) is D V such that every v V is either in D or adjacent to at least one vertex of D. n 15

NPC Problems • • SAT: Give a Boolean expression (formula) in DNF (conjunctive normal form), determine if it is satisfiable. 3 SAT: Give a Boolean expression in DNF such that each clause has exactly 3 variables (literals), determine if it is satisfiable. 16

NPC Problems Chromatic Coloring(k): Given a graph G=(V, E) and an integer k, does G have a coloring for k Definition • n A coloring of a graph G=(V, E) is a function f : V { 1, 2, 3, …, k } if (u, v) E, then f(u) f(v). 17

3 -Satisfiability Problem (3 SAT) n n n Def: Each clause contains exactly three literals. (I) 3 -SAT is an NP problem (obviously) (II) SAT 3 -SAT Proof: (1) One literal L 1 in a clause in SAT: In 3 -SAT: L 1 v y 2 L 1 v -y 1 v y 2 L 1 v y 1 v -y 2 L 1 v -y 2 18

(2) Two literals L 1, L 2 in a clause in SAT: In 3 -SAT: L 1 v L 2 v y 1 L 1 v L 2 v -y 1 (3) Three literals in a clause: remain unchanged. (4) More than 3 literals L 1, L 2, …, Lk in a clause: in 3 -SAT: L 1 v L 2 v y 1 L 3 v -y 1 v y 2 Lk-2 v -yk-4 v yk-3 Lk-1 v Lk v -yk-3 19

Example of Transforming a 3 -SAT Instance to an SAT Instance n An instance S in SAT: x 1 v x 2 -x 3 x 1 v -x 2 v x 3 v -x 4 v x 5 SAT S n transform The instance x 1 v -x 3 v x 1 v x 3 v -x 4 v S in 3 -SAT: x 2 v y 1 x 2 v -y 1 y 2 v y 3 -y 2 v y 3 y 2 v -y 3 -x 2 v y 4 -y 4 v y 5 x 5 v -y 5 3 -SAT S 20

Chromatic Number Decision Problem (CN) n n Def: A coloring of a graph G = (V, E) is a function f: V { 1, 2, 3, …, k } such that if (u, v) E, then f(u) f(v). The CN problem is to determine if G has a coloring for k. E. g. 3 -colorable f(a)=1, f(b)=2, f(c)=1 f(d)=2, f(e)=3 <Theorem> Satisfiability with at most 3 literals per clause (SATY) CN. 21

Set Cover Decision Problem n Def: F = { S 1, S 2, …, Sk } Si = { u 1, u 2, …, un } T is a set cover of F if T F and Si = Si The set cover decision problem is to determine if F has a cover T containing no more than c sets. n Example: c=3. F = {(a 1, a 3), (a 2, a 4), (a 2, a 3), (a 4), (a 1, a 3 , a 4)} s 1 s 2 s 3 s 4 s 5 T = { s 1, s 3, s 4 } set cover T = { s 1, s 2 } another set cover 22

Exact Cover Problem Def: To determine if F has an exact cover T, which is a cover of F and the sets in T are pairwise disjoint. <Theorem> CN exact cover 23

Sum of Subsets Problem n n Def: A set of positive numbers A = { a 1, a 2, …, an } a constant C Determine if A A ai = C e. g. A = { 7, 5, 19, 1, 12, 8, 14 } n n C = 21, A = { 7, 14 } C = 11, no solution <Theorem> Exact cover sum of subsets. 24

Exact Cover Sum of Subsets n Proof: Instance of exact cover: F = { S 1, S 2, …, Sn } Instance of sum of subsets: A = { a 1, a 2, …, an } where 25

Partition Problem n Def: Given a set of positive numbers A = { a 1, a 2, …, an }, determine if a partition P, ai = ai i p n i p e. g. A = {3, 6, 1, 9, 4, 11} partition: {3, 1, 9, 4} and {6, 11} <Theorem> sum of subsets partition 26

Bin Packing Problem n n Def: n items, each of size ci , ci > 0, a positive number k and bin capacity C, determine if we can assign the items into k bins such that the sum of ci’s assigned to each bin does not exceed C. <Theorem> partition bin packing. 27

Q&A 28