How to measure the performance of an algorithm

How to measure the performance of an algorithm

Measuring the performance • The properties of an algorithm which relate to the amount of computational resources used by the algorithm. • how fast or slow particular algorithm performs • how much space particular algorithm performs • depends on the input (sorted vs. unsorted input array) • Frequently measured based on the worst case • Also on average case (difficult) • Sometimes on best case • Asymptotic notation - "Big Oh"

Cuanto demora la búsqueda del máximo ? • There are 2 instruction that are performed only once • Lets say they take A • There are 2 instructions and one comparission that are perforrmed n times • Lets say it takes Bn • In total A +Bn : for a big n the term A can be neglected • We say the algoritm is order n or O(n) static int mindex(int[] a) { int m =0, k = 1; while(k <= a. length){ if (a[k] > a[m] ) m = k; k++ return m; }

Cuanto demora select sorting ?

Intuitivamente: se elige el termino mayor • Typically in algorithms we find • K log n < K n 2 < K n 3. . . < K 2 n • We talk then that the algorithm ir order f(n) or O(f(n)) • Like O(logn) O(n log n ) • Unfortunately this is too easy: there is a formal definition

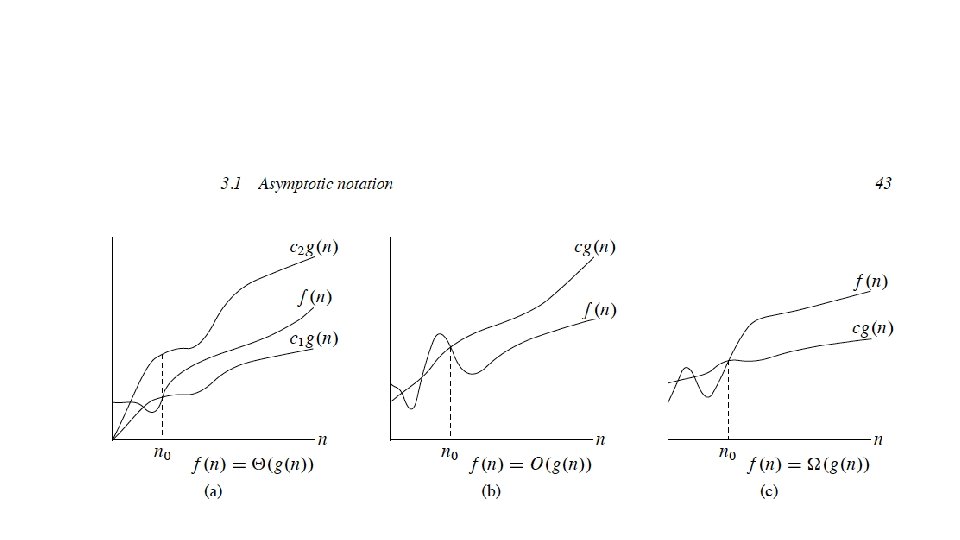
Notación O • Se dice que una función f (n) es O(g(n)) si existe una constante c > 0 y un n 0 >= 0 tal que para todo n >= n 0 se tiene que f (n) <= cg(n). (cota superior de un algoritmo) • Se dice que una función f (n) es Ω(g(n)) si existe una constante c > 0 y un n 0 >= 0 tal que para todo n >= n 0 se tiene que f (n) >= cg(n). (cota inferior) • Se dice que una función f (n) es Θ (g(n)) si f (n) = O(g(n)) y f (n) = Ω(g(n)).

Subsecuencia de suma máxima • Dados enteros A 1, …, An (posiblemente negativos), encontrar el maximo valor de • Si todos los números son negativos, la subsecuencia de suma máxima es 0 9

Subsecuencia de suma máxima • Ejemplo: • Secuencia: -2, 11, -4, 13, -5, -2 • Respuesta: 20 • Veremos cuatro soluciones distintas para este problema • Primera solución (fuerza bruta): • Calcular la suma de todas las subsecuencias • Quedarse con la suma mayor 10

Subsecuencia de suma máxima • Solución 1: Fuerza bruta int max. Sum = 0; for( i=0; i<a. length; i++) { for( j=i; j<a. length; j++) { int this. Sum = 0; for (k=i; k<=j; k++) this. Sum += a[k]; if (this. Sum > max. Sum) max. Sum = this. Sum; } } 11

Subsecuencia de suma máxima • Tiempo: O(n 3) 12

Subsecuencia de suma máxima • Segunda solución (mejora fuerza bruta) • Notar que • Por lo tanto, el tercer ciclo for se puede eliminar 13

Subsecuencia de suma máxima • Solución 2: Mejora a fuerza bruta int max. Sum = 0; for( i=0; i<a. length; i++) { int this. Sum = 0; for (j=i; j<=a. length; j++) { this. Sum += a[j]; if (this. Sum > max. Sum) max. Sum = this. Sum; } } 14

Subsecuencia de suma máxima • Tiempo: O(n 2) • Solución 3: Usando “dividir para reinar” • • Idea: dividir el problema en dos subproblemas del mismo tamaño Resolver recursivamente Mezclar las soluciones Obtener solución final 15

Subsecuencia de suma máxima • Solución 4: Algoritmo eficiente • Inducción (reforzada) • Se conoce la mejor subsecuencia entre 1 y j • Se conoce la mejor subsecuencia que termina en j • Algoritmo • • Se almacenan ambos valores (inicialmente 0) Se incrementa j en 1 Se actualiza mejor subsecuencia si es necesario Si subsecuencia que termina en j es < 0 se puede descartar, volver su valor a 0 16

Subsecuencia de suma máxima • Seudocódigo int max. Sum = 0, this. Sum = 0; for( j=0; j<a. length; j++) { this. Sum += a[j]; if (this. Sum > max. Sum) max. Sum = this. Sum; else if (this. Sum < 0) this. Sum = 0; } 17

Subsecuencia de suma máxima • Tiempo de la solución eficiente: O(n) 18