How to implement Bayesian statistics to Make Lifecycle

How to implement Bayesian statistics to Make Lifecycle Strategy a Reality that Serves Quality Steven Novick, Katherine Giacoletti, Tara Scherder, and Bruno Boulanger Steven. Novick@arlenda. com

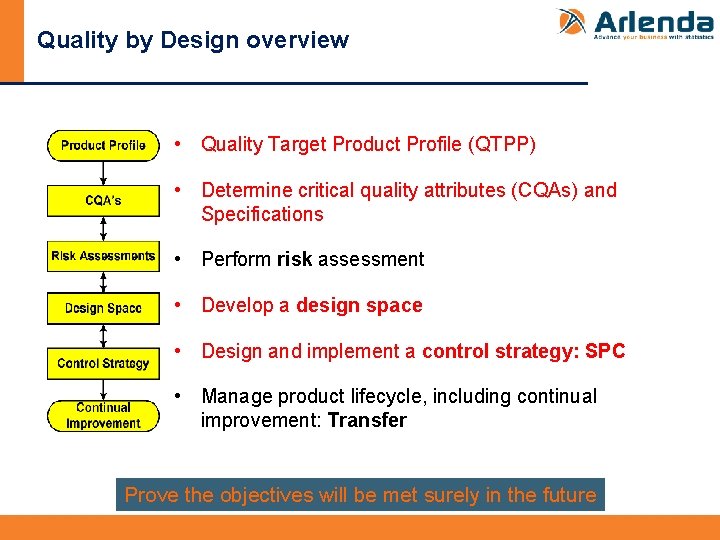
Quality by Design overview • Quality Target Product Profile (QTPP) • Determine critical quality attributes (CQAs) and Specifications • Perform risk assessment • Develop a design space • Design and implement a control strategy: SPC • Manage product lifecycle, including continual improvement: Transfer Prove the objectives will be met surely in the future

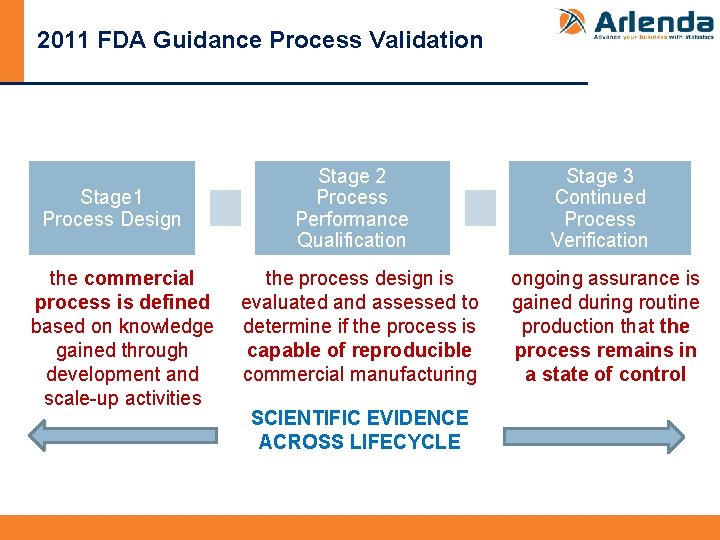
2011 FDA Guidance Process Validation Stage 1 Process Design the commercial process is defined based on knowledge gained through development and scale-up activities Stage 2 Process Performance Qualification the process design is evaluated and assessed to determine if the process is capable of reproducible commercial manufacturing SCIENTIFIC EVIDENCE ACROSS LIFECYCLE Stage 3 Continued Process Verification ongoing assurance is gained during routine production that the process remains in a state of control

Excerpt from Guidance • “…high degree of assurance on the performance of the manufacturing process that will consistently produce…. ” • “ …. collection and evaluation of data … which establishes scientific evidence that a process is capable of consistently delivering quality product…. ” • “ … the assurance should be obtained from objective information and data from laboratory, pilot batches…. ”

Excerpt from Guidance • “During the process qualification (PQ) stage of process validation, the process design is evaluated to determine if it is capable of reproducible commercial manufacture…” What is “capable”? Capability is defined as the ability of a process to meet specification

Bayesian principle “PRIOR DISTRIBUTION” from previous studies, expert opinion, literature, … Available Data + Observed Data “LIKELIHOOD” data coming from the experiment = Total Data “POSTERIOR DISTRIBUTION” for parameters combination of information collected before the experiment and what comes from the experimental data

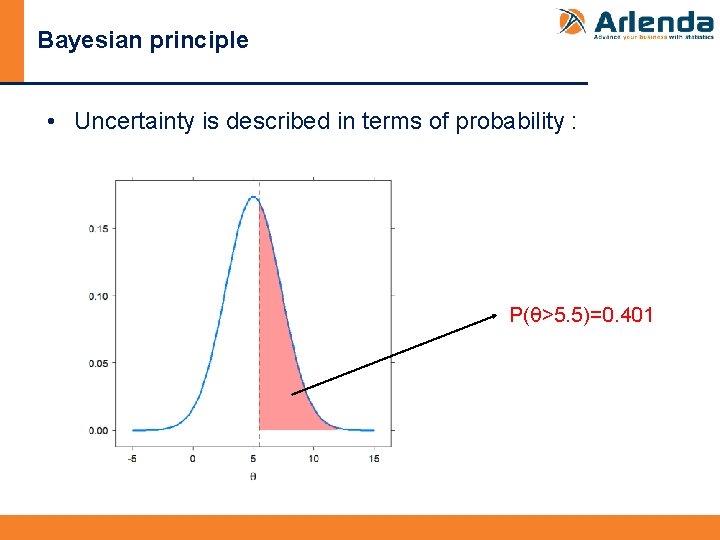
Bayesian principle • Uncertainty is described in terms of probability : P(θ>5. 5)=0. 401

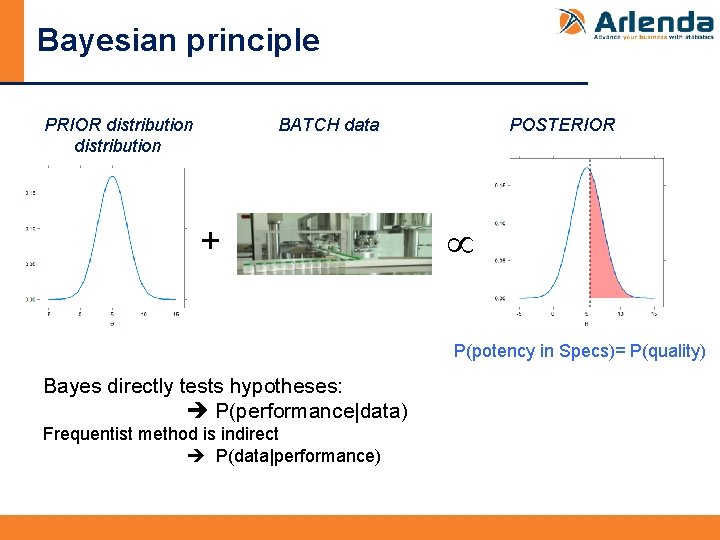
Bayesian principle PRIOR distribution BATCH data + POSTERIOR P(potency in Specs)= P(quality) Bayes directly tests hypotheses: P(performance|data) Frequentist method is indirect P(data|performance)

Bayesian principle • PPQ batches are produced to collect evidence of the quality of the process -Frequentist analysis: • Point estimate and confidence intervals as summaries of process (mean and sd) What do PPQ batches tell us about the process? -Bayesian analysis: • Before the PPQ: a priori opinion on the process How should those PPQ batches change our opinion about the process? How should those PPQ batches provide assurance about future batches? • Motivations for adopting Bayesian approach: Natural and coherent way of thinking about learning and risk

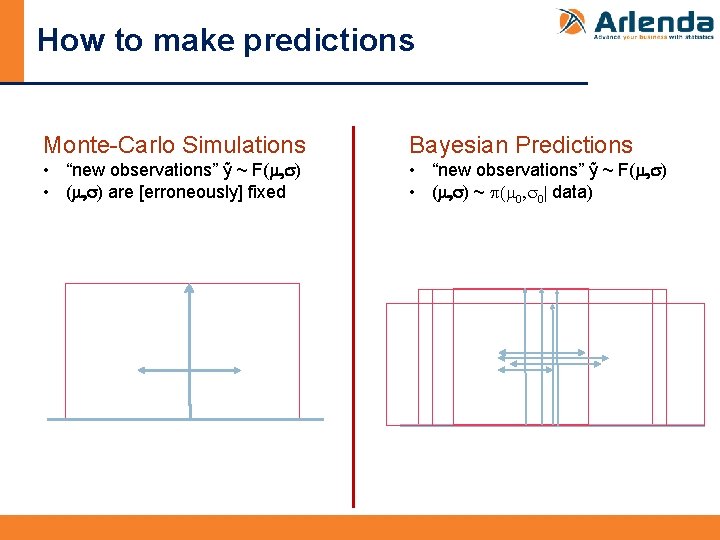
How to make predictions Monte-Carlo Simulations Bayesian Predictions • “new observations” ỹ ~ F(m, s) • (m, s) are [erroneously] fixed • “new observations” ỹ ~ F(m, s) • (m, s) ~ p(m 0, s 0| data)

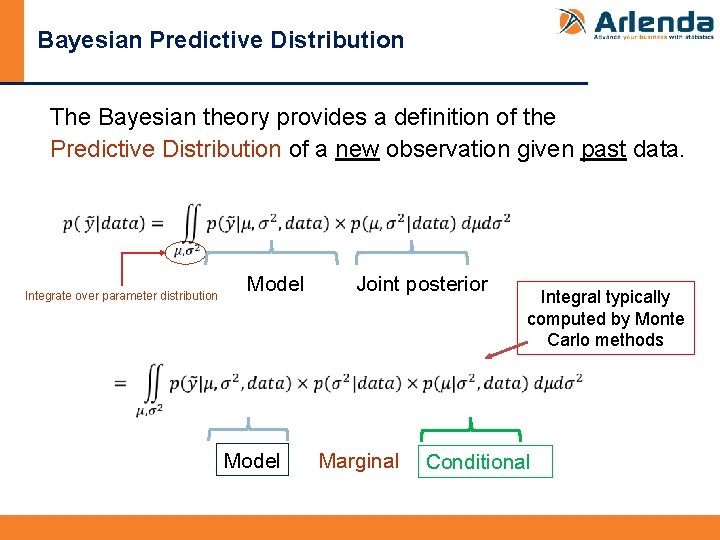
Bayesian Predictive Distribution The Bayesian theory provides a definition of the Predictive Distribution of a new observation given past data. Integrate over parameter distribution Model Joint posterior Marginal Integral typically computed by Monte Carlo methods Conditional

Comparison Frequentist vs Bayesian • When NON-informative priors are envisioned -Posteriors and HPD (~quantiles) are the same as the Frequentist results Are non-informative priors defensible in Stage 2?

There are defensible priors • Once decision is made to go through PPQ, there is belief it will work. • Translate those scientific evidence and data based into priors • Priors contain the whole uncertainty about this belief. This is the prior elicitation process. • Classical statistics ignores prior available information.

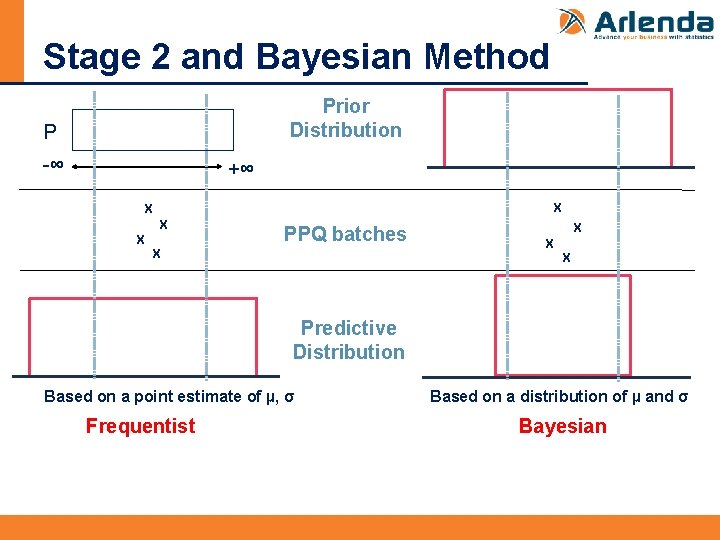
Stage 2 and Bayesian Method Prior Distribution P -∞ +∞ X X PPQ batches X X Predictive Distribution Based on a point estimate of µ, σ Frequentist Based on a distribution of µ and σ Bayesian

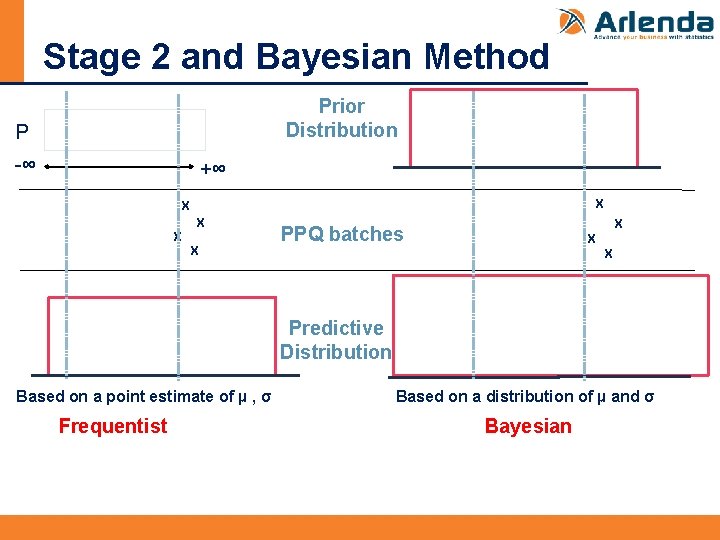
Stage 2 and Bayesian Method Prior Distribution P -∞ +∞ X X X PPQ batches X X Predictive Distribution Based on a point estimate of µ , σ Frequentist Based on a distribution of µ and σ Bayesian

Probability being in specifications vs Tolerance intervals • Use the Predictive distribution to compute the prob. to be within specs Predictive posterior X X Bayesian method directly calculates risk [-----------] Tolerance Interval Frequentist tolerance interval indirectly assesses risk

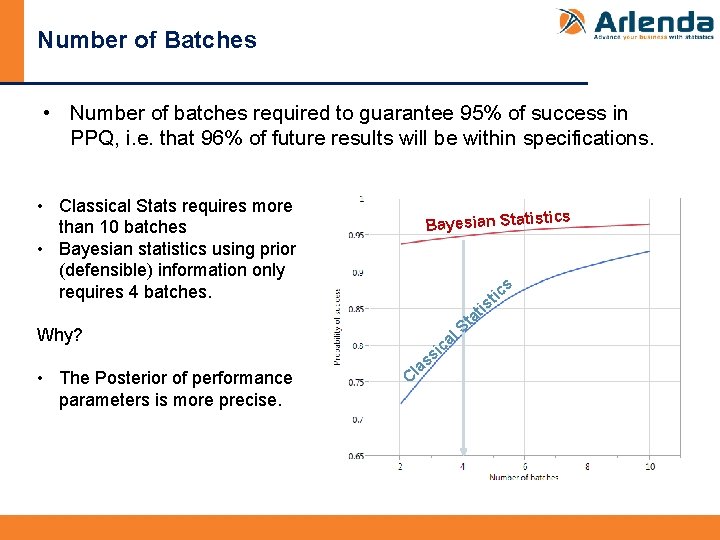
Number of Batches • Number of batches required to guarantee 95% of success in PPQ, i. e. that 96% of future results will be within specifications. • Classical Stats requires more than 10 batches • Bayesian statistics using prior (defensible) information only requires 4 batches. cs Bayesian Statisti s Why? • The Posterior of performance parameters is more precise. Cl al c si s a S tic s ti ta

Other Benefits of Bayesian Approach • Capability is defined as the ability of a process to meet specification, that is, the probability of meeting specification Bayesian provides a true prediction of future performance • Handles complicated hierarchy/ sampling plan -Between batch, sample within batch, within sample variation can be incorporated -Unbalanced sampling • Joint prediction of multiple CQAs is possible • Uncertainty of parameters included, thus improving prediction and reducing risk • Not affected by non-centering within specification range • Systems approach to unit operations (simultaneous prediction)

Stage 1 - Design Space and Predictions • In Stage 1 the objective is to identify the Design Space • Do. E are performed to understand the relationships between the CPP and the CQA • The known or assumed control/uncertainty on CPPs can be integrated into Predictions • The set of CPP (X) that guarantee results are in specifications is called the Design Space.

An example: Spray-drying process • Spray-drying is intended to create a powder with small and controlled particle size for pulmonary delivery of a drug substance • Several Critical Process Parameters (CPP) have an influence on several Critical Quality Attributes (CQA) - Inlet temperature - Spray flow-rate - Feed rate (other process parameters are kept constant) • Specifications on CQA defined as minimal satisfactory quality - Yield > 80% - Moisture < 1% - Inhalable fraction > 60% -…

Focusing only on the mean (average) can put us at risk! Average depth of river is 3 feet. The Flaw of Averages: Why We Underestimate Risk in the Face of Uncertainty by Dr. Sam Savage From John Peterson, 2012

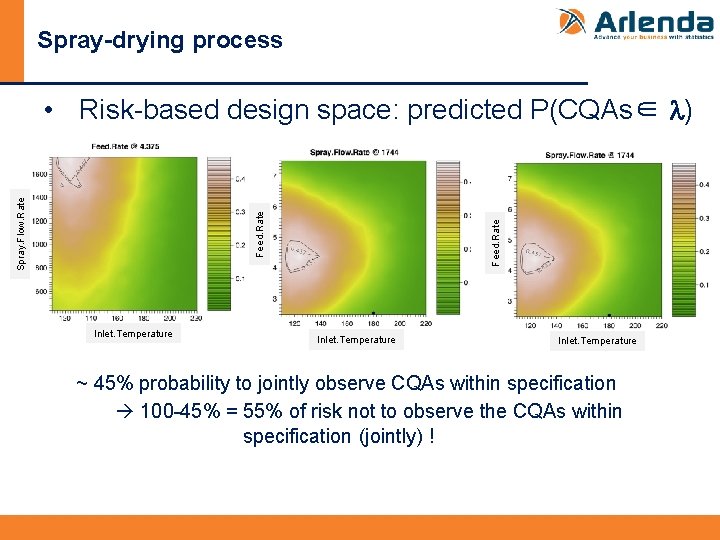
Spray-drying process Feed. Rate Spray. Flow. Rate • Risk-based design space: predicted P(CQAs∈ l) In the Design Space, there is 45% of chance to observe each CQA within specification, jointly Inlet. Temperature ~ 45% probability to jointly observe CQAs within specification 100 -45% = 55% of risk not to observe the CQAs within specification (jointly) !

Spray-drying process • Validation -Experiments have been repeated 3 times independently at optimal condition, i. e. Inlet Temperature: 123. 75°C Spray Flow Rate: 1744 L/h Feed Rate: 4. 69 ml/min Jointly, 2 out of the 3 runs within specification

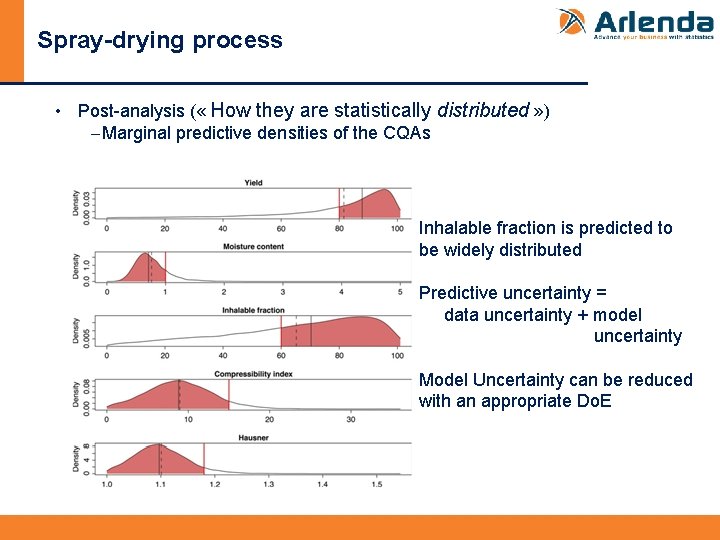
Spray-drying process • Post-analysis ( « How they are statistically distributed » ) -Marginal predictive densities of the CQAs Inhalable fraction is predicted to be widely distributed Predictive uncertainty = data uncertainty + model uncertainty Model Uncertainty can be reduced with an appropriate Do. E

Stage 3

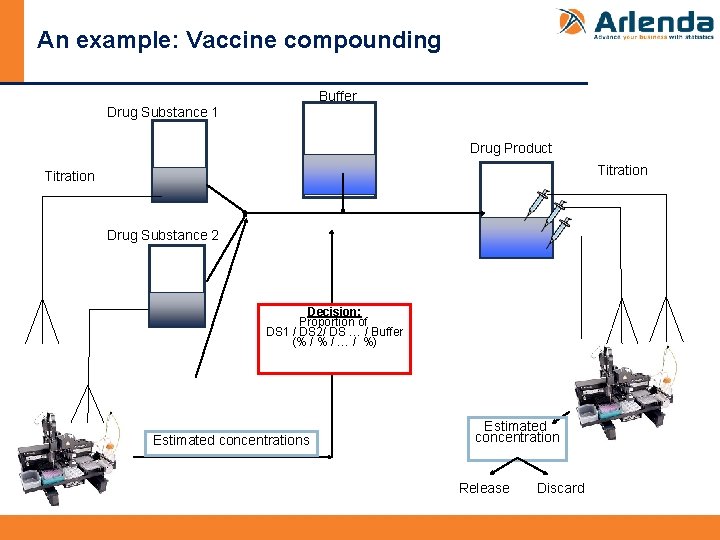
An example: Vaccine compounding Buffer Drug Substance 1 Drug Product Titration Drug Substance 2 Decision: Proportion of DS 1 / DS 2/ DS … / Buffer (% / … / %) Estimated concentrations Estimated concentration Release Discard

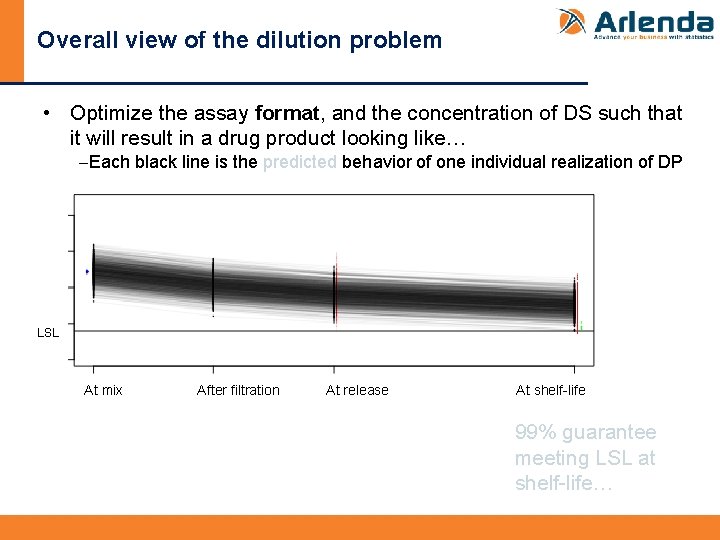
Overall view of the dilution problem • Optimize the assay format, and the concentration of DS such that it will result in a drug product looking like… -Each black line is the predicted behavior of one individual realization of DP LSL At mix After filtration At release At shelf-life 99% guarantee meeting LSL at shelf-life…

Control strategy • Control strategy is defined based on the (simulated) outcome of the process profile at strategic intermediate testing (red) • The prediction interval (b-expectation tolerance interval) can be used as control limits.

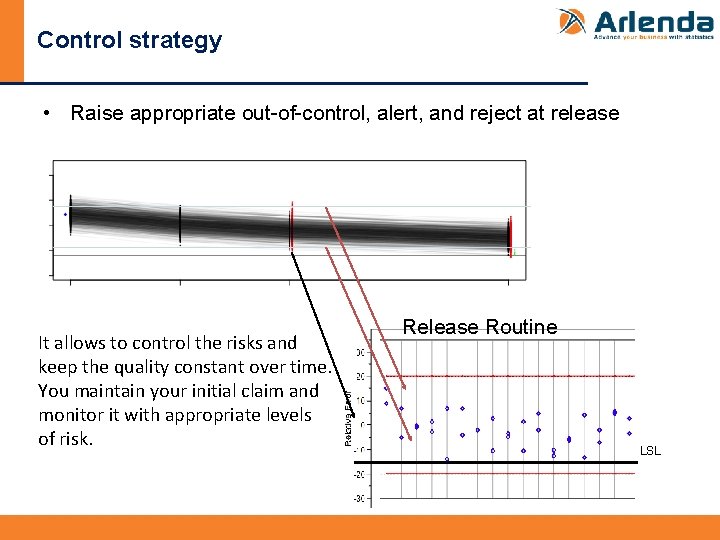
Control strategy • Raise appropriate out-of-control, alert, and reject at release It allows to control the risks and keep the quality constant over time. You maintain your initial claim and monitor it with appropriate levels of risk. Release Routine LSL

Conclusion • Bayesian statistics provide a natural answer to all Stages of process or method development • Bayesian statistics provide predictive distribution to permit prediction-based decision • Prediction are key to Design Space • Prediction are key to PPQ • Bayesian statistics make multivariate modeling easy and allows to compute joint probability of success • Bayesian statistics are easy to compute today with languages such as SAS, BUGS, JAGS, or STAN.

Thank you!