How to draw a hyperbolic paraboloid John Ganci

How to draw a hyperbolic paraboloid John Ganci Adjunct Math Faculty Richland CC, Dallas TX jganci@dcccd. edu Al Lehnen Math Instructor Madison Area Technical College, Madison WI alehnen@matcmadison. edu

The steps • • • Identify the axis Identify the parabolas Draw two hyperbolas Connect the hyperbolas

Identify the axis • Write equation in the form – u, v, and w are x, y, and z • u = x, v = y, w = z • u = y, v = x, w = z • u = z, v = x, w = y u = x, v = z, w = y u = y, v = z, w = x u = z, v = y, w = x • The one of degree 1, u, is the axis • If the equation is, • Then u = x, v = y, w = z, a = 1, b = 1 axis is the x-axis

Identify the parabolas • Two parabolas are used for the sketch • The remaining two variables in the equation, v and w, are used for the parabolas • the “upper parabola” • the “lower parabola” • For • the “upper parabola” is • the “lower parabola” is

Draw the parabolas • The upper parabola is in the uv-plane • The lower parabola is in the uw-plane • For – The upper parabola is in the xy-plane – The lower parabola is in the xz-plane • Determine “reasonable” limits for the domain values for the two parabolas – Upper: x = y^2; limit y to [-2, 2] or [-1, 1] – Lower: x = -z^2; limit z to [-2, 2] or [-1, 1]
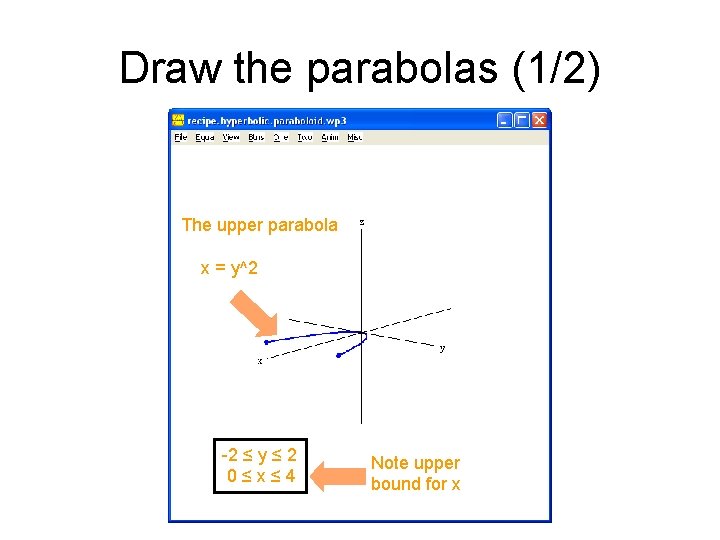
Draw the parabolas (1/2) The upper parabola x = y^2 -2 ≤ y ≤ 2 0≤x≤ 4 Note upper bound for x
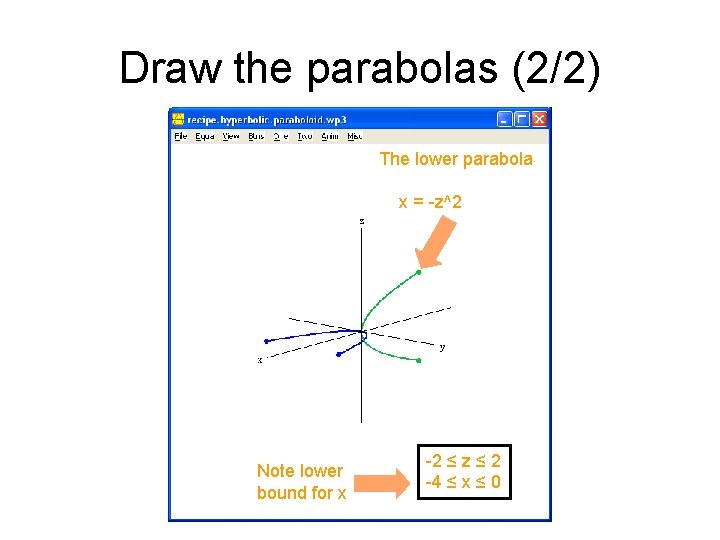
Draw the parabolas (2/2) The lower parabola x = -z^2 Note lower bound for x -2 ≤ z ≤ 2 -4 ≤ x ≤ 0

Draw the hyperbolas • One hyperbola for each of the parabolas • Drawn in planes perpendicular to the axis • Upper hyperbola drawn with upper parabola – The plane is the upper bound for the u variable • For • this is the plane x = 4 – Vertices are on the upper parabola • Lower hyperbola drawn with lower parabola – The plane is the lower bound for the u variable • For • this is the plane x = – 4 – Vertices are on the lower parabola
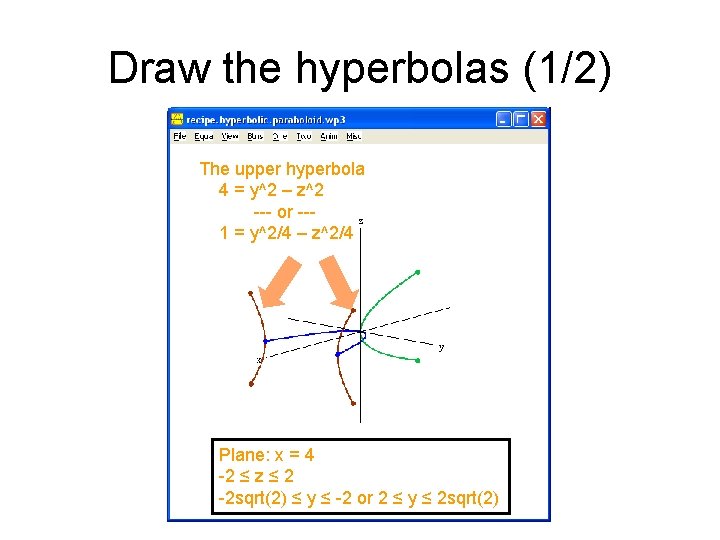
Draw the hyperbolas (1/2) The upper hyperbola 4 = y^2 – z^2 --- or --1 = y^2/4 – z^2/4 Plane: x = 4 -2 ≤ z ≤ 2 -2 sqrt(2) ≤ y ≤ -2 or 2 ≤ y ≤ 2 sqrt(2)
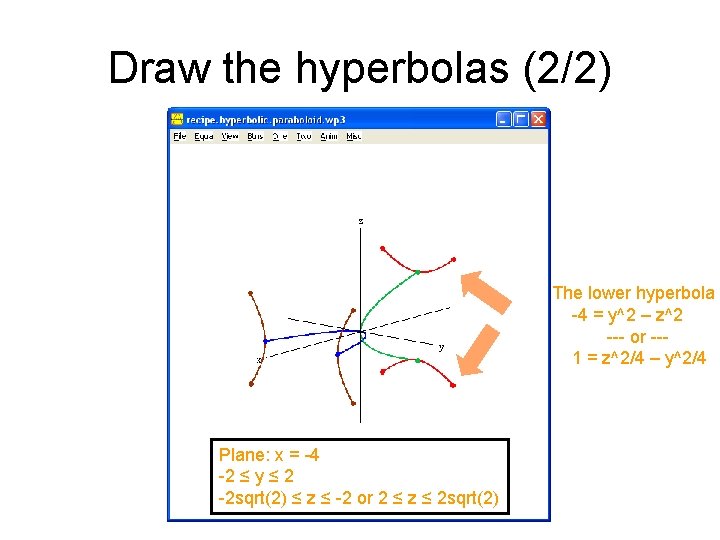
Draw the hyperbolas (2/2) The lower hyperbola -4 = y^2 – z^2 --- or --1 = z^2/4 – y^2/4 Plane: x = -4 -2 ≤ y ≤ 2 -2 sqrt(2) ≤ z ≤ -2 or 2 ≤ z ≤ 2 sqrt(2)

Connect the hyperbolas • Connect the upper hyperbola, upper ends, to the lower hyperbola, upper ends • Connect the upper hyperbola, lower ends, to the lower hyperbola, lower ends • If the two hyperbola arcs are appropriately matched (see the document “An Interesting Property of Hyperbolic Paraboloids”), then these line segments lie on the surface of the hyperbolic paraboloid.
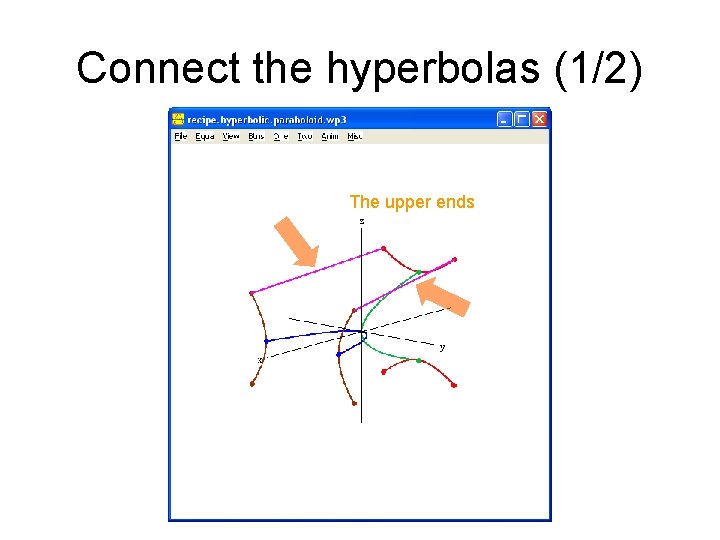
Connect the hyperbolas (1/2) The upper ends
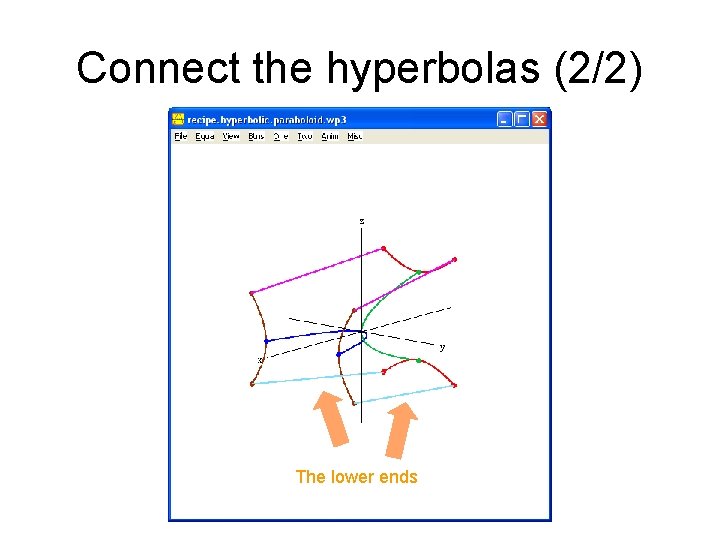
Connect the hyperbolas (2/2) The lower ends
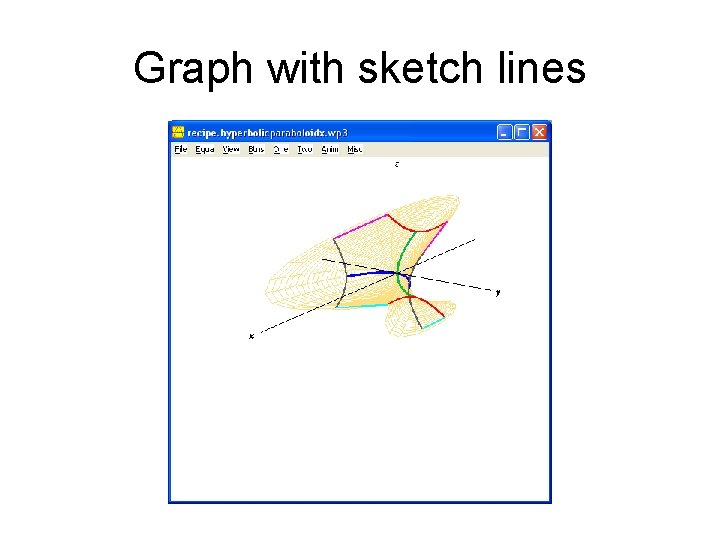
Graph with sketch lines
- Slides: 14