How to calculate when a star a planet

How to calculate when a star, a planet, the moon, or the sun will rise and set* *If you know its right ascension and declination and your latitude and longitude

Notation a = right ascension d = declination f = latitude a=altitude

We make use of spherical trig • The standard formula for the altitude of an object is: sin(a) = sin(d)sin(f) + cos(d) cos(f) cos(H) • If a = 0° (the object is on horizon, either rising or setting), then this equation becomes: cos(H) = - tan(f) tan(d) • This gives the semi-diurnal arc H: the time between the object crossing the horizon, and crossing the meridian. • Knowing the Right Ascension of the object, and its semi-diurnal arc, we can find the Local Sidereal Time of meridian transit, and hence calculate its rising and setting times. • One should put in a correction for atmospheric refraction, but we will neglect it for the moment

East Lansing f = +42. 7 • At this time of year, when does Arcturus rise? Arcturus a = 14 h 14 min +19 D 19’ • cos(H) = - tan(f) tan(d) = -(0. 923)(0. 351) = -0. 324 H =109 degrees In time units H = 109/15 = hours. Arcturus will rise 4. 7 hours before it reaches the meridian and set 7. 3 hours after it passes the meridian. That is, it will rise 7. 3 hours before LST = 14 H 14 M and set 7. 3 hours later than that time.

So when is LST = 14 H 14 M on Jan. 20? • LST at local midnight on Jan. 21 is about 4 x 2 = 8 hours So LST = 14 H 14 M will come at about 6: 13 am local time or 6: 14 +0: 37 EST = 6: 50 am. And we predict that Arcturus will rise at 7. 3 hours before that or at about 11: 30 pm. We’ve neglected refraction and some other small effects.

Let’s calculate when the sun sets • • On Jan. 20 the sun is at a = 20 H 08 M d=-20 D 10’ cos(H) = - tan(f) tan(d) = -(0. 923)(-0. 367) = 0. 339 H = 70. 2/15 = 4. 7 hours. The sun would set at about 4. 7 hours after local noon. Or at about 4 H 42 min + 37 min = 5: 19 pm EST The actual setting time for that date is 5: 36 pm How could we make our calculation more accurate?

Corrections 1. 2. Refraction: varies with your location and even the weather but is about 34 arcmin at the horizon For the sun to set, the top must disappear. Thus even without refraction the center of the sun can be 15 arcmin below the horizon before the top sets: So in the formula sin(a) = sin(d)sin(f) + cos(d) cos(f) cos(H) For a use -34 + 15 = -49’ instead of 0. Then we get -0. 014 = (-0. 345)(0. 678) + (0. 939)(0. 735)cos H so H = 71. 4 or 4 hours 46 min. When we add the 37 minutes that brings our setting time to 5: 23 pm , closer but still early What have we forgotten?

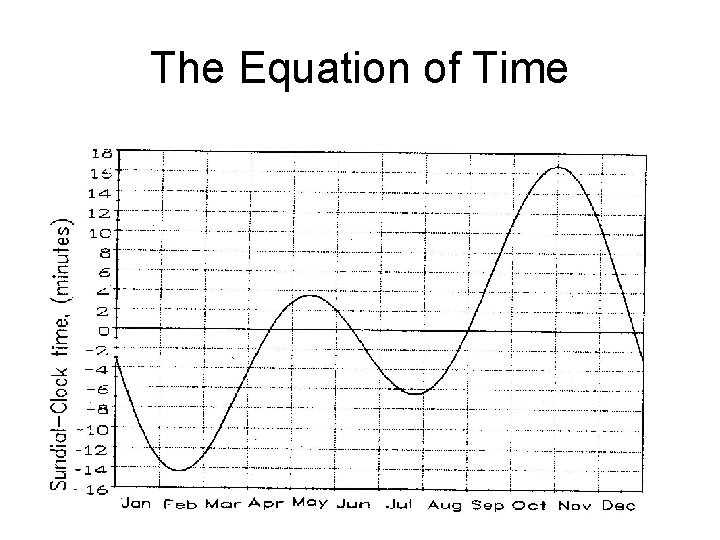
The Equation of Time

Taking account of the equation of time • We find that on Jan. 20 the equation of time is about -12 minutes. That is, apparent solar time is about 12 minutes earlier than mean solar time. When we add 12 minutes to our answer we get 5: 23 + 0: 12 =5: 35 pm Pretty close to the standard value

Celebrations all around!