HOW TO ADD SUBTRACT MULTIPLY DIVIDE POLYNOMIALS MONOMIALS

HOW TO ADD, SUBTRACT, MULTIPLY & DIVIDE POLYNOMIALS (MONOMIALS, BINOMIALS & TRINOMIALS) By: Seth Rockovich

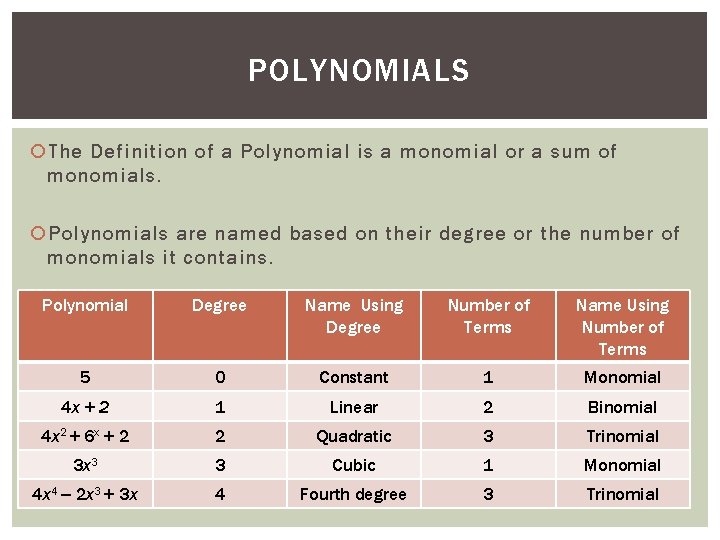
POLYNOMIALS The Definition of a Polynomial is a monomial or a sum of monomials. Polynomials are named based on their degree or the number of monomials it contains. Polynomial Degree Name Using Degree Number of Terms Name Using Number of Terms 5 0 Constant 1 Monomial 4 x + 2 1 Linear 2 Binomial 4 x 2 + 6 x + 2 2 Quadratic 3 Trinomial 3 x 3 3 Cubic 1 Monomial 4 x 4 – 2 x 3 + 3 x 4 Fourth degree 3 Trinomial

MONOMIAL The definition of a Monomial is a real number, a variable, or a product of a real number and one or more variables with wholenumber exponents. An example of a Monomial is: § 17 y -4 z 2 2. 5 xy 2 a 3 The degree of a Monomial is the sum of the exponents of its variable. To find the degree of a Monomial you look at the exponents. Here are examples: § 3 x § 2 x 3 y 2 § 5 Degree=1 Degree=5 Degree=0 3 x=3 x 1 so the exponent is 1. The exponents are 3 and 2; their sum is 5. 5=5 x 0. The degree of a nonzero constant is 0.

BINOMIALS The definition of a Binomial is a Polynomial with exactly two (2) unlike terms. An example of a Binomial is: §x+3 x 2 + 5 x + x 2 2 x + 3 3 x 2 + 2 x The next few are NOT examples of Binomials: § § 3 + 2 (These are not unlike terms) x 2 (This has only 1 expression) x + x (These are not unlike terms) x 2 + 4 x + 5 (This is a trinomial) These are not Binomials!

TRINOMIALS The definition of a Trinomial is a Polynomial with exactly three (3) unlike terms. An example of a Trinomial is: § x 2 + 7 x +10 3 y 2 -5 y +3 -2 xy 2 + 3 xy -8 The next few are NOT examples of Trinomials: § § 3 + 2 + 5 (These are not unlike terms) x 2 + x (This has only 2 expressions) These are not Trinomials! x + x (These are not unlike terms) x 2 + 4 (This is a binomial)

FORMULAS FOR POLYNOMIALS Distributive Property is when you multiply anything in parenthesis by the leading factor.

FORMULAS FOR POLYNOMIALS The Foil Method is a technique for distributing two binomials. The letters stand for: § § First (multiply the terms which occur first in each binomial) Outer (multiply the outermost terms in the product) Inner (multiply the innermost two terms) Last (multiply the terms which occur last in each binomial)

FORMULAS FOR POLYNOMIALS The Box Method is a strategy for multiplying large numbers.

ADDING POLYNOMIALS To add a Polynomial you first need to collect like terms. Ex: (3 x 3 + 2 x 2 – 2 x + 3) + (-2 x 3 + 5 x 2 + 5 x - 1) First find the numbers that have equal x exponents and add them together. 3 x 3 – 2 x 3 = 1 x 3 2 x 2 + 5 x 2 = 7 x 2 -2 x + 5 x = 3 3 – 1 = 2 One can also solve Polynomial addition problems by creating columns. To do this one first separates each factor in the first parenthesis by putting them into columns. Ex: (3 x 3+ 2 x 2 -2 x + 3) + (-2 x 3 + 5 x 2 + 5 x -1) 3 x 3 2 x 2 -2 x 3 5 x 2 5 x 1 Answer: 1 x 3 Answer: 7 x 2 Answer: 3 x Answer: 2

ADDING POLYNOMIALS Example Problems of Adding Polynomials: § 2 x 2 + 4 x 2 =6 x 2 § (9 g 3 + 2 g 2 ) + (7 g 3 + 6 g 2 )= 16 g 3 + 8 g 2 § (6 j 2 – 2 j + 5) + (3 j 2 + 4 j -6) = 9 j 2 + 2 j - 1

SUBTRACTING POLYNOMIALS To subtract a Polynomial one must keep the first parenthesis, change the subtraction sign to an addition sign, and change everything in the second parenthesis. Once this is complete, you collect like terms and solve. Ex: (x 3 + 3 x 2 + 5 x -4) - (3 x 3 -8 x 2 -5 x +6) (x 3 + 3 x 2 + 5 x -4) + (-3 x 3 +8 x 2 +5 x -6) x 3 -3 x 3 = -2 x 3 3 x 2 + 8 x 2 = 11 x 2 5 x + 5 x = 10 x -4 + -6 = -10 Answer: -2 x 3 + 11 x 2 + 10 x -10

SUBTRACTING POLYNOMIALS Example Problems of Subtracting Polynomials: § 8 x 2 - 4 x 2 = 4 x 2 § (9 g 3 + 2 g 2 ) - (7 g 3 + 6 g 2 )= (9 g 3 + 2 g 2 ) + (-7 g 3 -6 g 2 )= 9 g 3 -7 g 3 = 2 g 3 2 g 2 -6 g 2 =-4 g 2 Answer: 2 g 3 – 4 g 2 § (6 j 2 – 2 j + 5) - (3 j 2 + 4 j -6) = (6 j 2 – 2 j + 5) + (-3 j 2 - 4 j +6) 6 j 2 – 3 j 2 = 3 j 2 2 j – 4 j = -2 j 5 + 6 = 11 Answer: 3 j 2 – 2 j + 11

MULTIPLYING POLYNOMIALS To multiply Polynomials you multiply the coefficients then add the exponents. Ex: (3 x 5) (2 x 2) = 6 x 7 To multiply a Monomial and a Trinomial you use the distributive property, multiple the coefficients and add the exponents. -x 3(9 x 4 – 2 x 3 + 7) -x 3(9 x 4 -2 x 3 + 7) = -x 3 (9 x 4) –x 3(-23) –x 3(7) -9 x 3+4 + 2 x 3+3 -7 x 3 -9 x 7 +2 x 6 -7 x 3 To multiply a binomial and a trinomial you use the distributive property, distribute everything in the first parenthesis to the second parenthesis. (x + 1) (x 2 + x + 1) x x 2 = x 3 x x = x 2 x 1= 1 x 1 x 2= 1 x 2 1 x= 1 x 1 1=1 x 3 + x 2 + x + 1= Answer: x 3 + 2 x 2 + 2 x + 1

MULTIPLYING POLYNOMIALS Example Problems of Multiplying Polynomials: § 5 x(6 x 2 + 10) = Answer: 30 x 3 + 50 x § (x – 5) (2 x + 13) 2 x 2 + 13 x – 10 x – 65 Answer: 2 x 2 + 3 x – 65 § (3 x + 5) (5 x 2 + 4 x + 11) 15 x 3 + 12 x 2 + 33 x + 25 x 2 + 20 x + 55 Answer: 15 x 3 + 37 x 2 + 53 x + 55

DIVIDING POLYNOMIALS To divide a polynomial with a monomial you divide each term of the polynomial with the monomial. Ex: 4 x ÷ 8 y = 4 x 2 = 8 x 3 2 3 8 y 24 y When you divide polynomials you may have to factor to find a common factor between the numerator and denominator. 2 ax + 3 b = 2 ax + 3 b c c c When there are no common factors between the numerator and the denominator you can simplify the expression. x 2 -4 x + 3 = (x -3) (x – 1) = x – 1 x – 3 x - 3

DIVIDING POLYNOMIALS Example Problems of Dividing Polynomials: (27 x 3 + 12 x) ÷ 3 x 2 27 x 3 + 12 x 1 = 3 x 2 27 x 3 + 12 x = 9 x 1 + 4 x- 1 = Answer: 9 x + 4 3 x 2 (3 d 2 – 4 d + 13) ÷ (d + 3) 3 d – 13 d +3 √ 3 d 2 - 4 d + 13 3 d 2 + 9 d -13 d + 13 -13 d – 39 52 Answer: 3 d – 13 + 52 d + 3 x Divide 3 d 2 ÷ d = 3 Multiply 3 d(d + 3) = 3 d 2 + 9 Divide -13 d ÷ d = -13 Multiply -13 d(d +3)= -13 d - 39