How science works adapted from Coombs 1983 Empirical

How science works (adapted from Coombs, 1983)
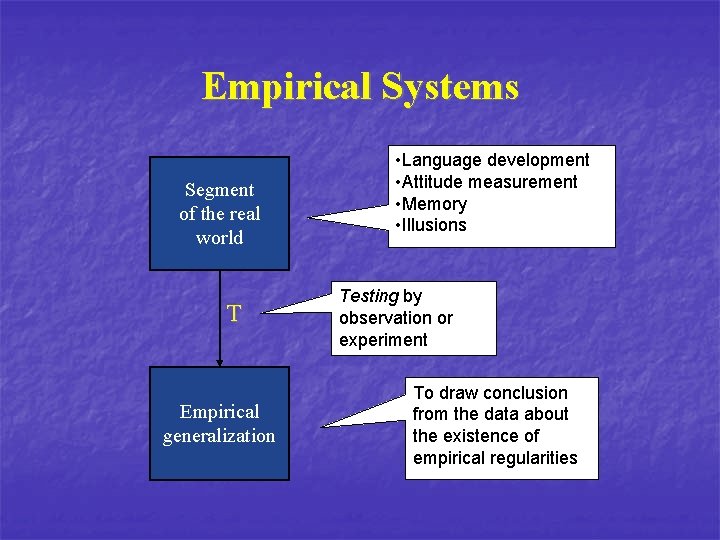
Empirical Systems Segment of the real world T Empirical generalization • Language development • Attitude measurement • Memory • Illusions Testing by observation or experiment To draw conclusion from the data about the existence of empirical regularities
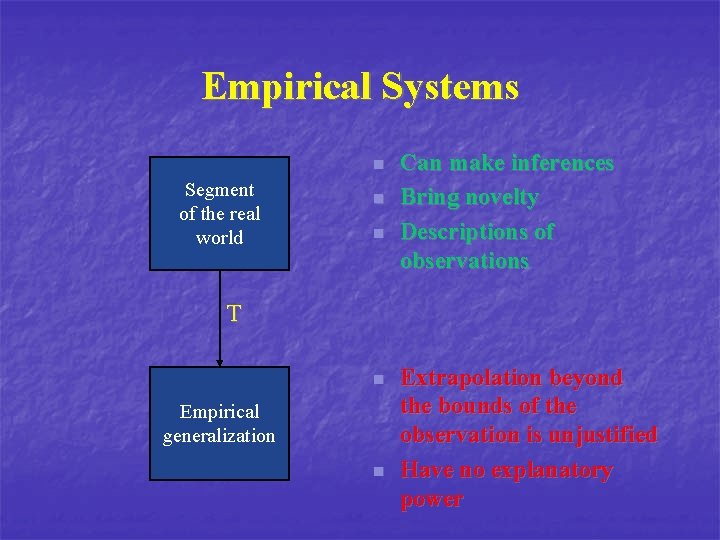
Empirical Systems n Segment of the real world n n Can make inferences Bring novelty Descriptions of observations T n Empirical generalization n Extrapolation beyond the bounds of the observation is unjustified Have no explanatory power
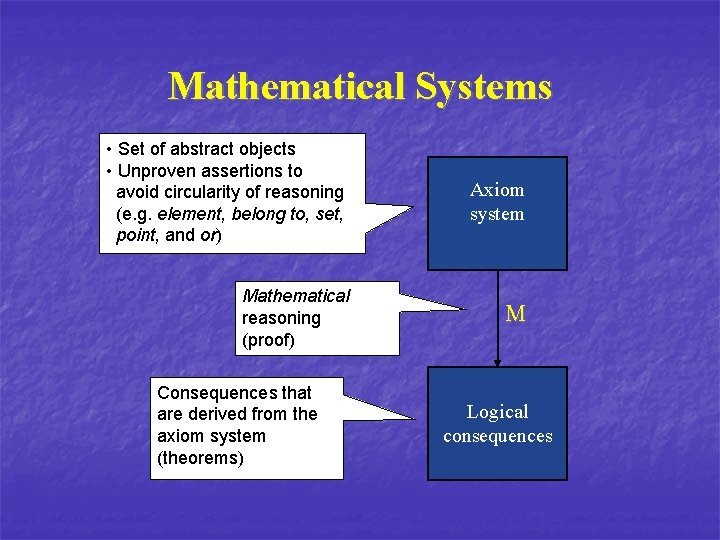
Mathematical Systems • Set of abstract objects • Unproven assertions to avoid circularity of reasoning (e. g. element, belong to, set, point, and or) Mathematical reasoning (proof) Consequences that are derived from the axiom system (theorems) Axiom system M Logical consequences
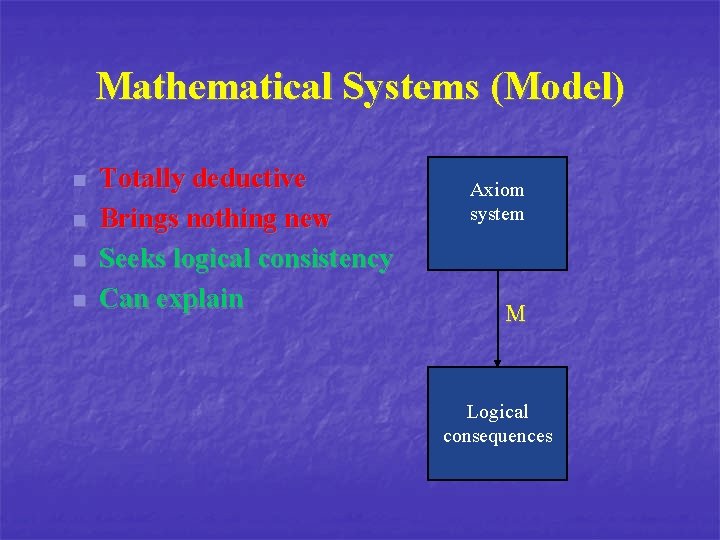
Mathematical Systems (Model) n n Totally deductive Brings nothing new Seeks logical consistency Can explain Axiom system M Logical consequences

Empirical and Mathematical Systems Segment of the real world (abstraction) A T Axiom system M (interpretation) Empirical generalization I Logical consequence
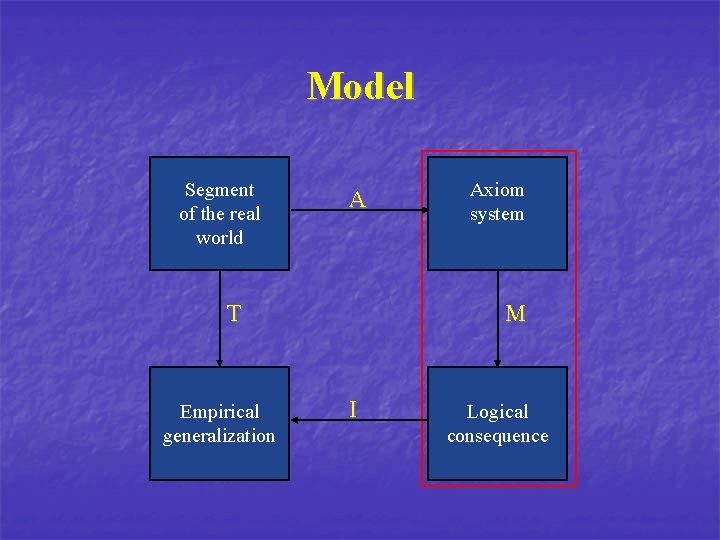
Model Segment of the real world A T Empirical generalization Axiom system M I Logical consequence
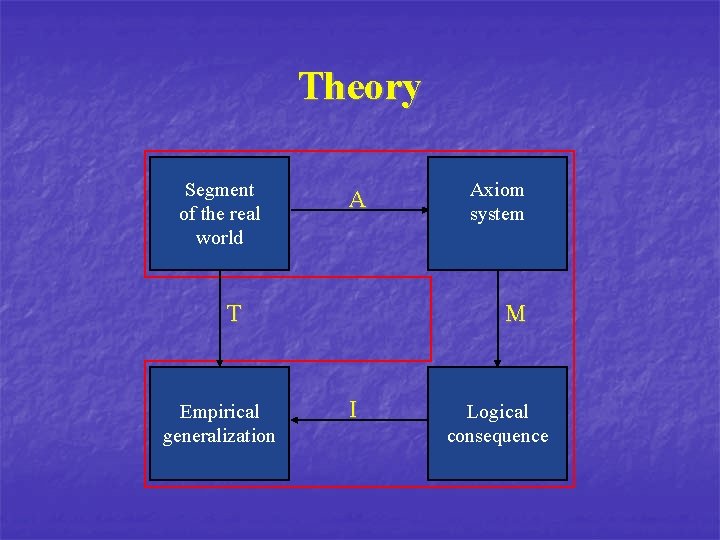
Theory Segment of the real world A T Empirical generalization Axiom system M I Logical consequence

The empirical world is rich, the mathematical world is powerful. The match is fruitful. If AMI = T, then scientific knowledge has increased Segment of the real world A T Empirical generalization Axiom system M I Logical consequence
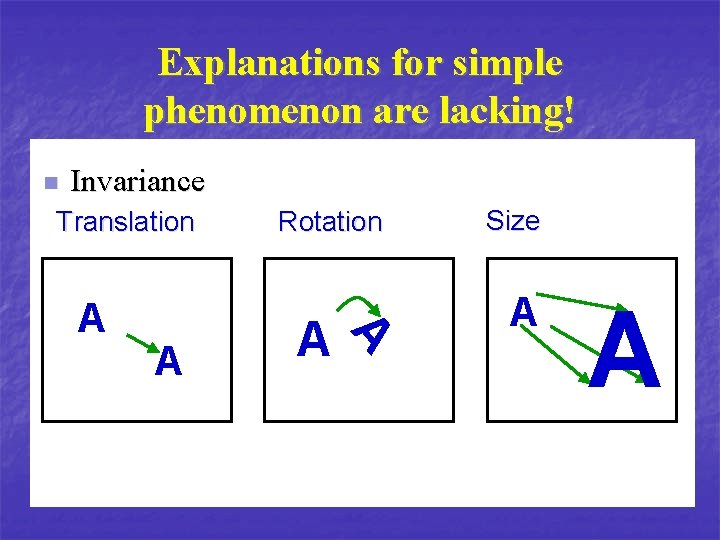
Explanations for simple phenomenon are lacking! n Invariance Translation A A Rotation Size A A
- Slides: 10