How many numbers are there WARNING This deals

How many numbers are there? WARNING: This deals with hazardous doses of infinity!

Remember! In this Power. Point, infinity is showed in many sizes (it has more than one value)! This isn’t about how infinity has many sizes, but about the algebra behind the number of real, whole, and integer numbers there are. For this we will assume that ∞ is how many natural numbers there are (all positive numbers not including 0 eg: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, etc. )

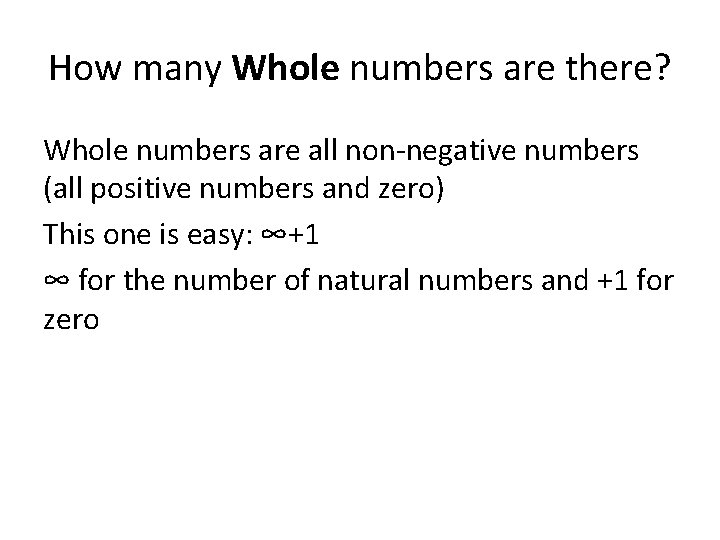
How many Whole numbers are there? Whole numbers are all non-negative numbers (all positive numbers and zero) This one is easy: ∞+1 ∞ for the number of natural numbers and +1 for zero

How many Integers are there? Integers are all of the non-decimal/fraction numbers (eg: 1, 0, 3, -6, 2353) This is a bit harder (but still easy): 2∞+1 2∞ for the negative and positive integers, and +1 for zero

How many Real numbers are there? Real numbers are all numbers (except i and some other 8 -dimensional numbers) This one is hard: (∞∞ )2∞+2∞+1 ∞∞ for all numbers between zero and one, times 2∞ for doing ∞∞ between all of the integers, +2∞ for all of the integers (besides zero), and +1 for zero It could also be: 2(∞∞+1)+2∞+1 (they equal the same thing)

How many numbers are there? •

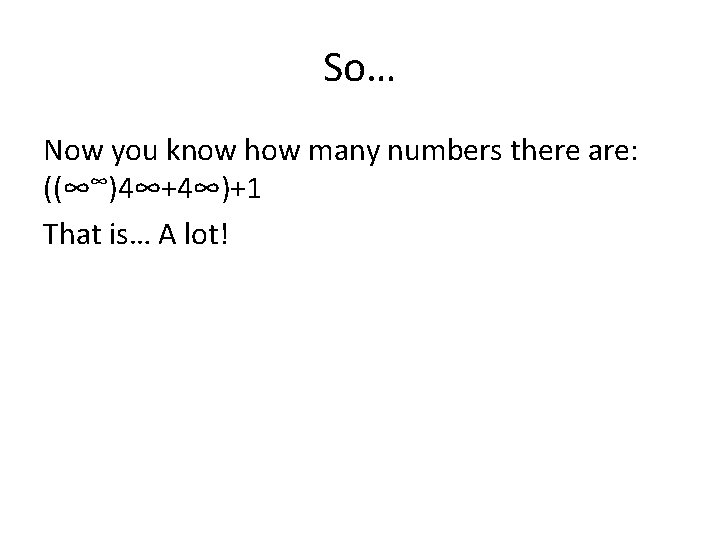
So… Now you know how many numbers there are: ((∞∞)4∞+4∞)+1 That is… A lot!