HOW MANY ELEMENTS How to choose element size

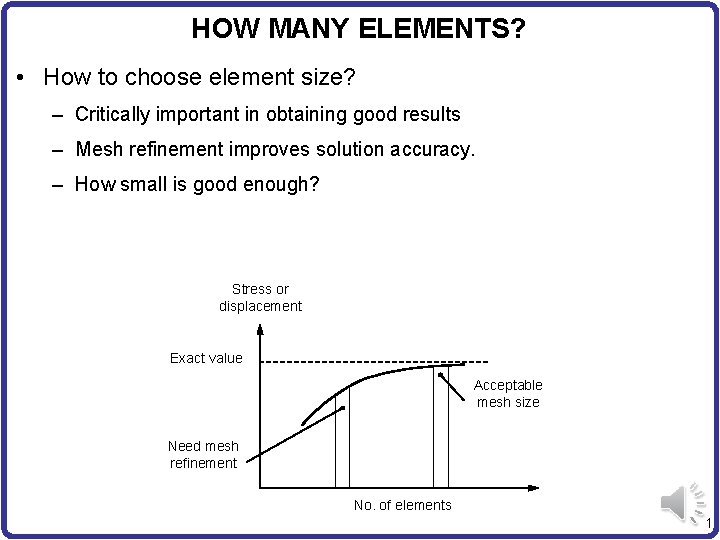
HOW MANY ELEMENTS? • How to choose element size? – Critically important in obtaining good results – Mesh refinement improves solution accuracy. – How small is good enough? Stress or displacement Exact value Acceptable mesh size Need mesh refinement No. of elements 1

HOW MANY ELEMENTS cont. • Convergence rate • Richardson extrapolation – Calculate the function of interest at three different meshes – Let h 1, h 2, and h 3 be the sizes of elements, ordered by h 1 > h 2 > h 3 – Usually h 3=ph 2=p 2 h 1 – Then – Convergence rate a: indicates how fast the solution will converge 2

EXAMPLE • Calculating the maximum stress in an FE model, we used a 2 x 2, 4 x 4, 8 x 8, and 16 x 16 elements. The results are given in the table. Estimate the true maximum stress. For convenience you can assume that the largest h value is 1. Mesh size Max stress 3 x 2 71. 53 6 x 4 75. 63 12 x 8 77. 35 24 x 16 77. 92 • Using first three results get • Using the last three get • To compare g’s need to multiply second one by 21. 593=-7. 762 3

Quiz-like questions • In order to check convergence rate of a 3 D tetrahedral 4 -node element you analyze a problem with an analytical solution giving a maximum stress of 100 ksi. A mesh with 800 elements gives you a stress of 80 ksi, and a mesh with 6400 elements gives you 92 ksi. Calculate the rate of convergence. • For the same data above, assume that you do not know the analytical solution, but you know that the rate of convergence is 2. Estimate the exact solution. • Answers in the notes page 4

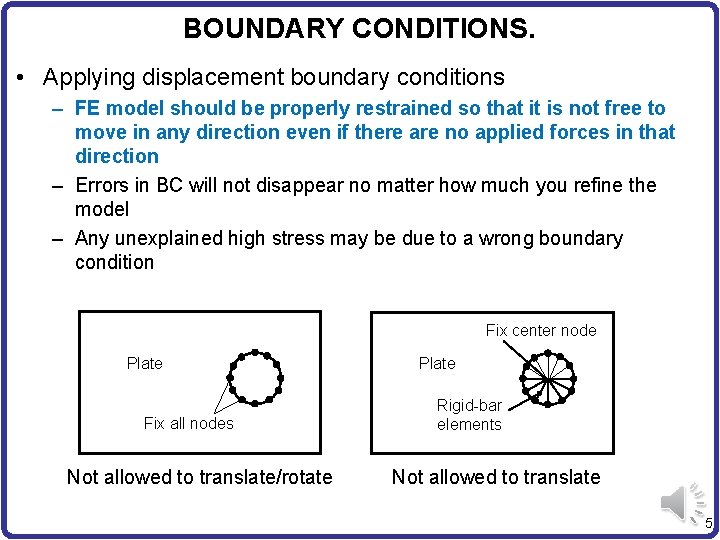
BOUNDARY CONDITIONS. • Applying displacement boundary conditions – FE model should be properly restrained so that it is not free to move in any direction even if there are no applied forces in that direction – Errors in BC will not disappear no matter how much you refine the model – Any unexplained high stress may be due to a wrong boundary condition Fix center node Plate Fix all nodes Not allowed to translate/rotate Plate Rigid-bar elements Not allowed to translate 5

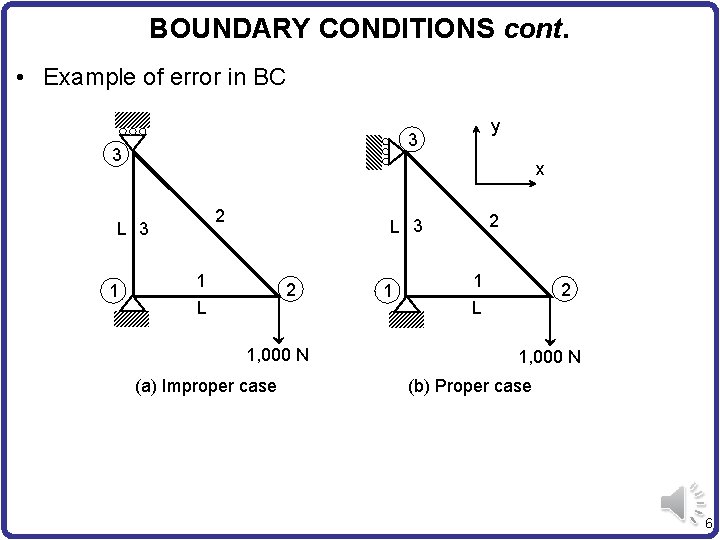
BOUNDARY CONDITIONS cont. • Example of error in BC 3 3 x 2 L 3 1 y 2 L 3 1 L 2 1, 000 N (a) Improper case 1 1 L 2 1, 000 N (b) Proper case 6

APPLIED LOADS • Applying external forces – Forces are applied through a complex mechanism – It is often simplified when the interest region is far from the load application location – FE results near the load application location are not accurate due to approximation involved in the force • Applying a concentrated force – Theoretically infinite stress (zero area) – Practically, all forces are distributed in a region – Concentrated force in FE is an idealization of distributed forces in a small region 7

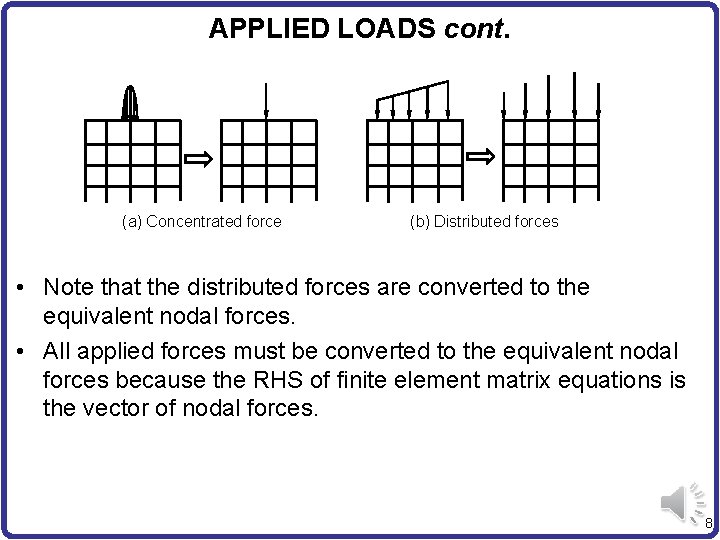
APPLIED LOADS cont. (a) Concentrated force (b) Distributed forces • Note that the distributed forces are converted to the equivalent nodal forces. • All applied forces must be converted to the equivalent nodal forces because the RHS of finite element matrix equations is the vector of nodal forces. 8

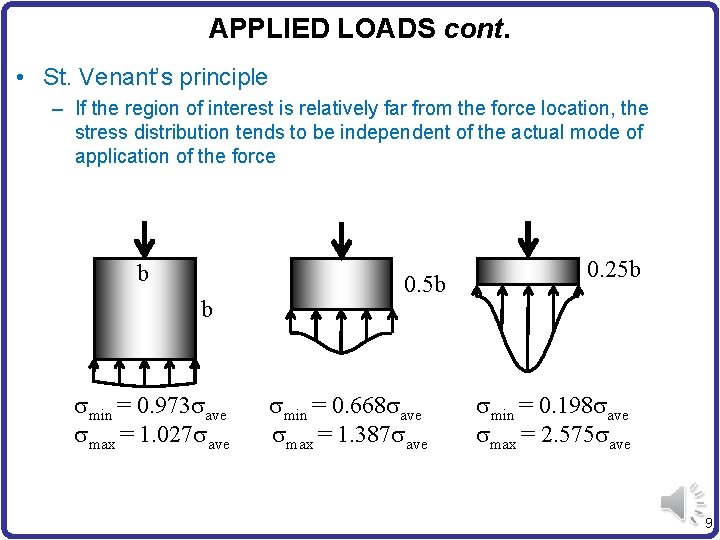
APPLIED LOADS cont. • St. Venant’s principle – If the region of interest is relatively far from the force location, the stress distribution tends to be independent of the actual mode of application of the force b b smin = 0. 973 save smax = 1. 027 save 0. 5 b smin = 0. 668 save smax = 1. 387 save 0. 25 b smin = 0. 198 save smax = 2. 575 save 9

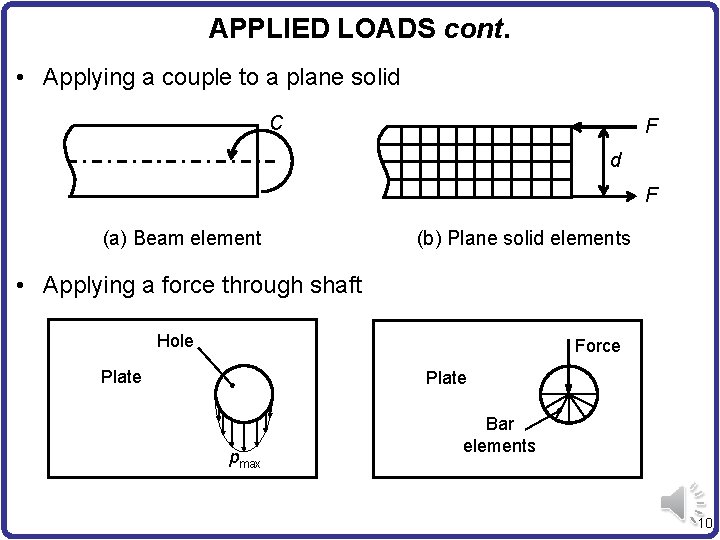
APPLIED LOADS cont. • Applying a couple to a plane solid C F d F (a) Beam element (b) Plane solid elements • Applying a force through shaft Hole Force Plate pmax Bar elements 10

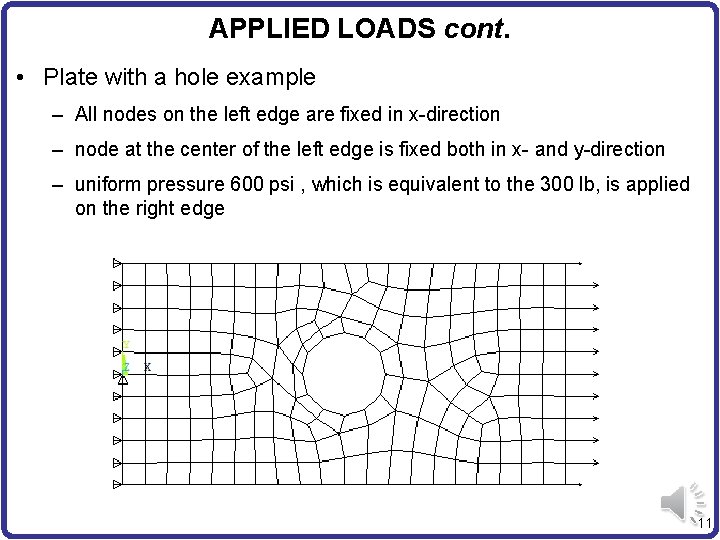
APPLIED LOADS cont. • Plate with a hole example – All nodes on the left edge are fixed in x-direction – node at the center of the left edge is fixed both in x- and y-direction – uniform pressure 600 psi , which is equivalent to the 300 lb, is applied on the right edge 11

Quiz-like questions • What is the implication of the St. Venant principle in terms of how accurately you need to know how loads are applied to a structure? • When a point load is applied, how would the stresses converge as you refine the mesh? • For a 3 D structure, what is the minimum number of degrees of freedom that must be restrained in order for the stiffness matrix of the structure not to be singular? • Answers in the notes page. 12