How Important is the Global Financial Cycle Evidence

How Important is the Global Financial Cycle? Evidence from Capital Flows Eugenio Cerutti, Stijn Claessens and Andrew K. Rose

Q: How Important is Global Financial Cycle for Capital Flows? • Rey and others: very “Risky asset prices around the globe, from stocks to corporate bonds, have a strong common component. So do capital flows … The global financial cycle can be related to monetary conditions in the centre country and to changes in risk aversion and uncertainty … capital flows … are largely driven by a global factor … “ - Rey (2013, pp 1 -2) Rose: Quantifying Global Financial Cycle Effect on Capital Flows 2

Key Finding: Effects of Global Financial Cycle on capital flows just not that important • Plain vanilla approach: conventional techniques, models, metrics • Use capital flow panel dis-aggregated by direction/type, 1990 Q 12015 Q 4, 85 countries • Measure GFCy via: a) observables in central countries (VIX) and b) unobservables (commonality in capital flows, via extracted dynamic factors) • Little evidence of significant, conspicuous GFCy • Using both measures gives upper bound of ≈25% of capital flow variation explained by GFCy • Often much less Rose: Quantifying Global Financial Cycle on Capital Flows 3

Much Interest in Global Financial Cycle (GFCy) Literature • Rey and co-authors (many) • Forbes and Warnock (2012) • Ghosh et al (2014) • Koepke (2015) • Bruno and Shin (2015 a, 2015 b) • Avdjviev et al (2016 a, b) • IMF 2017 Annual Research Conference • RIDGE 2017 Conference Rose: Quantifying Global Financial Cycle on Capital Flows 4

Serious Policy Implications Very synchronized GFCy implies EM policymakers can do little more than insulate their economies (capital controls, macro-prudential, . . . ) and blame US for exogenous shocks: “As capital flows respond to US monetary policy, they may not be appropriate for the cyclical conditions of many economies. . . ” - Rey (2015, pp 9 -10) Rose: Quantifying Global Financial Cycle on Capital Flows 5

Identifying GFCy: Empirical Strategy • GFCy intrinsically unobservable • Guiding idea: if GFCy consequential, should drive high proportion of fluctuations in most types of capital flows (and domestic credit creation, asset prices, . . . ) in many places, much of the time • High commonality in financial conditions, manifest in capital flows, driven by observable global determinants • The initial motivation: if the GFCy is so obviously important, why didn’t we already know about it? • Plain vanilla approach: model, data, estimation, metrics …. Rose: Quantifying Global Financial Cycle on Capital Flows 6

Two Approaches to Measuring GFCy 1. (Direct) Examine observable “fundamental” GFCy drivers, centercountry macro/financial determinants of capital flows • Which variables? • Which center countries? • Literature delivers consensus (VIX), but check with many variables, countries 2. (Indirect) Examine observable commonality via factors • Extract common dynamic factors (following Rey) • Attribute all commonality to GFCy to be conservative, establish upper bound for GFCy impact • Ignore correlated shocks bc commodity price movements, sunspots, contagion, etc. Rose: Quantifying Global Financial Cycle on Capital Flows 7

Fundamentals: Volatility • VIX as consensus • Ticker symbol for CBOE implied near-term volatility of S&P 500 index options (end of quarter) • Used extensively in literature: e. g. , Passari and Rey (2015, p 683) VIX as “our proxy for the global financial cycle. . . Large gross cross-border flows are moving in tandem across countries regardless of the exchange rate regime, they tend to rise in periods of low volatility and risk aversion and decrease in periods of high volatility and risk aversion, as measured by the VIX…” • Also used by Cerutti, Claessens, and Ratnovski (2017), Obstfeld et al. (2017), Advjiev et al. (2016), Bruno and Shin (2015 a, b), Fratzscher (2012), Forbes and Warnock (2012). . . • Robustness: use VDAX (Germany), VSTOXX (EMU), IVI (UK) Rose: Quantifying Global Financial Cycle on Capital Flows 8

Fundamentals, continued • Use seven other fundamentals for sensitivity analysis as well 1. 2. 3. 4. 5. 6. 7. Nominal policy interest rate (Fed. Funds/UK Base/Euro Area deposit) Ex post real rate (using realized CPI inflation) TED spread (3 -m LIBOR – government rate) Yield curve slope (10 yr – 3 m government rates) GDP growth Real effective (CPI) exchange rate growth (Shin) M 2 growth • Default center-economy is USA • Use UK, EMU for sensitivity analysis Rose: Quantifying Global Financial Cycle on Capital Flows 9

Capital Flow Data: Also Conventional Balance of Payments Series, 1990 Q 1 -2015 Q 4, 85 countries (with gaps) • Usually focus on 63 “small” countries • Exclude US, UK, actual/future EMU members, Japan • Two directions (in/out) • Gross inflows/outflow: net transactions by foreigners/domestic residents • Different types • Foreign Direct Investment (FDI) • Portfolio Equity • Portfolio Debt • Sometimes aggregate portfolio equity and debt as “Portfolio” • Bank Credit (subset of “other investment liabilities, of which borrowers are banks”) Rose: Quantifying Global Financial Cycle on Capital Flows 10

Factors: Measuring Capital Flow Commonality • Create 180 common factors to ensure insensitivity • • • 2 time spans (start 1990 Q 1 and 1996 Q 1; end 2015 Q 4) 3 sets of countries (advanced/emerging/both) 2 directions (in/out) 4 major types (FDI/debt/equity/credit) (also: portfolio≡debt+equity) 3 estimators • Dynamic factor with 1 lag, extract largest eigenvalue factor (Miranda Agrippino-Rey) • Ditto, with 2 lags • Traditional static factor • Ex: use dynamic factor analysis to extract a factor from fifteen emerging markets over 1990 Q 1 -2015 Q 4 for FDI inflows • Include this in FDI inflow equations below Rose: Quantifying Global Financial Cycle on Capital Flows 11

(National) Capital Flow Equations • Panel regressions in paper indicate national heterogeneity • So estimate disaggregate capital flow equations (over time) with LS: CAPFLOWd, e, i, t = Σβij. USFUNDjt + Σγk. FACd, ekt + φi + εd, e, i, t for country i • Regressand: capital flows (% GDP) for direction/type/country • GFCy Regressors: • [Direct] Eight fundamentals (VIX, nominal and real rates, …) • [Indirect] Two factors for relevant capital flow (advanced/emerging) • By Design: ignore dynamics, national demand/supply shocks • Deliberately attribute all fit to GFCy Rose: Quantifying Global Financial Cycle on Capital Flows 12

(National) Capital Flow Equations, continued • Rose: Quantifying Global Financial Cycle on Capital Flows 13
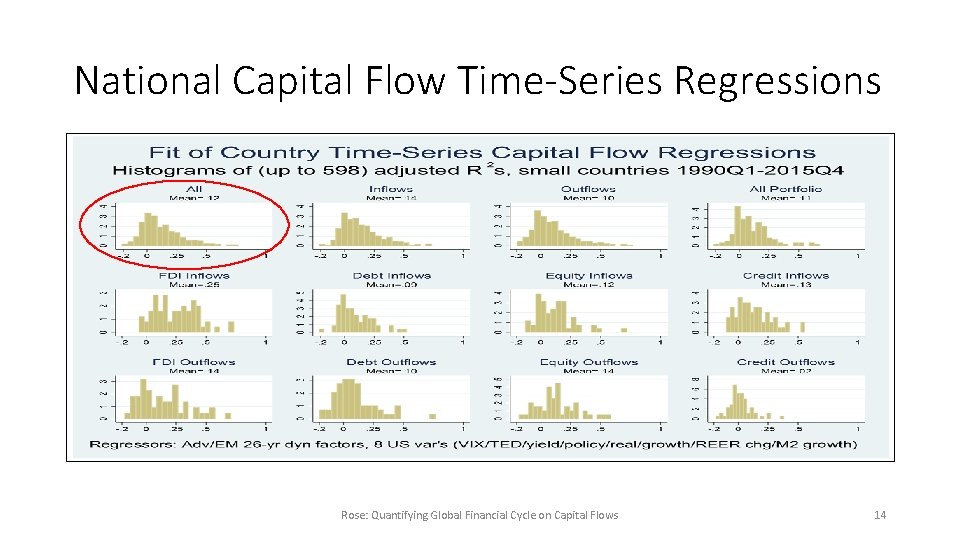
National Capital Flow Time-Series Regressions Rose: Quantifying Global Financial Cycle on Capital Flows 14
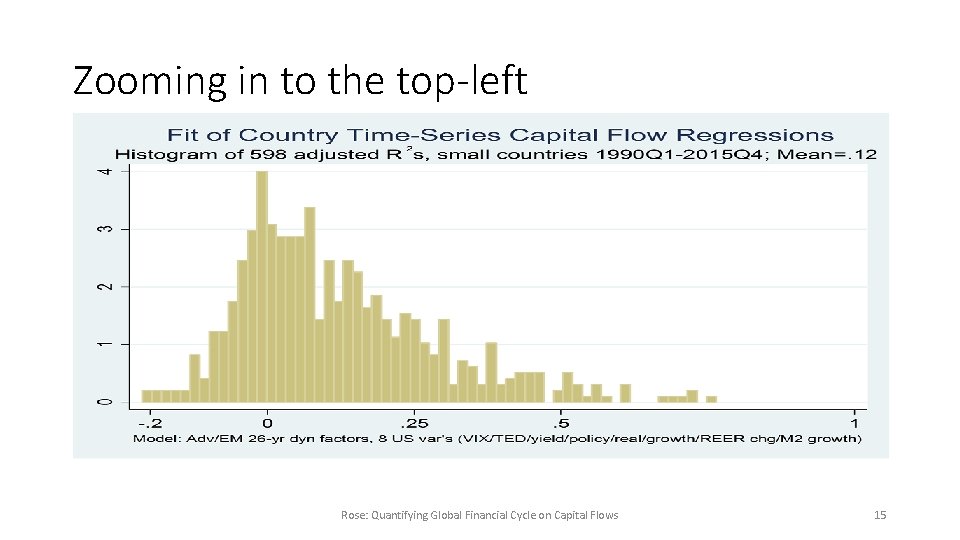
Zooming in to the top-left Rose: Quantifying Global Financial Cycle on Capital Flows 15

Sensitivity Analysis • Rose: Quantifying Global Financial Cycle on Capital Flows 16
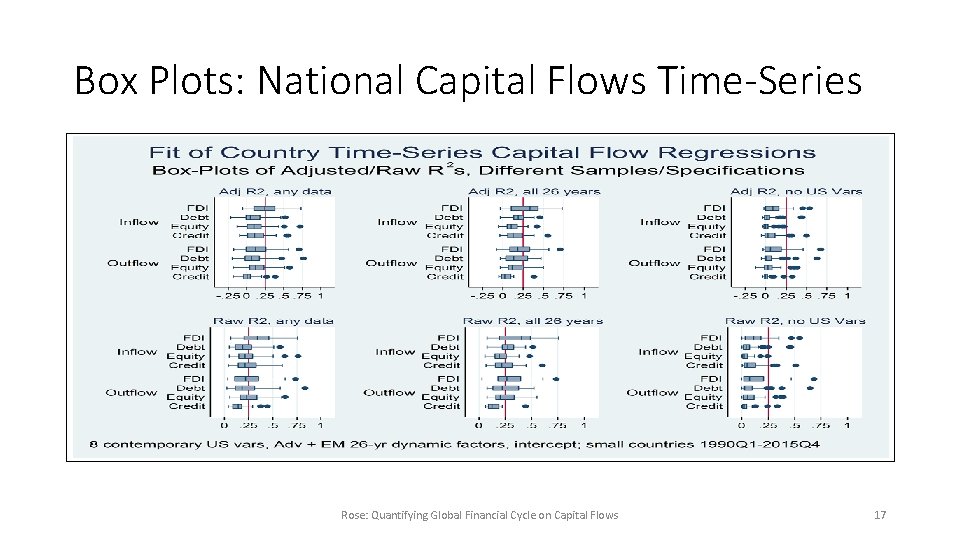
Box Plots: National Capital Flows Time-Series Rose: Quantifying Global Financial Cycle on Capital Flows 17

Different Specifications Rose: Quantifying Global Financial Cycle on Capital Flows 18
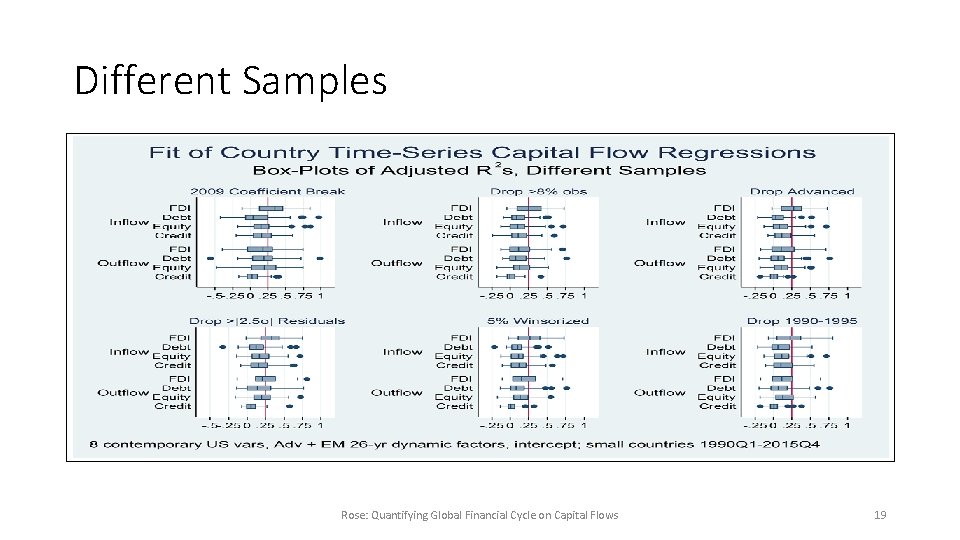
Different Samples Rose: Quantifying Global Financial Cycle on Capital Flows 19
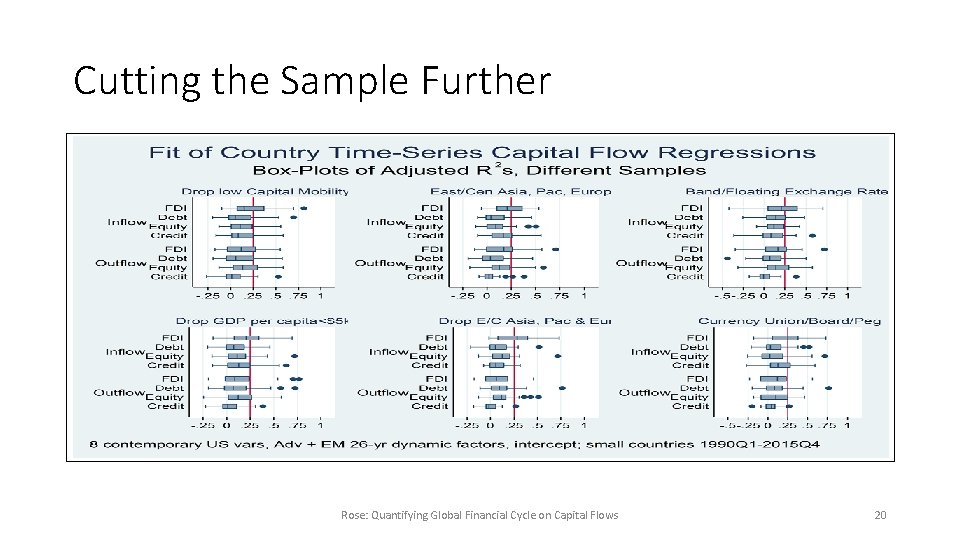
Cutting the Sample Further Rose: Quantifying Global Financial Cycle on Capital Flows 20

Summary • Focus here: quantifying importance of GFCy for capital flows • Coming soon: credit growth, asset prices • Panel regressions, national capital flow equations, event studies • Plain vanilla approach: data, statistical metrics, models, techniques • Measure GFCy both directly and indirectly • Up to eight fundamentals for three large economies, though focus on VIX • Also. . . commonality, extracted from dynamic factor models • Conservative approach • All explanatory power attributed to GFCy • Ignore coefficient signs, sizes (usual focus). . . which are often bizarre (Table A 3) • Poor fit; typically < 25% variation explained, often much less! • Can find exceptions, but they are … exceptions Rose: Quantifying Global Financial Cycle on Capital Flows 21

Conclusion • Global Financial Cycle simply not that important in understanding capital flows • Capital flows of peripheral countries explained by idiosyncratic phenomena • If foreign: difficult to put in place systematic policies to screen “good” from “bad” capital flows • If domestic (likely): periphery country needs to take ownership • Harder to blame center countries for volatility if does not stem from center • Caveat: GFCy can appear elsewhere (e. g. asset prices and credit) • Our future research Rose: Quantifying Global Financial Cycle on Capital Flows 22

Auxiliary Material

More Motivation “There is a global financial cycle in capital flows, asset prices, and in credit growth. This cycle co-moves with the VIX, a measure of uncertainty and risk aversion of the markets. ” - Rey (2013, abstract) “Large gross cross-border flows are moving in tandem across countries regardless of the exchange rate regime, they tend to rise in periods of low volatility and risk aversion and decrease in periods of high volatility and risk aversion, as measured by the VIX … There is a global financial cycle. ” -Passari and Rey (2015, p 693) Rose: Quantifying Global Financial Cycle on Capital Flows 24

External Influences and the Blame Game • Consider something important, driven by exogenous external effects • Flight delays (≡ scheduled-actual arrival time) Flight delays • Linear models (with LARGE data sets) of flight delays often include: • • Flight distance Airline (carrier) effects Time Effects : Hour (both departure and arrival), Day, and Month Controls for conditions at both destination and arrival airports: • • Airport traffic (incoming/outgoing) Visibility Temperature Precipitation • A typical such model has R 2 <<. 2! • But airlines often blame such forces for delays Rose: Quantifying Global Financial Cycle on Capital Flows 25
Country List Argentina Armenia Australia 3, 5 Austria 1 Azerbaijan Bangladesh Belarus Belgium 1 Bolivia Brazil 4, 5 Bulgaria Colombia Costa Rica Croatia Cyprus 1 Czech Republic Denmark Ecuador Estonia 1 Finland 1 France 1 Georgia Hungary Iceland 3 Indonesia 4, 5 Ireland 1 Israel Italy 1 Japan 2 Jordan Kazakhstan Korea 4, 5 Kyrgyzstan Lithuania 1 Luxembourg 1 Macedonia Malta 1 Mauritius Mexico 4, 5 Moldova Mongolia Namibia Netherlands 1 New Zealand 3 Paraguay Peru Philippines 4 Poland 4 Portugal 1 Romania Russia 4, 5 Slovakia 1 Slovenia 1 South Africa 4 Spain 1 Thailand 4 Turkey 4, 5 Uganda Ukraine UK 2 USA 2 Uruguay Venezuela Viet Nam Zambia 1: EMU Cabo Verde Germany 1 Laos Nicaragua Sri Lanka 2: Other Large Canada 3, 5 Greece 1 Latvia 1 Norway 3 Suriname 3: Adv Factor Chile 4 Honduras Lebanon Pakistan Sweden 3 4: EM Factor China 4 Hong Kong Lesotho Panama Switzerland 5 5: Adv/EM Fac Rose: Quantifying Global Financial Cycle on Capital Flows 26
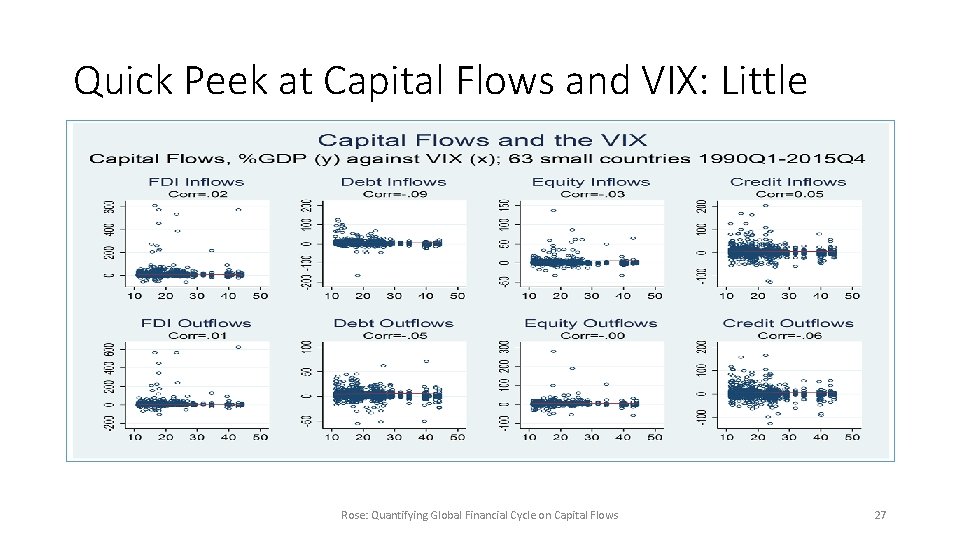
Quick Peek at Capital Flows and VIX: Little Rose: Quantifying Global Financial Cycle on Capital Flows 27

(Interestingly) Dismal Factor Results • If GFCy drives most variation in types/directions of capital flows, then 8 factors should be strongly related • If VIX highly correlated with GFCy, it should also be correlated with factors • BUT THEY’RE NOT! Consider Advanced Economy Factors • Most scatters are simply clouds • VIX not linked to factors • • 3/8 correlations negative; all <. 5 3/8 correlation coefficients significantly different from zero, 2 >0, 1 < 0 FDI inflows the strongest Insensitive results (robustness in paper) Rose: Quantifying Global Financial Cycle on Capital Flows 28
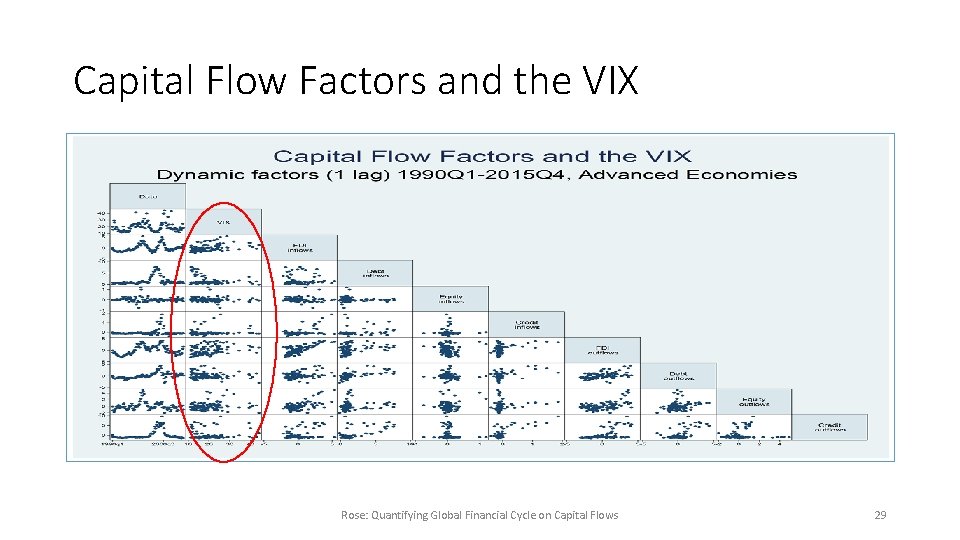
Capital Flow Factors and the VIX Rose: Quantifying Global Financial Cycle on Capital Flows 29

Factors of Advanced, Emerging Countries • Typically very loose relationship • Again, exception is FDI inflows Rose: Quantifying Global Financial Cycle on Capital Flows 30

Advanced and Emerging Economies Rose: Quantifying Global Financial Cycle on Capital Flows 31
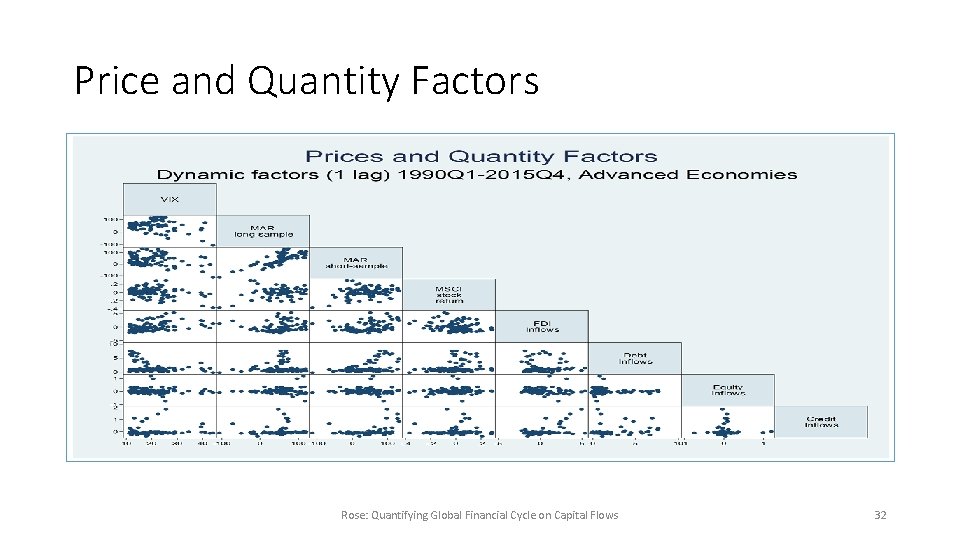
Price and Quantity Factors Rose: Quantifying Global Financial Cycle on Capital Flows 32

Price Factors and Fear Measures • Also loose relationships Rose: Quantifying Global Financial Cycle on Capital Flows 33
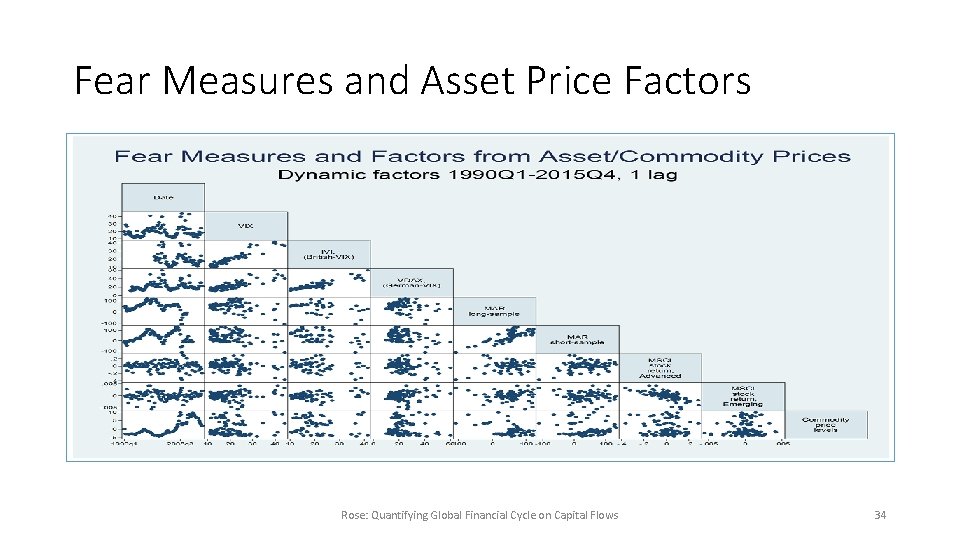
Fear Measures and Asset Price Factors Rose: Quantifying Global Financial Cycle on Capital Flows 34

Capital Flow Panel Regressions • Pool observations across countries • Disaggregate by direction, type • Start without any time-varying regressors, just time fixed effects • Gives upper bound on all possible global phenomena (including GFCy) • Estimate: CAPFLOWd, e, i, t = {φi} + {θt} + εd, e, i, t • Capital flows as % GDP, disaggregated by: • • Direction (d) – in/out Type (e) – FDI/equity/debt/credit Country (i) Quarter (t) Rose: Quantifying Global Financial Cycle on Capital Flows 35
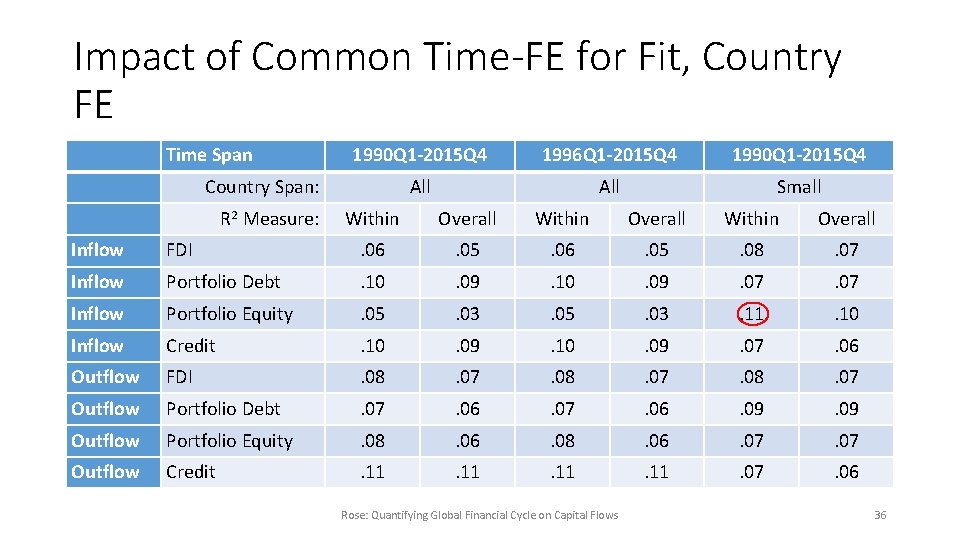
Impact of Common Time-FE for Fit, Country FE Time Span Country Span: R 2 Measure: 1990 Q 1 -2015 Q 4 1996 Q 1 -2015 Q 4 1990 Q 1 -2015 Q 4 All Small Within Overall Inflow FDI . 06 . 05 . 08 . 07 Inflow Portfolio Debt . 10 . 09 . 07 Inflow Portfolio Equity . 05 . 03 . 11 . 10 Inflow Credit . 10 . 09 . 07 . 06 Outflow FDI . 08 . 07 Outflow Portfolio Debt . 07 . 06 . 09 Outflow Portfolio Equity . 08 . 06 . 07 Outflow Credit . 11 . 07 . 06 Rose: Quantifying Global Financial Cycle on Capital Flows 36

Capital Flow Panel Regressions, results CAPFLOWd, e, i, t = {φi} + {θt} + εd, e, i, t • Fits poor for all directions/types of capital flow using within/overall R 2 • Insensitive to time sample/country size • Global phenomena unimportant if impact on all countries identical Rose: Quantifying Global Financial Cycle on Capital Flows 37

But. . . 2 big restrictions implicit 1. No explicit modelling of any economic/financial shocks (e. g. , GFCy) 2. Assumed homogeneity of responses of all countries capital flows to common shocks • Unpack these assumptions in two steps Rose: Quantifying Global Financial Cycle on Capital Flows 38

Model GFCy directly and indirectly • Remove time FE, replace with 8 standard American “push” regressors • a) VIX; b) real GDP growth rate; c) nominal policy rate; d) real policy rate; e) TED spread; f) yield curve slope; g) REER change; and h) M 2 growth • Add dynamic factors (match direction/type of capital flow to regressand) • Attributes all commonality to GFCy • Two factors: advanced, emerging market • Include country FE • But maintain common response (across countries) to 10 regressors: CAPFLOWd, e, i, t = Σβj. USFUNDjt + Σγk. FACd, ekt + {φi} + εd, e, i, t Rose: Quantifying Global Financial Cycle on Capital Flows 39
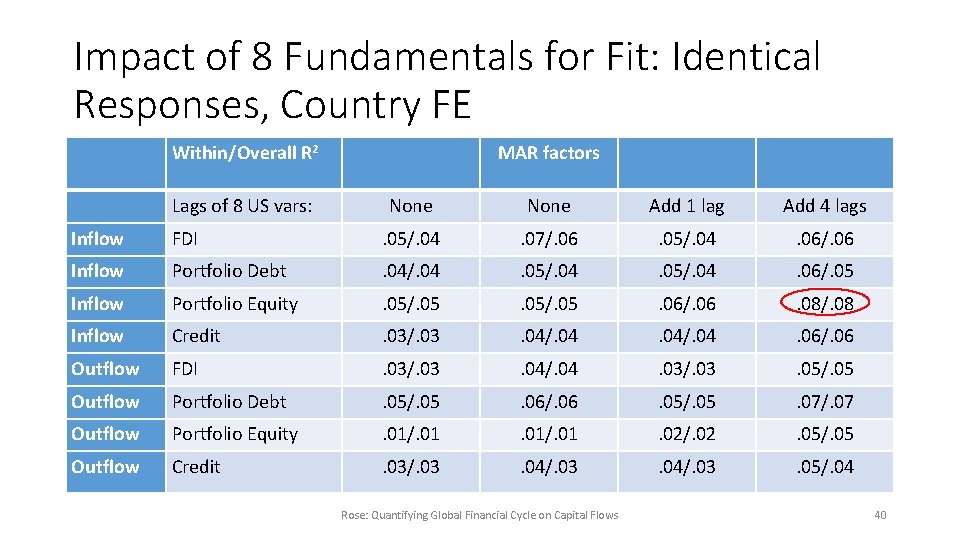
Impact of 8 Fundamentals for Fit: Identical Responses, Country FE Within/Overall R 2 MAR factors Lags of 8 US vars: None Add 1 lag Add 4 lags Inflow FDI . 05/. 04 . 07/. 06 . 05/. 04 . 06/. 06 Inflow Portfolio Debt . 04/. 04 . 05/. 04 . 06/. 05 Inflow Portfolio Equity . 05/. 05 . 06/. 06 . 08/. 08 Inflow Credit . 03/. 03 . 04/. 04 . 06/. 06 Outflow FDI . 03/. 03 . 04/. 04 . 03/. 03 . 05/. 05 Outflow Portfolio Debt . 05/. 05 . 06/. 06 . 05/. 05 . 07/. 07 Outflow Portfolio Equity . 01/. 01 . 02/. 02 . 05/. 05 Outflow Credit . 03/. 03 . 04/. 03 . 05/. 04 Rose: Quantifying Global Financial Cycle on Capital Flows 40

Center-Country Variables explain little variation in capital flows • But above maintains assumption that responsiveness identical across countries • So, add country-specific effects of US variables (possibly at lag s) on capital flows: CAPFLOWd, e, i, t = Σβij, s. USFUNDjt-s + Σγk. FACd, ekt + {φi} + εd, e, i, t Rose: Quantifying Global Financial Cycle on Capital Flows 41
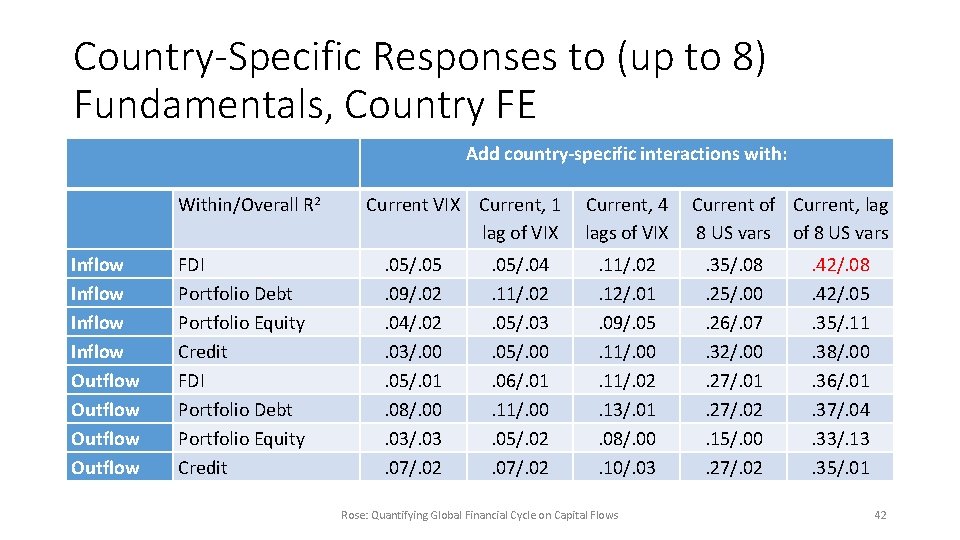
Country-Specific Responses to (up to 8) Fundamentals, Country FE Add country-specific interactions with: Within/Overall R 2 Inflow Outflow FDI Portfolio Debt Portfolio Equity Credit Current VIX Current, 1 Current, 4 Current of Current, lag of VIX lags of VIX 8 US vars of 8 US vars. 05/. 05. 09/. 02. 04/. 02. 03/. 00. 05/. 01. 08/. 00. 03/. 03. 07/. 02 . 05/. 04. 11/. 02. 05/. 03. 05/. 00. 06/. 01. 11/. 00. 05/. 02. 07/. 02 . 11/. 02. 12/. 01. 09/. 05. 11/. 00. 11/. 02. 13/. 01. 08/. 00. 10/. 03 Rose: Quantifying Global Financial Cycle on Capital Flows . 35/. 08. 25/. 00. 26/. 07. 32/. 00. 27/. 01. 27/. 02. 15/. 00. 27/. 02 . 42/. 08. 42/. 05. 35/. 11. 38/. 00. 36/. 01. 37/. 04. 33/. 13. 35/. 01 42

Better, but not Good • VIX alone does little, even when lags included • Need 8 fundamentals (plus lags) • Still fits poor. . . all R 2 s <<. 5 • Profligate parameterization: best fit is within R 2. 42, but only 5. 8 (=2016/349) observations per coefficient, overall R 2 of. 08! Rose: Quantifying Global Financial Cycle on Capital Flows 43

What About Extreme Events? • Forbes and Warnock (2012) select extreme values of capital flows: • • Capital Flight (increased outflow) Retrenchment (decreased outflow) Stop (decreased inflow) Surge (increased inflow) – also studied by Ghosh et al (2014) Rose: Quantifying Global Financial Cycle on Capital Flows 44
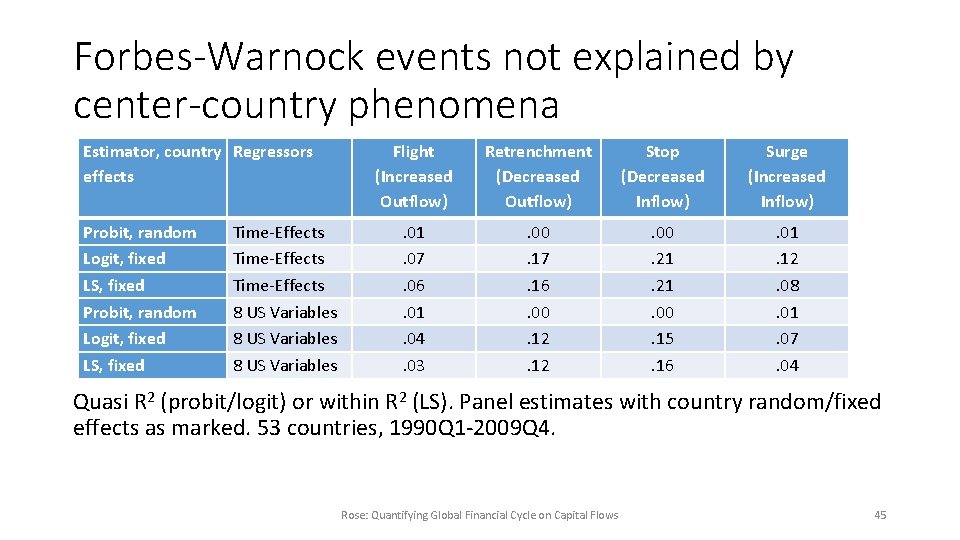
Forbes-Warnock events not explained by center-country phenomena Estimator, country Regressors effects Probit, random Logit, fixed LS, fixed Time-Effects 8 US Variables Flight (Increased Outflow) Retrenchment (Decreased Outflow) Stop (Decreased Inflow) Surge (Increased Inflow) . 01. 07. 06. 01. 04. 03 . 00. 17. 16. 00. 12 . 00. 21. 00. 15. 16 . 01. 12. 08. 01. 07. 04 Quasi R 2 (probit/logit) or within R 2 (LS). Panel estimates with country random/fixed effects as marked. 53 countries, 1990 Q 1 -2009 Q 4. Rose: Quantifying Global Financial Cycle on Capital Flows 45

Domestic Credit Growth: like Capital Flows • Just a peek at preliminary results; more on credit growth and asset prices to come (in separate paper) Rose: Quantifying Global Financial Cycle on Capital Flows 46
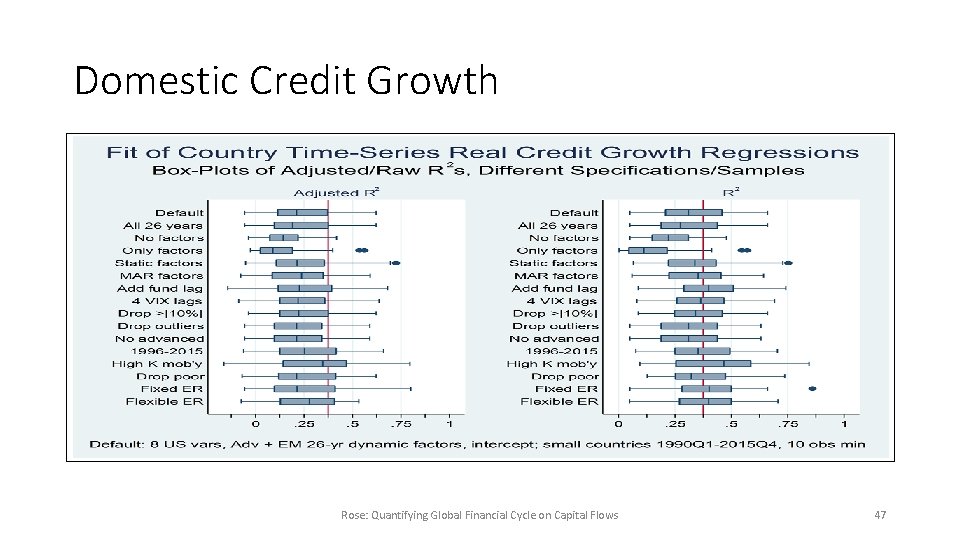
Domestic Credit Growth Rose: Quantifying Global Financial Cycle on Capital Flows 47

Suppose GFCy only Relevant during Crises? • Little suggestion in literature, but. . . • Focus on events when VIX high • 8 occasions when VIX closes above 30 • 6 year event study • Means with empirical (5, 95) confidence intervals • Little evidence of significant shifts around crisis periods • Results insensitive to exact definition of crises (see paper) Rose: Quantifying Global Financial Cycle on Capital Flows 48
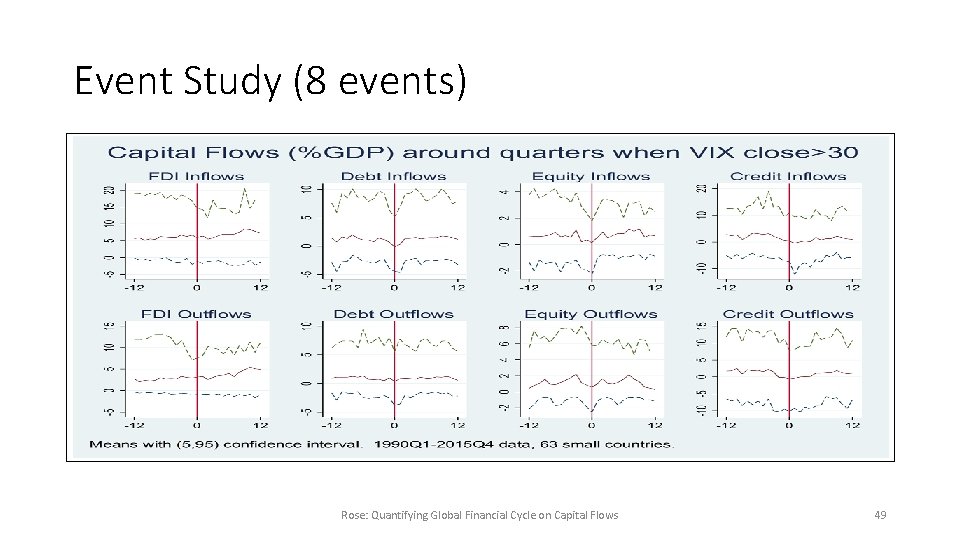
Event Study (8 events) Rose: Quantifying Global Financial Cycle on Capital Flows 49
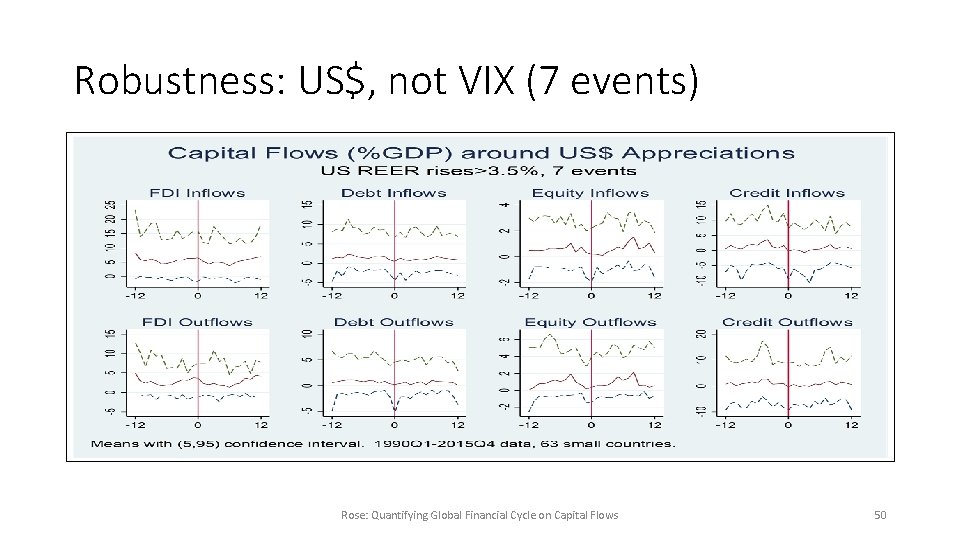
Robustness: US$, not VIX (7 events) Rose: Quantifying Global Financial Cycle on Capital Flows 50
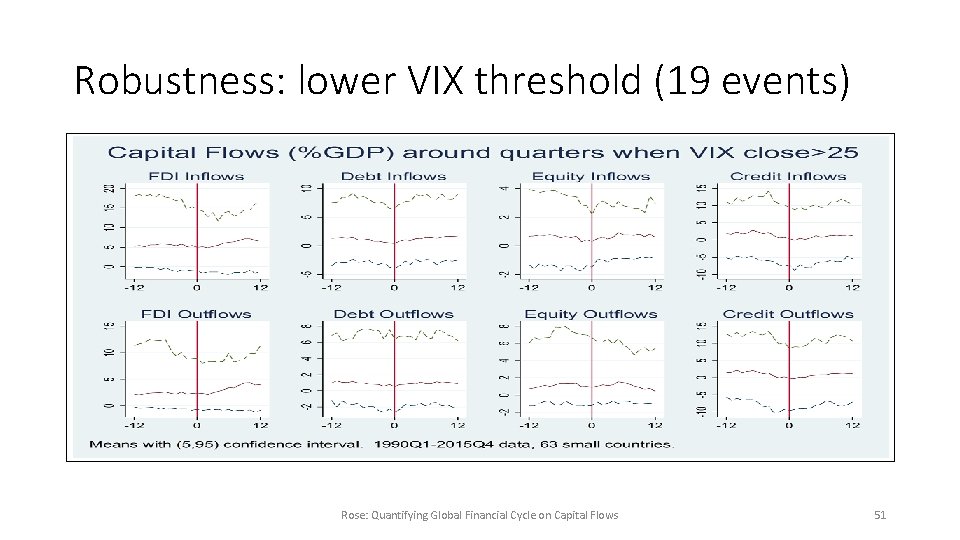
Robustness: lower VIX threshold (19 events) Rose: Quantifying Global Financial Cycle on Capital Flows 51
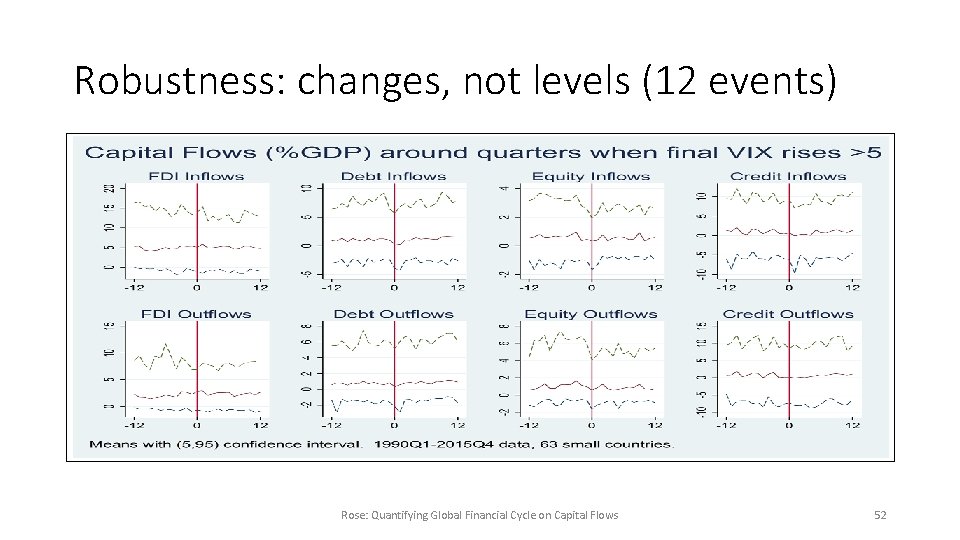
Robustness: changes, not levels (12 events) Rose: Quantifying Global Financial Cycle on Capital Flows 52
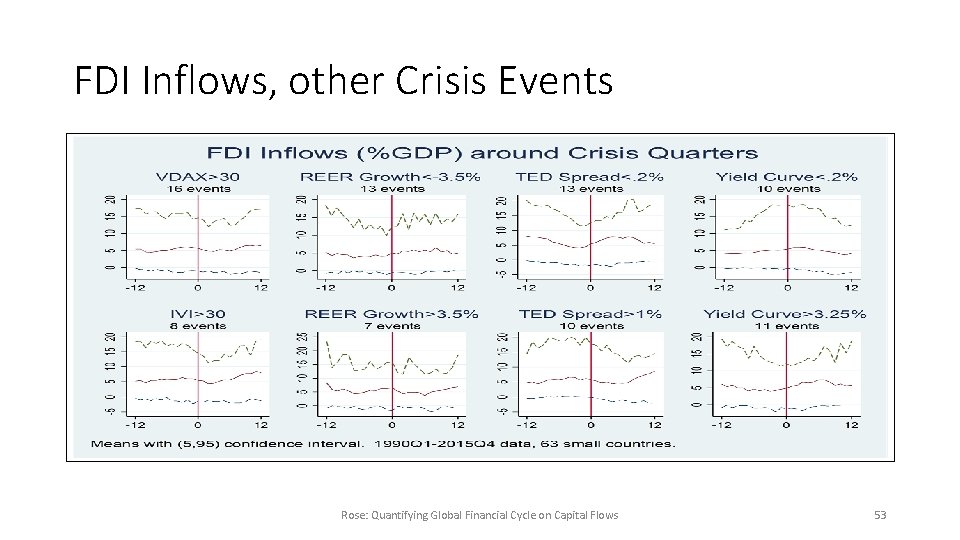
FDI Inflows, other Crisis Events Rose: Quantifying Global Financial Cycle on Capital Flows 53
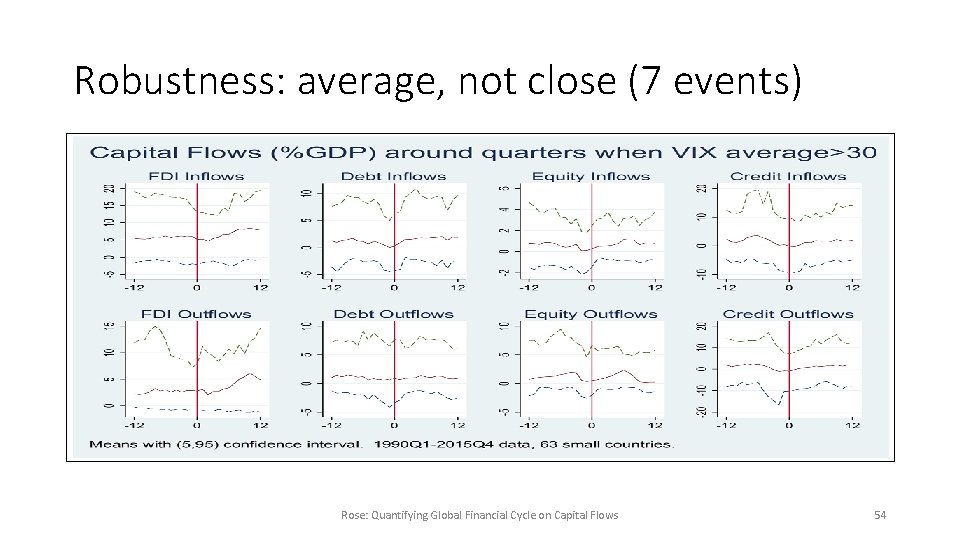
Robustness: average, not close (7 events) Rose: Quantifying Global Financial Cycle on Capital Flows 54

Extensions • Out of sample techniques? • Non-linearities? • Adding intrinsic dynamics (long-run/short-run differences)? • Mostly: Improving capital flow equations by adding domestic demand/supply factors • Any domestic/GFCy correlation likely to reduce impact of latter • Includes endogenous domestic policy responses • These omissions a likely reason for poor fit of regressions Rose: Quantifying Global Financial Cycle on Capital Flows 55
- Slides: 55