How Errors Propagate Error in a Series Errors

How Errors Propagate • Error in a Series • Errors in a Sum • Error in Redundant Measurement

Error in a Series • Describes the error of multiple measurements with identical standard deviations, such as measuring a 1000’ line with using a 100’ chain. • Eseries En

• Esum is the square root of the sum of each of the individual measurements squared • It is used when there are several measurements with differing standard errors Esum E 1 E 2 E 3 . . . En 2 2

Error in Redundant Measurements • If a measurement is repeated multiple times, the accuracy increases, even if the measurements have the same value Ered. meas. E n

If you learn one thing… • With Errors of a Sum (or Series), each additional variable increases the total error of the network • With Errors of Redundant Measurement, each redundant measurement decreases the error of the network. • As the network becomes more complicated, accuracy can be maintained by increasing the number of redundant measurements

Introduction to Adjustments • Adjustment - “A process designed to remove inconsistencies in measured or computed quantities by applying derived corrections to compensate for random, or accidental errors, such errors not being subject to systematic corrections”.

Introduction to Adjustments • Common Adjustment methods: Compass Rule Transit Rule Crandall's Rule Rotation and Scale (Grant Line Adjustment) Least Squares Adjustment

Weighted Adjustments • Weight - “The relative reliability (or worth) of a quantity as compared with other values of the same quantity. ”

Weighted Adjustments • The concept of weighting measurements to account for different error sources, etc. is fundamental to a least squares adjustment. • Weighting can be based on error sources, if the error of each measurement is different, or the quantity of readings that make up a reading, if the error sources are equal.

Weighted Adjustments • Formulas: • W (1 E 2) (Error Sources) • C (1 W) (Correction) • W n (repeated measurements of the same value) • W (1 n) (a series of • measurements)

Weighted Adjustments • Example A = 43 24’ 36”, 2 x A B = 47 12’ 34”, 4 x C = 89 22’ 20”, 8 x Perform a weighted adjustment based on the above data C B

ea No . M E GL AN s Example Mean Value Rel. Corrections Adjusted Value A 2 43 24’ 36” 4/ 7 X 30” = 17” 43 24’ 53” B 4 47 12’ 34” 2/ 7 X 30” = 09” 47 12’ 43” 1/ 7 X 30” = 04” 89 22’ 24” = 30” 180 00’ 00” The relative correction for the three angles are 1 : 2 : 4, the inverse proportion to the number of turned angles. This is the first set of relative corrections. The sum of the relative corrections is 1 + 2 + 4 = 7 , This is used as the denominator for the second set of corrections. The sum of the second set of relative corrections shall always equal 1. The second set is used for corrections. C 8 89 22’ 20” 1/ 7 TOTALS 179 59’ 30” 7/ 7

Introduction to Least Squares Adjustment • A rigorous statistical adjustment of survey data based on the laws of probability and statistics • Provides simultaneous adjustment of all measurements • Measurements can be individually weighted to account for different error sources and values • Minimal adjustment of field measurements

Least Squares Adjustment • A Least Squares adjustment distributes random errors according to the principle that the Most Probable Solution is the one that minimizes the sums of the squares of the residuals. • This method works to keep the amount of adjustment to the observations and, ultimately the ‘movement’ of the coordinates to a minimum.

Least Squares • The Iterative Process • • • Creates a calculated observation for each field observation by inversing between approximate coordinates. Calculates a "best fit" solution of observations and compares them to field observations to compute residuals. Updates approximate coordinate values. Calculates the amount of movement between the coordinate positions prior to iteration and after iteration. Repeats steps 1 - 4 until coordinate movement is no greater than selected threshold.

Least Squares • Four component that need to be addressed prior to performing least squares adjustment 1. 2. 3. 4. Errors Coordinates Observations Weights

Each Observation Requires an Associated Weight • Weight = Influence of the Observation on Final Solution • Larger Weight - Larger Influence • Weight = 1/σ2 • σ = Standard Deviation of the Observation • The Smaller the Standard Deviation the Greater the Weight

Weighting Methods • Observational Group • Least Desired • Angles weighted at accuracy of total station • Individually weighted • Best • Std dev. Of field observation used as weight

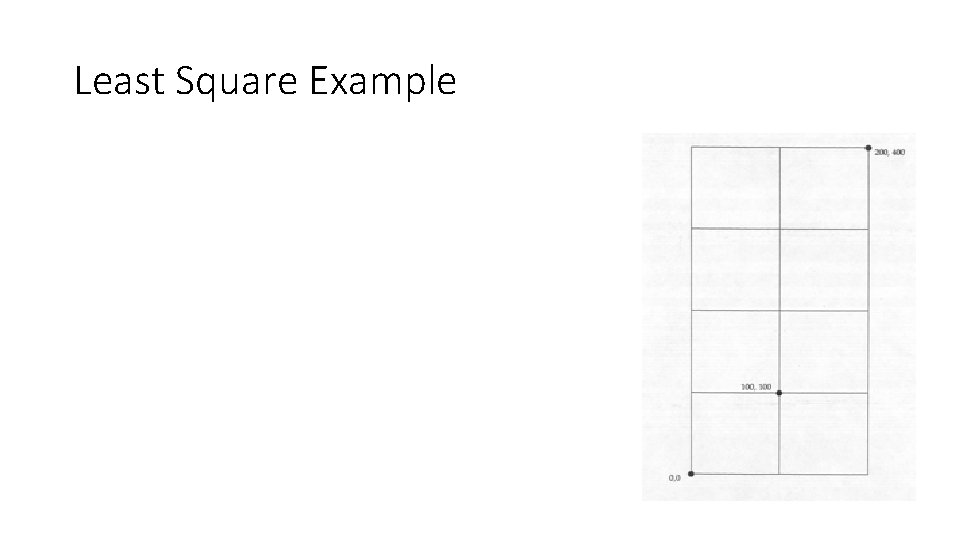
Least Square Example

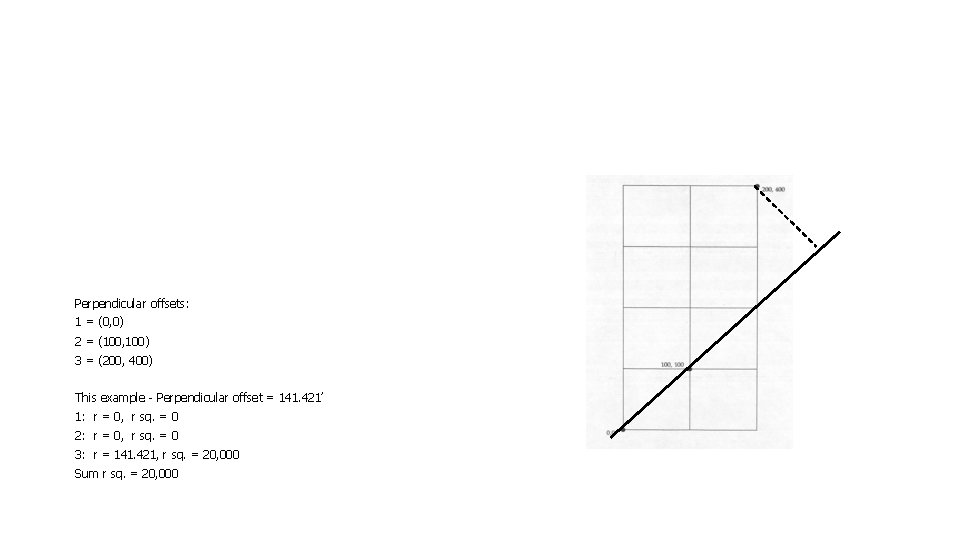
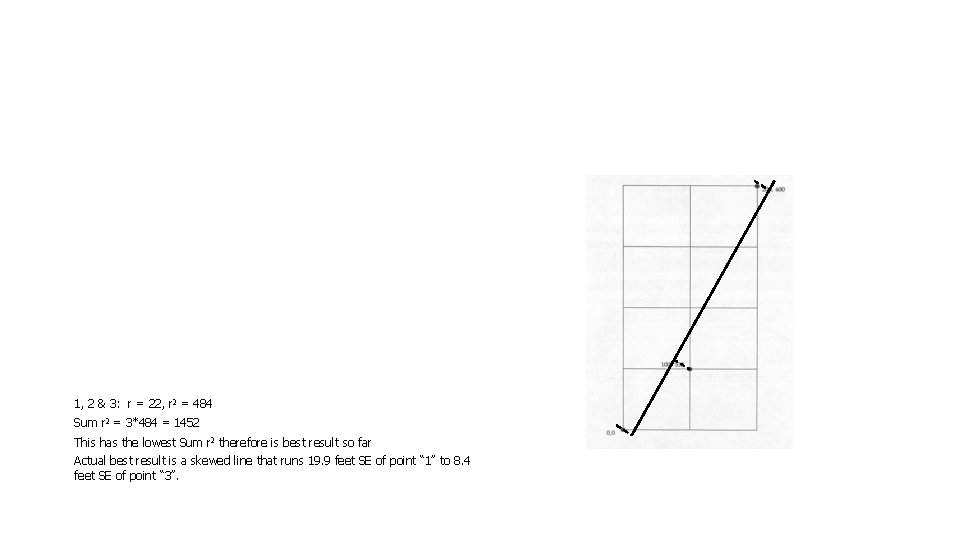
Perpendicular offsets: 1 = (0, 0) 2 = (100, 100) 3 = (200, 400) This example - Perpendicular offset = 141. 421’ 1: r = 0, r sq. = 0 2: r = 0, r sq. = 0 3: r = 141. 421, r sq. = 20, 000 Sum r sq. = 20, 000

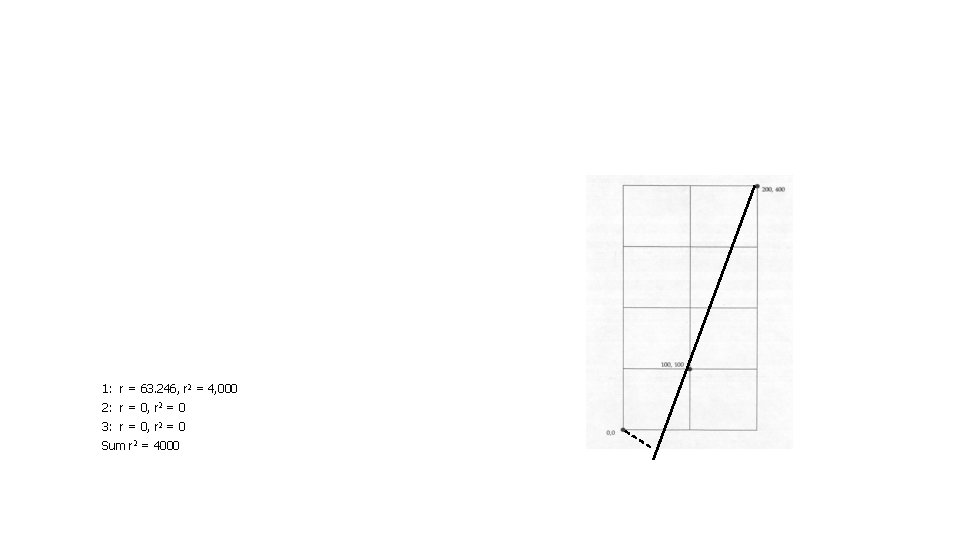
1: r = 63. 246, r 2 = 4, 000 2: r = 0, r 2 = 0 3: r = 0, r 2 = 0 Sum r 2 = 4000

1, 2 & 3: r = 22, r 2 = 484 Sum r 2 = 3*484 = 1452 This has the lowest Sum r 2 therefore is best result so far Actual best result is a skewed line that runs 19. 9 feet SE of point “ 1” to 8. 4 feet SE of point “ 3”.