How Does Spare Capacity and Topology Affect the

How Does Spare Capacity and Topology Affect the Security of Resource Networks? Qian-Chuan Zhao zhaoqc@tsinghua. edu. cn Qing-Shan Jia jiaqs@tsinghua. edu. cn Yang Cao caoy 02@mails. tsinghua. edu. cn

Outline n How much spare capacity is necessary? n n Models: Balanced partition & node-weighted graph The necessary condition on spare capacity Critical value of the linearly increasing speed How topology affects security: An upper bound of resource network security n n n Motivation Upper bounds of security Identification of critical transmission lines 2

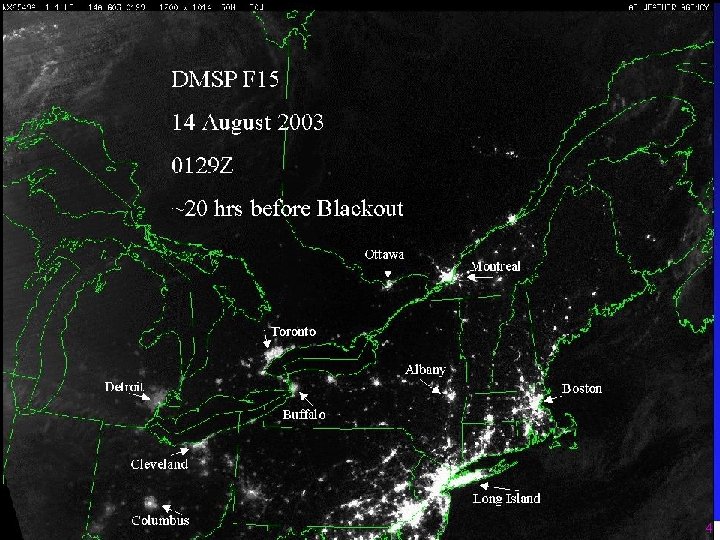
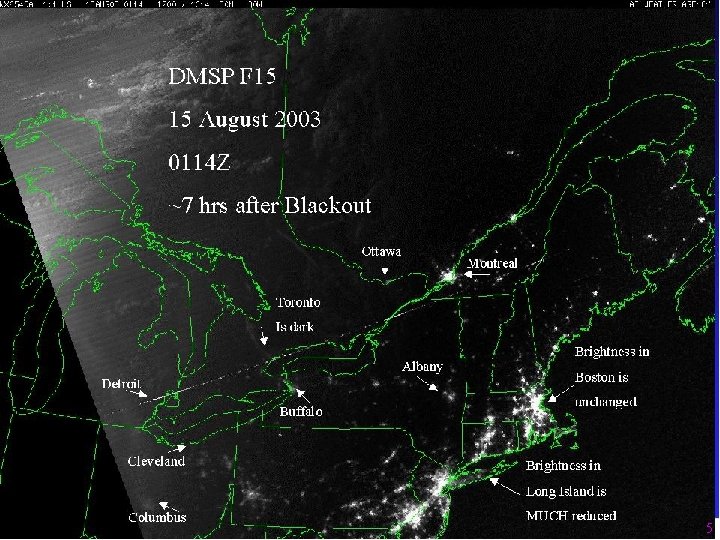
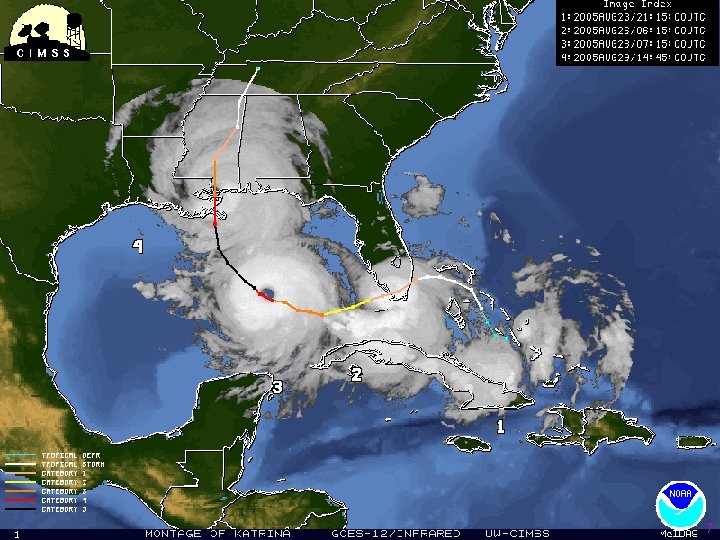
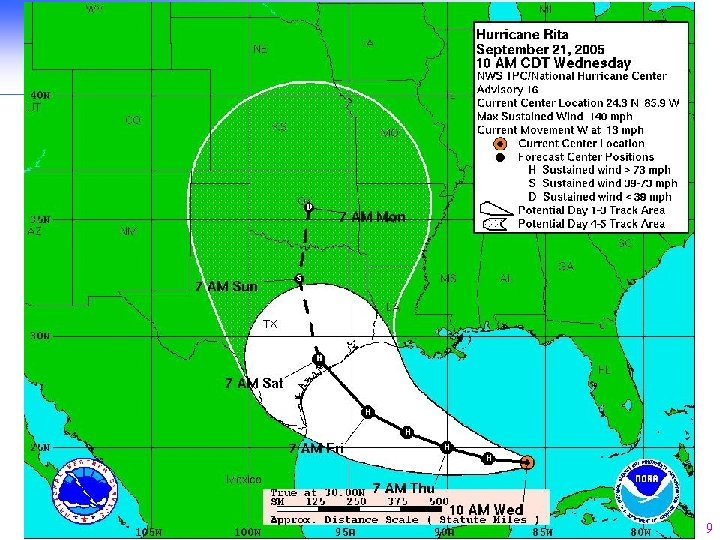
Motivation n Real life examples: n n Aug. 14, 2003 blackout of the North American electric power network in USA and Canada [Canada. USPSOTF 2004] Summer of 2005, Hurricanes Katrina & Rita, record prices in the US oil market Jan. 2006, gas pricing dispute between Russia & Ukraine, shortage in Ukraine and throughout western Europe … 3

4

5

6

7

Hurricane Rita 8

9

10

Gas Pricing Dispute 11

Motivation n n Necessary condition: balance between generation & consumption Why do local contingencies lead to global performance degradation? Practical solution: Spare capacity (e. g. , backup generators, load shedding), costly, growing network capacity Interesting question: How much spare capacity is necessary for the security of resource network? 12

Related work in Physics n n n Network structure + node/edge dynamics network complexity Network resilience w. r. t. remove of nodes or edges Results n n Many real life networks & artificial network, robust to random failure, fragile to intentional attacks Critical components cascading failure 13

Difference in the model Our model Previous models Critical condition: balance Contingency Separation contingency Remove of nodes/edges Measure of security BP probability connectivity 14

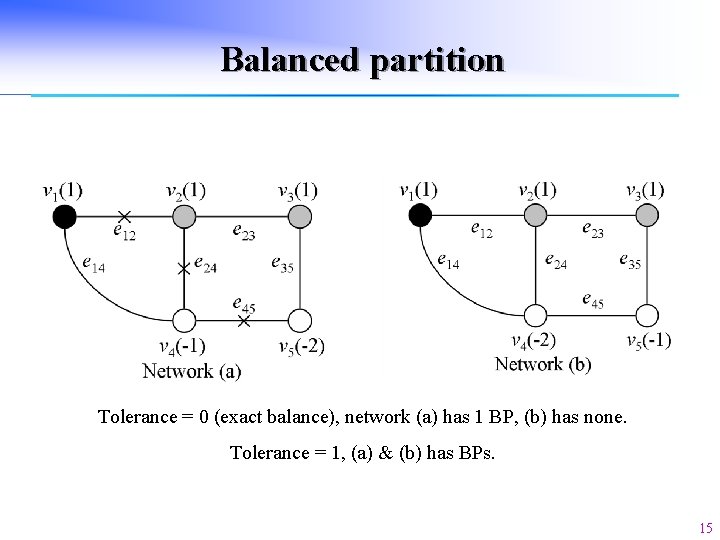
Balanced partition Tolerance = 0 (exact balance), network (a) has 1 BP, (b) has none. Tolerance = 1, (a) & (b) has BPs. 15

The question n n Fix the topology Given the separation contingency, network capacity (i. e. , total power consumption) & tolerance (i. e. , spare capacity) Consider all generation patterns and load patterns Measure the BP probability When the network capacity , how fast to increase the tolerance s. t. the BP prob. >0? 16

Experiment I: Complete Graph 17

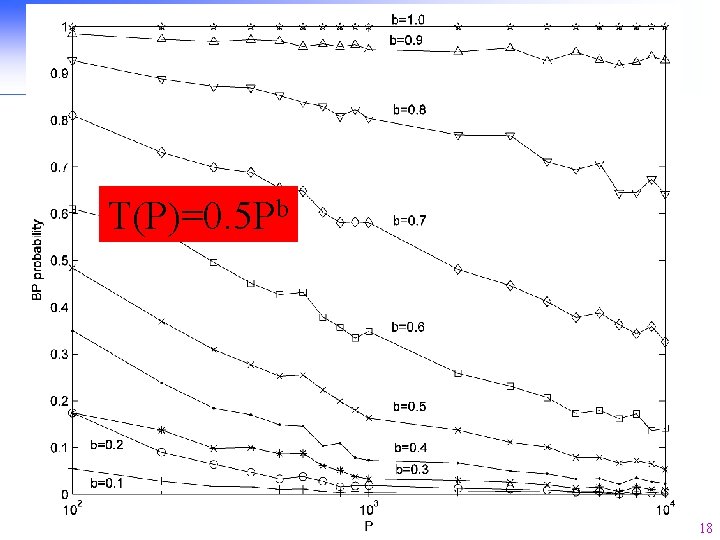
Experiment I: Result T(P)=0. 5 Pb 18

Theoretical Result I n n Theorem 1: When the tolerance increases slower than a linear function of the growing network capacity, then the BP probability will converge to zero. Proof (see [Zhao. Jia. Cao 2007]) 19

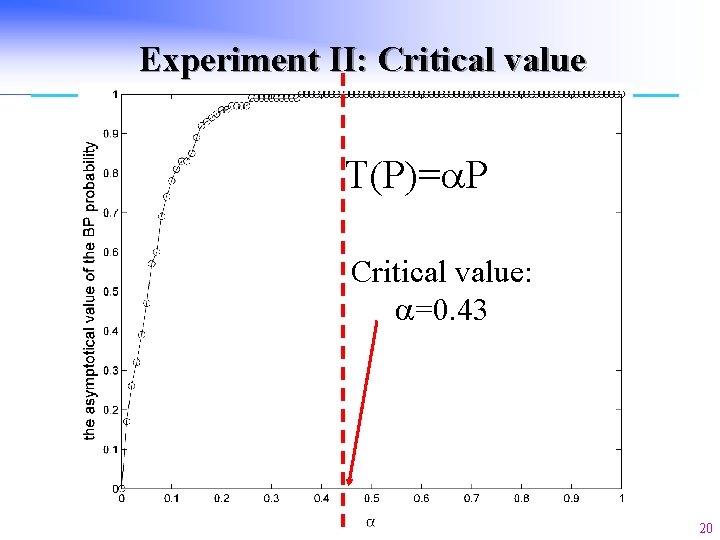
Experiment II: Critical value T(P)=a. P Critical value: a=0. 43 20

Theoretical Result II n n There is a critical value of the linearly increasing speed of the tolerance ac. If a<ac, BP prob. Still decreases to zero when the network capacity . Proof (See [Zhao. Jia. Cao 2007]). 21

Partial Conclusion n How much spare capacity is necessary for the security of resource networks? At least linearly increase the spare capacity when the network capacity increases. The linear increasing speed should be no less than a critical value. 22

How Topology Affects the Security

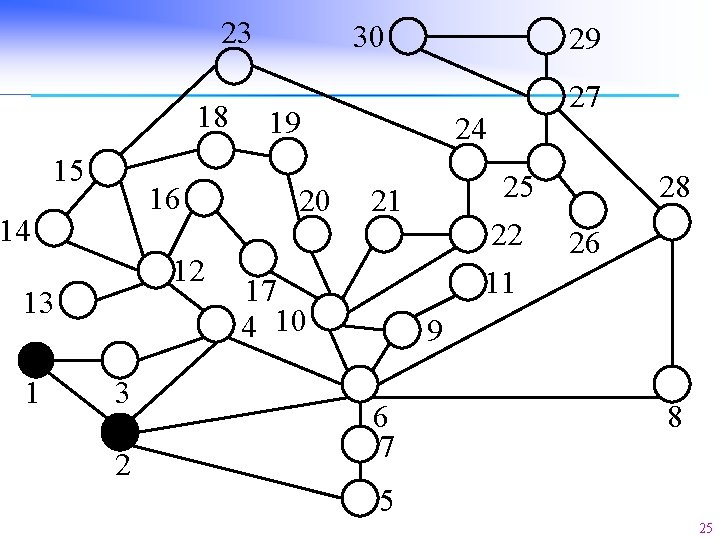
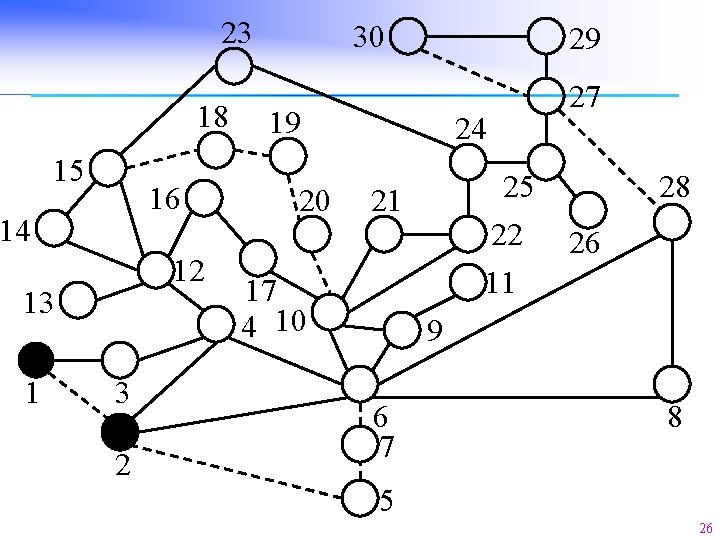
Motivation n n Fixing the topology, considering single and multiple line outages, what’s the probability for a power network to collapse (i. e. , large load shedding)? Formulate a decision problem: will a line outage contingency cause a collapse (i. e. , a large load shedding)? Use Ordered Binary Decision Diagram (OBDD) to count the line outages leading to collapse. The sum of the probabilities of these line outages gives a lower bound of collapse probability, i. e. , an upper bound of security. By counting the appearance of each line in the fatal line outages, we identify the critical lines. 24

23 18 15 16 14 12 13 1 3 2 30 29 19 20 24 25 22 11 21 17 4 10 27 28 26 9 6 7 8 5 25

23 18 15 16 14 12 13 1 3 2 30 29 19 20 24 25 22 11 21 17 4 10 27 28 26 9 6 7 8 5 26

Conclusions n n Necessary condition of security: resource balance condition. How much spare capacity is necessary for the security of resource networks? n n Linear increasing, with rate greater than a critical value. How topology affects security: an upper bound of security. n n OBDD-based fast enumeration. Identifies critical transmission lines. 27

Thank you! Q&A 28