How do weights affects approximation algorithms How do

How do weights affects approximation algorithms?

How do weights affects approximation algorithms? As usual there are no rules whatsoever.

No suspense: no rules on when weights make a difference � However I will provide some interesting examples in which weights make a difference � I will try and say for every problem, why weights make a difference. � But without deep insight � One clear thing: I will speak only on stronly NP hard problem. Otherwise weights make a huge difference for the Knapsack problem.

Any general rules? � Well, lets show a trivial one � Say it’s a maximization problem � Say that if A is a feasible solution then so is any B A � In such case clearly the difference between the weighted and unweighted case is limited � Bucketing shows that the difference in the ratio is at most O(log n).

Also say we use just mathematical programming � The weights should not matter � Also consider a problem like the Directed Steiner tree/forest/network � A typical removal of weights? Change an edge to a path. � When does this not work? � If the ratios are polynomial like n 1/2 � In such a case this changes n and this can not be used. � But it works for polylog ratios.

Knapsack Set-Coverage � The Set-Coverage problem is given a set system and a number k select k sets that cover as many elemnts as possible. � Knapsack version, not that known: � Each set has cost c(s) and there is a bound B on the maximum sum of costs, of sets we can choose. � Maximize number of elements covered.

Result due to Khuller , Moss and, Naor, 1997, IPL � The (1 -1/e) ratio is possible. the usual algorithm & analysis (1 -1/e) only follows if we can add the last set in the greedy choice. Thus, fails. � Because most times, adding the last set will give cost larger than B. � Trick: guess the 3 sets in OPT of least cost. Then apply greedy (don’t go over budget B). � Then a ratio of (1 -1/e) follows. � In

A remark: � Since then, many problems like that were studied � An optimal (1 -1/e) ratio by Vondrak: Maximizing a submodular problem under Matroid contraint. � Solved a 30(!) years old problem. � Many problems were studied under Knapsack constrains way more general than Max Coverage. � A cute remark: guessing 2 elements gives ratio ½. Guessing one element: unbounded ratio.

Augmenting edge connectivity from 1 to 2 Given: undirected graph G(V, E) And a set of extra legal for addition edges F called “links” Required: a subset F’ F of minimum size so that G(V, E+F’) is 2 -edge-connected

Bi-Connected Components G A H F B C D E

The tree augmentation problem Input: A tree T(V, E) and a separate set F of edges called “links” Output: Add minimum amount of links F’ from F so there will be no bridges (G+F’ is 2 EC)

So far weights matter � K, Nutov TALG 2016: a 3/2 approximation algorithm for the case links have cost 1. � Giving a 1. 8 ratio is easier (albeit complex still) � The version with weights: add a set of links F of minimum cost so that G+F is 2 -connected. � Not known better than 2 (many algorithms give ratio 2)

A recent breakthrough David Adjiashvili. A recent paper. Gives 1. 946 ratio for weighted TAP but if the largest edge weight is bounded by a constant. I went through 3 stages with respect to this Algorithm. Let me give a similar case from cinema.

In 1968 a new extremely strange film came out. The film was called “ 2001: A Space Odyssey” Woody Allen on the film: 1) I went to see the movie and I really did not like it. 2) But I was not sure and I went again and liked it more. 3) Then a friend of mine told me there is a great film 2001: A Space Odyssey.

I went with the friend to see it for the third time. And I said to myself: this is simply wonderful stuff!! And Allen that is not modest said: This was one of the only times in which the director was way ahead of me. Note that he is more or less saying that except the director above he is one of the smartest.

The three phases of Woody Allen At the start I was sure it is a mistake (namely I did not really like it, like Woody Allen). It did not help that I did not understand anything. But then I read it a second time and I found some nice ideas. Then me and Zeev, decided to take 7 days to read it. We talked on the phone and agreed: this is (correct and) has some wonderful stuff! Still the question if there is better than ratio 2 for the problem with costs, is open.

What is the diffficulty? � We discussed leaf closed trees. � These are subtrees so that all the links that touch the leaves stay inside the subtree. � We cover at each stage a generalization of this notion. � Now say that there are costs. � The notion of leaf closed trees becomes meaningless.

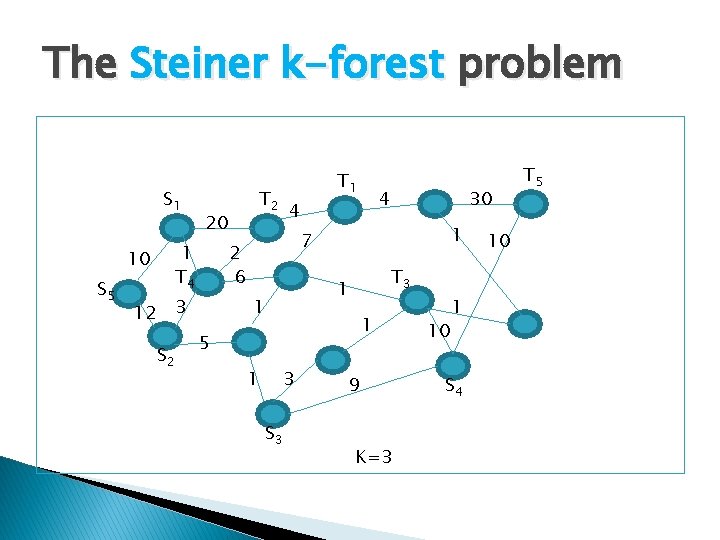
The Steiner k-forest problem S 1 S 5 20 1 T 4 10 S 2 4 4 30 1 7 2 6 3 12 T 1 T 3 1 1 1 5 1 3 S 3 9 K=3 10 1 S 4 10 T 5

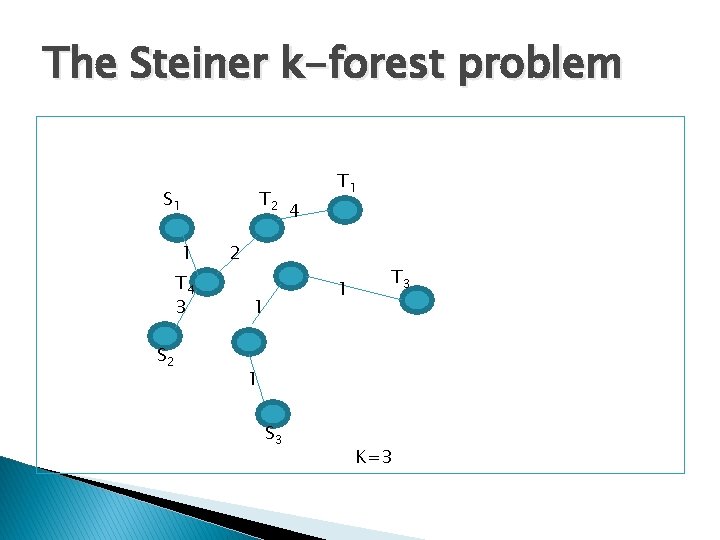
The Steiner k-forest problem S 1 T 2 1 T 4 3 S 2 T 1 4 2 1 1 T 3 1 S 3 K=3

The capacitated non Preemptive Dial a Ride Problem � We are given a graph and input of m pairs {s I , t I } and a car with capacity k. A client is located at s I and needs to be taken to t I. � Once you take a passenger at s I she only leaves the car when the car reaches t I � Note that a Steiner k-forest can be turned into a path of no larger cost. The problems are closely related. � Both Dense k-Subgraph hard.

What is known for the problems � SKF: ratio min{O(sqrt k), O(sqrt n)} by Gupta, Hajiaghayi, Nagarajan and Ravi. � Dense k-Subraph hard probably means no better than poly ratio. � Same goes for Dial-a-Ride.

Better ratio for almost uniform weights that the weights are between 1 and n for small enough � Say � Then the Steiner k-Forest problem admits a n 0. 449 approximation ratio. Dinitz , K, Nutov. � Dial a ride admits an O(sqrt{n}) ratio by Charikar, Raghavachari. � Almost uniform weights we get n 0. 449 to the Dial a ride problem.

Why cant we handle the weighted case � We get a graph with “few vertices” and this implies that a tree on this graph has “few edges”. This does not work for the weighted case. � We identified a problem that if has a good approximation we can break the ratio for the weighted case. � But this problem seems very hard to approximate.

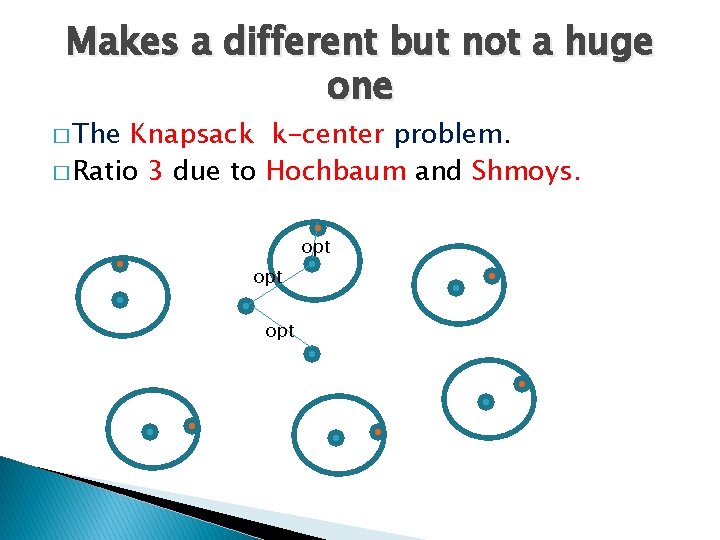
Makes a different but not a huge one � The Knapsack k-center problem. � Ratio 3 due to Hochbaum and Shmoys. opt opt

A paper by Chuzhoy et al � To give credit where its due two groups one of 3 (Halperin, Krauthgamer, K) and another group of 4 by Chuzhy et al, got the same results by the same techniques. � We had to join � We turned out from the three musketeers to the seven dwarfs - � The main result was a lower bound of log *n for the directed k-center problem. � This is a tight ratio!

Another result � It turns out that the Knapsack k-center problem admits no 3 - ratio unless P=Quasi(P). 18 years open question. � Thus the weights made a difference in the constant. � In center problem we are used to ratio 2. � Say that there is a collection of vertices that can be centers and those who are clients. � Distance 1 for every vertex in a yes instance and otherwise the distance is 3.

A difference of log n � The Vertex Cover problem with hard capacity bounds � Every vertex has a hard bound b(v) on the number of edges that it can cover. � After selecting the VC assign edges to vertices so that v gets not more than b(v) edges � Checking feasibility can be done by flow. � Interestingly Its enough to give a fractional assignment since it implies an integral one.

Example 2 4 3 3 5 3 3

A log n hardness for the weighted case � 1 3 0 1 3 1 2 2 2

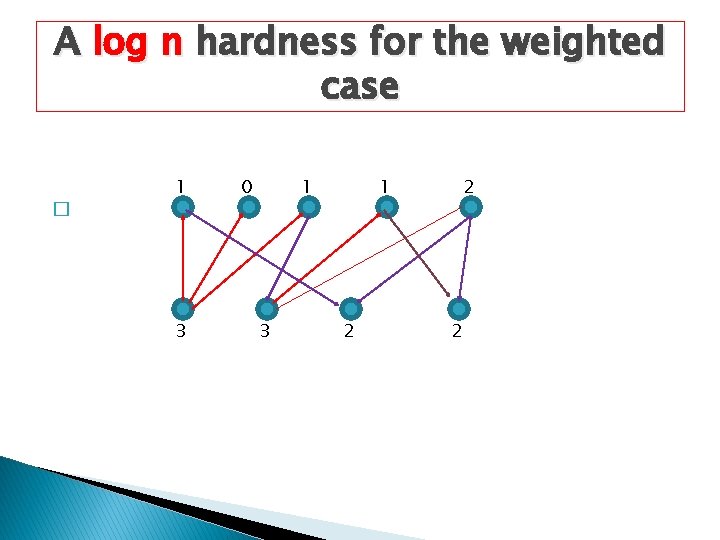
A log n hardness for the weighted case � 1 3 0 1 3 1 2 2 2

Why does not work for the weighted case � Chuzhoy and Naor (gave ratio 3) used a charging scheme that works till the last element is charged, If its weighted, the charge is too much. If uniform cost, charged 1. � Our improvement (Halperin et al) runs into the same difficulty. We gave improve ratio 2 � Hugely complex paper. � Thus a slightly larger difference: log n versus 2.

Another example of log n gap � Connected Vertex Cover. � Khuller: take a DFS and the tree but the leaves. Gives ratio 2 for costs 1 (there is always a matching of size n-L). � Not published anywhere but if vertices have weights the problem becomes at least as hard as Set Cover � Which means that a ratio better than O(log n) is not possible. See a recent (1 - )*ln n lower bound under P NP by Dinur et al.

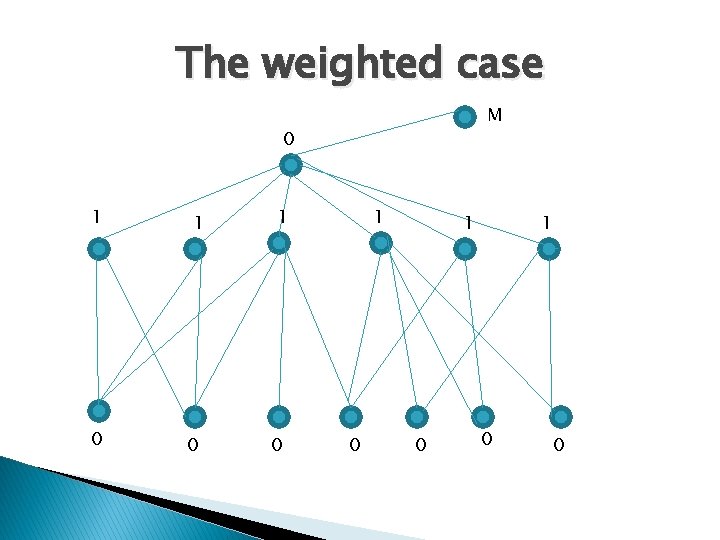
The weighted case M 0 1 0 1 0 1 0 0

All zero cost vertices are taken M 0 1 0 1 0 1 0 0

But this does not give connectivity M 0 1 0 1 0 1 0 0

Need to add edges to a Set Cover M 0 1 0 1 0 1 0 0

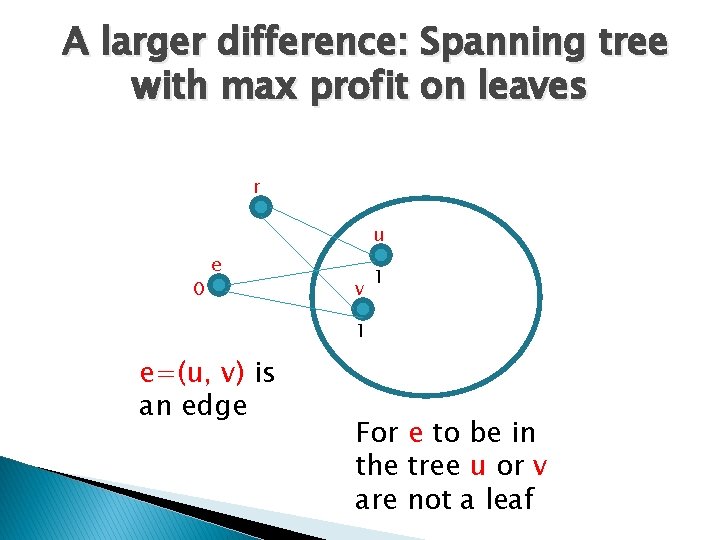
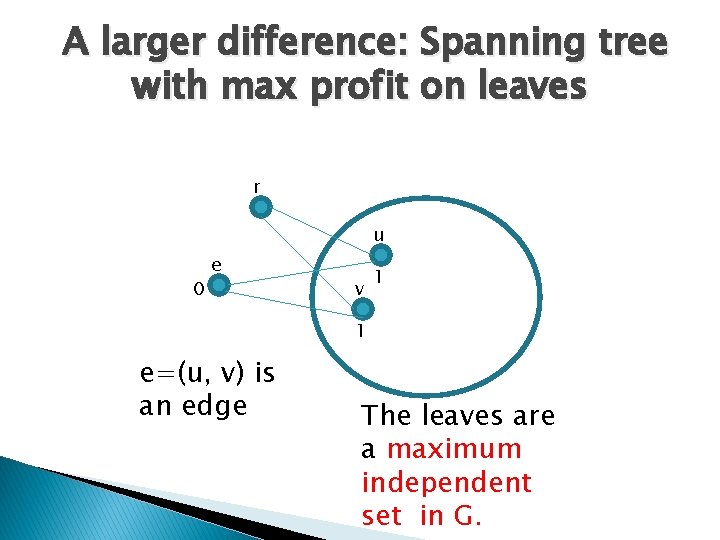
A larger difference: Spanning tree with max profit on leaves r u 0 e v 1 1 e=(u, v) is an edge For e to be in the tree u or v are not a leaf

A larger difference: Spanning tree with max profit on leaves r u 0 e v 1 1 e=(u, v) is an edge The leaves are a maximum independent set in G.

Thus the weighted case spanning tree is hard. � The Independence Set problem admits no n 1 - approximation for any constant >0. However say that the costs are uniform. Say that we look for the tree with most leaf but does not need to be spanning. Add a neighbor to any leaf. The number of leaves does not change. Thus we may assume its spanning w. l. o. g

The ST with maximum num of leaves �Solis-Oba gave a ratio 2 for the problem. �One of the largest differences I could find: �Weighted: n 1 - hardness �Unweighted ratio 2! �What is the problem with the spanning tree when there are weights? �The fact that its spanning means that all vertices have to be in. �This makes profitable vertices unable to be leaves.

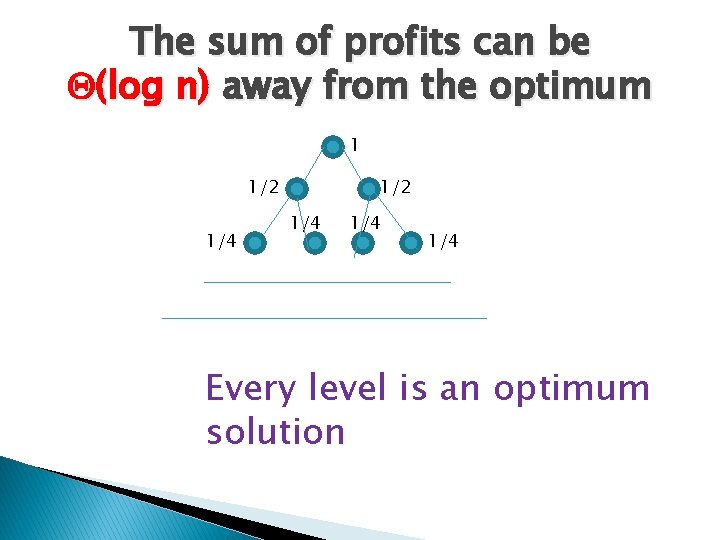
A related problem � Say that the vertices have profits and we want a not necessarily spanning tree with max profit on the leaves. Also we deal with the directed case. � Hajiaghayi, K, R. Gandi, Purohit, and Sarpatwar. � We do not know if weights make a difference. � We give constant ratio for weights 0, 1. � Bucketing gives ((log n) ratio for the weighted case. � I will present a tree that may mean that the weighted case may be harder.

The sum of profits can be (log n) away from the optimum 1 1/2 1/4 1/4 Every level is an optimum solution

Why do weights make a difference? � The problem of finding a tree with maximum number of leaves has ratio 2. � This can be used to approximate the case of weights 1, 0. � But it does not seem to be able to be used to approximate the case of vertex profits. � Thus using the 0 profit we can use bucketing.

The Connected Max Cut problem � Given a graph G(V, E) choose a set S so that G(S) is connected and the size of the cut e(S, V-S) is maximum. � Hajiaghayi, K, Mackdavid, Purohit, and Sarpatwar. �A reduction from the weighted problem to the weighted problem by putting profits deg(v) on vertices of the max leaf problem. This improves the ESA paper ratio to O(log n) for CMC. � We do not know if the difference is inherent.

Spanners �Input: An undirected graph G(V, E) and an integer k �Objective: find a subgraph G’ so that for every u and v: Dist (u, v)/Dist (u, v)≤ k G’ G Invented by Peleg and Ullman

Approximation 2 -spanners � If length 1 and costs are arbitrary the problem admits an O(log n) approximation. 1992, K, Peleg � In 1998: K: unless P=NP log n is optimal. Remark: even with costs and lengths 1, the 3 spanner problem is Labelcover hard. � Dinitz, K, Raz ICALP 2012. Solves an Open problem poses in 1992 by K, Peleg. �

The algorithm: For a vertex v look at the graph induced by N(v) � Find a densest subgraph S(v) in N(v) � Return the edges from v to S(v) that is the most dense set over all v and iterate. � Using “few” edges to “cover” many edges. S

What happens if general lengths? � The 2 -spanner problem becomes Labelcover hard. Elkin Peleg. � When there arbitrary lengths an edge can be replaced by a path of any length. And thus the problem becomes very complex. Difference: uniform (log n). � Labelcover-hard problems probably have only polynomial ratios.

Having fun with connectivity problems � Min size k-connected subgraph ratio 1+2/k � The metric case 2+1/(k-1) K, Nutov. � Improving Khuller et al. 2+2/(k-1). More importantly, the first but same ratio for the directed case. � General �I weights O((log n)2) Nutov. had the best ratio with Nutov but was improved twice. � A general request: work on other people problems.

Technique 2: The Cycle Theorem of Mader Let G(V, E) be a k-vertex connected graph, minimal for edge deletion and let C be a cycle in G Then there is a vertex in C of degree exactly k Strange Claim?

Corolloraly Say that (G) is at least k-1 Let F be any edge minimal augmentation of G to a kvertex-connected subgraph Then F is a forest

Proof Consider a cycle in F As all degrees are at least k-1 before F, with F all degrees are at least k+1 which contradicts Mader’s theorem.

A simple algorithm � Cheriyan & Thurimella : 1+2/k � Find a graph G(X) with minimum number of edges so that all degrees are at least k-1. � Clearly this requires opt. � Add a minimal extension solution. � By Mader Theorem we added n-1 edges. � Note that opt≥k∙n/2

Approximation ratio � Opt+ � This n-1/opt≤ opt+2(n-1) /(n ∙k) implies 1+2/k ratio. � The ratio 2+ (k-1)/n, K. Nutov for metric weights, complex. � The O((log n)2) of Nutov for general weights very complex. � Disclamer: no lower bounds!

Preservers � The input contains a collection of pairs {x, y} and you want minimum edges G’ so that the distance between every x, y is the same as in G. Our paper only for uniform length. � The paper by Chlamtac, Dinitz, K, Laekhanukit, SODA 2017. � Ratio O(n 3/5 ) approximation for preservers. � The big problem was that there was no Ω(n) � Lower bound

Using junction trees T 1 T 2 Tk S 1 S 2 Sk

Another way to bound the cost �The number of pairs times the maximum length of a path �Note that if the edges have non uniform weights there would not be paths of the same cost. �We do not have a ratio for the weighted case. �But we have a O(n 3/5 ) ratio for uniform weights.

Other open problems? � See several similar open questions in our SODA 2017 paper. � Define a large enough collection of problems and some properties that will assure that weights do not matter/do matter. � A rather hard task. � The nicest open question: Give a ratio better than 2 for the Tree Augmentation problem. � From all problems I have shown, this is my favorite.