How do Radio Telescopes work K Y Lo

How do Radio Telescopes work? K. Y. Lo National Radio Astronomy Observatory September 2005 – Indiana Universe

Electromagnetic Radiation Wavelength Radio Detection techniques developed from meter-wave to submillimeter-wave: = 1 meter = 300 MHz = 1 mm = 300 GHz National Radio Astronomy Observatory September 2005 – Indiana Universe

General Antenna Types Wavelength > 1 m (approx) Wire Antennas Dipole Yagi Helix or arrays of these Wavelength < 1 m (approx) Reflector antennas Feed Wavelength = 1 m (approx) Hybrid antennas (wire reflectors or feeds)

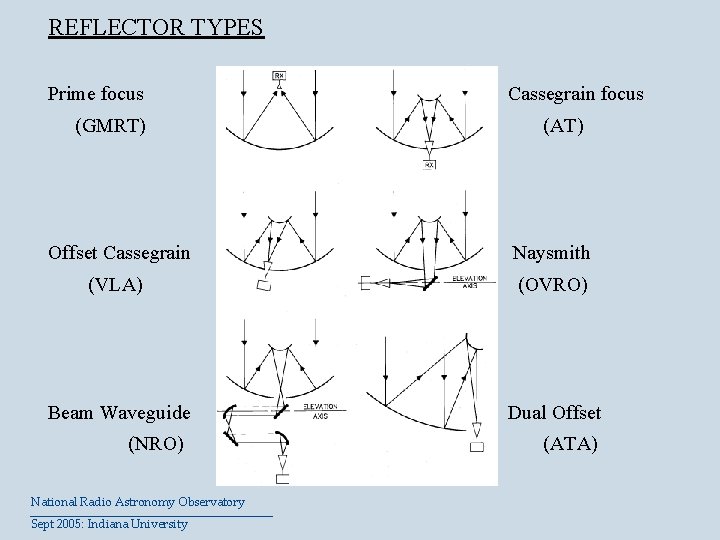
REFLECTOR TYPES Prime focus Cassegrain focus (GMRT) (AT) Offset Cassegrain Naysmith (VLA) Beam Waveguide (NRO) National Radio Astronomy Observatory Sept 2005: Indiana University (OVRO) Dual Offset (ATA)

REFLECTOR TYPES Prime focus (GMRT) Cassegrain focus (AT) Offset Cassegrain Naysmith (VLA) (OVRO) Beam Waveguide Dual Offset (NRO) National Radio Astronomy Observatory Sept 2005: Indiana University (ATA)

What do Radio Astronomers measure? • Luminosity of a source: L = d. E/dt erg/s • Flux of a source at distance R: S = L/4 R 2 erg/s/cm 2 • Flux measures how bright a star is. In optical astronomy, this is measured in magnitudes, a logarithmic measure of flux. National Radio Astronomy Observatory Sept 2005: Indiana University • Intensity: If a source is extended, its surface brightness varies across its extent. The surface brightness is the intensity, the amount of flux that originates from unit solid angle of the source: I = d. S/d erg/s/cm 2/steradian

Measures of Radiation • The following should be clear: L = S d = 4 R 2 S for isotropic source 4 S = I d source • Since astronomical sources emit a wide spectrum of radiation, L, S and I are all functions of or , and we need to be more precise and define: • Luminosity density: L( ) = d. L/d W/Hz • Flux density: S( ) = d. S/d W/m 2/Hz • Specific intensity: I( ) = d. I/d W/m 2/str/Hz • The specific intensity is the fundamental quantity characterizing radiation. It is a function of frequency, direction, s, and time. • In general, the energy crossing a unit area oriented at an angle to s, specified by the vector da, is given by d. E = I( , s, t) s da d d dt = I ( , ) s da d d dt

Analogs in optical astronomy • Luminosity is given by absolute magnitude • Flux, or brightness, is given by magnitudes within defined bands: U, B, V • Intensity, or surface brightness, is given by magnitude per square arc-second • Optical measures are logarithmic because the eye is roughly logarithmic in its perception of brightness • Quantitatively, a picture is really an intensity distribution map National Radio Astronomy Observatory Sept 2005: Indiana University

Rayleigh-Jeans Law and Brightness Temperature • The Specific Intensity of thermal radiation from a black-body at temperature T is given by the Planck Distribution: I = (2 h 3/c 2)/[exp(h /k. T) 1] = (2 hc 3/ 2)/[exp(hc/ k. T) 1] = 2 k. T/ 2 if >> hc/k. T or h << k. T, R-J Law • Brightness Temperature Tb ( 2/2 k) I = T for thermal radiation • Brightness temperature of the Earth at 100 MHz ~ 108 K (due to TV stations) National Radio Astronomy Observatory Sept 2005: Indiana University

Antenna = Radio Telescope • The function of the antenna is to collect radio waves, and each antenna presents a cross section, or Effective Area, Ae( , ), which depends on direction ( , ) • The power collected per unit frequency by the antenna from within a solid angle d about the direction ( , ) is given by d. P = ½ I ( , ) Ae ( , ) d W/Hz The ½ is because the typical radio receiver detects only one polarization of the radiation which we assume to be unpolarized. National Radio Astronomy Observatory Sept 2005: Indiana University

• The power density collected by the antenna from all directions is P = ½ I ( , ) Ae ( , ) d W/Hz • Antenna Temperature TA is defined by TA = P /k in K (Nyquist Theorem) • Therefore TA = (1/2 k) I ( , ) Ae ( , ) d K • For a point source, I = S ( , ) k. TA = ½ Ae, max S W/Hz if Ae ( , ) has a maximum value Ae, max at ( , ) = (0, 0) • (Maximum) Effective Area of an antenna: Ae, max = ap Ag m 2 where Ag is the geometric area and ap is the aperture efficiency. But, for a dipole antenna, Ag is zero but Ae is not. National Radio Astronomy Observatory Sept 2005: Indiana University

• Antenna pattern: Pn( , ) = Ae( , )/Ae, max Pn(0, 0) = 1 if the pattern is maximum in the forward direction • If the antenna is pointed at direction ( o, o) TA ( o, o) = (1/2 k) I ( , ) Ae ( o, o) d In terms of Tb and Pn , TA ( o, o) = (Ae, max/ 2) Tb ( , ) Pn ( o, o) d = (1/ A) Tb ( , ) Pn ( o, o) d where 2/Ae, max= A. Note the antenna temperature, which measures the power density P (W/Hz) collected by the antenna is the convolution of the antenna pattern Pn with the source brightness distribution Tb National Radio Astronomy Observatory Sept 2005: Indiana University

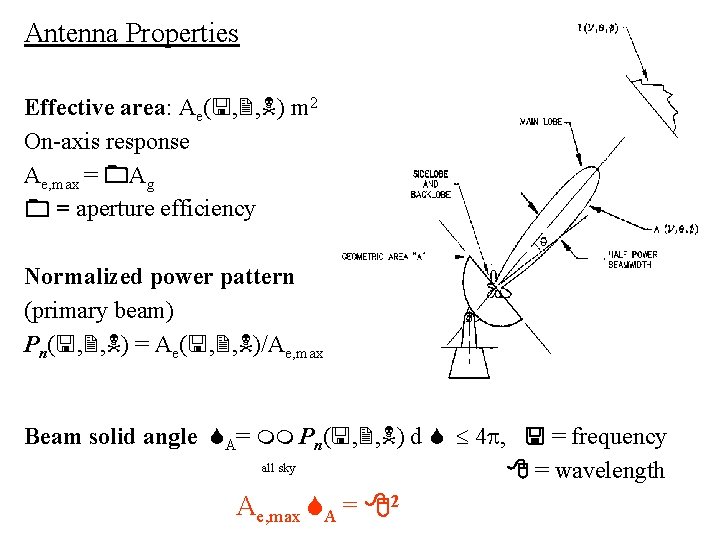
Antenna Properties Effective area: Ae( , , ) m 2 On-axis response Ae, max = Ag = aperture efficiency Normalized power pattern (primary beam) Pn( , , ) = Ae( , , )/Ae, max Beam solid angle A= Pn( , , ) d 4 , = frequency all sky = wavelength Ae, max A = 2

Mapping by an Antenna TA ( o, o) = (Ae, max/ 2) Tb ( , ) Pn ( o, o) d • Point source: Tb( , ) = ( 2/2 k)S ( , ) TA ( o, o) = (Ae, max/ 2) ( 2/2 k)S ( , ) Pn ( o, o) d = (Ae, max/2 k) S Pn ( o, o) Antenna pattern can be determined by scanning a point source If pointing at the point source, then k. TA = ½ Ae, max. S If S is known, then Ae, max can be determined by measuring TA • Unresolved source: s < m ~ A 2/Ae, max TA (0, 0) = (Ae, max/ 2) Tb ( , ) Pn ( , ) d = ( s/ A) Tb = ( m/ A) ( s/ m) Tb TA = m( s/ m) Tb Beam dilution National Radio Astronomy Observatory Sept 2005: Indiana University

Milky Way

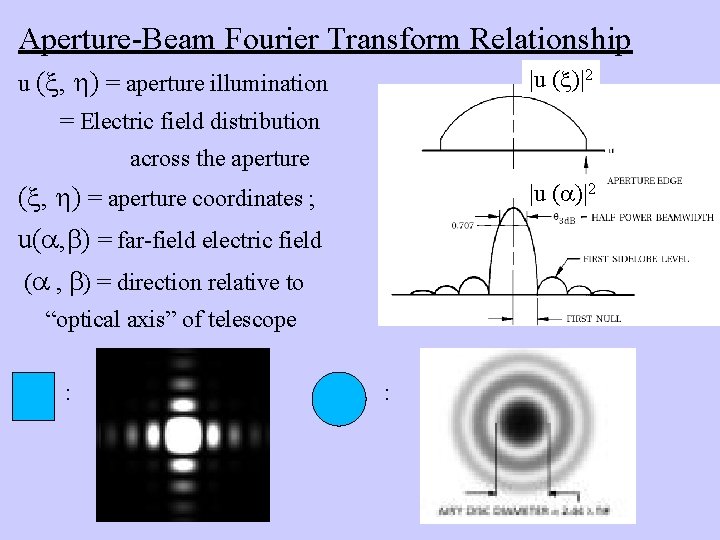
Maxwell Equations? • Radio telescopes operate in the physical optics regime, ~ D, instead of the geometric optics regime, << D, of optical telescope diffraction of radiation important • Easier to think of a radio telescope in terms of transmitting radiation • A point source of radiation (transmitter) at the focus of a paraboloid is designed to illuminate the aperture with a uniform electric field • The diffraction of the electric field across the aperture according to Huygens’ Principle determines the propagation of the electric field outward from the aperture or primary telescope surface • The transmitted electric field at a distant (far-field) point P in the direction ( , ) is given by the Fourier Transform of the electric field distribution across the aperture u( , ): u( , ) u( , ) exp[ 2 ( + )/ ] d d National Radio Astronomy Observatory Sept 2005: Indiana University

Antenna Pattern: Directional Response • Field Pattern of an antenna is defined by the Fourier Transform of the illumination of the aperture: u( , ) u( , ) • Antenna Pattern is defined in terms of power or the square of the E field, |u|2. Pn( , ) = |u( , )|2/|u(0, 0)|2 • Alternately, the antenna pattern is proportional to the Fourier Transform of the auto-correlation function of the aperture illumination, u( , ) National Radio Astronomy Observatory Sept 2005: Indiana University

Aperture-Beam Fourier Transform Relationship u ( , ) = aperture illumination |u ( )|2 = Electric field distribution across the aperture ( , ) = aperture coordinates ; u( , ) = far-field electric field |u ( )|2 ( , ) = direction relative to “optical axis” of telescope : :

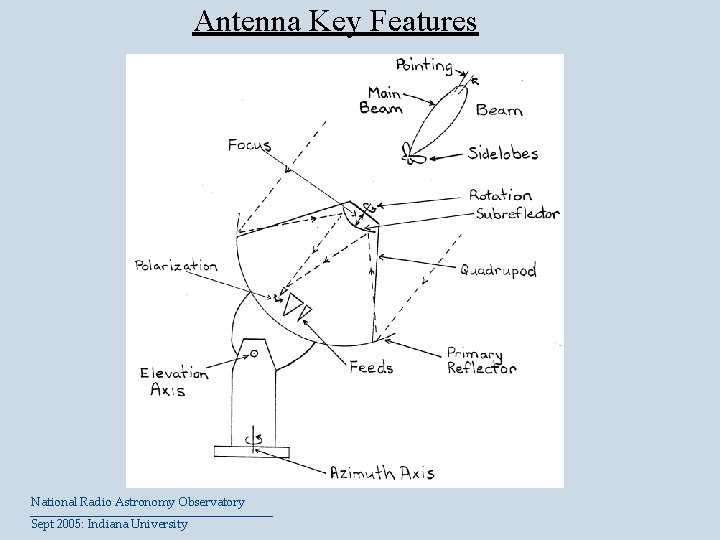
Antenna Key Features National Radio Astronomy Observatory Sept 2005: Indiana University

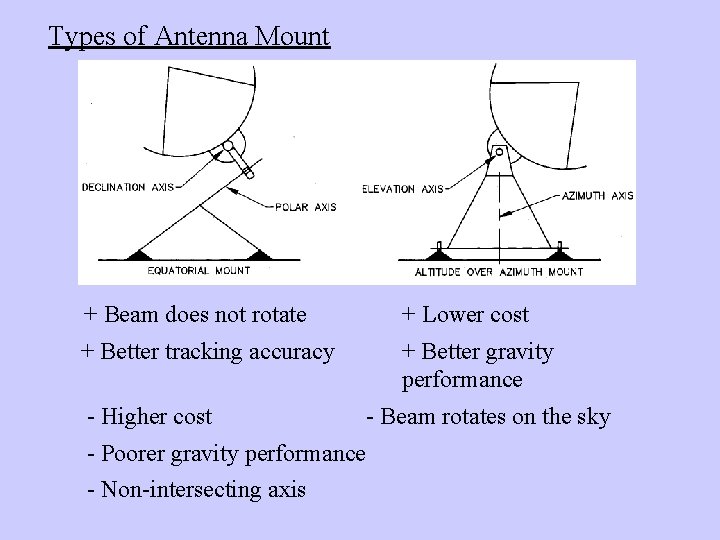
Types of Antenna Mount + Beam does not rotate + Lower cost + Better tracking accuracy + Better gravity performance - Higher cost - Poorer gravity performance - Non-intersecting axis - Beam rotates on the sky

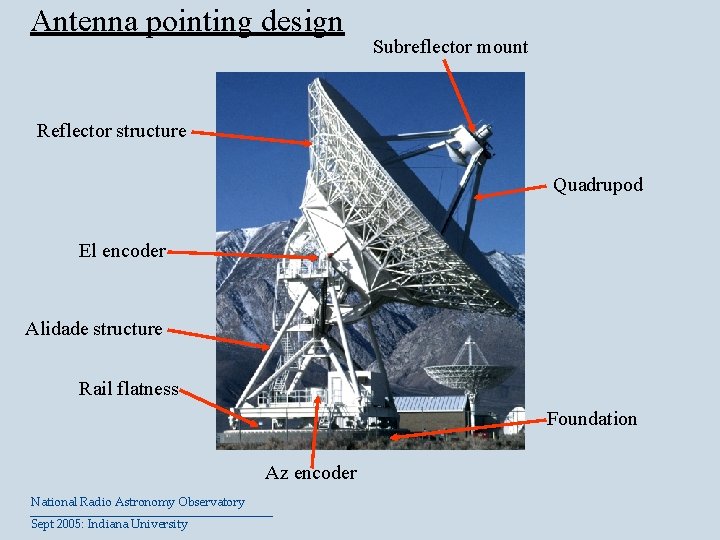
Antenna pointing design Subreflector mount Reflector structure Quadrupod El encoder Alidade structure Rail flatness Foundation Az encoder National Radio Astronomy Observatory Sept 2005: Indiana University

What happens to the signal collected by the antenna? Heterodyne Detection • At the focus, the radiation is collected by the receiver through a “feed” into a receiver that “pre-amplifies” the signal. • Then, the signal is mixed with a local oscillator signal close in frequency to the observing frequency in a nonlinear device (mixer). • The beat signal (IF or intermediate frequency signal) is usually amplified again before going through a bandwidth defining filter. (Frequency translation) • Then the IF signal is detected by a square-law detector. RF at fsky Pre-amplifier LO at f. LO IF at fsky f. LO Amplification and filtering Voltage |E|2

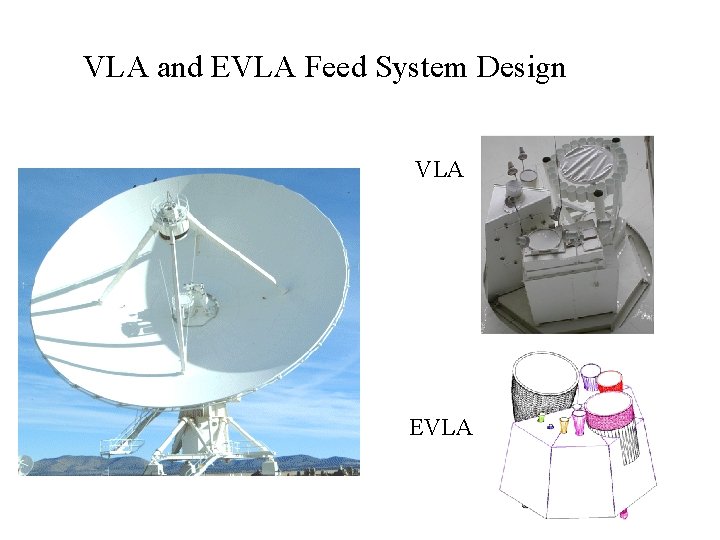
VLA and EVLA Feed System Design VLA EVLA

Wideband LBand OMT and Feed Horn National Radio Astronomy Observatory Sept 2005: Indiana University

Receivers in the telescope PF 1 -1: PF 1 -2: PF 1 -3: PF 1 -4: PF 2 : Gregorian Receiver Room L S C X Ku K 1 K 2 Q 0. 29 - 0. 40 GHz 0. 38 - 0. 52 0. 51 - 0. 69 0. 68 - 0. 92 0. 91 - 1. 23 : 1. 15 - 1. 73 GHz : 1. 73 - 2. 60 : 3. 95 - 5. 85 : 8. 00 - 10. 0 : 12. 0 - 15. 4 : 18. 0 - 22. 0 : 22. 0 - 26. 5 : 40. 0 - 52. 0

Radiometer Equation • For an unresolved source, the detection sensitivity of a radio telescope is determined by the effective area of the telescope and the “noisiness” of the receiver • For an unresolved source of a given flux, S , the expected antenna temperature is given by k. TA = ½ Ae, max. S • The minimum detectable TA is given by TA = Ts/ (B ) where Ts is the system temperature of the receiver, B is the bandwidth and is the integration time, and is of order unity depending on the details of the system. The system temperature measures the noise power of the receiver (Ps = Bk. Ts). In Radio Astronomy, detection is typically receiver noise dominated. National Radio Astronomy Observatory Sept 2005: Indiana University

High Resolution: Interferometry • Resolution /D – 5 cm/100 m = 2 arc-minute • Uses smaller telescopes to make much larger 'virtual' telescope • Maximum distance between antennas determines resolution • VLA = 22 -mile diameter radio telescope – 5 cm/22 miles = 0. 3 arc-second • Aperture Synthesis: Nobel Prize 1974 (Ryle) National Radio Astronomy Observatory Sept 2005: Indiana University D

VLA = Very Large Array (1980) Plain of San Augustine, New Mexico National Radio Astronomy Observatory Sept 2005: Indiana University 27 -antenna array: Extremely versatile Most productive telescope on ground

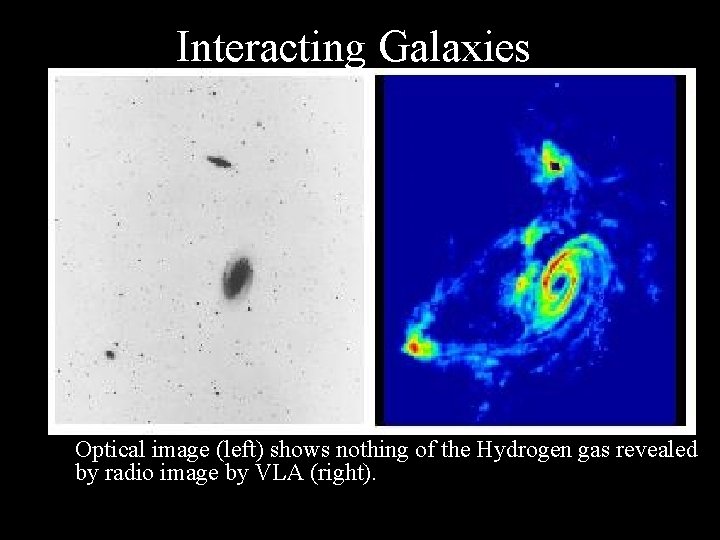
Interacting Galaxies • Optical image (left) shows nothing of the Hydrogen gas revealed by radio image by VLA (right).

Very Long Baseline Array • 10 25 m antennas • Continent-wide: 5400 mile diameter radio telescope • 6 cm/5400 miles = 0. 001 arc-second • Highest resolution imaging telescope in astronomy: 1 milli-arc-second = reading a news-paper at a distance of 2000 km National Radio Astronomy Observatory Sept 2005: Indiana University