How do EM Fields Propagate Transmission line equations









![Periodicity/Wavelength y = Asin[2 p(t/T – x/l)] Frequency f = 1/T Angular Frequency w=2 Periodicity/Wavelength y = Asin[2 p(t/T – x/l)] Frequency f = 1/T Angular Frequency w=2](https://slidetodoc.com/presentation_image_h/2f8a65bfd88995d10438d31894be15ce/image-21.jpg)

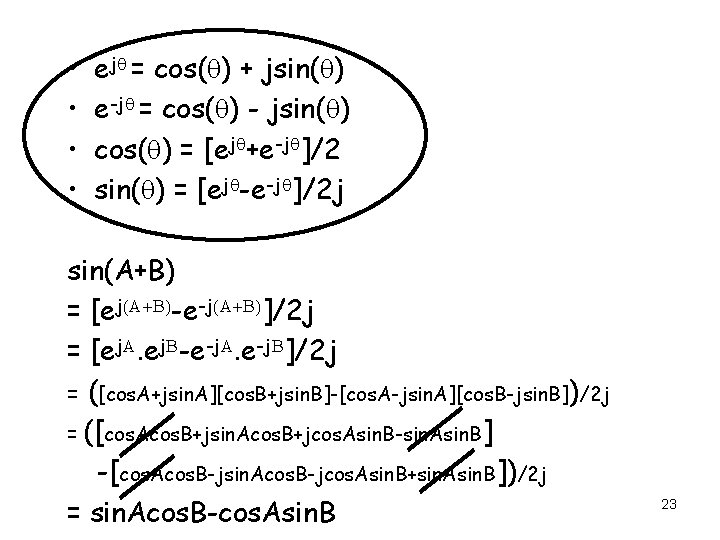



![R V 0 cos(wt) L ~ cos(wt) = Re[ejwt] sin(wt) = Im[ejwt] = Re[-jejwt] R V 0 cos(wt) L ~ cos(wt) = Re[ejwt] sin(wt) = Im[ejwt] = Re[-jejwt]](https://slidetodoc.com/presentation_image_h/2f8a65bfd88995d10438d31894be15ce/image-27.jpg)
- Slides: 28

How do EM Fields Propagate? • • • Transmission line equations Characteristic impedance of a line How much is reflected at a load? How would one eliminate this reflection? What about transient pulses? Transmission Line LOAD 1

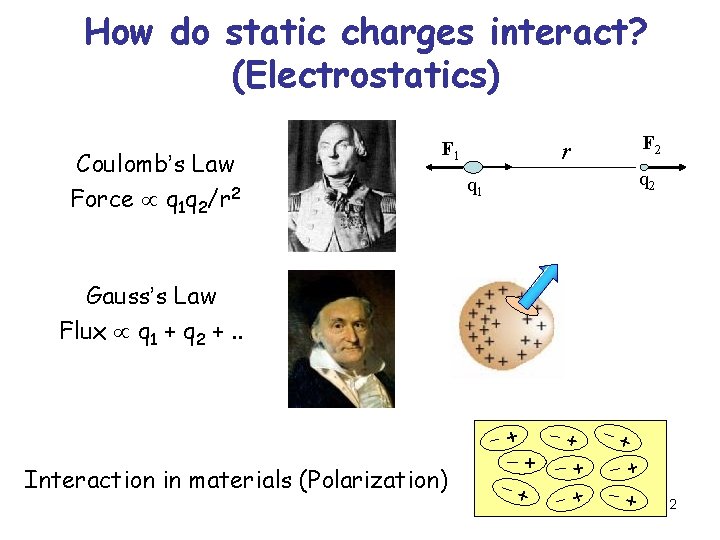
How do static charges interact? (Electrostatics) Coulomb’s Law Force q 1 q 2/r 2 F 1 F 2 r q 2 q 1 Gauss’s Law Flux q 1 + q 2 +. . + Interaction in materials (Polarization) + + + + 2

Vector Fields (A “disturbance in the force”) q E = lim F/q q 0 3

Vector Fields (A disturbance in the force) Non-negligible q 4

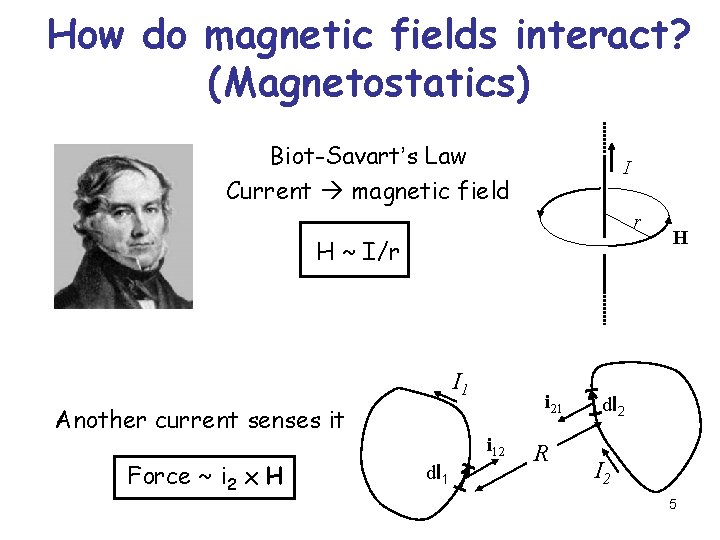
How do magnetic fields interact? (Magnetostatics) Biot-Savart’s Law Current magnetic field I r H ~ I/r I 1 Another current senses it Force ~ i 2 x H i 21 i 12 dl 1 R H dl 2 I 2 5

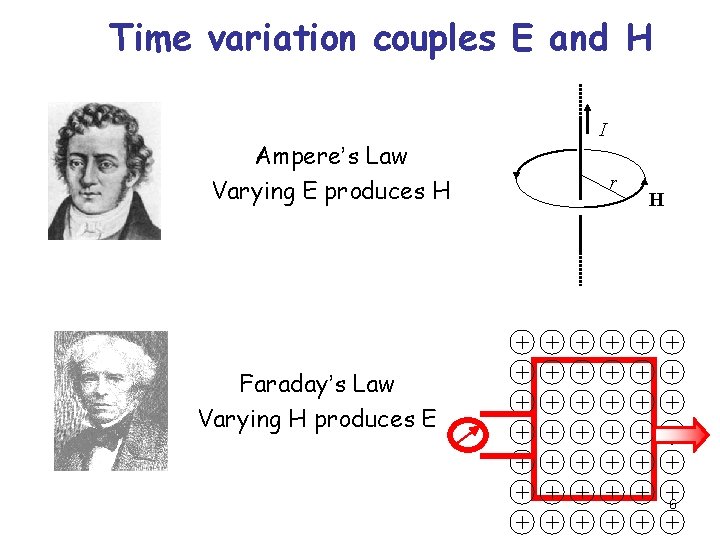
Time variation couples E and H Ampere’s Law Varying E produces H I r H Faraday’s Law Varying H produces E 6

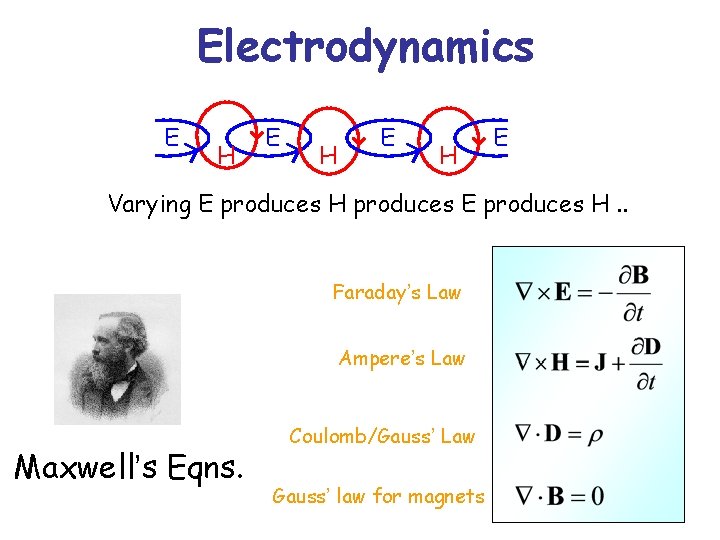
Electrodynamics E H E H E Varying E produces H produces E produces H. . Faraday’s Law Ampere’s Law Maxwell’s Eqns. Coulomb/Gauss’ Law Gauss’ law for magnets 7

Electrodynamics Don’t worry about memorizing these yet – We will come back to these later. But meanwhile, let’s try to understand them qualitatively. . Faraday’s Law Ampere’s Law Coulomb/Gauss’ Law Gauss’ law for magnets 8

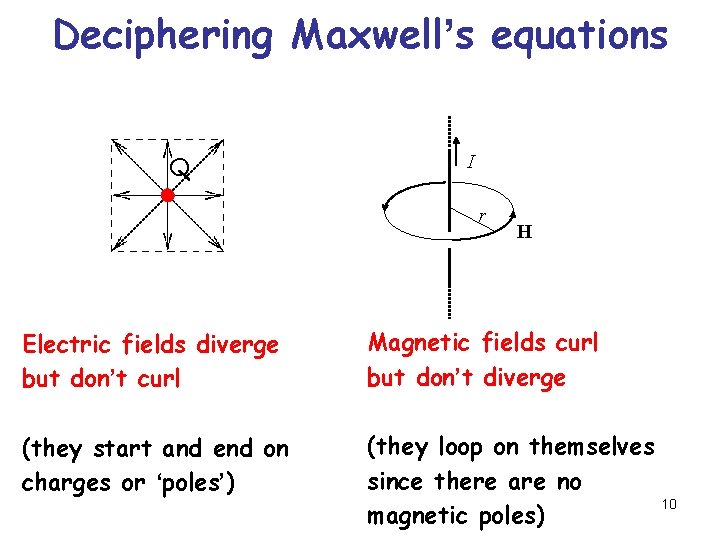
Deciphering Maxwell’s equations Q I r Electric fields diverge but don’t curl H Magnetic fields curl but don’t diverge 9

Deciphering Maxwell’s equations Q I r H Electric fields diverge but don’t curl Magnetic fields curl but don’t diverge (they start and end on charges or ‘poles’) (they loop on themselves since there are no 10 magnetic poles)

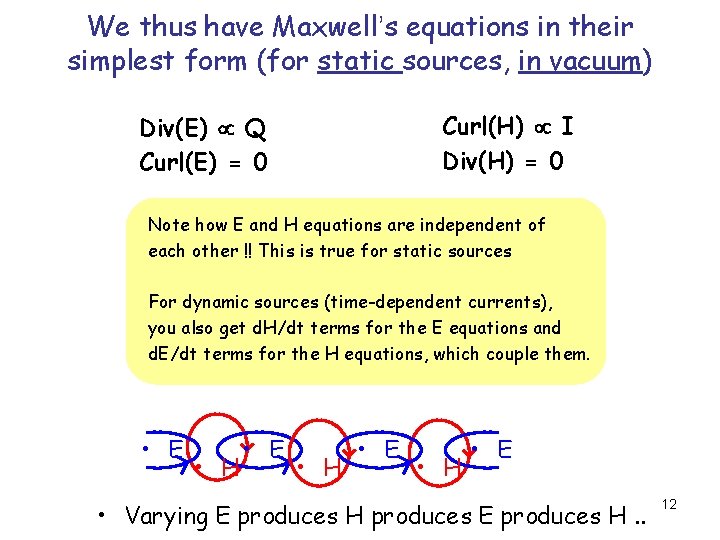
We thus have Maxwell’s equations in their simplest form (for static sources, in vacuum) Q I r Div(E) Q Curl(E) = 0 H Curl(H) I Div(H) = 0 We will define Div and Curl precisely later on. For now, think of them as the number of diverging and curling lines respectively 11

We thus have Maxwell’s equations in their simplest form (for static sources, in vacuum) Curl(H) I Div(H) = 0 Div(E) Q Curl(E) = 0 Note how E and H equations are independent of each other !! This is true for static sources For dynamic sources (time-dependent currents), you also get d. H/dt terms for the E equations and d. E/dt terms for the H equations, which couple them. • E • H • E • Varying E produces H produces E produces H. . 12

Consequences of Maxwell’s equations Waves Radiation 13

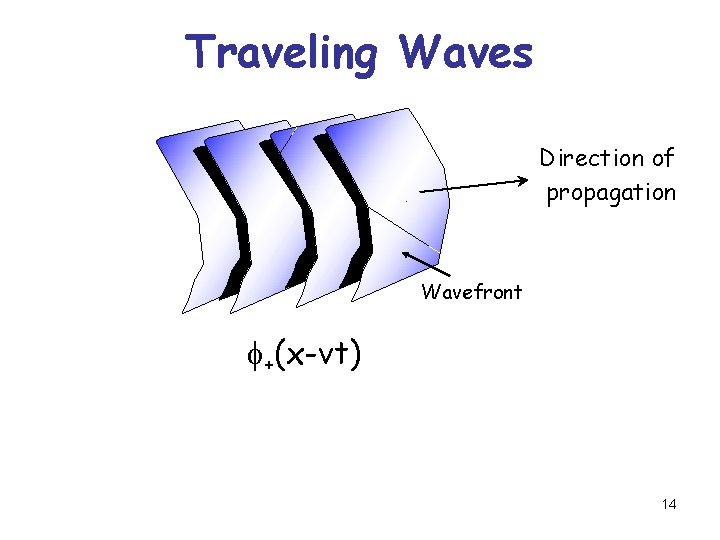
Traveling Waves Direction of propagation Wavefront f+(x-vt) 14

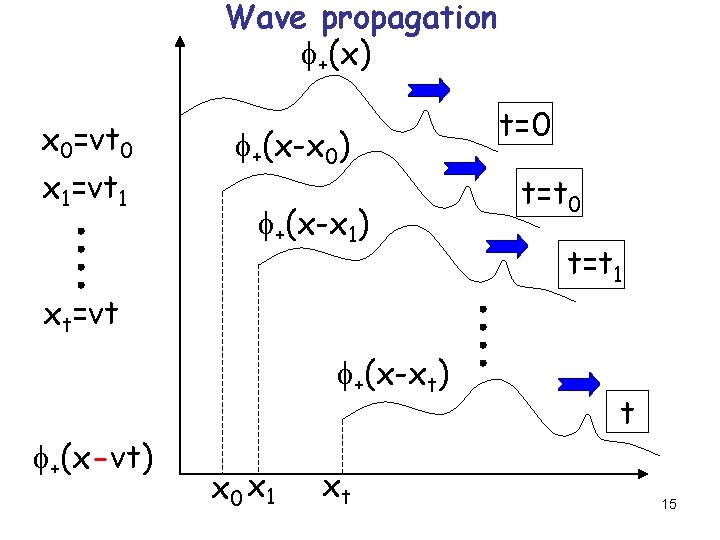
Wave propagation f+(x) x 0=vt 0 x 1=vt 1 f+(x-x 0) f+(x-x 1) t=0 t=t 1 xt=vt f+(x-xt) f+(x-vt) x 0 x 1 xt t 15

Sinusoid ASin(x-vt) For propagation direction, only relative sign between x and t matters 16

Sinusoid ASin(x+vt) For propagation direction, only relative sign between x and t matters 17

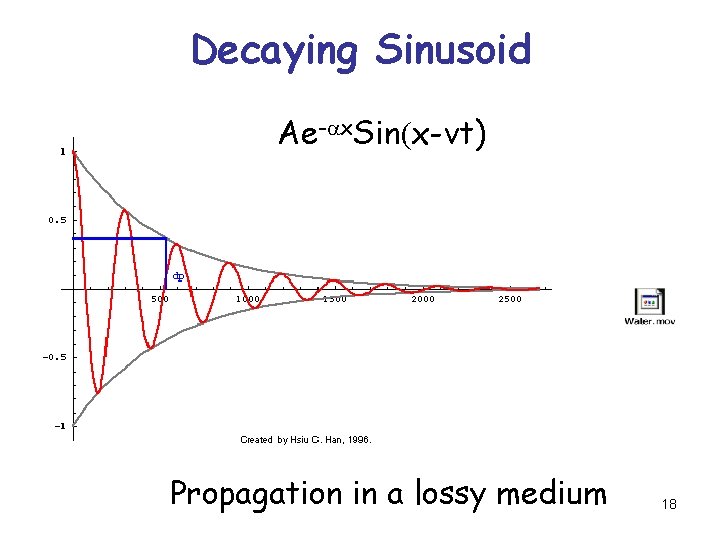
Decaying Sinusoid Ae-ax. Sin(x-vt) Propagation in a lossy medium 18

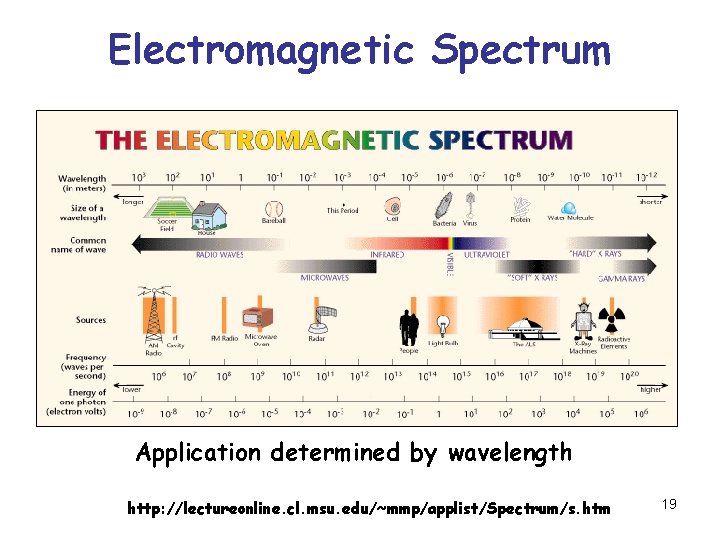
Electromagnetic Spectrum Application determined by wavelength http: //lectureonline. cl. msu. edu/~mmp/applist/Spectrum/s. htm 19

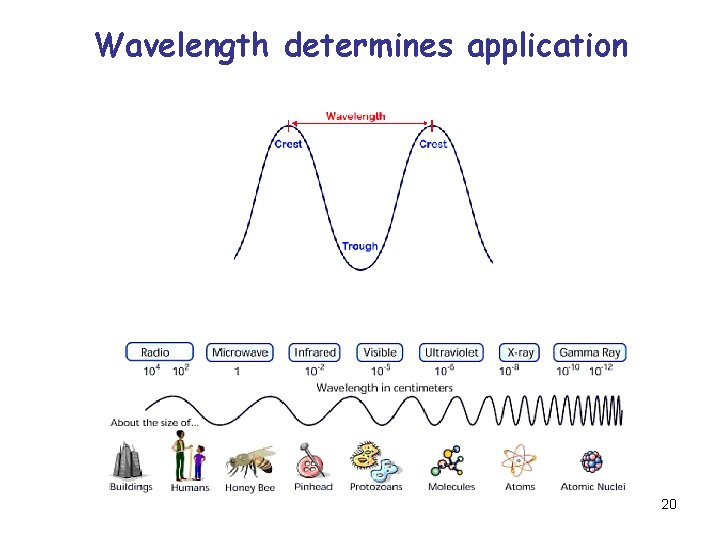
Wavelength determines application 20
![PeriodicityWavelength y Asin2 ptT xl Frequency f 1T Angular Frequency w2 Periodicity/Wavelength y = Asin[2 p(t/T – x/l)] Frequency f = 1/T Angular Frequency w=2](https://slidetodoc.com/presentation_image_h/2f8a65bfd88995d10438d31894be15ce/image-21.jpg)
Periodicity/Wavelength y = Asin[2 p(t/T – x/l)] Frequency f = 1/T Angular Frequency w=2 pf = 2 p/T y = Asin[2 pt/T] y = Asin[2 px/l] y = Asin[wt-bx] Wavenumber ~ n = 1/l Wavevector/Prop const b = 2 p/l 21

Complex #s, Phasors • ejq = cos(q) + jsin(q) Euler’s Formula • Profound!! Connects algebra with trig! • Converts PDEs into algebraic equations!! d/dq[ej(aq)] = a[ej(aq)] ∫dqej(aq) = ej(aq)/a • Trig identities become algebraic identities!! ejq 1. ejq 2 = ej(q 1+q 2) 22
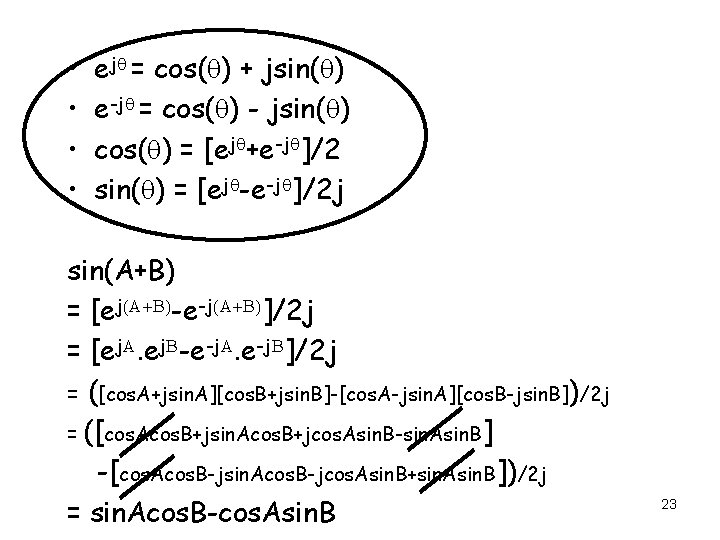
• • ejq = cos(q) + jsin(q) e-jq = cos(q) - jsin(q) cos(q) = [ejq+e-jq]/2 sin(q) = [ejq-e-jq]/2 j sin(A+B) = [ej(A+B)-e-j(A+B)]/2 j = [ej. A. ej. B-e-j. A. e-j. B]/2 j = ([cos. A+jsin. A][cos. B+jsin. B]-[cos. A-jsin. A][cos. B-jsin. B])/2 j = ([cos. Acos. B+jsin. Acos. B+jcos. Asin. B-sin. Asin. B] -[cos. Acos. B-jsin. Acos. B-jcos. Asin. B+sin. Asin. B])/2 j = sin. Acos. B-cos. Asin. B 23

Complex #s, Phasors • • ejq = cos(q) + jsin(q) z = |z|ejq = |z| q z* = |z|e-jq = |z| -q z 1 z 2 = (|z 1|ejq 1)(|z 2|ejq 2) = |z 1||z 2| (q 1 + q 2) • • zn = |z|n nq z 1/2 = |z|1/2 q/2 (q unknown upto 2 pm) z-1 = |z|-1 -q z 1/z 2 = (|z 1|ejq 1)/(|z 2|ejq 2) = |z 1|/|z 2| (q 1 - q 2) 24

Complex #s z = a + jb z* = a – jb Complex Conjugate zz* = a 2 + b 2 |z| = zz* = (a 2+b 2) Magnitude/Norm/Amplitude 1/z = z*/|z|2 = (a-jb)/(a 2+b 2) Rationalizing z=|z|ejq = |z|(cosq + jsinq) Phasor notation |z|cosq = a, |z|sinq = b Components |z| = (a 2+b 2), q = tan-1(b/a) 25

Phasor examples LC Phasor RLC Circuit 26
![R V 0 coswt L coswt Reejwt sinwt Imejwt Rejejwt R V 0 cos(wt) L ~ cos(wt) = Re[ejwt] sin(wt) = Im[ejwt] = Re[-jejwt]](https://slidetodoc.com/presentation_image_h/2f8a65bfd88995d10438d31894be15ce/image-27.jpg)
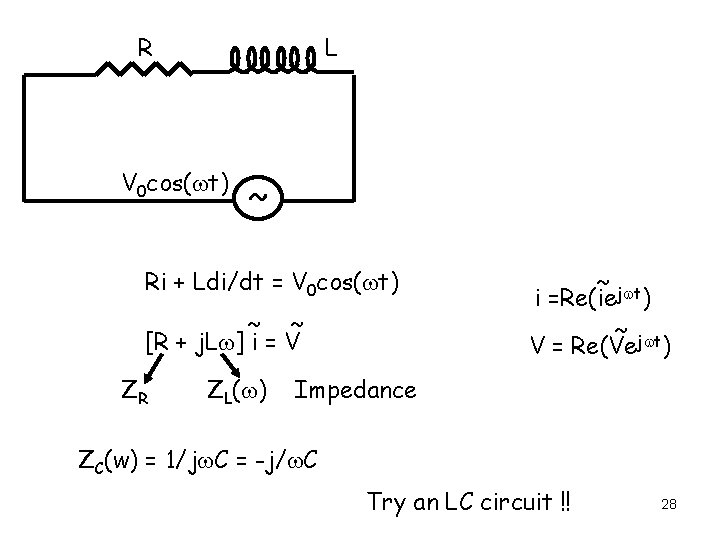
R V 0 cos(wt) L ~ cos(wt) = Re[ejwt] sin(wt) = Im[ejwt] = Re[-jejwt] j(wt-p/2)] = Re[e coswt+jsinwt Ri + Ldi/dt = V 0 cos(wt) ~ ~ [R + j. Lw] i = V ~ jwt i =Re(ie ) ~ jwt V = Re(Ve ) ~ ~ ~ i = V/[R+j. Lw] = V[R-j. Lw]/{R 2+L 2 w 2} i = Re(V 0 ejwt[R-j. Lw]/{R 2+L 2 w 2}) = V 0(Rcoswt+Lwsinwt)/{R 2+L 2 w 2} 27

R L V 0 cos(wt) ~ Ri + Ldi/dt = V 0 cos(wt) ~ ~ [R + j. Lw] i = V ZR ZL(w) ~ jwt i =Re(ie ) ~ jwt V = Re(Ve ) Impedance ZC(w) = 1/jw. C = -j/w. C Try an LC circuit !! 28