How Different are Quantitative and Qualitative Consequence Relations

How Different are Quantitative and Qualitative Consequence Relations for Uncertain Reasoning? David Makinson (joint work with Jim Hawthorne) 1

I Uncertain Reasoning 2

Consequence Relations • Many ways of studying uncertain reasoning • One way: consequence relations (operations) and their properties • Two approaches to their definition: – Quantitative (using probability) – Qualitative (various methods) • Tend to be studied by different communities 3

Behaviour Widely felt: quantitatively defined consequence relations rather less well-behaved than qualitative counterparts • But exactly how much do they differ, and in what respects? • Are there any respects in which the quantititive ones are more regular? 4

Tricks and Traps On quantitative side ØCan simulate qualitative constructions On qualitative side ØBehaviour varies considerably according to mode of generation 5

Policy • Don’t try to twist one kind of approach to imitate the other • Take most straightforward version of each • Compare their behaviour as they are 6

II Qualitative Side 7

Recall Main Qualitative Account • Name: preferential consequence relations • Due to: Kraus, Lehmann, Magidor • Status: Industry standard • Our presentation: With single formulae (rather than sets of them) on the left 8

Preferential models Structure S = (S, , | ) where: • S is an arbitrary set (elements called states) • is a transitive, irreflexive relation over S (called a preference relation) • | is a satisfaction relation between states and classical formulae (well-behaved on classical connectives ) 9

Preferential Consequence - Definition Given a preferential model S = (S, , | ), define consequence relation |~S by rule: a |~S x iff x is satisfied by every state s that is minimal among those satisfying a state : in S satisfied : under | minimal : wrt < 10

Example S = {s 1, s 2} s 1 s 2 : p, q, r p |~ r, but p q |~/ r Monotony fails Some other classical rules fail What remains? s 1 : p, q, r 11

KLM Family P of Rules a |~ a reflexivity When a |~ x and x | y then a |~ y RW: right weakening When a |~ x and a || b then b |~ x LCE: left classical equivalence When a |~ x y then a x |~ y VCM: very cautious monotony When a |~ x and b |~ x, then a b |~ x OR: disjunction in the premises When a |~ x and a |~ y, then a |~ x y AND: conjunction in conclusion 12

All Horn rules for |~ (with side-conditions) Whenever a 1 |~ x 1, …. , an |~ xn (premises with |~) and b 1 |- y 1, …. , bm |- ym (side conditions with |-) then c |~ z (conclusion) (No negative premises, no alternate conclusions; finitely many premises unless signalled) 13

KLM Representation Theorem A consequence relation |~ between classical propositional formulae is a preferential consequence relation (i. e. is generated by some stoppered preferential model) iff it satisfies the Horn rules listed in system P 14

III Quantitative Side 15

Ingredients and Definition • Fix a probability function p – Finitely additive, Kolgomorov postulates • Conditionalization as usual: pa(x) = p(a x)/p(a) – Fix a threshold t in interval [0, 1] • Define a consequence relation |~p, t , briefly |~, by the rule: a |~p, t x iff either pa(x) t or p(a) 0 16

Successes and Failures Succeed (zero and one premise rules of P) a |~ a Reflexivity When a |~ x and x | y then a |~ y RW: right weakening When a |~ x and a || b then b |~ x LCE: left classical equivalence When a |~ x y then a x |~ y VCM: very cautious monotony Fail (two-premise rules of P) When a |~ x and b |~ x, then a b |~ x OR: disjunction in premises When a |~ x and a |~ y, then a |~ x y AND: conjunction in conclusion 17

IV Closer Comparison 18

Two Directions Preferentially sound / Probabilistically sound – OR, AND – Look more closely later Probabilistically sound Preferentially sound ? – Nobody seems to have examined – Presumed positive 19

Yes and No Question Probabilistically sound Preferentially sound ? Answer Yes and No – depends on what kind of rule 20

Specifics Question – Prob. sound Pref. sound ? Answer Yes and No – depends on what kind of rule Specifics – Finite-premise Horn rules: Yes – Alternative-conclusion rules: No – Countable-premise Horn rules: No 21

Finite-Premise Horn rules Should have been shown c. 1990…Hawthorne & Makinson 2007 If the rule is probabilistically sound (i. e. holds for every consequence relation generated by a prob. function, threshold) then it is preferentially sound (i. e. holds for every consequence relation generated by a stoppered pref. model) 22

Alternate-Conclusion Rules Negation rationality (weaker than disjunctive rationality and rational monotony) When a |~ x, then a b |~ x or a b |~ x Well-known: – Probabilistically sound – Not preferentially sound - fails in some stoppered preferential models 23

Countable-Premise Horn Rules Archimedian rule (Hawthorne & Makinson 2007) Whenever a |~ ai (premises: i ) ai |~ xi (premises: i ) xi pairwise inconsistent (side conditions) then a |~ – – Probabilistically sound Archimedean property of reals: t 0 n: n. t 1 But not preferentially sound 24

Fails in this Preferential Model : r, qi (i ) Put a r ai q 1 … qi xi q 1 … qi qi n : r, q 1, . . , qn+1 2 : r, q 1, q 2, q 3, …. 1 : r, q 1, q 2, … (1) a |/~ (2) a |~ ai for all i (3) ai |~ xi for all i (4) xi pairwise inconsistent 25

Corollary • No representation theorem for probabilistic consequence relations in terms of finite-premise Horn rules • Contrast with KLM representation theorem for preferential consequence relations 26

Other Direction Pref. sound but not prob. sound: two-premise Horn rules: OR: When a |~ x and b |~ x, then a b |~ x AND: When a |~ x and a |~ y, then a |~ x y • Are there weakened versions that are prob. sound? • Can we get completeness over finite-premise Horn rules? – Representation no!, completeness maybe – Wedge between representation and completeness – Completeness relative to class of expressions 27

Weakened Versions of OR, AND XOR: When a |~ x, b |~ x and a | b then a b |~ x – Requires that the premises be exclusive – Well-known WAND: When a |~ x, a y |~ , then a |~ x y – Requires a stronger premise – Hawthorne 1996 28

Proposed Axiomatization for Probabilistic Consequence Hawthorne’s family O (1996): – The zero and one-premise rules of P – Plus XOR, WAND Open question: Is this complete for finite-premise Horn rules (possibly with side-conditions) ? Conjecture: Yes 29

Partial Completeness Results The following are equivalent for finite-premise Horn rules with pairwise inconsistent premise-antecedents (1) Prob. sound (2 a) Pref. sound (all stoppered pref. models) (2 b) Sound in all linear pref. models at most 2 states (3) Satisfies ‘truth-table test’ of Adams (4 a) Derivable from B {XOR} (when n 1, from B) (4 b) Derivable from family O (4 c) Derivable from family P for n 1: van Benthem 1984, Bochman 2001 Adams 1996 (claimed) 30

V No-Man’s Land between O and P 31

More about WAND: When a |~ x, a y |~ , then a |~ x y Secondition equivalent in O to each of: • a y |~ y • a y |~ z for all z • a b |~ y for all b (a |~ y ‘holds monotonically’) • (a y) b |~ y for all b 32

What Does a y |~ mean ? • Quantitatively: Either t = 0 or p(a y) = 0 • Qualitatively: Preferential model has no (minimal) a y states • Intuitively: a gives indefeasible support to y (certain but not logically certain) 33

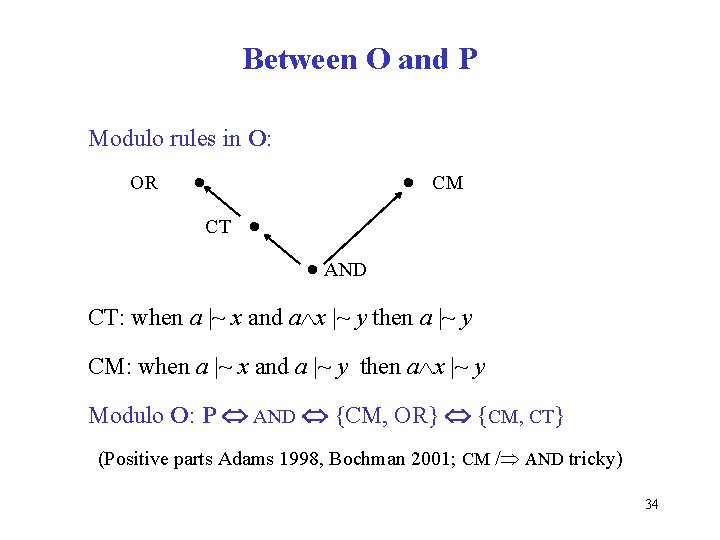
Between O and P Modulo rules in O: OR CM CT AND CT: when a |~ x and a x |~ y then a |~ y CM: when a |~ x and a |~ y then a x |~ y Modulo O: P AND {CM, OR} {CM, CT} (Positive parts Adams 1998, Bochman 2001; CM / AND tricky) 34

Moral • AND serves as a watershed condition between family O (sound for probabilistic consequence) and family P(characteristic for qualitative consequence) • No other single well-known rule does the same 35

VI Open Questions 36

Mathematical • Is Hawthorne’s family O complete for prob. consequence over finite-premise Horn rules ? Conjecture: positive • Can we give a representation theorem for prob. consequence in terms of O + NR + Archimedes + …? Conjecture: negative 37

Philosophical • Pref. consequence, as a formal modelling of qualitative uncertain consequence, validates AND • So do most others, e. g. Reiter default consequence • But do we really want that? – Perhaps it should fail even for qualitative consequence relations – Example: paradox of the preface 38

Paradox of the preface (Makinson 1965) An author of a book making a large number n of assertions may check and recheck them individually, and be confident of each that it is correct. But experience teaches that inevitably there will be errors somewhere among the n assertions, and the preface may acknowledge this. Yet these n+1 assertions are together inconsistent. – Inconsistent belief set, whether or not we accept AND – Inconsistent belief, if we accept AND 39

VII References 40

References James Hawthorne & David Makinson The quantitative/qualitative watershed for rules of uncertain inference Studia Logica Sept 2007 David Makinson Completeness Theorems, Representation Theorems: What’s the Difference? Hommage à Wlodek: Philosophical Papers decicated to Wlodek Rabinowicz, ed. Rønnow-Rasmussen et al. , www. fil. lu. se/hommageawlodek 41

VIII Appendices 42

What is Stoppering? To validate VCM: When a |~ x y then a x |~ y, we need to impose stoppering (alias smoothness) condition: Whenever state s satisfies formula a, either: • s is minimal under among the states satisfying a • or there is a state s s that is minimal under among the states satisfying a Automatically true in finite preferential models. Also true in infinite models when no infinite descending chains 43

Derivable from Family P Can derive SUP: supraclassicality: When a | x, then a |~ x CT: cumulative transitivity: When a |~ x and a x |~ y, then a |~ y Can’t derive Plain transitivity: When a |~ x and x |~ y, then a |~ y Monotony When a |~ x then a b |~ x 44

VCM versus CM KLM (1990) use CM: cautious monotony: When a |~ x and a |~ y, then a x |~ y instead of VCM When a |~ x y then a x |~ y These are equivalent in P (using AND and RW) But not equivalent in absence of AND 45

Kolmogorov Postulates Any function defined on the formulae of a language closed under the Boolean connectives, into the real numbers, such that: (K 1) 0 p(x) 1 (K 2) p(x) = 1 for some formula x (K 3) p(x) p(y) whenever x |- y (K 4) p(x y) = p(x) p(y) whenever x |- y 46

Conditionalization • Let p be a finitely additive probability function on classical formulae in standard sense (Kolmogorov postulates) • Let a be a formula with p(a) 0 • Write pa alias p( • |a) for the probability function defined by the standard equation pa(x) = p(a x)/p(a) • pa called the conditionalization of p on a 47

What is System B ? • Burgess 1981 • May be defined as the 1 -premise rules in O and P plus 1 -premise version of AND: VWAND: When a |~ x and a | y then a |~ x y • AND WAND VWAND 48

What is Adams’ Truth-Table Test ? There is some subset I {1, . . , n} such that both b y | i I(ai xi) and i I(ai xi) | b y – When n = 0 this reduces to: b | y – For n = 1, reduces to: either b | y or both a x | b y and a x | b y – Proof of 1 3 4 a in Adams 1996 has serious gap 49

Some Alternate-Conclusion Rules • Negation rationality when a |~ x then a b |~ x or a b |~ x • Disjunctive rationality when a b |~ x then a |~ x or b |~ x • Rational monotony when a |~ x then a b |~ x or a |~ b • Conditional Excluded Middle a |~ x or a |~ x Of these, NR alone holds for probabilistic consequence 50