HOW AIR AND WATER MOVE THINGS Bernoullis law

HOW AIR AND WATER MOVE THINGS Bernoulli’s law and Magnus force

Hydrostatic pressure Blaise Pascal P = ρgh

Hydrostatic pressure ρ=fluid/gas density g=acceleration due to gravity h=height P = ρgh • Pressure in liquid/gas is isotropic. It acts equally in all directions • Pressure is force per unit area • Due to the gravity, pressure at a given level equals to the weight of the column of liquid/gas above this level over a unit area

Pressure measurement: liquid (mercury) manometer

Hydrostatic pressure of air and water

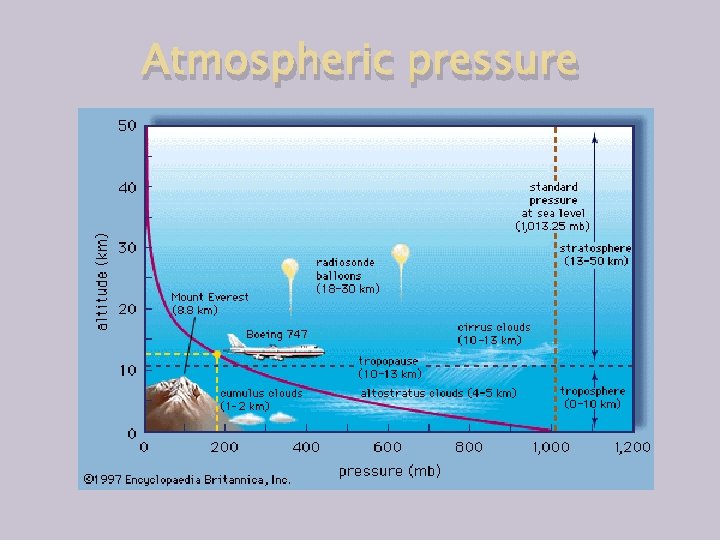
Atmospheric pressure

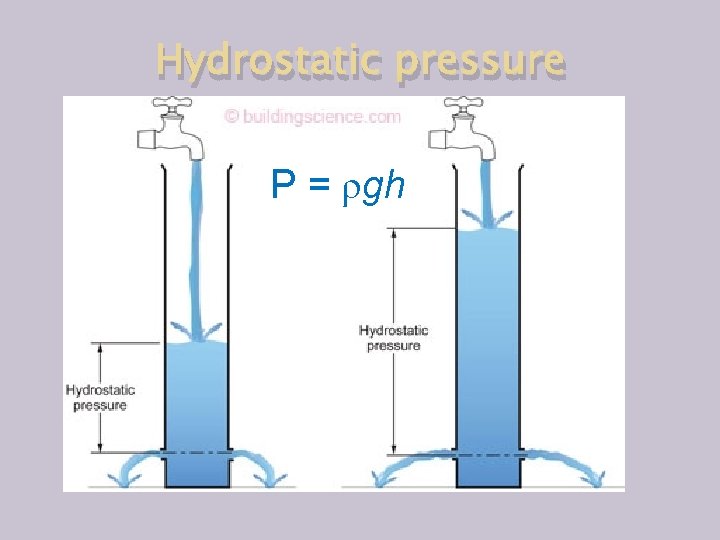
Hydrostatic pressure P = ρgh

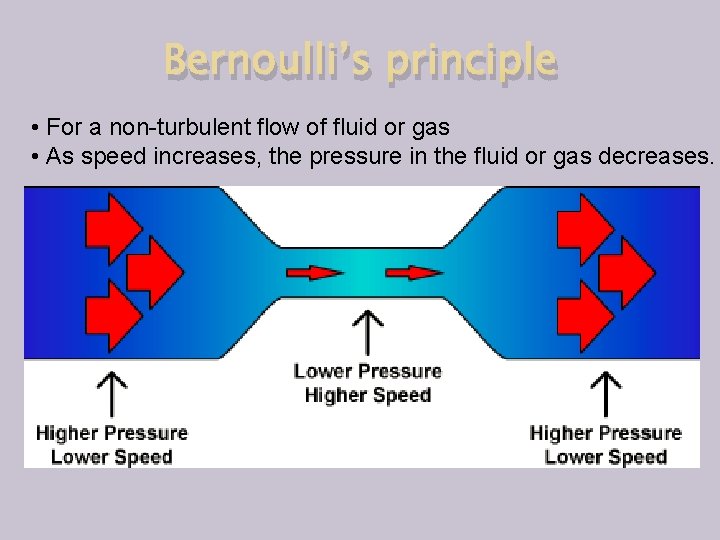
Bernoulli’s principle • For a non-turbulent flow of fluid or gas • As speed increases, the pressure in the fluid or gas decreases.

Bernoulli’s equation P + ½ ρv 2+ ρgh = const P=pressure of the fluid/gas along the streamline v=velocity of the fluid/gas along the streamline g=acceleration due to gravity h=height ρ=fluid/gas density The Bernoulli’s equation expresses conservation of enegy. It assumes that: The fluid/gas has a constant density The fluid/gas is traveling in a steady flow There is no friction The fluid/gas is non viscous and incompressable

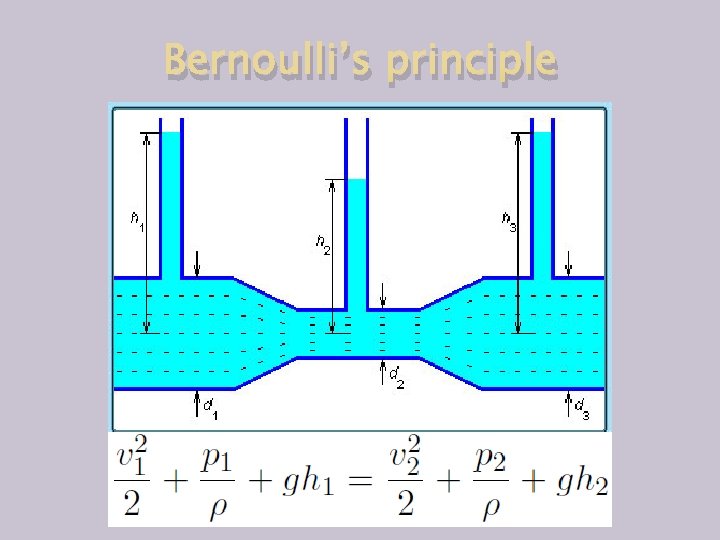
Bernoulli’s principle

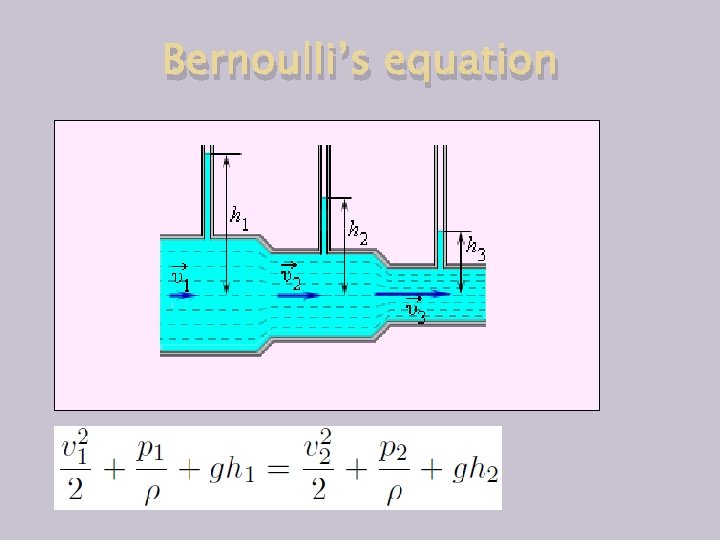
Bernoulli’s equation

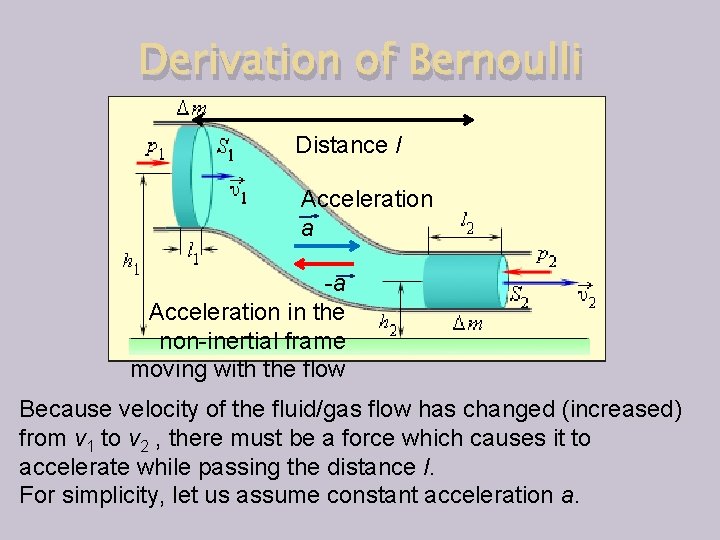
Derivation of Bernoulli Distance l Acceleration a -a Acceleration in the non-inertial frame moving with the flow Because velocity of the fluid/gas flow has changed (increased) from v 1 to v 2 , there must be a force which causes it to accelerate while passing the distance l. For simplicity, let us assume constant acceleration a.

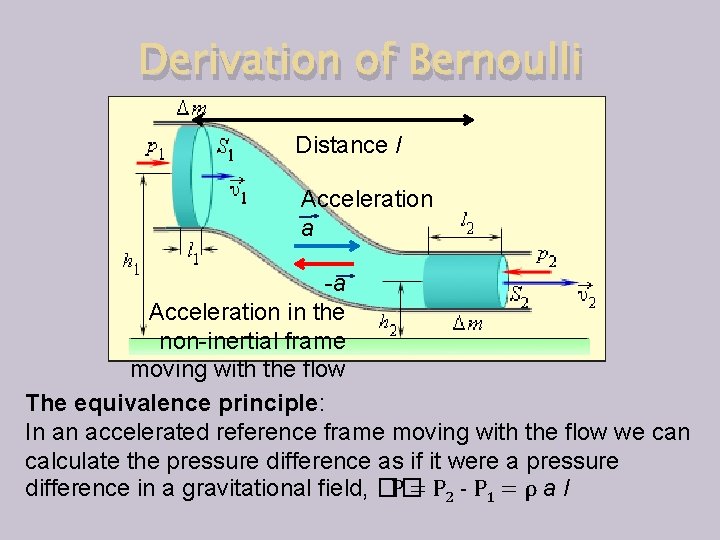
Derivation of Bernoulli Distance l Acceleration a -a Acceleration in the non-inertial frame moving with the flow The equivalence principle: In an accelerated reference frame moving with the flow we can calculate the pressure difference as if it were a pressure difference in a gravitational field, �� P = P 2 - P 1 = ρ a l

Inertial force and the equivalence principle

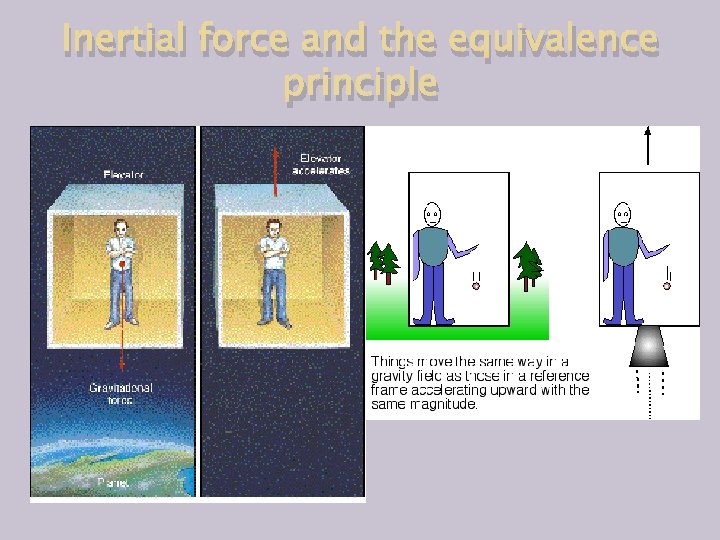
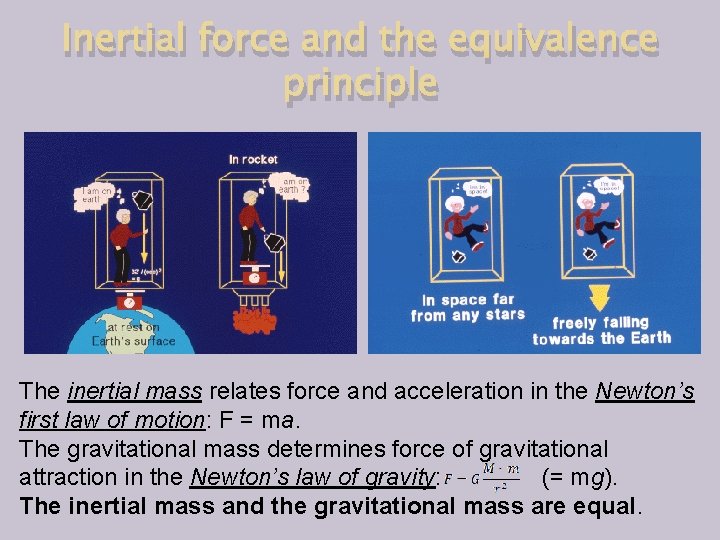
Inertial force and the equivalence principle The inertial mass relates force and acceleration in the Newton’s first law of motion: F = ma. The gravitational mass determines force of gravitational attraction in the Newton’s law of gravity: (= mg). The inertial mass and the gravitational mass are equal.

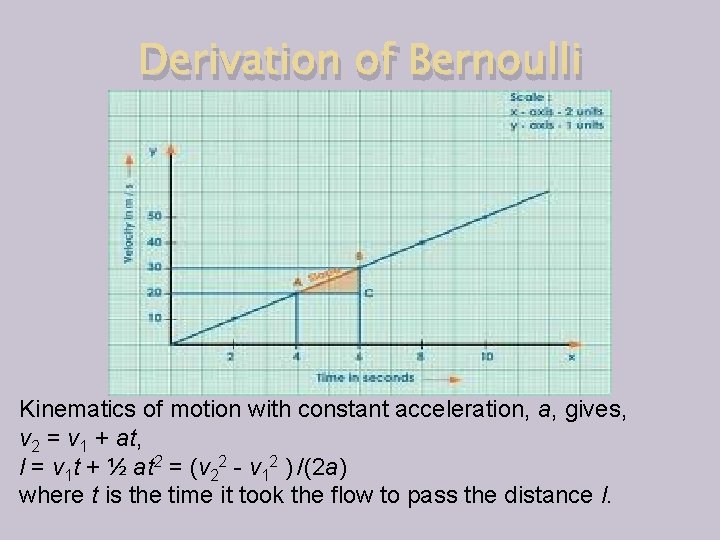
Derivation of Bernoulli Distance l Acceleration a -a Acceleration in the non-inertial frame moving with the flow Kinematics of motion with constant acceleration, a, gives, v 2 = v 1 + at, l = v 1 t + ½ at 2 = (v 22 - v 12 ) /(2 a) where t is the time it took the flow to pass the distance l.

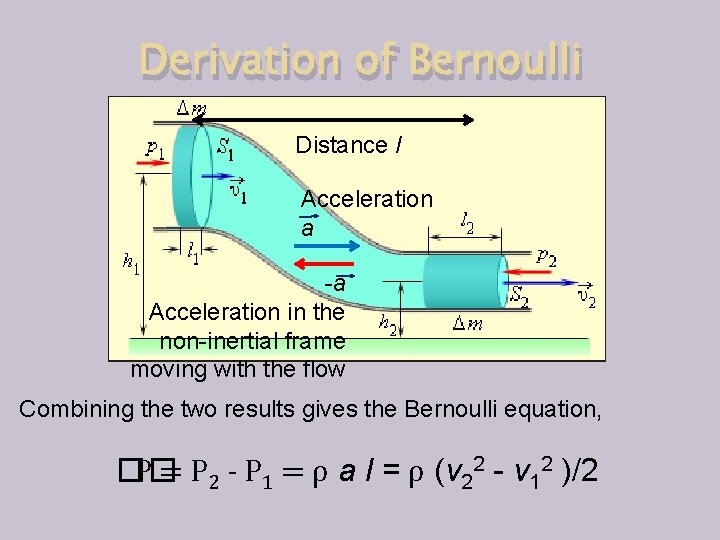
Derivation of Bernoulli Distance l Acceleration a -a Acceleration in the non-inertial frame moving with the flow Combining the two results gives the Bernoulli equation, �� P = P 2 - P 1 = ρ a l = ρ (v 22 - v 12 )/2

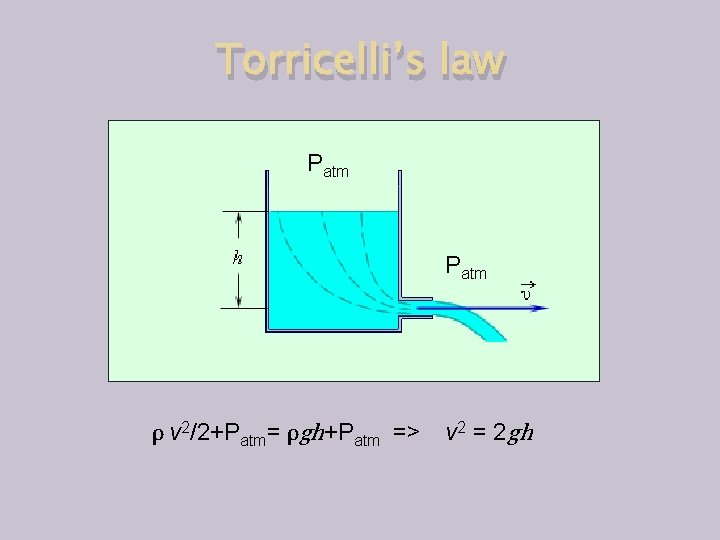
Torricelli’s law Patm ρ v 2/2+Patm= ρgh+Patm => v 2 = 2 gh

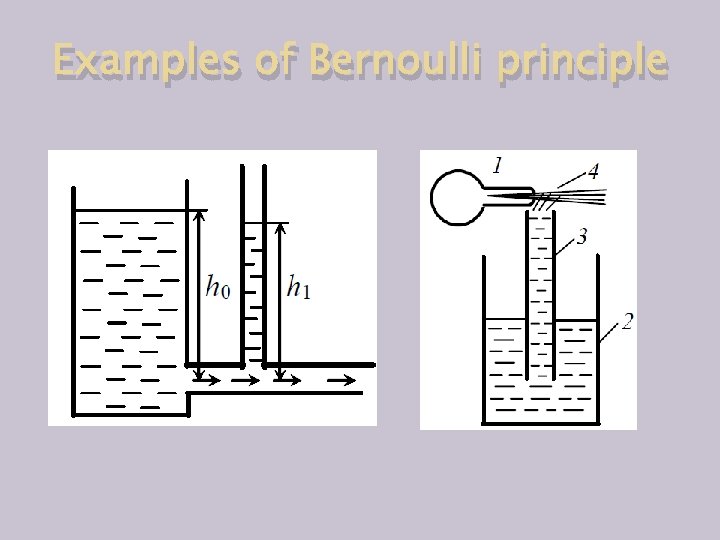
Examples of Bernoulli principle

Sprayers and atomizers

Ventouri effect and applications Ventouri detergent intake system in a powerwasher Ventouri wine aerator Dental Saliva Ejector Hose With Water Venturi Suction System

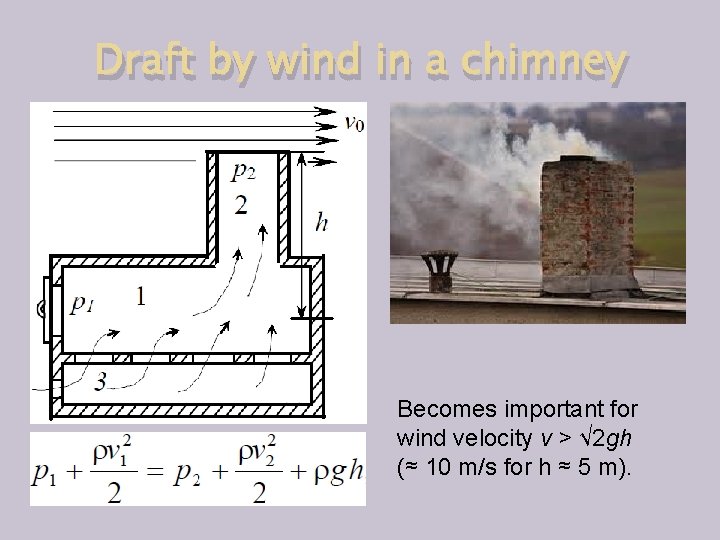
Draft by wind in a chimney Becomes important for wind velocity v > √ 2 gh (≈ 10 m/s for h ≈ 5 m).

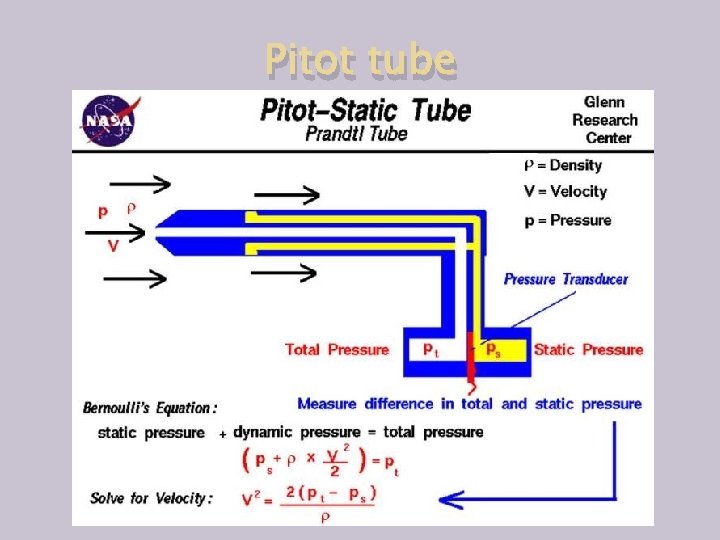
Pitot tube

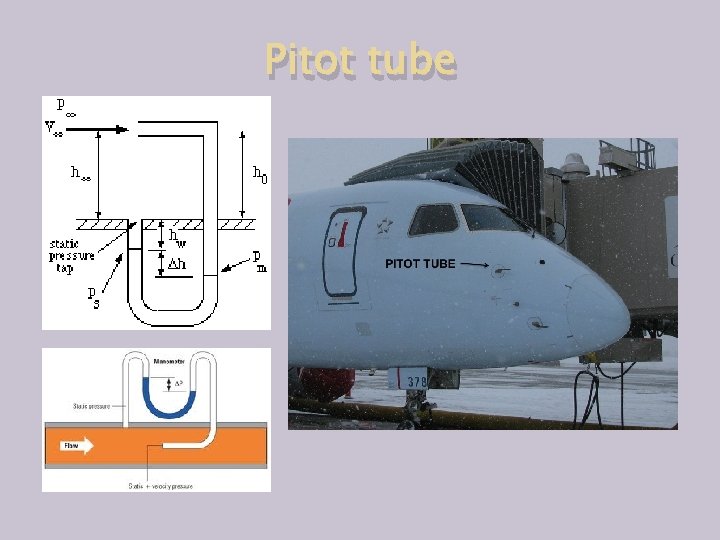
Pitot tubes

Spectacular effect Bernoulli

Ships passing on parallel course Ships sailing side by side can get too close together (as in picture above, at a certain point during the refueling). When this happens, the Venturi effect takes over, and the ships will head toward an unavoidable collision

Bernoulli pull by passing trains

An airfoil in a wind tunnel

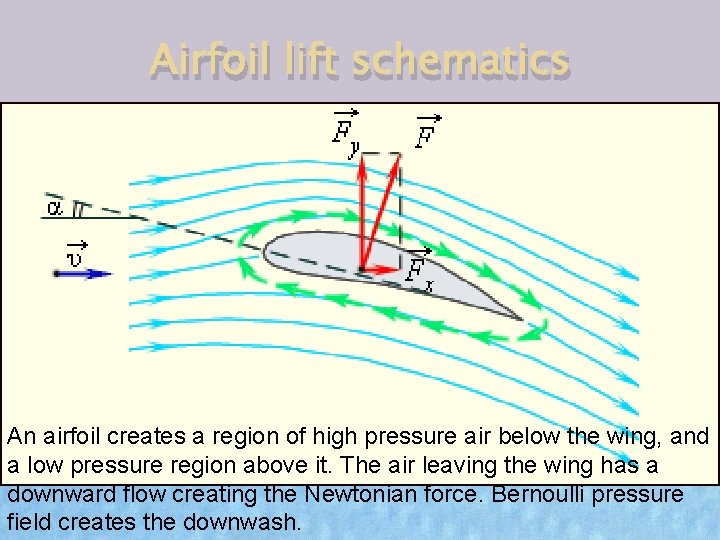
Airfoil lift schematics An airfoil creates a region of high pressure air below the wing, and a low pressure region above it. The air leaving the wing has a downward flow creating the Newtonian force. Bernoulli pressure field creates the downwash.

Flying machines

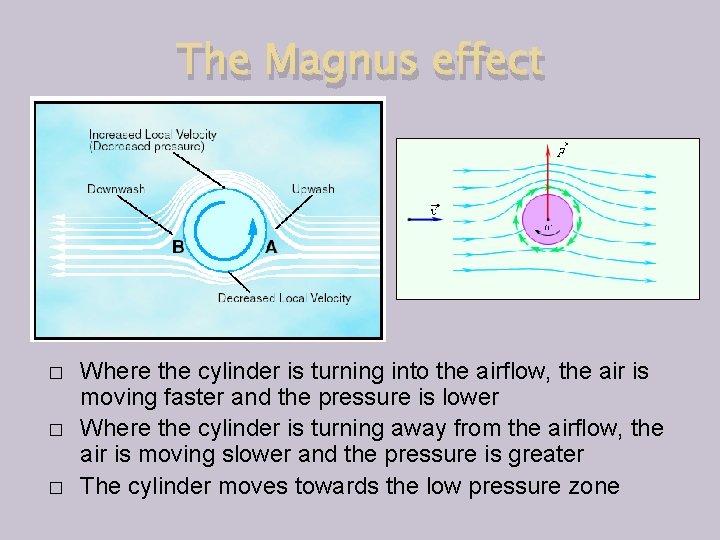
The Magnus effect � � � Where the cylinder is turning into the airflow, the air is moving faster and the pressure is lower Where the cylinder is turning away from the airflow, the air is moving slower and the pressure is greater The cylinder moves towards the low pressure zone

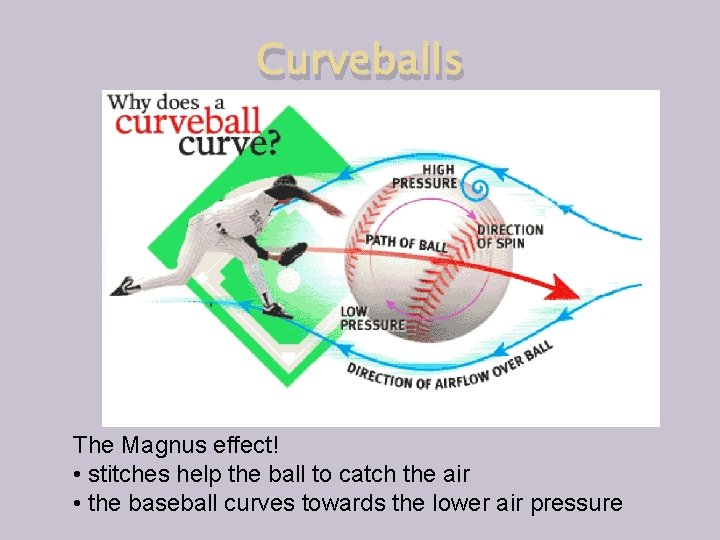
Curveballs The Magnus effect! • stitches help the ball to catch the air • the baseball curves towards the lower air pressure

Physics of golf: dimples on the ball and the Magnus effect Typical ball spin-rates are: 3, 600 rpm when hit with a 10 ° driver (8 ° launch angle) at a velocity of 134 mph 7, 200 rpm when hit with a 5 iron (23 ° launch angle) at a velocity of 105 mph 10, 800 rpm when hit with a 9 iron (45 ° launch angle) at a velocity of 90 mph Dimples cause the air-flow above the ball to travel faster and thus the pressure on the ball from the top to be lower than the air pressure below the ball. This pressure difference (i. e. more relative pressure from below than on top) causes the ball to lift (Magnus effect) and stay in the air for a longer time. Topping the ball (i. e. when the bottom of the club-face hits the ball above its center) will cause the ball to spin in the other direction i. e. downward - which will cause the ball to dive into the ground.

Flettner rotor ship Buckau (Baden) 1927

Flettner rotor ship E-1 (Kiel 2010)

Flettner rotor sail catamaran